Entwicklung der Zahlenmengen

R. Brinkmann http://brinkmann-du.de
Seite 1
05.10.2008
Entwicklung der Zahlenmengen
In der Mathematik werden die Rechenoperationen mit Hilfe von Zahlen definiert.
Durch die Entwicklung der Rechenarten von der Addition bis hin zum Logarithmieren
wurde die Unzulänglichkeit der Zahlenmenge offenbar, mit der gerade operiert
wurde.
So bestand der zuerst bekannte Zahlenbereich aus Zahlen, die zum Abzählen
benötigt wurden, also die positiven ganzen Zahlen, die als natürliche Zahlen
bezeichnet werden.
In der Mengenlehre sind die Zahlen als Elemente von Zahlenmengen festgelegt, in
den sogenannten Standardmengen.
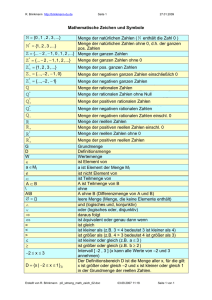
Menge der natürlichen
Zahlen.
Definition
Symbol: `
` = {0 ; 1; 2 ; 3 ; 4 ;...}
0∈`
Die Menge der natürlichen Zahlen `
enthält die Zahlen, die zum Abzählen benötigt werden
einschließlich der Zahl Null.
Die Definition ordnet das Element 0 der Menge der natürlichen Zahlen zu. Obwohl
dies vom Begriff des Abzählens nicht direkt einzusehen ist, wird dadurch jedoch die
Symbolik der Zahlengrundmengen vereinfacht. Aber auch die Schreibweise von
Indizes an Koeffizienten beginnt meist mit 0.
a0 + a1x + a2 x 2 + ... + an x n
n∈`
Innerhalb der natürlichen Zahlen ist die Verknüpfung Addition abgeschlossen, d. h.
die Addition zweier natürlicher Zahlen führt wieder zu einer natürlichen Zahl.
2 + 5 = 7
a+b =c
a, b, c ∈ `
Die Subtraktion ist nicht abgeschlossen, da nicht jede dieser Verknüpfungen wieder
zu einem Element aus IN führt.
5 − 8 = −3
−3∉`
Die Zahlenmenge muss also so erweitert werden, dass die Verknüpfung Subtraktion
uneingeschränkt möglich ist. Diese Zahlenmenge ist die Menge der ganzen Zahlen.
Definition
Die Menge der ganzen Zahlen enthält die Elemente der Menge der
natürlichen Zahlen und alle negativen ganzen Zahlen.
Menge der ganzen Zahlen.
Symbol: ]
] = {.....; − 2 ; − 1; 0 ; 1; 2 ; 3 ; 4 ;...}
In der Menge der ganzen Zahlen sind die Verknüpfungen Addition, Subtraktion und
Multiplikation abgeschlossen. Bei der Division zeigt sich jedoch wieder die
Unzulänglichkeit dieser Zahlenmenge.
Erstellt von R. Brinkmann p0_zahlenmengen_01.doc
03.09.2007 11:20
Seite 1 von 3
R. Brinkmann http://brinkmann-du.de
Seite 2
05.10.2008
6
∉]
7
Die Erweiterung der Menge der ganzen Zahlen um die Bruchzahlen führt zur Menge
der rationalen Zahlen, in der die Division nahezu uneingeschränkt möglich ist.
Die Division durch Null ist nicht erlaubt.
Definition Die Menge der rationalen Zahlen ist die Menge aller Zahlen q, für die gilt:
6:7 =
m
n
und m ist Element der Menge ]
und n ist Element der Menge ] ohne Null.
m
Symbol: _ = {q | q = ∧ m ∈ ] ∧ n ∈ ] * }
n
q=
Nach DIN 5473 werden die Standardmengen mit einem Stern gekennzeichnet,
wenn das Element 0 nicht enthalten sein soll, also ` * , ] * , _* , \ *
Für jede rationale Zahl gibt es unendlich viele Schreibweisen, so dass in der
aufzählenden Form der Menge nur die Repräsentanten (nicht mehr kürzbare Brüche)
aufgeführt werden.
1 2 4 6
64
= = = = .... =
= ...
2 4 8 3
128
Zusätzlich zu den rationalen Zahlen existieren auf dem Zahlenstrahl Punkte,
die keiner rationalen Zahl entsprechen, also nicht durch
m
q=
mit m ∈ ] und n ∈ ] *
n
dargestellt werden können.
2 ∉ _ π ∉ _ sin(480 ) ∉ _ lg 2 ∉ _
Da diesen Zahlen wie den rationalen Zahlen wirklich ein Punkt auf dem Zahlenstrahl
zugeordnet ist, nennt man alle Zahlen, denen genau ein Punkt auf dem Zahlenstrahl
zugeordnet ist, die Menge der reellen Zahlen.
Definition Die Menge der reellen Zahlen ist die Menge aller Punkte des Zahlenstrahls.
Symbol: \
2
2
-5 -4 -3 -2 -1
0
1
2
3
4
5
In der Menge der reellen Zahlen sind die Verknüpfungen Addition, Subtraktion
Multiplikation, Potenzieren, uneingeschränkt und die Division ohne Divisor 0 möglich.
Erstellt von R. Brinkmann p0_zahlenmengen_01.doc
03.09.2007 11:20
Seite 2 von 3
R. Brinkmann http://brinkmann-du.de
Seite 3
05.10.2008
−45 ∉ \ log2 ( −8) ∉ \
Die Verknüpfungen Radizieren und Logarithmieren sind nicht uneingeschränkt
möglich.
Diese Verknüpfungen sind in einer nochmals erweiterten Zahlenmenge
abgeschlossen, der Menge der komplexen Zahlen.
Erstellt von R. Brinkmann p0_zahlenmengen_01.doc
03.09.2007 11:20
Seite 3 von 3