1. Rechnen mit Vektoren
Werbung
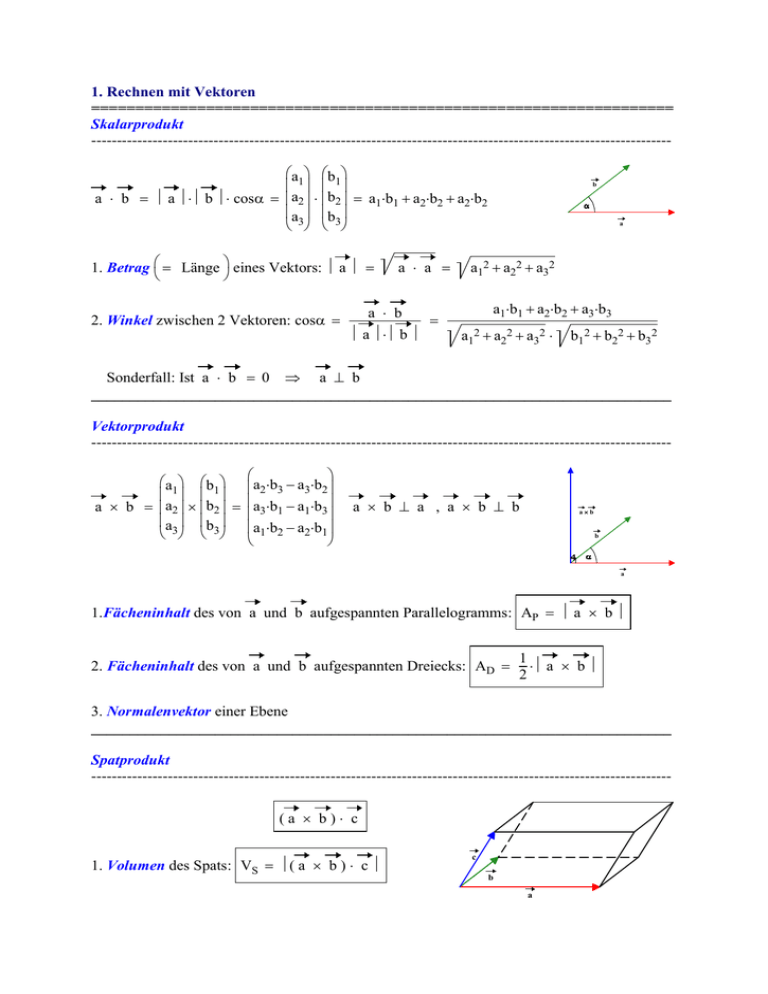
1. Rechnen mit Vektoren ================================================================== Skalarprodukt -----------------------------------------------------------------------------------------------------------------a1 b1 a b a b cos a2 b2 a1b1 a2b2 a2b2 a b 3 3 1. Betrag Länge eines Vektors: a a a a b 2. Winkel zwischen 2 Vektoren: cos a b b a a12 a22 a32 a1b1 a2b2 a3b3 a12 a22 a32 b1 2 b 2 2 b 3 2 Sonderfall: Ist a b 0 a b ___________________________________________________________________________ Vektorprodukt -----------------------------------------------------------------------------------------------------------------a1 b1 a2b3 a3b2 a b a2 b2 a3b1 a1b3 a b a b a b 3 3 1 2 2 1 a b a , a b b ab b a 1.Fächeninhalt des von a und b aufgespannten Parallelogramms: AP a b 2. Fächeninhalt des von a und b aufgespannten Dreiecks: AD 1 a b 2 3. Normalenvektor einer Ebene ___________________________________________________________________________ Spatprodukt -----------------------------------------------------------------------------------------------------------------(a b) c 1. Volumen des Spats: VS ( a b ) c c b a 2. Rauminhalt des Tetraeders: VT 1 ( a b ) c 6 c b a 3. ( a b ) c 0 a , b und c sind voneinander linear abhängig ___________________________________________________________________________ 2. Vektoren und Punkte ================================================================== Ortsvektor -----------------------------------------------------------------------------------------------------------------a1 Punkt: Aa1 a2 a3 Ortsvektor: A OA a2 a A 3 ___________________________________________________________________________ Verbindungsvektor zwischen zwei Punkten ----------------------------------------------------------------------------------------------------------------- b1 a1 AB B A Verbindungsvektor zweier Punkte: AB B A b2 a2 A b3 a3 B ___________________________________________________________________________ Länge einer Strecke oder Abstand zweier Punkte ----------------------------------------------------------------------------------------------------------------- b1 a1 AB AB B A b2 a2 (b1 a1)2 (b2 a2)2 (b3 a3)2 b a 3 3 ___________________________________________________________________________ Winkel im Dreieck -----------------------------------------------------------------------------------------------------------------cos AB AC AB AC cos BA BC cos BA BC CA CB A C CA CB B ___________________________________________________________________________ Mittelpunkt einer Strecke ------------------------------------------------------------------------------------------------------------------ M 1 A B 2 A M B ___________________________________________________________________________ 3. Geraden ================================================================== Parametergleichung einer Geraden -----------------------------------------------------------------------------------------------------------------a1 v1 v g : X A v a2 v2 X a v A 3 3 ___________________________________________________________________________ Zeichnerische Darstellung - Spurpunkte -----------------------------------------------------------------------------------------------------------------Ein Schnittpunkt einer Geraden mit einer Koordinatenebene heißt Spurpunkt in dieser Ebene. Spurpunkt in der x1x2-Koordinatenebene Bedingung x3 0 x1x3-Koordinatenebene x2 0 x2x3-Koordinatenebene x1 0 Existiert kein Spurpunkt in einer Korordinatenebene, dann ist die Gerade zu dieser Koordinatenebene parallel. x3 x2 x1 -----------------------------------------------------------------------------------------------------------------Zweipunkteform -----------------------------------------------------------------------------------------------------------------AB : X A ( B A ) v AB B A B A __________________________________________________________________________ Parallele, sich schneidende und windschiefe Geraden -----------------------------------------------------------------------------------------------------------------g : X A v v k u h : g : X B u ghh Ist zusätzlich A h, dann sind g und h identisch. Ansonsten gilt die Schnittpunktsbedingung A v B u . Ist das sich ergebende Gleichungssystem nicht lösbar, dann sind g und h windschief. __________________________________________________________________________ 4. Ebenen ================================================================== Parametergleichung einer Ebene -----------------------------------------------------------------------------------------------------------------a1 u1 v1 v a u v E : X A u v 2 2 2 u a u v 3 3 3 A X ___________________________________________________________________________ Normalenform einer Ebenengleichung -----------------------------------------------------------------------------------------------------------------n X A n X A Normalenform: n X A 0 n1x1 n2x2 n3x3 ( n1a1 n2a2 n3a3) 0 n4 ___________________________________________________________________________ Zeichnerische Darstellung - Schnittpunkte mit den Koordinatenachsen - Spurgeraden -----------------------------------------------------------------------------------------------------------------Schnittpunkt mit der x1-Achse Bedingung x 2 x3 0 x2-Achse x 2 x3 0 x3-Achse x 2 x3 0 Existiert kein Schnittpunkt mit einer Koordinatenachse, dann ist die Ebene zu dieser Koordinatenachse parallel. Hat die Ebene mit einer Koordinatenachse mehr als einen Punkt gemeinsam, dann verläuft sie durch diese Achse. Die Schnittgeraden mit den Koordinatenebenen heißen Spurgeraden. Spurgerade in der x1x2-Koordinatenebene Bedingung x3 0 x1x3-Koordinatenebene x2 0 x2x3-Koordinatenebene x1 0 x3 x2 x1 __________________________________________________________________________ Lagebeziehung zwischen Ebenen und Geraden ----------------------------------------------------------------------------------------------------------------- g : X A v und E : n X A 0 ghE v n 0 Die Gerade g liegt in der Ebene, wenn zusätzlich ihr Aufpunkt A in E liegt. Ansonsten erhält man den zum Schnittpunkt gehörenden Parmeter durch Einsetzen des allgemeinen Geradenpunkts in eine Normalenform von E. Sonderfall: v gE v k n ___________________________________________________________________________ Lagebeziehung zwischen Ebenen -----------------------------------------------------------------------------------------------------------------Zwei Ebenen E und F mit den Normalenformen E : n1x1 n2x2 n3x3 n4 0 und F : m1x1 m2x2 m3x3 m4 0 n1 m1 sind parallel, wenn die Normalenvektoren n n2 und m m2 linear abhängig sind. n m 3 3 n1 m1 Das heißt, es gibt ein k R, so dass n2 km2 ist. n m 3 3 Gilt zusätzlich n4 km4, dann sind die Ebenen identisch. Ansonsten schneiden sich die beiden Ebenen in einer Geraden. Die parametrisierte Lösung des Gleichungssystems n x n x n x n 0 (1) 1 1 2 2 3 3 4 ist der allgemeine Geradenpunkt der Schnittgeraden s. (2) m1x1 m2x2 m3x3 m4 0 ___________________________________________________________________________ Hessesche Normalenform -----------------------------------------------------------------------------------------------------------------n 1 x 1 n 2 x 2 n3 x 3 n4 0 n1 2 n2 2 n 3 2 Setzt man die Koordinaten eines Punktes P in die HNF einer Ebene ein, dann erhält man eine Zahl, deren Betrag gleich dem Abstand des Punktes von der Ebene ist. Diese Zahl ist positiv, wenn der Punkt auf der dem Ursprung abgewandten Seite von E ist. Ist sie negativ, dann liegt P auf der Ursprungsseite. ___________________________________________________________________________ 5. Kugel ================================================================== X M M X 2 2 2 X M r (x1 m1)2 (x2 m2)2 (x3 m3)2 r ___________________________________________________________________________ MX r 6. Abstände ================================================================== Abstand eines Punktes von einer Geraden ------------------------------------------------------------------------------------------------------------------ d(P; g) PF v n ___________________________________________________________________________ Abstand eines Punktes von einer Ebene -----------------------------------------------------------------------------------------------------------------d(P; E) PF v n ___________________________________________________________________________ Abstand paralleler Geraden -----------------------------------------------------------------------------------------------------------------d(g; h) d(A; h) mit A g ___________________________________________________________________________ Abstand einer Geraden zu einer parallelen Ebene -----------------------------------------------------------------------------------------------------------------d(g;E) d(A; E) mit A g ___________________________________________________________________________ 7. Winkel ================================================================= Schnittwinkel sich schneidender bzw. Kreuzungswinkel windschiefer Geraden ----------------------------------------------------------------------------------------------------------------- v u cos v u v u ___________________________________________________________________________ Neigungswinkel bzw. Schnittwinkel einer Geraden mit einer Ebene ----------------------------------------------------------------------------------------------------------------- 90° mit v n v n v cos oder sin n v n v n ___________________________________________________________________________ Schnittwinkel zweier Ebenen ----------------------------------------------------------------------------------------------------------------- nE n F cos nE nF nE nF Sonderfall: Zueinander senkrechte Ebenen 90° ___________________________________________________________________________