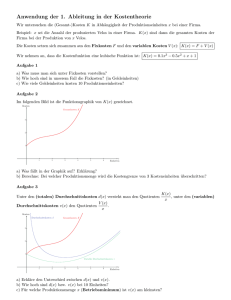
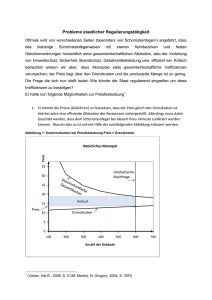
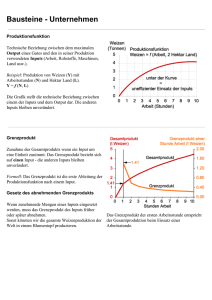
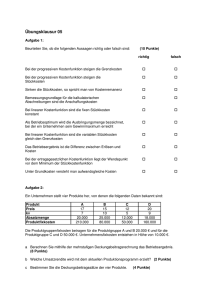
( )( )( xKxExG KEG Kosten Erlöse Gewinn

KAPITEL 2.2
KAPITEL 2.2: ANGEBOTSVERHALTEN VON UNTERNEHMEN
Gliederung
2.2.1 Das Güterangebot von Unternehmen bei vollkommener Konkurrenz
2.2.2 Das Güterangebot eines Monopolisten
Auch im Zusammenhang mit dem Angebotsverhalten einzelner Firmen an
Märkten für Güter und Dienstleistungen gelten die in 2.1 gemachten
grundlegenden Annahmen. Weiter wird angenommen, dass Unternehmen nur
ein Produkt herstellen und dass keine Lagerbildung stattfindet.
Bei
Unternehmen
gibt
es
drei
typische
ökonomische
Entscheidungsprobleme:
• welche Gütermengen sollen angeboten werden? ①
• welche Menge an Produktionsfaktoren (Inputs) sollen für die
Herstellung der Güter eingesetzt werden? ②
• Wieviel soll investiert (entspart) werden? ③
Frage ① zielt auf dieGüterangebotsfunktion ab und wird in diesem
Kapitel behandelt.
Frage ② betrifft v.a. die Arbeitsnachfragefunktion. Hierauf wird in
Kapitel 7 (Arbeitsmarkt) eingegangen.
③ Diese Frage wird nicht Bestandteil dieser Vorlesung sein
2.2.1 Das Güterangebot
Zielvariable einzelner Unternehmen ist der Gewinn, der maximiert werden soll.
Restriktionen sind durch die Güternachfrage und durch andere Unternehmen
gegeben, die dasselbe Gut anbieten. Betrachten wir nun die
Gewinnmaximierung genauer.
Es gilt:
➊
Gewinnfunktion
Gewinn = Erlöse − Kosten
G=E−K
G ( x) = E ( x ) − K ( x )
Der Erlös und die Kosten sind abhängig von der Menge des
hergestellten Gutes. Deshalb ist auch der Gewinn von der
hergestellten Gütermenge x abhängig.
• Notwendige Bedingung für die Gewinnmaximierung: G‘(x) = 0
• Hinreichende Bedingung: G‘‘(x) < 0 Τ Maximum
Gehen wir nun davon aus, dass auf dem Gütermarkt vollkommene
Konkurrenz besteht, d.h., es gibt sehr viele, eher kleinere Unternehmen und
sehr viele, eher kleinere Haushalte. Unter dieser Voraussetzung und unter
Beachtung der weiteren oben erwähnten Annahmen haben einzelne
Unternehmen keinen Einfluss auf die Höhe des Preises ihres Produkts,
sondern müssen den Marktpreis als vorgegeben („als Datum“) hinnehmen.
Dieser Preis sei mit p =p bezeichnet. Hieraus folgt für die notwendige
Bedingung der Gewinnmaximierung:
1
ENTSCHEIDUNGEN EINZELNER UNTERNEHMEN
E ( x) = p ⋅ x
➋
Gewinnmaximierung bei
vollkommener
Konkurrenz
E '( x) = p
G '( x) = E '( x) − K '( x) = 0
E '( x) = K '( x)
p = K '( x)
Begrifflichkeiten:
K‘(x): Grenzkosten: zusätzliche Kosten für die Produktion einer weiteren
Einheit des Gutes X
E‘(x): Grenzerlös: zusätzlicher Erlös bei Verkauf einer weiteren Einheit des
Gutes X.
K' (x)
p
Abb. 2.13.:
Güterangebotsfunktion
bei vollkommener
Konkurrenz.
Güterangebotsfunktion
bei vollkommener
Konkurrenz
xA = f(p)
A
p1
K' (x)
Grenzkostenkurve
(Bereich mit positiver Steigung)
p2
B
Gütermenge X
x2
x1
Abb. 2.13.: Güterangebotsfunktion bei vollkommener Konkurrenz. Die Güterangebotsfunktion eines einzelnen Unternehmens entspricht der Grenzkostenkurve
des Unternehmens. Bei einem Preis vonp1 stellt das Unternehmen eine Gütermenge
von x1 her (Punkt A), weil für x1 gilt:p1 = K‘ (x1). Bei einem Preis vonp2 stellt das
Unternehmen eine Gütermenge von x2 her (Punkt B). Die hergestellte Gütermenge
des Unternehmens ist somit vom Marktpreis und vom Grenzkostenverlauf abhängig.
Definition: Die Güterangebotsfunktion gibt an, wieviel Gütereinheiten x
ein Unternehmen bei alternativen (hypothetischen) Preisen anbieten
würde.
Formal gilt:
xA = f (p) mit f‘ > 0.
Ändern sich – aufgrund äusserer Umstände – die Grenzkosten einer Firma
(Beispiele: Eine zusätzliche Steuer wird erhoben; ein Teil der
Produktionsanlagen ist nach einem Hurrikan unbrauchbar geworden; der
Staat subventioniert die Produktion), verschiebt sich ihre Angebotskurve nach
oben oder unten. Steigt oder fällt die angebotene Menge in der Folge einer
Veränderung des Marktpreises für das betrachtete Gut, spricht man von einer
„Bewegung“ auf der gegebenen Angebotskurve.
2
Definition:
Güterangebotsfunktion
KAPITEL 2.2
Offene Frage: Warum ist der Verlauf der Grenzkostenkurve steigend?
Welcher Kostenverlauf wird unterstellt?
Die Kostenfunktion stellt die Kosten in Abhängigkeit von der
Produktionsmenge eines Gutes dar. Grundsätzlich steigen die Kosten mit
zunehmender Produktionsmenge. Theoretischen Überlegungen und
empirischen Studien zufolge ist ein s-förmiger Verlauf der Kostenkurve
besonders relevant. Er impliziert mit steigender Produktionsmenge zunächst
sinkende Grenzkosten (die Kapazitätsauslastung steigt) bis zu einer Menge,
bei der die Grenzkosten minimal sind, und schliesslich wieder ansteigen
(Kapazitätsüberlastung).
Die Kostenfunktion kann man in zwei Teile aufspalten:
Kostenfunktion
Kosten = Fixkosten + variable Kosten
K (x) = Kfix + Kvar (x)
Definition: Fixkosten sind Kosten, die anfallen, um die Produktionsbereitschaft (Bereitstellen von Material, Miete von Räumlichkeiten und
Maschinen) herzustellen, auch wenn noch nicht ein einziges Stück
produziert wird. Die Fixkosten sind von der produzierten Menge
unabhängig.
Definition:
Fixkosten
Definition: Variable Kosten sind Kosten, die mit der Menge des
produzierten Gutes variieren. Variable Kosten steigen mit zunehmender
Produktionsmenge an.
Definition:
Variable Kosten
3
ENTSCHEIDUNGEN EINZELNER UNTERNEHMEN
Abb. 2.14.:
s-förmiger
Kostenverlauf
Kostenkurve
K (x)
2
K (xMin2)
1
K (xMin1)
Kfix
α2
K' (x)
p
k (x)
α1
xMin1
xMin2
Angebotskurve
2
p2
p1
x
Durchschnittskostenkurve
1
Grenzkostenkurve
xMin1
xMin2
x
Abb. 2.14.: s-förmiger Kostenverlauf. Oben: Die Punkte 1 und 2 liegen auf der sförmigen Kostenfunktion. Vom Abszissenabschnitt bis zum Punkt 1 nimmt die
Steigung der Kostenfunktion mit zunehmender Produktionsmenge ab. Nach diesem
Punkt nimmt die Steigung der Kostenfunktion wieder zu. Der Punkt 1 ist deshalb das
Minimum der Grenzkosten (siehe unten). Im Punkt 2 ist der tan α (Kgesamt (x*)/x*) am
kleinsten, d.h. die gesamten Durchschnittskosten haben hier ihr Minimum. Die
Steigung der Kostenkurve entspricht hier dem Tangentialwinkel α2. Die
Grenzkostenkurve schneidet die gesamten Durchschnittskosten in ihrem Minimum
(siehe unten). Das Minimum der gesamten Durchschnittskosten nennt man das
(langfristige) Betriebsminimum (xmin2). Es liegt dort, wo der Preis die gesamten
Durchschnittskosten deckt. Die Angebotsfunktion eines einzelnen Unternehmens
entspricht dem ansteigenden Ast der Grenzkostenkurve.
Die
Kostenfunktion
eines
Unternehmens
folgt
aus
dessen
Produktionsfunktion. Eine Produktionsfunktion, die einen s-förmigen
Kostenverlauf bedingt, kann durch die allgemeine Form
X = A ⋅ aα ⋅ k β
mit a als eingesetzter Arbeitsmenge und k als eingesetzter Kapitalmenge
angegeben werden. A, α und β sind Parameter, die variieren können.
4
Produktionsfunktion
KAPITEL 2.2
Grundsätzlich kann jede Outputmenge X mit unterschiedlichen Kombinationen
aus a und k hergestellt werden. Die Kostenfunktion gibt dann – bei gegebenen
Preisen für die eingesetzten Produktionsfaktoren – für jede Produktionsmenge
X an, wie hoch die minimal aufzubringenden Produktionskosten (Summe der
Produkte aus eingesetzter Faktormenge und Faktorpreis) sind. Die
Kostenfunktion kann also als Funktion der jeweils effizientesten
(kostengünstigsten) Kombinationen der Produktionsfaktoren angesehen
werden. Nähere Ausführungen finden sich in Kapitel 7 („Arbeitsmarkt“).
Der Zusammenhang zwischen Produktionsfunktion und Kostenfunktion lässt
sich grob anhand der folgenden Abbildung erläutern:
Produktionsfunktion
Kostenfunktion
Kosten
Kosten
Input
Abb. 2.15.:
Produktions- und
Kostenfunktion
Output
Abb. 2.15.: Produktions- und Kostenfunktion. In dieser Abbildung sind
abnehmende Grenzerträge der Produktion unterstellt. Dies schlägt sich in
zunehmenden Grenzkosten nieder.
Mit Hilfe der Produktionsfunktion kann auch der Begriff der Skalenerträge
erläutert werden. Von steigenden (fallenden, konstanten) Skalenerträgen
spricht man dann, wenn ein um einen bestimmten Prozentsatz höherer
Einsatz
der
Produktionsfaktoren
zu
einem
überproportionalen
(unterproportionalen, konstanten) Output-Anstieg führt. Übersetzt auf die
Kostenebene bedeutet dies, dass steigende (fallende, konstante)
Skalenerträge mit fallenden (steigenden, konstanten) Grenzkosten bzw.
langfristigen Durchschnittskosten einhergehen.
Bei vollkommener Konkurrenz und bei s-förmiger Kostenkurve entspricht die
Güterangebotskurve eines Unternehmens dem ansteigenden Ast der Grenzkostenkurve. Auf der Grenzkostenkurve liegt die gewinnmaximale Outputmenge für die jeweilig vorgegebenen Marktpreise (p = K‘ (x)). Nur im
ansteigenden Ast der Grenzkostenkurve ist dabei die hinreichende Bedingung
für ein Gewinnmaximum erfüllt:
!
G‘‘ (x) = E‘‘ (x) – K‘‘ (x) < 0
0 – K‘‘ (x) < 0
K‘‘ > 0 .
Definition:
Betriebsminimum
5
ENTSCHEIDUNGEN EINZELNER UNTERNEHMEN
Definition: Das Betriebsminimum liegt dort, wo die Grenzkosten und die
gesamten Durchschnittskosten gleich gross sind. Bei dieser
Produktionsmenge sind die gesamten Durchschnittskosten minimal.
Liegt der Preis unter dem Betriebsminimum, sind nicht mehr alle Kosten des
Unternehmens gedeckt. Es kann für eine Firma kurzfristig sinnvoll sein,
dennoch ihr Produkt am Markt anzubieten (Deckung der Fixkosten und eines
Teils der variablen Kosten). Langfristig macht ein Angebot bei Preisen
unterhalb des Betriebsminimums ökonomisch keinen Sinn. Kurzfristig stellt
eine Firma ihre Produktion ein, falls der Preis (bei p1) kleiner als die variablen
Durchschnittskosten (VDK) ist:
K' (x)
p
k (x)
Angebotskurve (GK)
p3
TDK
Gewinn
p2
VDK
Betriebsminimum
p1
x3
x
Abb. 2.16.: Variable Durchschnittskosten (VDK) und totale Durchschnittskosten
(TDK).
Langfristig wird eine Firma aus dem Markt austreten, wenn der Preis (bei p2)
kleiner als die totalen Durchschnittskosten (TDK) ist. Die langfristige
Angebotskurve beginnt also bei p2, d.h. im Betriebsminimum, denn nur für
Preise oberhalb von p2 (Beispiel: p3) ist sicher gestellt, dass die Firma einen
Gewinn macht (vgl. Abb. 2.16). Der Gewinn ergibt sich dabei als Fläche
zwischen dem Preis (p3) und den totalen Durchschnittskosten (TDK) and der
Stelle x3 (angebotene Menge).
Bemerkung: Auch für das Güterangebot ist das Elastizitätskonzept relevant.
So gibt etwa die Preiselastizität des Angebots ε x A , p an, um wieviel Prozent die
angebotene Menge steigt oder sinkt, wenn der Preis um ein Prozent steigt
oder sinkt:
εx
A
,p
=
dx A p
⋅
dp x A
Die Preiselastizität des Angebots ist in der Regel positiv, d.h. mit steigendem
Preis steigt auch die angebotene Menge. Die Angebotskurve kann aber auch
vollkommen elastisch oder unelastisch sein.
6
Abb. 2.16.:
Variable und Totale
Durchschnittskosten
KAPITEL 2.2
2.2.2 Das Güterangebot eines Monopolisten
Modifikation: Annahme, dass Unternehmen Monopolist ist.
Definition: Ein Monopol ist eine Marktform, bei der es einen Anbieter
(Monopolist) und sehr viele, eher kleine Nachfrager gibt. Der Monopolist
ist Preissetzer, d.h., der Preis ist nicht vom Markt vorgegeben, sondern
der Monopolist kann den Preis selbst festlegen. Die zugehörige Menge
ergibt sich dann gemäss der Nachfragefunktion.
Definition:
Monopol
Es gibt vor allem drei Gründe für die Entstehung bzw. das Vorhandensein
eines Monopols:
• Ein Unternehmen ist im Besitz von Schlüsselressourcen, über die
kein anderes Unternehmen verfügt (Beispiel: Diamanten).
• Das Monopol wird vom Staat geschaffen, dadurch dass ein
einziges
Unternehmen
mit
der
Bereitstellung
einer
Schlüsseldienstleistung beauftragt wird (Beispiel: Briefpost) oder
dadurch dass Patente bzw. Urheberrechtsschutz gewährt werden
(Beispiele: Medikamente, Bücher, Musik).
• Die Kostenstruktur der Industrie läss es sinnvoll erscheinen, dass
ein Gut nur von einer Firma produziert wird. Dies ist der Fall bei
zunehmenden Skalenerträgen, hohen Fixkosten und tiefen
Grenzkosten. Unter diesen Voraussetzungen kann möglicherweise
eine Firma ein Gut oder eine Dienstleistung mit geringeren
Durchschnittskosten produzieren als zwei oder mehr Firmen.
Auch für ein monopolistisches Unternehmen gilt, dass der Gewinn maximiert
werden soll:
!
G (x) = max
G (x) = E (x) – K (x)
Restriktion: Die gewinnmaximale Menge ergibt sich aus der
Nachfragekurve p = p(x).
G (x) = p (x) x – K (x)
1. Ableitung:
G‘ (x) = p‘ (x)x + 1 p (x) – K‘ (x) = 0
Zeichnen der Grenzerlösfunktion:
Bei linearer Nachfragefunktion, beispielsweise:
p (x) = b – a x
E (x) = p (x) x = (b – a x) x = b x – a x2
E‘ (x) = b – 2 a x
Die Grenzerlösfunktion hat den gleichen Abszissenschnittpunkt wie die lineare
Nachfragefunktion. Die Steigung der Erlösfunktion ist jedoch doppelt so steil
(siehe Abbildung 2.17.).
Die hinreichende Bedinugun für ein Gewinnmaximum ist im Optimalpunkt B
erfüllt (vgl. Abb. 2.17), weil der Schnittpunkt B im ansteigenden Teil der
Grenzkostenkurve liegt. Zu fordern ist:
!
E‘‘ (x) – K‘‘ (x) < 0
7
Gewinnmaximierung
eines Monopolisten
ENTSCHEIDUNGEN EINZELNER UNTERNEHMEN
E‘‘ (x) = -2a
-2a – K‘‘ (x) < 0 ⇒ K‘‘ (x) > -2a .
E' (x)
K' (x)
p
Abb. 2.17.:
Gewinnmaximierung
des Monopolisten
b
Grenzerlösfunktion E' (x)
Grenzkosten K' (x)
A (Cournot-Punkt)
p*
Nachfragefunktion p (x)
Steigung: -2a
x*
Steigung: -a
x
Abb. 2.17.: Gewinnmaximierung des Monopolisten. Im Punkt B sind Grenzkosten
und Grenzerlös gleich gross. Wenn die Menge x* produziert wird, ist der Gewinn des
Monopolisten maximal. Der zugehörige Preis p* liegt auf der Nachfragekurve (Punkt
A). Punkt A wird auch Cournot-Punkt genannt.
Ist die Nachfragekurve gegeben und ebenso die (Grenz-)Kostenkurve, ist das
Güterangebot des Monopolisten durch den Cournot-Punkt charakterisiert.
Ändert sich die Nachfragekurve (z.B. Drehung nach aussen um Punkt b),
ändert sich auch die Lage des Cournot-Punkts.
Literatur
Mankiw, N. G. (1999):★
★ Grundzüge der Volkswirtschaftslehre, Stuttgart,
S. 289–307, Kapitel 12, 13
Taylor, J. B. (2001): Economics, Houghton Mifflin Company, Kapitel 3, 6, 8
Colander, D. (1998): Economics, Irwin/McGraw-Hill, Kapitel 21, 22
★ Empfohlen
8