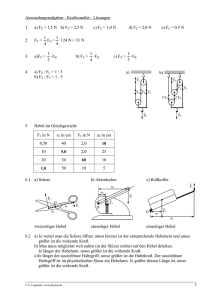
Aufgabendossier Hebelgesetz

10PS/TG - MECHANIK
8
P. Renduli 2009
HEBEL UND DREHMOMENT
53
HEBEL UND DREHMOMENT
8.1
Hebel
Ein Hebel ist ein Kraftwandler, bestehend aus einer steifen Stange, die um einen
Drehpunkt bewegt werden kann. Meistens benutzt man ihn zum Verstärken von Kräften.
Man unterscheidet zwischen dem zweiseitigen und dem einseitigen Hebel.
8.1.1 Zweiseitiger Hebel
Beim zweiseitigen Hebel liegt der Drehpunkt innerhalb der Stange. Beispiele:
Schraubenzieher zum Öffnen
einer Farbdose
Spielwippe
Kneifzange
8.1.2 Einseitiger Hebel
Beim einseitigen Hebel liegt der Drehpunkt an einem Ende der Stange. Beispiele:
Nussknacker
Schubkarre
8.1.3 Weitere Beispiele
Die Photos zeigen weitere Beispiele aus dem Alltag. Entscheide jeweils selbst, um welche
Hebelart es sich handelt!
verschiedene Flaschenöffner
Schraubschlüssel
Bremshebel
10PS/TG - MECHANIK
HEBEL UND DREHMOMENT
P. Renduli 2009
8.2
Hebelgesetz beim zweiseitigen Hebel und 2 wirkenden Kräften
8.2.1
Versuch
54
An einer Seite des Hebels wird durch Anhängen einer Masse eine vertikale Kraft nach
unten ausgeübt. An der anderen Seite wird an unterschiedlichen Stellen mit einem
Kraftmesser nach unten gezogen sodass die Stange wieder horizontal (im Gleichgewicht)
steht. Gemessen werden die Beträge der beiden Kräfte F1 und F2 , sowie die
dazugehörigen Hebelarme a1 und a2 . Darunter versteht man die Entfernung zwischen der
Wirkungslinie der Kraft und dem Drehpunkt des Hebels.
A
a1
B
a2
O
m
F2
F1
8.2.2
Messwertetabelle
F1 (N)
a1 (m)
F2 (N)
a2 (m)
F1·a1 (N·m)
F2·a2 (N·m)
8.2.3 Versuchsauswertung
Zur Auswertung berechnen wir jeweils das Produkt aus Kraft und dem dazugehörigen
Hebelarm. Wir stellen fest, dass das Produkt jeweils gleich ist.
F1 a1
F2 a2
Außerdem stellen wir fest:
Je größer der Hebelarm ist, desto weniger Kraft braucht man, um den Hebel im
Gleichgewicht zu halten.
Je kleiner der Hebelarm ist, desto mehr Kraft braucht man, um den Hebel im
Gleichgewicht zu halten.
10PS/TG - MECHANIK
P. Renduli 2009
HEBEL UND DREHMOMENT
8.3
Hebelgesetz beim einseitigen Hebel und 2 wirkenden Kräften
8.3.1
Versuch
55
Am Hebel wird durch Anhängen einer Masse eine vertikale Kraft nach unten ausgeübt. An
unterschiedlichen Stellen wird mit einem Kraftmesser nach oben gezogen sodass die
Stange wieder horizontal (im Gleichgewicht) steht. Gemessen werden die Beträge der
beiden Kräfte F1 und F2 , sowie die dazugehörigen Hebelarme a1 und a2 .
A
a2
a1
F2
B
O
m
F1
8.3.2
Messwertetabelle
F1 (N)
a1 (m)
F2 (N)
a2 (m)
F1·a1 (N·m)
F2·a2 (N·m)
8.3.3 Versuchsauswertung
Zur Auswertung berechnen wir jeweils das Produkt aus Kraft und dem dazugehörigen
Hebelarm. Wir stellen fest, dass das Produkt jeweils gleich ist.
F1 a1
F2 a2
Wir stellen fest, dass das gefundene Hebelgesetz sowohl für den zweiseitigen als auch
den einseitigen Hebel gilt.
Da das Produkt aus Kraft und Hebelarm ausschlaggebend ist, wie groß die Drehwirkung
einer Kraft ist, definieren wir im nächsten Abschnitt die physikalische Größe Drehmoment
einer Kraft.
10PS/TG - MECHANIK
HEBEL UND DREHMOMENT
P. Renduli 2009
56
8.4
Drehmoment
Eine Kraft kann bei einem drehbar gelagerten Körper eine Drehbewegung um den
Drehpunkt hervorrufen. Die Wirkung der Kraft hängt dabei von ihrem Angriffspunkt ab.
8.4.1 Definition des Drehmoments
Unter einem Drehmoment M versteht man das Produkt aus einer Kraft F und dem
senkrechten Abstand a ihrer Wirkungslinie vom Drehpunkt O.
M
F a
8.4.2 Hebelarm
Den senkrechten Abstand zwischen der Wirkungslinie der Kraft und dem Drehpunkt
bezeichnet man auch als Hebelarm. Die folgenden Beispiele zeigen wie der Hebelarm
bestimmt wird:
O
a
F
O
a
F
a
F
O
8.4.3 Einheit des Drehmoments
Die SI-Einheit des Drehmoments ist das Newtonmeter (Nm):
M
F a
1N 1m 1Nm
Das Newtonmeter darf man in diesem Fall nicht mit dem Joule gleichsetzen. Das
Drehmoment hat in der Tat nichts mit der mechanischen Arbeit zu tun!
8.4.4 Spezialfälle *
Der Versuch zeigt dass:
Eine Kraft, deren Wirkungslinie parallel zur Drehachse ist, bewirkt keine
Drehbewegung.
Eine Kraft, deren Wirkungslinie durch die Drehachse geht, bewirkt keine
Drehbewegung.
In beiden Fällen ist das Drehmoment dieser Kräfte null.
10PS/TG - MECHANIK
P. Renduli 2009
57
HEBEL UND DREHMOMENT
8.5
Hebel bei nicht senkrecht angreifenden Kräften
Bei den bisherigen Beispielen standen die Wirkungslinie der Kraft und die Hebelstange
jeweils senkrecht zueinander. In diesem Fall entspricht der Hebelarm einem Teil der
Hebelstange. Man kann aber auch Kräfte in einem beliebigen Winkel zur Hebelstange
wirken lassen:
In diesem Fall entspricht
der Hebelarm nicht mehr
einem Teil der Hebel–
stange sondern er liegt
außerhalb von ihr und
muss entweder graphisch
oder durch eine Rechnung
bestimmt werden.
a2
A
a1
B
O
m
F2
F1
Der Versuch zeigt, dass je größer (oder kleiner) der Winkel zwischen der Kraft F2 und
der Hebelstange wird, desto größer muss der Betrag dieser Kraft gewählt werden, damit
der Hebel im Gleichgewicht bleibt. In der Tat zeigt die Figur, dass in diesem Fall der
Hebelarm a2 der Kraft kleiner wird. Dadurch wird natürlich auch das entsprechende
Drehmoment kleiner. Damit der Hebel im Gleichgewicht bleibt muss der Betrag der Kraft
erhöht werden.
8.5.1
Beispiel*
Für die folgende Versuchsanordnung soll der Betrag der Kraft F2 zuerst vorausgesagt
werden und dann durch einen Versuch überprüft werden.
C
Das Hebelgesetz ergibt:
F1 a1
a2
A
a1=10cm
Im Punkt B gilt:
130 180
B
O
=130°
m=200g
F2
L=25cm
F1
F2 a2
F2
F1
50
Im rechtwinkligen Dreieck
OBC gilt:
a2
sin
a2 L sin
L
Schließlich können wir schreiben:
F2
F1
F2
F2
a1
L sin
a1
a2
a1
L sin
N
10 cm
0,2 kg 9,81
kg 25 cm sin 50
m g
1,02 N
Der Versuch zeigt, dass der experimentelle und der theoretische Wert übereinstimmen.
10PS/TG - MECHANIK
HEBEL UND DREHMOMENT
P. Renduli 2009
58
8.6
Allgemeines Hebelgesetz
An einem beliebigen Hebel können auch mehrere Kräfte Drehmomente auf die
Hebelstange ausüben. Es soll untersucht werden, wie das allgemeine Hebelgesetz in
diesem Fall formuliert werden kann.
8.6.1
Versuch
Wir versuchen am zweiseitigen Hebel ein Gleichgewicht herzustellen, indem wir bis zu 4
Massen an unterschiedlichen Stellen an die Hebelstange hängen. Wir bestimmen die
Beträge der wirkenden Kräfte, sowie die dazugehörigen Hebelarme und tragen die Werte
in die Tabelle ein.
linksdrehend
rechtsdrehend
O
a1
a2
F1
8.6.2
a4
a3
F2
F3
F4
Messwertetabelle
Linksdrehende Kräfte
Rechtsdrehende Kräfte
F1
a1
F2
a2
F3
a3
F4
a4
(N)
(m)
(N)
(m)
(N)
(m)
(N)
(m)
8.6.3 Versuchsauswertung
Zur Auswertung berechnen wir jeweils die Summe der linksdrehenden Drehmomente Mlinks
und die Summer der rechtsdrehenden Drehmomente Mrechs. Wir stellen fest, dass beide
Werte jeweils gleich sind.
Daraus formulieren wir das allgemeine Hebelgesetz, das für beliebig viele Kräfte gilt.
10PS/TG - MECHANIK
8.6.4
HEBEL UND DREHMOMENT
P. Renduli 2009
59
Allgemeines Hebelgesetz
Wenn der Hebel im Gleichgewicht ist, dann ist die Summe der
linksdrehenden Drehmomente gleich der Summe der
rechtsdrehenden Drehmomente.
8.6.5 Beispiel
Das Beispiel zeigt den zweiseitigen Hebel mit Kräften, die senkrecht zur Hebelstange sind:
rechtsdrehend
O
a1
F1
F2
F3
linksdrehend
a3
a2
a4
F4
Im Fall für den gezeigten Hebel gilt daher durch Anwenden des allgemeinen
Hebelgesetzes:
F1 a1 F2 a2
F3 a3
F4 a4
denn die Kräfte F1 , F2 und F3 bewirken eine Drehung nach links, der die Kraft F4 nach
rechts entgegenwirkt.
10PS/TG - MECHANIK
8.7
P. Renduli 2009
HEBEL UND DREHMOMENT
60
Aufgaben
8.7.1 Schraubenschlüssel
An einem Schraubenschlüssel mit dem wirksamen Hebelarm a1 = 22 cm wirkt eine Kraft
F1 von 60 N. Durch Aufstecken eines Rohres wird der Hebelarm um 200 mm verlängert.
Wie groß ist das Hebeldrehmoment
a. des einfachen Schlüssels?
b. mit dem Aufsteckrohr?
8.7.2 Güterwagen
Ein Güterwagen der Eisenbahn von der Länge L = 12 m und einer Masse von 27 t ist mit
dem vorderen Räderpaar entgleist und soll wieder auf die Schienen gehoben werden. Der
Achsenabstand beträgt d = 8 m, der Schwerpunkt liegt in der Mitte. Welche Kraft ist am
vorderen Ende des Wagens anzusetzen?
8.7.3 Unterschiedliche Hebel
a. Benennen die untenstehenden Hebelarten und ermittele jeweils die erforderliche Kraft
F2, damit Gleichgewicht herrscht.
b. Wie ändert sich die erforderliche Kraft F2 für jeden der gezeichneten Hebel, wenn der
Hebelarm L1 doppelt so lang wird?
8.7.4 Zange
Eine Zange wird nach der Skizze am langen Zangenschenkel mit einer Kraft F1 = 180 N
betätigt. Der Schenkel des Zangenmaules misst bis zum Drehpunkt L2 = 20 mm. Wie lang
muss der Hebelarm L1 gemacht werden, wenn an der Schneide eine Kraft F2 = 1200N
wirken soll?
10PS/TG - MECHANIK
P. Renduli 2009
HEBEL UND DREHMOMENT
61
8.7.5 Mehrere angreifende Kräfte
Ein einseitiger und ein zweiseitiger Hebel sind nach Skizze mit den Kräften F1 bis F4
belastet. Ermittele mithilfe des verallgemeinerten Hebelgesetzes die Kraft F3.
8.7.6 Bockgerüst
Das Bockgerüst (siehe Abbildung) ist mit einem Mörtelkübel von 100 kg Masse und 25
Ziegelsteinen belastet (Masse eines Ziegelsteins: mZ = 3,5 kg).
a. Welche Kraft FA wirkt auf Bock A?
b. Welche Kraft FB wirkt auf Bock B?
Gegeben: L1 = 80 cm, L2 = 120 cm, L3 = 60 cm
Übungen zum Hebel:
Rechne mit g = 10 N/kg.
1.
Wie weit vom Drehpunkt darf der Vater
(m2 = 70 kg) höchstens sitzen, damit ihn das Kind (m1 = 28
kg) mit seiner Gewichtskraft das Gleichgewicht halten
kann?
2.
Welche Kraft wirkt auf die Nuss, wenn du bei A mit 15 N
auf den Nussknacker drückst?
(a = 3,5 cm; b= 7,5 cm)
3.
Mit welcher Kraft drücken die Schneiden der Zange auf
einen Nagel, wenn man bei A mit 100 N drückt? (l1 = 5 cm;
l2 = 1 cm)
4.
Welche Kraft F1 ist erforderlich, um die Schubkarre samt
Inhalt (m = 150 kg) zu heben?
(l1 = 95 cm; l2 = 38 cm)
5.
Wie weit von der Drehachse entfernt muss der Vater
sitzen, damit er die beiden Kinder im Gleichgewicht zu
halten vermag?
(m1 = 45 kg; m2 = 35 kg; m3 = 75 kg)
6.
a) Um wie viele cm dehnt sich bei der nebenstehender
Anordnung die Feder?
Physik Jahrgang 8/9
b) In welchem Abstand x muss die Federkraft angreifen,
wenn sie sich maximal 3,5 cm dehnen darf?
c) wie groß muss D sein, wenn sich die Feder im Abstand
von x = 16 cm um höchstens 1,5 cm dehnen darf?
Lösungen (gerundet):
1.
1,4 m
2.
Angabe ohne Gewähr
47,14 N
3.
500 N
http://home.arcor.de/a-zietlow
4.
428,6 N
5.
3,68 m
http://www.s-hb.de/~zietlow
6.
a) 2,3 cm
b) 12 cm
c) 1750 N/m
=17,5 N/cm
Anwendung des Hebelgesetzes LÖSUNGEN
Beachte, dass die Gewichtskraft mit Hilfe der Masse und des Ortsfaktors berechnet wird: G = m*g
1.
ges. :Länge des Hebelarms in m
linksdrehend : M 1
x 700
Gleichgewicht : M 1
rechtsdrehend : M 2
M2
280 3, 5
x 700 280 3, 5
x 700 980
x 1, 4 m
2.
ges. : Kraft F in N auf die Nuss
linksdrehend : M 1
F 3, 5
Gleichgewicht : M 1
rechtsdrehend : M 2 15 11
M2
F 3, 5 15 11
F 3, 5 165
F 47 N
3.
ges. : Kraft F in N auf den Nagel
linksdrehend : M 1
F 3, 5
Gleichgewicht : M 1
rechtsdrehend : M 2
M2
F 1 100 5
F
4.
500 N
ges. : Kraft F in N zum Heben der Schubkarre
M1
F 133
M 2 1500 38
Gleichgewicht : M 1
M2
F 133 1500 38
133*F = 57000 N
F
5.
429 N
ges. : Kraftarm x in m für den Vater
M1
450 3, 8
M3
x 750
M2
350 3
Gleichgewicht : M 1 M 2
M3
M1 M2
2760 Nm
2760 x 750
x
6a.
15 11
3, 68m
Berechnung der Kraft F, die an der Feder zieht (Hebelgesetz): 10 42 F 18
Berechnung der Ausdehnung s der Feder (Hookesches Gesetz): s
23,3
m
1000
6b. - Berechnung der Kraft für die Ausdehnung von 3,5 cm (Hookesches Gesetz).
- Berechnung der Hebelarmlänge (Hebelgesetz)
F 1000 0, 035N
x 35 10 42
6c.
F
35N
x 12cm
10 42 F 16 und F D 1, 5
10 42 D 1, 5 16
D 17,5
N
N
1750
cm
m
http://home.arcor.de/a-zietlow
http://www.s-hb.de/~zietlow
F
s
23,3N
23,3cm
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A/1/*
a) Gib an, ob es sich bei einer
Wippe um einen einseitigen
oder um einen zweiseitigen
Hebel handelt.
b) Fertige selbst eine Skizze der
Wippe an und zeichne darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte blau
• die Hebelarme der angreifenden Kräfte grün ein.
c) Erläutere schließlich, wie bei einer Wippe das Hebelgesetz angewendet werden kann.
Die Gewichtskraft des Jungen auf der linken Seite beträgt 300N , er sitzt 2 m vom Drehpunkt entfernt.
d) Berechne, in welcher Entfernung von der Drehachse der Junge auf der rechten Seite mit der Gewichtskraft
250N sitzen muss, damit die Wippe im Gleichgewicht ist.
e) Sitzt ein Mädchen auf der rechten Seite 3m von der Drehachse entfernt, so ist die Wippe im Gleichgewicht.
Berechne die Gewichtskraft dieses Mädchens.
f) Erläutere, durch welche Maßnahmen ein kleines Kind auch mit seinem wesentlich schwereren Opa wippen
kann.
© 2004 Thomas Unkelbach; Abbildung aus: Höfling, O.: Physik. Band I. 12.Auflage Bonn 1975. S.54.
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L/1/*
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A / 2 / **
a) Gib an, ob es sich bei einem Flaschenöffner um einen einseitigen oder um einen zweiseitigen Hebel handelt.
b) Fertige selbst eine Skizze des Flascheöffners an und zeichne
darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte blau
• die Hebelarme der angreifenden Kräfte grün ein.
c) Erläutere schließlich, wie beim Flaschenöffner das Hebelgesetz angewendet wird.
Um eine Flasche zu öffnen muss am Rand des Kronkorkens eine
Kraft von 1000N wirken. Der Rand des Kronkorkens liegt
0,5cm vom seinem Mittelpunkt entfernt.
d) Berechne, wie lang der Flaschenöffner mindestens sein muss,
damit man die Flasche mit einer Kraft von 50N öffnen kann.
e) Ein abgebrochener Flaschenöffner ist nur noch 4cm lang.
Berechne, welche Kraft benötigt wird, um die Flasche zu öffnen.
f) Erläutere, durch welche Maßnahmen bei einem Flaschenöffner erreicht werden könnte, dass mit begrenzter
Kraft das Öffnen der Flaschen noch weiter erleichtert wird.
© 2004 Thomas Unkelbach
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L / 2 / **
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A / 3 / **
a) Gib an, ob es sich bei einem Nussknacker um einen
einseitigen oder um einen zweiseitigen Hebel ha ndelt.
b) Fertige selbst eine Skizze des Nussknackers an und
zeichne darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte blau
• die Hebelarme der angreifenden Kräfte grün ein.
c) Erläutere schließlich, wie beim Nussknacker das Hebelgesetz angewendet wird.
In einem Nussknacker ist eine Nuss 3cm von der Drehachse entfernt eingeklemmt. Am Ende der 15cm langen
Griffe des Nussknackers wird eine Kraft von 50N ausgeübt.
d) Berechne die Kraft, die auf die Nuss wirkt.
e) Berechne die Kraft, die man zum Knacken der Nuss benötigt, wenn diese höchstens eine Kraft von 300N
aushält.
f) Erläutere, durch welche Maßnahmen bei einem Nussknacker erreicht werden könnte, dass mit begrenzter
Kraft auch härtere Nüsse geknackt werden können.
© 2004 Thomas Unkelbach; Abbildung aus: Höfling, O.: Physik. Band I. 12.Auflage Bonn 1975. S.59.
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L / 3 / **
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A / 4 / **
a) Gib an, ob es sich bei einer Zange um einen
einseitigen oder um einen zweiseitigen Hebel
handelt.
b) Fertige selbst eine Skizze der Zange an und
zeichne darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte
blau
• die Hebelarme der angreifenden Kräfte
grün ein.
c) Erläutere schließlich, wie bei einer Zange das Hebelgesetz angewendet wird.
Um eine Schraube mit einer Kneifzange durchtrennen zu können, ist an der Schneide die Kraft von 1200N auf
den Draht erforderlich. Der Abstand von der Schneide bis zur Drehachse der Zange beträgt 2cm . Die Hand
kann auf die Za ngengriffe die Kraft von 180N ausüben.
d) Berechne, wie lang die Griffe der Zange mindestens sein müssen, damit der Draht durchtrennt werden kann.
e) Berechne, wie groß die maximale Kraft auf die Schraube an der Schneide wäre, wenn die Griffe der Zange
24cm lang wären.
f) Erläutere, durch welche Maßnahmen bei einer Zange erreicht werden könnte, dass mit begrenzter Kraft
auch härtere Schrauben durchtrennt werden können.
© 2004 Thomas Unkelbach; Abbildung aus: Höfling, O.: Physik. Band I. 12.Auflage Bonn 1975. S.59.
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L / 4 / **
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A/5/*
a) Gib an, ob es sich bei einer Schubkarre um einen einseitigen oder um einen zweiseitigen Hebel handelt.
b) Fertige selbst eine Skizze der Schubkarre an
und zeichne darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte
blau
• die Hebelarme der angreifenden Kräfte grün
ein.
c) Erläutere schließlich, wie bei einer Schubkarre
das Hebelgesetz angewendet wird.
Zwei Säcke Zement mit der Gewichtskraft von ungefähr 1000N liegen auf einer Schubkarre, und zwar ungefähr in der Mitte zwischen der Achse des Rades und den Griffen.
d) Berechne, mit welcher Kraft ein Bauerbeiter die Schubkarre anheben muss.
e) Berechne, wie groß die Gewichtskraft der Ladung höchstens sein dürfte, damit ein Kind mit einer Kraft von
150N die Schubkarre noch anheben könnte.
f) Erläutere, durch welche Maßnahmen bei einer Schubkarre erreicht werden könnte, dass mit begrenzter
Kraft größere Gewichte angehoben werden können.
© 2004 Thomas Unkelbach; Abbildung aus: Höfling, O.: Physik. Band I. 12.Auflage Bonn 1975. S.59.
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L/5/*
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A / 6 / **
a) Gib an, ob es sich bei einer Schere um einen
einseitigen oder um einen zweiseitigen Hebel
handelt.
b) Fertige selbst eine Skizze der Schere an und
zeichne darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte
blau
• die Hebelarme der angreifenden Kräfte grün
ein.
c) Erläutere schließlich, wie bei einer Schere das
Hebelgesetz angewendet wird.
Um ein Blatt normales Papier zu zerschneiden ist eine Kraft von ungefähr 1N nötig. Der Abstand der Griffe
einer Schere zum Drehpunkt ist 10 Mal so groß wie der Abstand des Anfangs der Schneide zum Drehpunkt.
d) Berechne, welche Kraft man benötigt, um ein Blatt Papier zu zerschne iden.
e) Berechne, wie weit die Griffe vom Drehpunkt entfernt sein müssten, damit man mit der gleichen Schere und
der gleichen Kraft auch Pappe schneiden kann, die erst ab einer Kraft von 5N geschnitten wird.
f) Erläutere, durch welche Maßnahmen bei einer Schere erreicht werden könnte, dass mit begrenzter Kraft
auch stärkere Pappe oder sogar Blech geschnitten werden kann.
© 2004 Thomas Unkelbach; Abbildung aus: Höfling, O.: Physik. Band I. 12.Auflage Bonn 1975. S.59.
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L / 6 / **
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A/7/*
a) Gib an, ob es sich bei der abgebildeten Waage um
einen einseitigen oder um einen zweiseitigen Hebel
handelt.
b) Fertige selbst eine Skizze der Waage an und zeichne
darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte blau
• die Hebelarme der angreifenden Kräfte grün ein.
c) Erläutere schließlich, wie bei einer derartigen Waage
das Hebelgesetz angewendet wird.
Der Abstand des rechten Hakens, an den jeweils der Gegenstand mit unbekannter Masse gehängt wird, vom
Drehpunkt beträgt 5cm , das fest an der Waage befindliche Wägestück hat eine Masse von 100g .
d) Berechne, welche Masse der abgebildete Klotz hat, wenn sich im Gleichgewichtszustand das Wägestück
47,5cm vom Drehpunkt entfernt befindet.
e) Berechne, ob mit dieser Waage, bei der der Abstand des Wägestücks zum Drehpunkt maximal 80cm beträgt, eine Masse von ungefähr 1,7 kg noch gewogen werden kann.
f) Erläutere, durch welche Maßnahmen bei dieser Waage erreicht werden könnte, dass noch größere Massen
gewogen werden können.
© 2004 Thomas Unkelbac h; Abbildung aus: Höfling, O.: Physik. Band I. 12.Auflage Bonn 1975. S.59.
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L/7/*
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A / 8 / **
a) Gib an, ob es sich bei der abgebildeten Schranke
um einen einseitigen oder um einen zweiseitigen
Hebel handelt.
b) Fertige selbst eine Skizze der Schranke an und
zeichne darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte blau
• die Hebelarme der angreifenden Kräfte grün ein.
c) Erläutere schließlich, wie bei einer derartigen Schranke das Hebelgesetz angewendet wird.
Der Abstand der Ausgleichsmasse vom Drehpunkt beträgt 75cm , die Länge des linken Teils der Schranke beträgt 3,5m . Man kann das Gewicht des rechten Teils der Schranke vernachlässigen und annehmen, dass das
Gewicht des linken Teils im Schwerpunkt dieses Teils, also im Abstand von 1,75m vom Drehpunkt, angreift.
d) Berechne, wie groß die Ausgleichsmasse sein muss, wenn der linke Teil der Schranke eine Masse von
50kg hat.
e) Berechne, wie weit bei gleicher Masse der Schranke die Ausgleichsmasse vom Drehpunkt entfernt sein
müsste, wenn sie eine Masse von 150kg hätte.
f) Erläutere, durch welche Maßnahmen bei dieser Konstruktion erreicht werden könnte, dass noch längere und
damit schwerere Schranken ausgeglichen werden können.
© 2004 Thomas Unkelbach; Abbildung aus: Höfling, O.: Physik. Band I. 12.Auflage Bonn 1975. S.59.
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L / 8 / **
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A/9/*
a) Gib an, ob es sich bei einem Spaten um einen einseitigen oder um einen
zweiseitigen Hebel ha ndelt.
b) Fertige selbst eine Skizze des Spatens an und zeichne darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte blau
• die Hebelarme der angreifenden Kräfte grün ein.
c) Erläutere schließlich, wie bei einem Spaten das Hebelgesetz angewendet
wird.
Die Länge der Schaufel eines Spatens beträgt 20cm , die Länge des Griffs
1, 20m .
d) Berechne, welche Kraft man aufbringen muss, wenn zum ‚Aufbrechen’ des
Boden eine Kraft von 80N benötigt wird.
e) Berechne, wie ‚hart’ der Boden ist, wenn man zum ‚Aufbrechen’ eine Kraft von 50N benötigt.
f) Erläutere, durch welche Maßnahmen bei einem Spaten erreicht werden könnte, dass mit begrenzter Kraft
das ‚Aufbrechen’ des Bodens noch weiter erleichtert wird.
© 2004 Thomas Unkelbach; Abbildung aus: Höfling, O.: Physik. Band I. 12.Auflage Bonn 1975. S.59.
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L/9/*
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A / 10 / *
a) Gib an, ob es sich bei der abgebildeten Konstruktion um einen einseitigen oder um einen
zweiseitigen Hebel handelt.
b) Fertige selbst eine Skizze dieser Konstruk tion
an und zeichne darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte blau
• die Hebelarme der angreifenden Kräfte
grün ein.
c) Erläutere schließlich, wie bei dieser Konstruktion das Hebelgesetz angewendet wird.
Die abgebildete Stange ist 3,6m lang, die Unterlage befindet sich ungefähr 1, 20m vom linken Ende der Stange
entfernt.
d) Berechne, welche Kraft man am rechten Ende der Stange aufbringen muss, wenn die Kiste eine Masse von
80kg hat.
e) Berechne, wie groß die Masse der Kiste höchstens sein darf, wenn ein Kind mit der Masse 30kg überhaupt
eine Chance hat, die Kiste mit dieser Konstruktion anzuheben.
f) Erläutere, durch welche Maßnahmen bei dieser Konstruktion erreicht werden könnte, dass mit begrenzter
Kraft das Anheben der Kiste noch weiter erleichtert wird.
© 2004 Thomas Unkelbach; Abbildung aus: Höfling, O.: Physik. Band I. 12.Auflage Bonn 1975. S.59.
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L / 10 / *
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
Typ / Nr. / Schwierigkeit
A / 11 / *
a) Gib an, ob es sich bei der abgebildeten Konstruktion um einen einseitigen oder um einen zweiseitigen
Hebel handelt.
b) Fertige selbst eine Skizze dieser Konstruktion an
und zeichne darin
• den Drehpunkt rot
• die Kraftpfeile für die angreifenden Kräfte blau
• die Hebelarme der angreifenden Kräfte grün
ein.
c) Erläutere schließlich, wie bei dieser Konstruktion
das Hebelgesetz angewendet wird.
Die abgebildete Stange ist 3,6m lang, der Schrank 60cm breit und die Stange trifft in der Mitte der Breite des
Schrankes auf den Boden.
d) Berechne, welche Kraft man am rechten Ende der Stange aufbringen muss, wenn der Schrank eine Masse
von 80kg hat.
e) Berechne, wie groß die Masse des Schrankes höchstens sein darf, wenn ein Kind mit der Kraft von 50N
überhaupt eine Chance hat, den Schrank mit dieser Konstruktion anzuheben.
f) Erläutere, durch welche Maßnahmen bei dieser Konstruktion erreicht werden könnte, dass mit begrenzter
Kraft das Anheben des Schrankes noch weiter erleichtert wird.
© 2004 Thomas Unkelbach
Klasse
9
Thema
Physik Sekundarstufe I – Mechanik – Hebel
© 2004 Thomas Unkelbach
Typ / Nr. / Schwierigkeit
L / 11 / *