Lehrplan Sek I - Konrad-Adenauer
Werbung

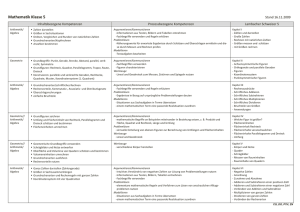
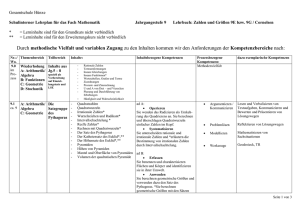
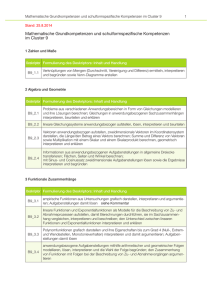
Konrad-Adenauer-Gymnasium Zeitraum 6 Wo. 5 Wo. 8 Wo. 5 Wo. 5 Wo. 6 Wo. Schulinterner Lehrplan Mathematik Lambacher Schweizer 5, Klett-Verlag Inhaltsbezogene Kompetenzen Klasse 5 Prozessbezogene Kompetenzen Natürliche Zahlen (S. 8 – 45) Zählen und darstellen; Große Zahlen Rechnen mit natürlichen Zahlen Größen messen, schätzen und mit ihnen rechnen Erkundungen: Forschung im Reich der Zahlen Darstellen von natürlichen Zahlen und Größen Operieren: Grundrechenarten ausführen Anwenden arithmetischer Kenntnisse Ordnen: Dezimalbrüche ordnen, vergleichen Systematisieren: Anzahlen systematisch bestimmen Symmetrie (S. 46 – 75) Figuren, Achsen- und Punktsymmetrie von Figuren Orthogonale und parallele Geraden Koordinatensysteme Erfassen: Grundbegriffe (Punkt, Gerade, Strecke, Abstand. Radius, parallel, senkrecht, Symmetrie) verwenden und Grundfiguren (Rechteck, Quadrat, Parallelogramm, Dreieck, Kreis) benennen, charakterisieren und in der Umwelt identifizieren Konstruieren einfacher Figuren, auch im Koordinatensystem Operieren: Grundrechenarten ausführen (Kopfrechnen und schriftliche Verfahren) Darstellen von Größen in Sachsituationen mit geeigneten Einheiten Anwenden arithmetischer Kenntnisse; Techniken des Überschlagens und Überprüfens Rechnen (S. 76 – 109) Rechenausdrücke Schriftliche Grundrechenarten: Addition, Subtraktion, Multiplikation und Division von natürlichen Zahlen Bruchteile von Gößen Anwendungen Flächen (S 110 – 139) Größenvergleich von Flächen; Flächeneinheiten Flächeninhalte veranschaulichen Flächeninhalt eines Rechtecks, eines Parallelogramms und eines Dreiecks Umfang einer Fläche Erkundungen: Sportplätze sind auch Flächen Körper (S. 140 – 167) Körper und Netze Quader Schrägbilder Messen von Rauminhalten, Volumenmaßeinheiten Rauminhalt eines Quaders Ganze Zahlen (S. 168 – 201) Negative Zahlen; Anordnung; Zunahme und Abnahme Addieren und Subtrahieren positiver und negativer ganzer Zahlen Multiplizieren und Dividieren ganzer Zahlen Verbindung der Rechenarten Erfassen der Grundfiguren ,Konstruieren grundlegender ebener Figuren (vgl. Symmetrie) Messen: Umfänge von Vielecken, Flächeninhalte von Rechtecken schätzen und bestimmen Darstellen von Größen in geometrischen Sachsituationen mit geeigneten Einheiten Anwenden arithmetischer Kenntnisse in geometrischen Zusammmenhängen Erfassen der geometrischen Grundbegriffe, Grundfiguren (vgl. Symmetrie) und Grundkörper (Quader, Würfel) Konstruieren: Schrägbilder skizzieren, Quadernetze entwerfen, Körper herstellen Darstellen von Größen mit geeigneten Einheiten in Sachsituationen Anwenden arithmetischer Kenntnisse; Techniken des Überschlagens und Überprüfens Darstellen: ganze Zahlen auf verschiedene Weise darstellen (Zahlengerade) Ordnen und Vergleichen von ganzen Zahlen Operieren: Grundrechenarten mit ganzen Zahlen ausführen Anwenden arithmetischer Kenntnisse Konrad-Adenauer-Gymnasium Zeitraum 6 Wo. 6 Wo. 3 Wo. 3 Wo. 8 Wo. 5 Wo. 3 Wo. Schulinterner Lehrplan Mathematik Lambacher Schweizer 6, Klett-Verlag Inhaltsbezogene Kompetenzen Rationale Zahlen (S. 8 – 43) Brüche und Anteile; Kürzen, Erweitern und Ordnen Bruch-Dezimalzahl-Prozentangabe Größen und Einheiten Erkundungen: Teilbarkeit (ggT, kgV) Addition und Subtraktion (S. 44 – 73) Addieren und Subtrahieren von Brüchen und Dezimalzahlen Runden und Überschlagen von Dezimalzahlen Geschicktes Rechnen Winkel und Kreis (S. 74 – 97) Winkel, Winkelarten Winkel schätzen, messen und zeichnen Kreisfiguren Exkursion: Orientierung im Gelände Strategien entwickeln – Probleme lösen (S. 98 – 117) Mathematische Probleme Strategien anwenden Messe, schätzen oder rechnen? Probleme finden Multiplikation und Division rationaler Zahlen (S 118 – 161) Multiplizieren und dividieren von Brüchen Zehnerpotenzen, Maßstäbe Multiplizieren und Dividieren von Dezimalzahlen Grundregeln für Rechenausdrücke – Terme Rechengesetze – Vorteile beim Rechnen Exkursion: Periodische Dezimalzahlen Daten erfassen, darstellen und interpretieren (S. 162 – 191) Relative Häufigkeiten und Diagramme Mittelwerte Boxplots Muster und Abhängigkeiten (S. 193 – 217) Muster erkunden Von Mustern und Termen Muster darstellen Klasse 6 Prozessbezogene Kompetenzen Darstellen: Bruchteile darstellen, als Größen und Verhältnisse deuten. Dezimalzahlen und Prozentzahlen als Darstellungsform für Brüche deuten. Umwandlungen zwischen Bruch, Dezimal- und Prozentzahl. Ordnen: Dezimalbrüche ordnen, vergleichen. Operieren: Rechnungen mit endlichen Dezimalzahlen und einfachen Brüchen ausführen. Erfassen: Grundbegriffe ebener Figuren verwenden: Punkt, Gerade, Strecke, Winkel, Abstand, Radius. Grundfiguren (Rechteck, Quadrat, Parallelogramm, Dreieck,) benennen Konstruieren: Winkel. Kreise, Muster Messen: Winkel schätzen und bestimmen Anwenden: Arithmetische Kenntnisse anwenden; überschlagen, schätzen. Erfassen: Grundfiguren benennen, charakterisieren und in ihrer Umwelt identifizieren. Interpretieren: Muster in Beziehungen zwischen Zahlen erkunden, Vermutungen aufstellen. Operieren: Grundrechenarten mit endlichen Dezimalzahlen und einfachen Brüchen ausführen. Darstellen: Geeignete Brüche in periodische Dezimalzahlen umwandeln; Maßstabsverhältnisse aufstellen und nutzen. Erheben: Daten erheben, in Listen zusammenfassen. Darstellen: Häufigkeitstabellen mit Hilfe von Säulen- und Kreisdiagrammen veranschaulichen Auswerten: Arithmetisches Mittel, Median bestimmen Beurteilen: Statistische Darstellungen interpretieren Darstellen: Beziehungen zwischen Zahlen und Größen in Tabellen und Diagrammen darstellen Interpretieren: Muster in Beziehungen zwischen Zahlen erkunden, Vermutungen aufstellen Systematisieren: Anzahlen auf systematische Weise bestimmen Konrad-Adenauer-Gymnasium Zeitraum Schulinterner Lehrplan Mathematik Lambacher Schweizer 7, Klett-Verlag Inhaltsbezogene Kompetenzen Klasse 7 Prozessbezogene Kompetenzen 5 Wo. Prozente und Zinsen (Seite 8-39) Prozente Prozentsatz, Prozentwert, Grundwert Zinsen, Zinseszins Promille, Rabatt, Skonto, Netto, Tara, Brutto Zusammenhang Brüche – Dezimalbrüche - Prozent Probleme erfassen, erkunden und lösen Kommunizieren, präsentieren und argumentieren Evt. Einsatz des TR zur Lösungskontrolle Zusammenhänge interpretieren 6 Wo. Relative Häufigkeiten und Wahrscheinlichkeiten (S, 40 – 65) relative und absolute Häufigkeit Laplace-Wahrscheinlichkeiten, Summenregel Boxplots erstellen, auswerten und analysieren Probleme erfassen, erkunden und lösen Kommunizieren, präsentieren und argumentieren Evt. Einsatz von TR und PC Einsatz Zusammenhänge interpretieren 6 Wo. Zuordnungen (Seite 66 – 101) Zuordnungen und Graphen, lineare Zuordnungen Proportionale, antiproportionale Zuordnungen Dreisatz Lineare Zuordnungen und Funktionen Probleme erfassen, erkunden und lösen Lösung außer- und innermathematischer Problemstellungen Kommunizieren, präsentieren und argumentieren Einsatz von TR undPC Zusammenhänge interpretieren 6 Wo. Terme und Gleichungen (Seite 102 – 137) Mit Termen Probleme lösen (Waagemodell) Terme umformen, Äquivalenzumformungen, Gleichungen Distributiv-, Kommutativ- und Assoziativgesetz Lösen von Problemen mit geeigneten Strategien Reflektieren, Modellieren, TR, Probleme erfassen, erkunden und lösen Lösung außer- und innermathematischer Problemstellungen Kommunizieren, präsentieren und argumentieren Zusammenhänge interpretieren 6 Wo. Beziehungen in Dreiecken (Seite 138 – 185) Grundkonstruktionen (Lot, Parallelen, Mittelsenkrechte etc.) Dreiecke sortieren Konstruktion von Dreiecken (mit Zirkel und Lineal), Kongruenzsätze Maßstab Transversalen eines Dreiecks (Höhen, Winkelhalbierende, Seitenhalbierende Umkreis, Inkreis, Satz des Thales Winkel, Winkelbeziehungen und –summen Einsatz von mathematischen Werkzeugen (Zirkel, Geodreieck, etc.) Reflektieren, Modellieren, Probleme erfassen, erkunden und lösen Lösung außer- und innermathematischer Problemstellungen Kommunizieren, präsentieren und argumentieren Zusammenhänge interpretieren PC-Einsatz (Geometriesoftware) 6 Wo. Systeme linearer Gleichungen (Seite 186 – 219) Lineare Gleichungssysteme mit 2 Variablen (LGS) Graphisches Lösen Algebraisches Lösen (Einsetzungs-, Gleichsetzung- und Additionsverfahren. Ausblick:: LGS mit 3 Variablen) Äquivalenzumformungen (Gleichungen), Proben Reflektieren, Modellieren, TR, Probleme erfassen, erkunden und lösen Lösung außer- und innermathematischer Problemstellungen Kommunizieren, präsentieren und argumentieren Zusammenhänge interpretieren Konrad-Adenauer-Gymnasium Zeitraum 6 Wo. 4 Wo. 6 Wo. 6 Wo. 8 Wo. 4 Wo. Schulinterner Lehrplan Mathematik Lambacher Schweizer 8, Klett-Verlag Inhaltsbezogene Kompetenzen Reelle Zahlen (S. 8 – 35) Das Radizieren als Umkehrung des Potenzierens anwenden. Wurzeln und Streckenlängen. Rechnen mit Wurzeln. Berechnen von Quadratwurzeln durch Näherung. Rationale und irrationale Zahlen unterscheiden. Formeln umstellen, vereinfachen und auflösen – Binom. Formeln (S. 36 – 52) Terme zusammenfassen, ausmultiplizieren und sie mit einem einfachen Faktor faktorisieren, binomische Formeln als Rechenstrategie nutzen. Flächen und Volumina (S. 53 –75) Flächeninhalt von Dreiecken, Parallelogrammen und Trapezen. Flächeninhalt von Vielecken. Kreise, Kreisteile. Prisma, Zylinder. Zusammengesetzte Figuren. Wahrscheinlichkeitsrechnung (S. 76 – 97) Pfadregel, Wahrscheinlichkeitsverteilung. Ein- und zweistufige Zufallsexperimente mithilfe von Baumdiagrammen veranschaulichen. Pascalsches Dreieck, Binomialverteilung. Funktionen (S. 98 – 139) Lineare und quadratische Funktionen. Aufstellen der zugehörigen Funktionsgleichungen. Geraden und Parabeln in Realsituationen nutzen. Die Parameter der Termdarstellung von linearen und quadratischen Funktionen deuten und dies in Anwendungssituationen nutzen. Definieren, Ordnen und Beweisen (S. 140 – 171) Eigenschaften von Figuren mithilfe der Symmetrie, Winkelsätzen oder der Kongruenz erfassen und begründen. Beweisstrategien und Beweisverfahren – Sätze entdecken. Klasse 8 Prozessbezogene Kompetenzen Ordnen: irrationale und rationale Zahlen unterscheiden und vergleichen. Problemlösen: Untersuchung von Zahlen u. Figuren. Zurückführen auf Bekanntes. Verallgemeinern, Spezialfälle finden. Operieren: Rechnen mit Wurzeltermen. Argumentieren: Präsentation und Bewertung von Lösungswegen. Überprüfen und Bewertung von Problemstellungen. Modellieren: Aufstellen von Gleichungen, Zuordnen zu Realsituationen. Erfassen: Benennen und charakterisieren von Vielecken, Prismen und Zylindern; Identifizierung in ihrer Umwelt. Messen: Schätzen und bestimmen des Flächeninhalts und Umfangs von Kreisen und zusammengesetzten Figuren. Anwenden: Kenntnisse über Körper und Flächen zur Lösung außermathematischer Probleme verwenden. Argumentieren: Informationen aus Texten, Bildern u. Tabellen entnehmen. Mehrschrittige Argumentationen. Modellieren: Aufstellen von Zufallsversuchen zu Realsituationen. Urnenmodelle. Erheben: Datenerhebungen auch mit Tabellenkalkulationen. Interpretieren: Graphen von Zuordnungen und Termen linearer funktionaler Zusammenhänge interpretieren. Modellieren: Aufstellen von Gleichungen, Zuordnungen, Funktionen zu Realsituationen. Anwenden: Lineare und quadratische Funktionen zur Lösung außer- und innermathematischer Problemstellungen anwenden. Erkunden: Muster und Beziehungen bei Figuren untersuchen und Vermutungen aufstellen. Lösen: Anwenden der Problemlösestrategien „Zurückführen auf Bekanntes“, „Spezialfälle finden“ und „Verallgemeinern“. Konrad-Adenauer-Gymnasium Zeitraum 6 Wo. 5 Wo. 6 Wo. 4 Wo. 5 Wo. 6 Wo. 3 Wo. Schulinterner Lehrplan Mathematik Lambacher Schweizer 9, Klett-Verlag Inhaltsbezogene Kompetenzen Quadratische Funktionen quadr. Gleichungen (Seite 8-43) Scheitelpunktbestimmung Quadratischer Gleichungen (quadr, Ergänzung, „p-q“-Formel) Textaufgaben, Anwendungs- und Kompetenzaufgaben Ähnliche Figuren – Strahlensätze (Seite 44 – 69) Ähnlichkeit, ähnliche Dreiecke Zentrische Streckung Zusammenhänge erkennen Textaufgaben, Anwendungs- und Kompetenzaufgaben Maßstab, Planfiguren Formeln in Figuren und Körper (Seite 70 – 105) Satzgruppe des Pythagoras Körperberechnungen (Säulen, Pyramiden, Kegel, Kugel, zusammengesetzte Körper) Textaufgaben, Anwendungs- und Kompetenzaufgaben Maßstab, Planfiguren Potenzen (Seite 106 – 127) Zehnerpotenzen Potenzgesetze Anwendungs- und Kompetenzaufgaben Logarithmus Wachstumsvorgänge (Seite 128 – 149) lineares, exponentielles Wachstum Zinseszins Textaufgaben, Anwendungs- und Kompetenzaufgaben Trigonometrie (Seite 150 – 185) sin, cos, tan am rechtwinkligem Dreieck Anwendungs- und Kompetenzaufgaben Textaufgaben sin, cos, tan am Einheitskreis evt, Sinus- und Kosinussatz Textaufgaben, Anwendungs- und Kompetenzaufgaben Fit für die Oberstufe (Seite 186 – 207) Wiederholung des Unterrichtsstoffes aus SI Prozessbezogene Kompetenzen Probleme erfassen, erkunden und lösen Kommunizieren, präsentieren und argumentieren Einsatz des TR zur Lösungskontrolle Zusammenhänge interpretieren Lösung außer- und innermathematischer Problemstellungen Reflektieren, Modellieren, Probleme erfassen, erkunden und lösen Probleme erfassen, erkunden und lösen Kommunizieren, präsentieren und argumentieren Zusammenhänge interpretieren Einsatz von mathematischen Werkzeugen (Zirkel, Geodreieck, etc.) Reflektieren, Modellieren, Probleme erfassen, erkunden und lösen Lösung außer- und innermathematischer Problemstellungen Einsatz von mathematischen Werkzeugen (Zirkel, Geodreieck, etc.) Reflektieren, Modellieren, Probleme erfassen, erkunden und lösen Lösung außer- und innermathematischer Problemstellungen Kommunizieren, präsentieren und argumentieren Zusammenhänge interpretieren Reflektieren, TR, Probleme erfassen, erkunden und lösen Kommunizieren, präsentieren und argumentieren Zusammenhänge interpretieren Reflektieren, modellieren, Probleme erfassen, erkunden und lösen Lösung außer- und innermathematischer Problemstellungen Kommunizieren, präsentieren und argumentieren Zusammenhänge interpretieren PC und Excel Reflektieren, Modellieren, Probleme erfassen, erkunden und lösen Lösung außer- und innermathematischer Problemstellungen Kommunizieren, präsentieren und argumentieren Zusammenhänge interpretieren PC und Excel Dreieckskonstruktionen als Modell Siehe oben Klasse 9