Formelzeichen und Einheiten

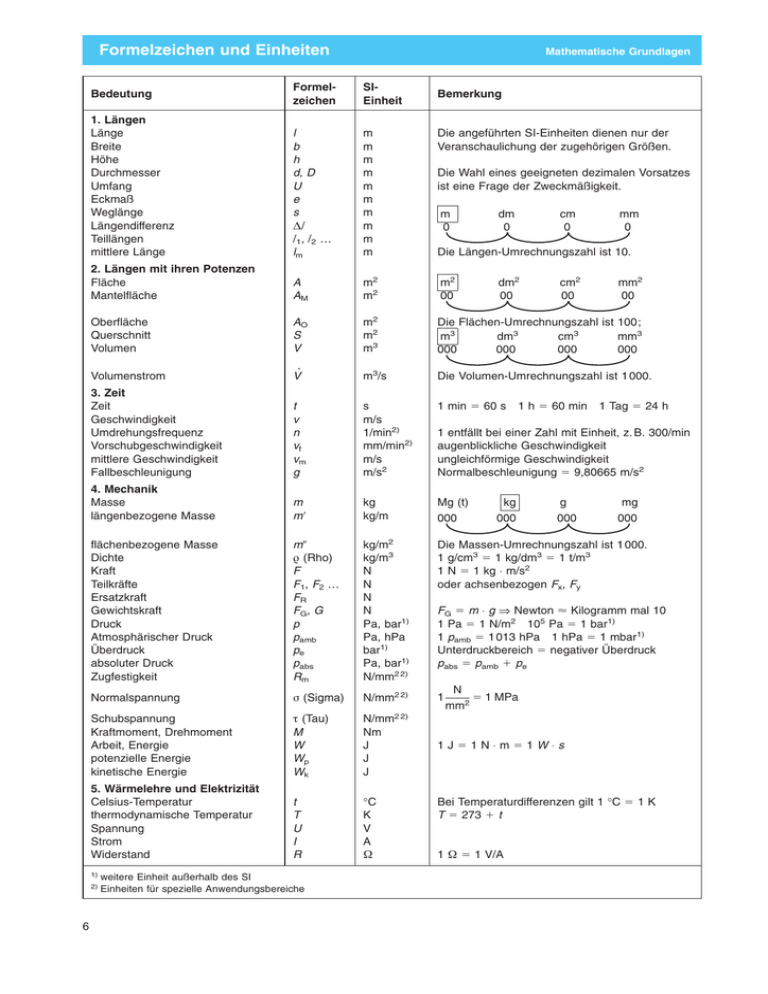
Formelzeichen und Einheiten
Formelzeichen
SIEinheit
1. Längen
Länge
Breite
Höhe
Durchmesser
Umfang
Eckmaß
Weglänge
Längendifferenz
Teillängen
mittlere Länge
l
b
h
d, D
U
e
s
D/
/1, /2 …
lm
m
m
m
m
m
m
m
m
m
m
Die angeführten SI-Einheiten dienen nur der
Veranschaulichung der zugehörigen Größen.
2. Längen mit ihren Potenzen
Fläche
Mantelfläche
A
AM
m2
m2
m2
00
Oberfläche
Querschnitt
Volumen
AO
S
V
m2
m2
m3
Die Flächen-Umrechnungszahl ist 100;
m3
dm3
cm3
mm3
000
000
000
000
Volumenstrom
.
V
m3/s
Die Volumen-Umrechnungszahl ist 1 000.
3. Zeit
Zeit
Geschwindigkeit
Umdrehungsfrequenz
Vorschubgeschwindigkeit
mittlere Geschwindigkeit
Fallbeschleunigung
t
v
n
vf
vm
g
s
m/s
1/min2)
mm/min2)
m/s
m/s2
1 min 5 60 s
4. Mechanik
Masse
längenbezogene Masse
m
m9
kg
kg/m
Mg (t)
000
flächenbezogene Masse
Dichte
Kraft
Teilkräfte
Ersatzkraft
Gewichtskraft
Druck
Atmosphärischer Druck
Überdruck
absoluter Druck
Zugfestigkeit
m0
r (Rho)
F
F1, F2 …
FR
FG, G
p
pamb
pe
pabs
Rm
kg/m2
kg/m3
N
N
N
N
Pa, bar1)
Pa, hPa
bar1)
Pa, bar1)
N/mm2 2)
Die Massen-Umrechnungszahl ist 1 000.
1 g/cm3 5 1 kg/dm3 5 1 t/m3
1 N 5 1 kg ⋅ m/s2
oder achsenbezogen Fx, Fy
Normalspannung
s (Sigma)
N/mm2 2)
1
Schubspannung
Kraftmoment, Drehmoment
Arbeit, Energie
potenzielle Energie
kinetische Energie
t (Tau)
M
W
Wp
Wk
N/mm2 2)
Nm
J
J
J
1J51N⋅m51W⋅s
5. Wärmelehre und Elektrizität
Celsius-Temperatur
thermodynamische Temperatur
Spannung
Strom
Widerstand
t
T
U
I
R
°C
K
V
A
Z
Bedeutung
1)
2)
6
Mathematische Grundlagen
weitere Einheit außerhalb des SI
Einheiten für spezielle Anwendungsbereiche
Bemerkung
Die Wahl eines geeigneten dezimalen Vorsatzes
ist eine Frage der Zweckmäßigkeit.
m
0
dm
0
cm
0
mm
0
Die Längen-Umrechnungszahl ist 10.
dm2
00
cm2
00
mm2
00
1 h 5 60 min 1 Tag 5 24 h
1 entfällt bei einer Zahl mit Einheit, z. B. 300/min
augenblickliche Geschwindigkeit
ungleichförmige Geschwindigkeit
Normalbeschleunigung 5 9,80665 m/s2
kg
000
g
000
mg
000
FG 5 m ⋅ g ⇒ Newton ø Kilogramm mal 10
1 Pa 5 1 N/m2 105 Pa 5 1 bar1)
1 pamb 5 1 013 hPa 1 hPa 5 1 mbar1)
Unterdruckbereich 5 negativer Überdruck
pabs 5 pamb 1 pe
N
5 1 MPa
mm2
Bei Temperaturdifferenzen gilt 1 °C 5 1 K
T 5 273 1 t
1 Z 5 1 V/A
Lösen von Aufgaben
1. Allgemeine Hinweise
Mathematische Grundlagen
Jeder Wert einer physikalischen Größe kann als Produkt aus Zahlenwert und
Einheit dargestellt werden:
Größenwert
5 Zahlenwert 3 Einheit
Länge l
Fläche A
5 310
5 248
mm
cm2
Hinweis
Zwischen Zahlenwert und Einheit wird kein Multiplikationszeichen gesetzt.
Zahlenwert und Einheit sind als selbstständige Faktoren zu behandeln.
Wenn sich die Einheit ändert, so ändert sich auch der Zahlenwert.
2. Aufgabenstellung
Für ein dreieckiges Knotenblech wird eine Fläche von 248 cm2 benötigt.
Berechnen Sie für 310 mm Seitenlänge die erforderliche Breite in cm.
Lesen Sie den Aufgabentext langsam mit Überlegung und stellen Sie sich
den Sachverhalt deutlich vor! Halten Sie dabei möglichst die Zusammenhänge
skizzenhaft fest!
Schreiben Sie die gesuchten und gegebenen Größen sauber mit Formelzeichen und Einheit heraus:
3. Grundgleichung
Gesucht
b in cm
Gegeben
A 5 248 cm2
l 5 310 mm
Bringen Sie die erkannten Zusammenhänge auf die jeweilige Grundgleichung, hier:
A 5
l⋅b
2
Erst dann ist nach der gesuchten Größe aufzulösen:
2⋅A
b 5
l
Gesucht
b in cm
Gegeben
A 5 248 cm2
l 5 310 mm 5 31 cm
Vorüberlegung
Grundgleichung in Worten
Lösung
A 5
l⋅b
2
2⋅A
b 5
l
2 ⋅ 248 cm2
5
31 cm
b 5 16 cm
Nebenrechnung
496 ; 31 5 16
31
2
186
186
2
0
b
4. Lösungsgang
Hinweis
Achten Sie auf die schrittweise Ausführung der Rechnung. Es empfiehlt sich,
vor der Ausrechnung eine Überschlagsrechnung vorzunehmen.
Führen Sie ferner durch das Mitnehmen und Kürzen der eingesetzten Einheiten den Nachweis der Einheitenkontrolle durch.
5. Zusammenfassung
Die Problemdurchdringung erfolgt in drei Stufen:
Lesen Sie bewusst – erfassen Sie mit Einsicht – überprüfen Sie mit Verständnis.
Bringen Sie die Zusammenfassung der Problemlage auf die Grundgleichung.
7
Rechnen mit Brüchen
Mathematische Grundlagen
Zähler zählt die Teile (Dividend)
Nenner nennt die Teilungszahl (Divisor)
Bruch Teil vom Ganzen (Quotient)
1. Bruchbegriff
Brüche entstehen bei der Teilung eines Ganzen, z. B.
Zähler
Dividend
1 2 3 4 5
, , , , 5
5
5 Quotient
4 4 4 4 4 Nenner
Divisor
Folgerung Jeder Bruch stellt eine Division dar. Jede gemischte Zahl lässt
1 5
sich als Bruch darstellen, z. B. 1 5
4 4
2. Addition
Gleichnamige Brüche (Brüche mit gleichem Nenner) werden addiert, indem
man ihre Zähler addiert und den Nenner beibehält
3 1 311 4
1 5
5 51
4 4
4
4
Ungleichnamige Brüche (Brüche mit ungleichem Nenner) werden addiert,
indem man sie zuerst auf einen gemeinsamen Nenner bringt
3
3 2 3 ⋅ 5 1 2 ⋅ 4 23
1 5
5
51
4 5
4⋅5
20
20
3. Subtraktion
Gleichnamige Brüche werden subtrahiert, indem man ihre Zähler subtrahiert
und den Nenner beibehält
3 1 321 2 1
2 5
5 5
4 4
4
4 2
Ungleichnamige Brüche werden subtrahiert, indem man sie zuerst auf einen
gemeinsamen Nenner bringt
3 2 3⋅522⋅4
7
2 5
5
4 5
4⋅5
20
4. Multiplikation
Brüche werden multipliziert, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert
6
3
3 2 3⋅2
⋅ 5
5
5
4 5 4 ⋅ 5 20 10
5. Division
Brüche werden dividiert, indem man den ersten Bruch mit dem Kehrwert des
zweiten Bruches multipliziert
3 2 3 5 15
7
; 5 ⋅ 5
51
4 5 4 2
8
8
6. Zusammenfassung
Nur gleichnamige Brüche lassen sich addieren und subtrahieren. Eine
ganze Zahl kann als Scheinbruch mit dem Nenner 1 dargestellt werden.
Multiplikation
5 Bruch I ⋅ Bruch II
Division
5 Bruch I ⋅ Kehrwert von Bruch II
7. Beispiele
8
54
2
6/8 gekürzt ergibt 3/4
3/4 mit 2 erweitert 6/8
a b c ayz 1 bxz 1 cxy
1 1 5
x y z
xyz
2 3
Kehrwert von ist
3 2
2
x
225
x58
3
3
8;25
14
Divisionszeichen oder Bruchstrich sind gleichwertige Rechenzeichen.
Kürzen, d. h. Zähler und Nenner durch die gleiche Zahl dividieren.
Erweitern, d. h. Zähler und Nenner mit der gleichen Zahl multiplizieren.
Der Hauptnenner ist das kleinste gemeinsame Vielfache aller Einzelnenner.
Der Hauptnenner wird unter einen gemeinsamen Bruchstrich gesetzt.
Den Kehrwert erhält man, indem Zähler und Nenner vertauscht werden.
Bruchgleichungen werden nach den Regeln der Gleichungslehre aufgelöst.
Aufgaben
Rechnen mit Brüchen
Kürzen von Brüchen
24 ⋅ 36 ⋅ 15 ⋅ 16 ⋅ 3
1. a)
12 ⋅ 27 ⋅ 8
3x ⋅ (a 1 b) ⋅ (a 2 b)
2. a)
15 ⋅ (a 2 b) ⋅ (a 1 b)
Erweitern von Brüchen
12ax
mit 3bz
3. a)
21cy
2x 2 3y 1 5z
mit ab
4. a)
24
36a 2 24b 1 12c 2 6
6
6ab 2 12a 1 10b 2 3
b)
6ab 2 12a 2 20b 2 6
b)
5b 1 4c 2 3y
mit d
3x
3
b) 5
8 12x 2 15y 2 3z
b)
abx 2 acx 1 adx 2 ax
ax
ax 1 ay 1 bx 1 by
c)
ax 2 bx 1 ay 2 by
c)
a1b2c1d2e
mit 2x
a2b
3x 2 12y
5
c)
4
4x 2 4y
c)
Addition und Subtraktion von gleichnamigen Brüchen
3 5 6 2
5xy 7xy 10xy
1
2
5. a) 1 2 1
b)
7 7 7 7
2x
2x
32x
9a
12b
ax 1 z bx 1 z
6a
2
2
2
6. a)
b)
a2b
a2b
a2b a2b a2b
2a 1 4b 2a 2 2b
1
3x
3x
3a 2 5b 2a 2 7b
2
c)
2x 2 3y 2x 2 3y
c)
Addition und Subtraktion von ungleichnamigen Brüchen
3
2
2
2 3 2 1
5
2
6
7. a) 1 2 1
b) x 1 x 1 z
c) ab 2 1 a 2 2 a
3 4 5 2
4
5
3
3
3
5
2x 12y 5x 3y
3x 2y 2x 3
9x 2 6y 7x 2 3y
2
1
1
1
1
2 11
2
8. a)
b)
c)
2x 2 2y 3x 2 3y
3
24
8
12
4
3
3
4
1
2 1
1
Multiplikation von Brüchen
2 4 3 2
12ax 24cy 3
⋅
⋅ d
9. a) ⋅ ⋅ ⋅ ⋅ 3,5
b)
3 5 4 7
8dy 36a 4
3x 5x 6x 2
a 2cd
⋅ (2b)
2
1
⋅
10. a) a 1 ⋅
b)
b ab
4y 6y 9y 3
1
2
Division von Brüchen
2 4 1 1
11. a) ; ; ; ; 2
3 5 2 3
ab 1 bx
; (a 1 x)
12. a)
a
1
2
15a 12a 4ab
;
;
35x 3x 6xy
bx 1 abx x 1 ax
;
b)
b
a
b)
Multiplikation und Division von Brüchen
3ab 6ab 36mx
1 2 3⋅2⋅4
;
⋅
13. a) ; ⋅
b)
2 3 4⋅6⋅8
4x
3x 24nx
4 (x 1 y) 4x 1 4y
(a 1 b) (c 2 d) x
;
⋅
;
14. a)
b)
x
y
y
2x
y
2
7
3
2
1
xy ⋅
⋅ 2 ⋅ 12 ⋅
8
4x 3
3
1
1
2
1
c) 2 x 2 1 y 1 2 z 1
3
2
3
2
c)
1
2
c)
113 abc2 ; 125 bc2
c)
6abc
4a 2 2b
;
3x 1 9 23x 2 9
c)
11 3 x 1 4 x2 ⋅ 3 x ; 4 xy
c)
a1b x r1s
1
⋅ ;
⋅
2x 3
6x a 1 b
4
2
1
3
2
5
Wissen – Erkennen – Werten
Erklären Sie: Bruch und Scheinbruch, Zähler und Nenner.
Welcher Zusammenhang besteht zwischen Bruchstrich und Divisionszeichen?
Beschreiben Sie mithilfe eines Beispiels das Erweitern und Kürzen.
Unter welchen Voraussetzungen können Brüche addiert oder subtrahiert werden?
Zeigen sie auf, wie man Dezimalbrüche in gewöhnliche Brüche umwandelt.
Nennen sie technische Anwendungsbeispiele für die Bruchrechnung.
ap
ap
c
a)
b)
c)
d)
e)
f)
2
15
Interpretieren von Darstellungen
a, b
x
ZE
Fachstützende Grundlagen
vorhandene Größen
gesuchte Größe
Zeicheneinheit
Hinweis
Größe 5 Zahlenwert 3 Einheit
1. Beziehungen
Jede Aufgabe lässt sich auf eine Abhängigkeit von zwei oder mehreren
Größen zurückführen. Die abhängige, veränderliche Größe nennt man Funktion.
Größen:Dem Kreisumfang ist der Durchmesser zugeordnet U 5 f(d) ⇒ y 5 f(x)
v 5 f(t) ⇒ y 5 f(x)
Der Geschwindigkeit ist die Zeit zugeordnet
Hinweis
Zuordnungen können mit Zahlenleitern, Leitertafeln oder in Diagrammen
(Netztafeln, Schaubildern) verdeutlicht werden.
2. Zahlenleiter
Zahlenleiter werden eingesetzt, wenn zwei veränderliche Größen von einer
Konstanten abhängen, z. B. Temperaturvergleich °C mit K.
Aufbau: Zwei zueinander in einem bestimmten Verhältnis stehende Größen
werden auf einer Zahlenleiter gegenübergestellt.
Hinweis
Durch eine Zahlenleiter kann eine funktionelle Beziehung übersichtlich auf
kleinstem Raum dargestellt werden.
3. Leitertafel
Mit Leitertafeln wird die gesuchte Größe in Abhängigkeit von mehreren
bekannten Größen grafisch ermittelt.
Aufbau: Die drei Leitern haben gleichen, parallelen Abstand voneinander.
Die mittlere Leiter hat bei x 5 a 6 b halbe Zeicheneinheit.
Hinweis
Für eine Gleichung mit drei Größen sind drei parallele Geraden erforderlich,
die im gewünschten Ablesebereich mit Zahlen zu versehen sind.
4. Diagramm
Grafische Darstellungen im Koordinatensystem nennt man allgemein Diagramme, die durch die Punktverbindung entstandene Linie Graph oder Schaulinie.
Graph: Gleicher Zuwachs der Zuordnungen ergibt als Schaulinie
eine Gerade.
Ungleicher Zuwachs der Zuordnungen ergibt als Schaulinie
eine Kurve.
Hinweis
Bei metrischer Achsenteilung ist die Schaulinie eine Gerade oder Kurve.
Bei logarithmischer Achsenteilung ist die Schaulinie stets eine Gerade.
5. Zusammenfassung
6. Beispiel
Zahlenleitern, Leitertafeln und Diagramme sind nomografische1) Rechenhilfen, mit denen die gesuchte Größe grafisch ermittelt wird.
Die mechanische Arbeit W eines Körpers ist von dem Weg s und der Kraft F
abhängig. Überprüfen Sie den Zusammenhang mit nebenstehender Leitertafel.
Lösung
Schnittpunkt F-W-s
Wertetabelle
Vorüberlegung
F in N
1
2
3
s in cm
W in Ncm
1
1
2
4
3
9
4
5
Arbeit 5 Kraft 3 Weg
4 5
16 25
Anmerkung
Bei einer Gleichung y 5 a ⋅ b hat die mittlere Leiter mit logarithmischer Teilung
die halbe Zeicheneinheit.
1)
34
nomos (griechisch) 5 Gesetz, Regel
Aufgaben
Wärmedehnung
Berechnen Sie die fehlenden Werte für einen Profilstahl:
1. Aufgabe
Anfangslänge in mm
Temperaturdifferenz in K
Längenänderung in mm
a
b
c
1 000
1
?
1 000
?
1,2
?
200
2,4
2. Aufgabe
a
l 1 in m
Dt in °C
Dl in mm
b
1
2
100 ?
?
4,8
c
?
100
1,8
3. Das Ausdehnungsmaximum einer 20 m langen Eisenbahnschiene ist bei 14 °C
9,36 mm. Welche Ausgangstemperatur wurde zugrunde gelegt?
4. Ein 14 m langer Brückensteg wurde bei 18 °C montiert. Im Sommer erwärmte sich
die Brücke auf 48 °C. Um welches Maß verlängert sie sich?
5. Eine 755 mm lange Stahlwelle musste beim Drehen zwischen Stirnseitenmitnehmer und Körnerspitze um 1 mm gelockert werden. Die Werkstatttemperatur betrug
20 °C. Wie hoch war die Erwärmung?
6. Eine Stahlbrücke hat bei 20 °C eine Länge von 80 m. Man rechnet im Sommer mit
einer Erwärmung bis auf 65 °C. Wie viel mm Spalt müssen aufgrund der Temperaturschwankung frei bleiben?
7. Eine 3 m lange Profilleiste verlängerte sich bei Erwärmung von 15 °C auf 85 °C
um 5,05 mm. Aus welchem Werkstoff besteht das Profil?
8. Eine Cu-Freileitung hat bei 20 °C eine Länge von 52 m. Im Sommer steigt die
Temperatur auf 48 °C. Wie groß ist die Längenzunahme?
9. Eine 14 m lange Aluminiumschiene hat sich – bei 18 °C gemessen – im Betrieb
auf 14,04 m verlängert. Wie groß war die Erwärmung?
10. Ein Wälzlager von 60 mm Durchmesser wird zum Aufziehen in Öl von 20 °C auf
80 °C erwärmt. Um wie viel mm vergrößert sich der Innendurchmesser?
11. Ein Stahlring mit 79,95 mm Innenbohrung soll auf eine 80 mm dicke Welle aufgeschrumpft werden. Messtemperatur ist 20 °C. Auf welche Temperatur muss der
Ring mindestens erwärmt werden?
c
a)
b)
c)
d)
e)
f)
g)
Wissen – Erkennen – Werten
Begründen Sie, warum bei Temperaturdifferenzen für 1 °C 5 1 K gesetzt wird.
Beweisen Sie die Ausdehnungsgleichung: l 2 5 l 1 ⋅ (1 1 al ⋅ Dt).
Zeigen Sie den Zusammenhang zwischen Längen- und Volumenausdehnung auf.
Was geschieht, wenn ein erwärmter Körper sich nicht frei ausdehnen kann?
Nennen Sie Fälle, bei denen die Wärmeausdehnung berücksichtigt werden muss.
Wann können Bauteile aus verschiedenen Werkstoffen gepaart werden?
Unterscheiden Sie die Begriffe „Dehnen“ und „Schrumpfen“.
Stahl
S235
5
S27
Stahl
55
Gestreckte Längen
L
gestreckte Länge in mm
d m mittlerer Durchmesser in mm
s
Materialdicke in mm
Fertigungs- und Prüftechnik
D Außendurchmesser in mm
d Innendurchmesser in mm
n Anzahl der Biegekanten
l1, l2 Teillängen in mm
Hinweis
Gestreckte Länge 5 Ausgangslänge für Biegeteile.
Biegelänge
Beim Biegen werden die äußeren Werkstofffasern durch Zugspannungen
gestreckt, die inneren Fasern durch Druckspannungen verkürzt.
Folgerung
Man errechnet gestreckte Längen auf einer neutralen Faser, die frei von
mechanischen Spannungen ist.
1. Vollring
Länge vor dem Biegen 5 mittl. Durchmesser ⋅
L
5
dm
⋅
Hinweis
mittl. Durchmesser
mittl. Durchmesser
2. Zusammengesetzte Länge
p
p
5 Außendurchmesser 2 Materialdicke
5 Innendurchmesser 1 Materialdicke
Die gestreckte Länge setzt sich aus den Teillängen zusammen.
a
L 5 dm ⋅ p ⋅
1 l2 1 …
360°
Hinweis
Richtwerte für die Wahl von Biegeradien sowie Schwerpunktslagen von Werkstoffprofilen sind den Tabellenbüchern zu entnehmen.
3. Ecke gestaucht
Gestreckte Länge 5 Länge der Mittellinie
L
5 Summe der Außenmaße 2 n ⋅ s
L
5 Summe der Innenmaße 1 n ⋅ s
Hinweis
Bei symmetrischem Querschnitt geht die neutrale Faser durch den Mittelpunkt.
4. Zusammenfassung
5. Beispiel
Für regelmäßige Querschnitte (z. B. Kreis, Quadrat, Rechteck) gilt:
Gestreckte Länge 5 Länge ihrer neutralen Faser
Aus einem Vierkantstahl mit der Abmessung 30 3 30 mm ist ein Ring mit
200 mm Innendurchmesser herzustellen. Welche Stablänge in mm ist erforderlich?
Gesucht
L in mm
Gegeben
s 5 30 mm
d 5 200 mm
Lösung
L 5 dm ⋅ p
L 5 230 mm ⋅ p
Vorüberlegung
Gestr. Länge 5 Länge der Mittellinie
L 5 722,6 mm
Hinweis
Achten Sie stets auf die Durchmesserangabe
(Innen- oder Außendurchmesser).
64
Aufgaben
Regelmäßige Vierecke
1. Verwandeln Sie in:
a) m2: 3,8 dm2, 0,78 cm2,
b) cm2: 6,3 m2, 0,66 dm2,
c) dm2: 9,8 cm2, 0,31 m2,
d) mm2: 4,3 dm2, 0,04 m2,
3 140 mm2,
2 130 mm2,
6 186 mm2,
7 281 cm2,
0,04 cm2,
0,03 dm2,
0,23 m2,
2,12 cm2,
31,4 dm2,
86,4 m2,
22,2 cm2,
0,21 dm2,
3,8 mm2
2,4 mm2
0,2 mm2
0,003 m2
Die fehlenden Werte sind zu berechnen:
2. Rechteck
Länge in cm
Breite in cm
Fläche in cm2
a
b
c
40
25
?
50
?
180
?
4,5
270
3. Rhomboid
l in m
b in dm
A in cm2
a
b
c
0,2
1,5
?
0,3
?
750
?
3,5
1 400
4. Es wird eine Abdeckplatte mit den Maßen 760 3 760 mm benötigt. Berechnen Sie
den notwendigen Blechbedarf in m2.
5. Für eine Träger-Versteifung wird ein Blech in Rhombusform benötigt. Die Grundseite wird mit 182 mm und die Senkrechte dazu mit 153 mm gemessen. Ermitteln
Sie den Flächenbedarf in cm2.
6. Eine Blechtafel ist 1 200 mm lang und 580 mm breit. Berechnen Sie den Flächeninhalt in m2.
7. Für ein Nummernschild werden 5,72 dm2 Blech verarbeitet. Ermitteln Sie bei
bekannter Grundseite von 52 cm die Breite in mm.
8. Für eine Blechtür werden 1,89 m2 Blech benötigt. Die Tür ist 0,9 m breit. Berechnen Sie die Türhöhe in mm.
9. Die Grundseiten einer rechteckigen Ölwanne verhalten sich wie 2 : 5 bei einem
Flächeninhalt von 0,162 m2. Der Flächeninhalt soll um 3,4 dm2 vergrößert werden.
Bestimmen Sie die neuen Seiten in cm.
10. Ein Quadrat von 120 mm Seitenlänge soll in ein flächengleiches Rechteck von
85 mm Breite verwandelt werden. Wie lang wird die Grundseite?
11. Ein Rhomboid von 140 mm Länge und 60 mm Breite soll in ein flächengleiches
a) Rechteck von 110 mm Länge, b) Quadrat, c) in einen flächengleichen Rhombus
von 80 mm Breite verwandelt werden.
c
a)
b)
c)
Wissen – Erkennen – Werten
Erläutern Sie, wie viel Ausdehnungen eine Fläche besitzt.
Worauf ist beim Umrechnen von Flächeneinheiten zu achten?
Vergleichen Sie die Bezeichnungen Parallelogramm, geradlinig begrenzte Flächen
und regelmäßige Vierecke.
Rhomboid (Parallelogramm)
69
Ohm’sches Gesetz
U
R
I
Elektrotechnik
Spannung, gemessen in V (Volt)
Widerstand, gemessen in Z (Ohm)
Stromstärke, gemessen in A (Ampere)
1. Grundgrößen
Zur Verdeutlichung der elektr. Grundgrößen betrachten wir einen unter Druck
stehenden Wasserhahn:
Wasserdruck Z
Wassermenge Z
Drosselung
Z
2. Beziehungen
Elektronendruck
Z
Elektronenfluss
Z
Elektronenbehinderung Z
Spannung
Stromstärke
Widerstand
Gleich bleibender Widerstand bewirkt bei Spannungserhöhung gleichzeitige
Stromerhöhung.
Versuchsreihe: R 5 100 Z (konstant)
Spannung in V
100
200
300
1
2
3
Stromstärke in A
Gleich bleibende Spannung bewirkt bei Widerstandserhöhung gleichzeitige Stromverringerung.
Versuchsreihe: U 5 200 V (konstant)
3. Ohm’sches Gesetz
Widerstand in Z
25
50
100
Stromstärke in A
8
4
2
Aus diesen beiden Beziehungen I , U und I , 1/R erhalten wir das
Ohm’sche Gesetz:
I
5
U
R
(Zweckmäßig U 5 R ⋅ I geschrieben)
Merke
Das Ohm’sche Gesetz beschreibt die Wechselbeziehung zwischen U, R und I.
4. Zusammenfassung
Das Ohm’sche Gesetz gilt für Gleichstrom, für Wechselstrom nur bei
ohmscher Belastung.
U5R⋅I
5. Beispiel
Eine Glühlampe nimmt bei einer Spannung von 3,6 Volt einen Strom von 0,2
Ampere auf. Welchen Widerstand besitzt der Glühdraht?
Gesucht
R
Gegeben
U 5 3,6 V
I 5 0,2 A
Lösung
U 5 R⋅I
U
R 5
I
3,6 V
R 5
0,2 A
R 5 18 Z
Vorüberlegung
U5R⋅I
Beachte
Setzen Sie die Grundgrößen stets als V, A, Z an.
112
Lernfeldübergreifende
Arbeitsaufträge
Fertigungs- und Prüftechnik: Druckprüfventil
Schwerpunkte
– Technische Kommunikation (Skizzieren, Bemaßung)
– Werkstofftechnik (Halbzeuge, Kurzname)
– Prüftechnik (Gewindegrößen, Maßtoleranzen)
– Berechnungen (Masse, Druck, Hebelgesetz)
– Fertigungstechnik (Spanen, Fügen, Richtwerte)
– Technische Unterlagen (CNC-, vc-d-Diagramm)
Allgemeintoleranzen ISO 2768-m
2
1
1
1
1
1
1
Spannstift
Rändelschraube
Gegengewicht
Hebelstange
Ventilkörper
Lagerbock
Ventilgehäuse
4 u 15
M5 u 10
DIN EN ISO 8752
DIN 653
55 Si 7
5.8
S235JRG1
S235JRG1
S235JRG1
S235JRG1
S235JRG1
7
6
5
4
3
2
1
Rundstahl
Flachstahl
Rundstahl
Flachstahl
Sechskantstahl
DIN EN 10278 – 20 u 18
DIN EN 10278 – 20 u 8 u 125
DIN EN 10278 – 25 u 50
DIN EN 10278 – 15 u 30
DIN EN 10278 – 55 u 60
Lernbereichsübergreifende Arbeitsaufträge
P1 Kommunikation
1. Lesen Sie die Gesamtzeichnung, erläutern Sie die Funktion der Einzelteile.
2. Zeigen Sie auf, bei welchen Teilen Kraft-, Form- oder Stoffschluss auftreten.
3. Welche Beanspruchungsarten werden bei Belastung des Ventils wirksam?
4. Warum eignet sich das Gewinde M 42 3 2 besonders als Befestigungsgewinde?
5. Welchen Einfluss hat die Steigung des Gewindes auf die Anpresskraft?
6. Nennen Sie besondere Anforderungen an die Funktionssicherheit des Ventils.
P2 Werkstofftechnik
1. Erläutern Sie die in der Stücklistenspalte aufgeführten Halbzeuge.
2. Ermitteln Sie für die erforderlichen Halbzeuge die längenbezogene Masse.
3. Was bedeutet in der Stückliste der Spalte Werkstoff die Angabe S235JRG1?
4. Erläutern Sie den Unterschied zwischen Zugfestigkeit und Streckgrenze.
5. Erklären Sie für den Spannstift (Pos. 7) die Werkstoffangabe 55 Si 7.
6. Entschlüsseln Sie die Bezeichnung: Rändelschraube DIN 653-M5 3 10 – 5.8
P3 Prüftechnik
1. Nennen Sie die Kenngrößen, die zur Überprüfung des Gewindes dienen.
2. Welche Gewindegrößen können mit dem Messschieber ermittelt werden?
3. Zeigen Sie Möglichkeiten auf, das fertige Gewinde M 42 3 2 zu prüfen.
4. Ermitteln Sie für das Befestigungsgewinde M 42 3 2 den Flankendurchmesser.
5. Nennen Sie mögliche Prüffehler bei der Fertigungs- und Funktionskontrolle.
6. Erstellen Sie für die Fertigung eine Liste mit den erforderlichen Prüfgeräten.
P4 Fertigungstechnik
1. Zeigen Sie auf, welche Fragen bei der Fertigung im Mittelpunkt stehen.
2. Nach welchen Gesichtspunkten ist die Werkstoffauswahl zu treffen?
3. Begründen Sie die anwendungsbezogenen Fertigungsverfahren.
4. Erläutern Sie grundlegende Vorgänge und Einflüsse beim Spanen.
5. Nennen Sie wichtige Unfallverhütungsvorschriften für die Fertigung der Teile.
6. Welche Maschinen und Werkzeuge sind für die Fertigung bereitzustellen?
126