Uebungen_3_2
Werbung
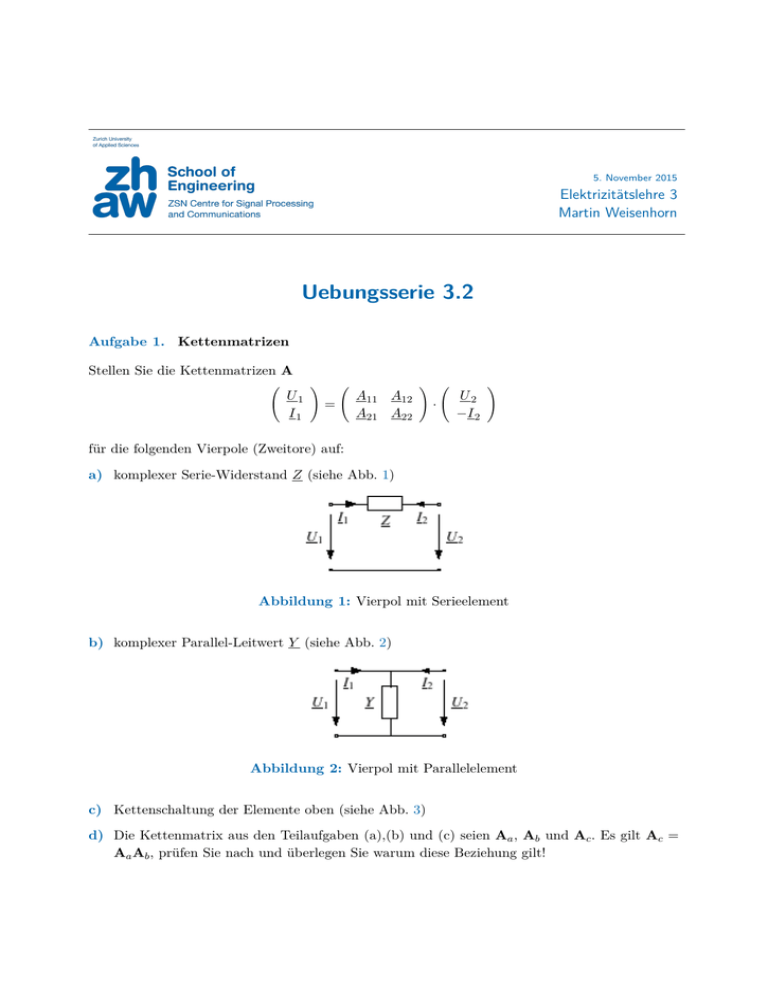
5. November 2015 Elektrizitätslehre 3 Martin Weisenhorn Uebungsserie 3.2 Aufgabe 1. Kettenmatrizen Stellen Sie die Kettenmatrizen A U1 I1 ! = A11 A12 A21 A22 ! · U2 −I 2 ! für die folgenden Vierpole (Zweitore) auf: a) komplexer Serie-Widerstand Z (siehe Abb. 1) Abbildung 1: Vierpol mit Serieelement b) komplexer Parallel-Leitwert Y (siehe Abb. 2) Abbildung 2: Vierpol mit Parallelelement c) Kettenschaltung der Elemente oben (siehe Abb. 3) d) Die Kettenmatrix aus den Teilaufgaben (a),(b) und (c) seien Aa , Ab und Ac . Es gilt Ac = Aa Ab , prüfen Sie nach und überlegen Sie warum diese Beziehung gilt! Uebungsserie 3.2, Elektrizitätslehre 3 2 Abbildung 3: Vierpol mit Serie und Parallelelement Aufgabe 2. Idealer Übertrager Ein idealer Übertrager mit dem SpannungsübersetzungsverU hältnis ü12 = U 1 ist sekundärseitig mit dem komplexen Widerstand Z 2 belastet. Primärseitig 2 wird ein Funktionsgenerator mit der Leerlaufspannung U 0 = U0 und dem Innenwiderstand R0 angeschlossen. a) Lesen Sie die Kettenmatrix des idealen Übertragers aus dem Skript. b) Bestimmen Sie die primärseitige Spannung U 1 durch Transformation des Widerstands Z 2 auf die Primärseite. c) Bestimmen Sie die sekundärseitige Spannung U 2 durch Transformation der linearen Quelle auf die Sekundärseite. Aufgabe 3. Frequenzgang des verlustlosen Übertragers I1 I2 k12 U1 L1 L2 U2 R2 Abbildung 4: Verlustloser Übertrager √ Gegeben sei ein verlustloser Übertrager mit den Kenngrössen L1 , L2 , L12 = k12 L1 L2 , bzw. 0 < k12 < 1 welcher sekundärseitig mit einem Widerstand R2 belastet ist. Z U a) Bestimmen Sie die mit R2 normierte Frequezgangfunktion R12 = R2 I1 und skizzieren Sie 1 deren Amplitudengang. Bringen Sie diesen Frequenzgang in die folgende normierte Form und identifizieren Sie die Parameter k, ωg1 und ωg2 : Z jω 1 + =k R2 ωg1 1 + jω ωg2 jω ωg1 Hinweis: Benutzen Sie die Kettenmatrix A des verlustlosen Übertragers und die durch den Lastwiderstand gegebene Beziehung U2 = R2 (−I2 ). Uebungsserie 3.2, Elektrizitätslehre 3 3 b) Welchen Wert muss der Kopplungsfaktor k12 mindestens aufweisen, damit die Schaltung sich primärseitig über mindestens eine Dekade von Frequenzen wie ein Widerstand verhält? Aufgabe 4. (Verlustloser) Transformator Bei Transformatoren werden typischerweise folgende Parameter angegeben: primäre Nennspannung: U1n sekundäre Nennspannung: U2n Nennleistung (sekundär): S2n Nennbetriebsfrequenz: f Windungszahlverhältnis: ü12 relative Kurzschlussspannung (bei I1n ): uk N1 N2 (Angabe üblicherweise in %) = Bemerkung: Die Wahl von ü12 als Windungszahlverhältnis führt auf das lineare, verlustlose, „symmetrische T-Ersatzmodell“ des Transformators. Aus den gegebenen Parametern lassen sich folgende Grössen direkt bestimmen: sekundäre Nennstromstärke: I2n sekundäre Nennslast: Z2n absolute Kurzschlussspannung: U1k S2n U2n 2 U2n = S2n = uk · U1n = a) Bestimmen Sie die absolute Kurzschlussspannung U1k wenn bei sekundärseitigem Kurzschluss primärseitig die Nennstromstärke I1n fliesst. Letztere entspricht der primärseitungen Stromstärke, wenn sekundärseitig die Nennlast unter Nennspannung steht. Hinweis: Gehen Sie von dem Stromübertsetzungsverhältnis II12 und den folgenden Beziehungen bei U2 = 0 aus: ! ! ! U1 jωL1 jωL12 I1 = · U2 jωL12 jωL2 I2 mit p L12 = k12 L1 L2 b) Wie verhält sich die relative Kurzschlussspannung in Funkiton des Kopplungsfaktors k12 ? Aufgabe 5. Linearisiertes Transformatormodell Gegeben sei ein 6 MVA Wechselstromtransformator 5 kV:100 kV / 50 Hz mit folgenden Daten: Wirksamer Kernquerschnitt: Scheitelwert der magnetischen Flussdichte: AF e = 0.187 m2 B̂ = 1.5 T (Annahme: sinusförmiger Verlauf) Uebungsserie 3.2, Elektrizitätslehre 3 4 Im Leerlauf wird bei U1n = 5 kV die (primärseitige) Leerlaufleistung P10 = 8.8 kW gemessen. Dabei fliesst die Stromstärke I10 = 2.6 A. Im Kurzschluss wird bei der (primärseitigen) Kurzschlussspannung U1k = 571 V die Kurzschlussleistung P1k = 30 kW gemessen. Dabei fliessen primär- und sekundärseitig die Nennströme: I1n ≈ üI2n . 12 Vereinfachend wird ausserdem angenommen, dass ü12 = N1 N2 ≈ U1n U2n . a) Bestimen Sie das Übersetzungsverhältnis ü12 und die Nennstromstärken I1n und I2n . b) Berechnen Sie die Windungszahlen N1 und N2 . dφ dB Hinweis: u2 (t) = dψ dt = N2 dt = N2 AF e dt , Es gilt Φ̂ = AF e B̂ c) Bestimmen Sie den Eisenverlustwiderstand RF e und die Hauptinduktivität Lh aus den Leerlaufmessdaten. Welche Werte habe dabei die Stromstärken IF e und Ih in diesen Elementen? d) bestimmen Sie die primär- und sekundärseitigen Werte der Kupferverlustwiderstände RCu1 , RCu2 und Streuinduktivitäten Lσ1 , Lσ2 aus den Kurzschlussmessdaten. Bemerkung: Das so ermittelte Modell liefert nur approximative Werte und dies aus mehreren Gründen: Das Modell ist linear, was im Allgemeinen bei Transformatoren nicht zutrifft und das Spannungsübersetzungsverhältnis ist, ausgenommen bei Transformatoren mit einem Kopplungsfaktor sehr nahe bei 1, nicht identisch mit dem Windungszahlverhältnis. Lösung 1. Kettenmatrizen a) komplexer Serie-Widerstand Z U1 I1 ! U1 I1 ! ! = 1 Z 0 1 ! = 1 Y ! · U2 −I 2 ! · U2 −I 2 b) komplexer Parallel-Leitwert Y 0 1 c) Kettenschaltung der Elemente oben U1 I1 ! = 1 + Z 1Y 2 Z 1 Y2 1 ! · U2 −I 2 ! d) Siehe Lösung der vorangegangenen Aufgabe. Kettenmatritzen sind so konzipiert, dass sich Serienschaltungen durch Multiplikation der entsprechenden Kettenmatritzen rechnen lassen. Uebungsserie 3.2, Elektrizitätslehre 3 5 Lösung 2. Idealer Übertrager U Ein idealer Übertrager mit dem Spannungsübersetzungsverhältnis ü12 = U 1 ist sekundärseitig 2 mit dem komplexen Widerstand Z 2 belastet. Primärseitig wird ein Funktionsgenerator mit der Leerlaufspannung U 0 = U0 und dem Innenwiderstand R0 angeschlossen. a) Lesen Sie die Kettenmatrix des idealen Übertragers aus dem Skript. U1 I1 ! = ü12 0 0 1 ü12 ! · U2 −I 2 ! b) Bestimmen Sie die primärseitige Spannung U 1 durch Transformation des Widerstands Z 2 auf die Primärseite. Z 02 = ü212 Z 2 ü212 Z 2 U U1 = R0 + ü212 Z 2 0 c) Bestimmen Sie die sekundärseitige Spannung U 2 durch Transformation der linearen Quelle auf die Sekundärseite. R000 = U 000 = U2 = 1 R0 ü212 1 U ü12 0 U0 Z2 1 R0 + Z 2 ü12 ü2 12 Lösung 3. Frequenzgang des verlustlosen Übertragers Gegeben sei ein verlustloser Übertrager (L1 , L2 , L12 , bzw. 0 < k12 < 1) welcher sekundärseitig mit einem Widerstand R2 belastet ist. Z U a) Bestimmen Sie die mit R2 normierte Frequenzgangfunktion R12 = R2 I1 und skizzieren Sie 1 deren Amplitudengang. Bringen Sie diesen Frequenzgang in die folgende normierte Form Uebungsserie 3.2, Elektrizitätslehre 3 6 und identifizieren Sie die Parameter k, ωg1 und ωg2 : 1 1 U1 Z1 = R2 R2 I1 U2 1 1 a11 U2 + a12 (−I2 ) 1 a11 + a12 R2 1 a11 U2 + a12 R2 = = R2 a21 U2 + a22 (−I2 ) R2 a21 U2 + a22 U2 R2 a21 + a22 R1 2 R2 q 2 √ 1−k12 L1 1 1 L 2 1 k12 L2 + jω k12 L1 L2 R2 1 1 + jω(1 − k12 ) R22 q = = L2 1 1 R2 R2 √ + 1 L2 1 jωL1 + L1 R2 = k12 jωk12 L1 L2 = = = L1 R2 2 L jωL1 1 + jω(1 − k12 ) R22 L2 R2 1 + jω R 2 L2 L1 1 + jωσ R2 jω L2 R2 1 + jω R 2 ω 1 + j jω ωg2 k ωg1 1 + j ωωg1 2 : Der Koeffizientenvergleich liefert mit σ = 1 − k12 ωg1 = ωg2 = k = R2 L2 1 R2 ωg1 = > ωg1 σ L2 σ L1 L2 b) Welchen Wert muss der Kopplungsfaktor k12 mindestens aufweisen, damit die Schaltung sich primärseitig über mindestens eine Dekade von Frequenzen wie ein Widerstand verhält? 1 ≥ 10 σ → k12 = √ 1 − σ ≥ 0.95 Lösung 4. (Verlustloser) Transformator Bei Transformatoren werden typischerweise folgende Parameter angegeben: primäre Nennspannung: U1n sekundäre Nennspannung: U2n Nennleistung (sekundär): S2n Nennbetriebsfrequenz: f Windungszahlverhältnis: ü12 relative Kurzschlussspannung (bei I1n ): uk N1 N2 (Angabe üblicherweise in %) = Uebungsserie 3.2, Elektrizitätslehre 3 7 Bemerkung: Die Wahl von ü12 als Windungszahlverhältnis führt auf das lineare, verlustlose, „symmetrische T-Ersatzmodell“ des Transformators. Aus den gegebenen Parametern lassen sich folgende Grössen direkt bestimmen: sekundäre Nennstromstärke: I2n sekundäre Nennslast: Z2n absolute Kurzschlussspannung: U1k S2n U2n U2 = 2n S2n = uk · U1n = a) Bestimmen Sie die absolute Kurzschlussspannung U1k wenn bei sekundärseitigem Kurzschluss primärseitig die Nennstromstärke I1n fliesst. Letztere entspricht der primärseitungen Stromstärke, wenn sekundärseitig die Nennlast unter Nennspannung steht. Hinweis: Gehen Sie von dem Stromübertsetzungsverhältnis II12 und den folgenden Beziehungen bei U2 = 0 aus: ! ! ! U1 jωL1 jωL12 I1 = · jωL12 jωL2 U2 I2 Bei Kurzschluss gilt U 2k = 0. Mit Bedingung I 1k = I 1n erhält man I 2k L12 = − I = −k12 L2 1k U 1k L2 = jω L1 − 12 L2 s L1 I L2 1n ! 2 I 1n I 1k = jωL1 1 − k12 b) Wie verhält sich die relative Kurzschlussspannung in Funktion des Kopplungsfaktors k12 ? Bei kleinen Kopplungsfaktoren ist die Kurzschlussspannung nahezu identisch mit der Nennspannung U1n . Solche Transformatoren sind kurzschlussfest. Im Gegensatz dazu wird bei „guter“ Kopplung die Kurzschlussspannung wesentlich kleiner als die Nennspannung. Wird so ein Transformator bei Nennspannung sekundärseitig kurzgeschlossen, so wird eine viel grössere Stromstärke primärseitig fliessen als die Nennstromstärke! Lösung 5. Linearisiertes Transformatormodell Gegeben sei ein 6 MVA Wechselstromtransformator 5 kV:100 kV / 50 Hz mit folgenden Daten: Wirksamer Kernquerschnitt: Scheitelwert der magnetischen Flussdichte: AF e = 0.187 m2 B̂ = 1.5 T (Annahme: sinusförmiger Verlauf) Im Leerlauf wird bei U1n = 5 kV die (primärseitige) Leerlaufleistung P10 = 8.8 kW gemessen. Dabei fliesst die Stromstärke I10 = 2.6 A. Uebungsserie 3.2, Elektrizitätslehre 3 8 Im Kurzschluss wird bei der (primärseitigen) Kurzschlussspannung U1k = 571 V die Kurzschlussleistung P1k = 30 kW gemessen. Dabei fliessen primär- und sekundärseitig die Nennströme: I1n ≈ üI2n . 12 Vereinfachend wird ausserdem angenommen, dass ü12 = N1 N2 ≈ U1n U2n . a) Bestimen Sie das Übersetzungsverhältnis ü12 und die Nennstromstärken I1n und I2n . ü12 ≈ S1n U1n S2n = U2n I1n = ≈ I2n ≈ U1n 5 kV = = 0.05 U2n 10 kV 6 MW = 1.2 kA 5 kV 6 MW = 60 A 100 kV dφ dB b) Berechnen Sie die Windungszahlen N1 und N2 . Hinweis: u2 (t) = dψ dt = N2 dt = N2 AF e dt √ √ 2U2n Û2 = 2U2n = N2 AF e ω B̂ ≈ 1600 → N2 = 2πf B̂AF e √ √ 2U1n Û1 = 2U1n = N1 AF e ω B̂ → N1 = ≈ 80 2πf B̂AF e c) Bestimmen Sie den Eisenverlustwiderstand RF e und die Hauptinduktivität Lh aus den Leerlaufmessdaten. Welche Werte habe dabei die Stromstärken IF e und Ih in diesen Elementen? P10 = U1n I10 cos ϕ10 → cos ϕ10 = IF e = I10 cos ϕ10 = 1.76 A → RF e ≈ Ih = I10 sin ϕ10 = 1.91 A → P10 = 0.677 U1n I10 (induktiv) U1n = 2.8 kΩ IF e 1 U1n Lh ≈ = 8.3 H ω Ih d) bestimmen Sie die primär- und sekundärseitigen Werte der Kupferverlustwiderstände RCu1 , RCu2 und Streuinduktivitäten Lσ1 , Lσ2 aus den Kurzschlussmessdaten. P1k = U1k I1n cos ϕ1k U1k cos ϕ1k ≈ 20.8 mΩ I1n 1 U1k sin ϕ1k Lσ = ≈ 1.51 mH ω I1n RCu = → → → P1k = 0.0438 (induktiv) U1k I1n RCu 1 RCu1 = ≈ 10 mΩ RCu2 = 2 RCu1 ≈ 4.2 Ω 2 ü12 Lσ 1 Lσ1 = ≈ 0.76 mH RCu2 = 2 Lσ2 ≈ 0.30 H 2 ü12 cos ϕ1k = Bemerkung: Das so ermittelte Modell liefert nur approximative Werte und dies aus mehreren Gründen: Das Modell ist linear, was im Allgemeinen bei Transformatoren nicht zutrifft und das Spannungsübersetzungsverhältnis ist, ausgenommen bei Transformatoren mit einem Kopplungsfaktor sehr nahe bei 1, nicht identisch mit dem Windungszahlverhältnis.