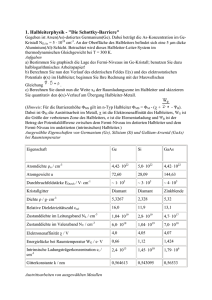
Anhang zum Abschnitt Festkörper 1 −= i
Werbung

Anhang zum Abschnitt Festkörper 1. 2. 3. 4. 5. Hintergrund Im Abschnitt verwendete Symbole Akronyme Gleichungen Zitate 1. Hintergrund Drude schlägt 1900 ein einfaches Modell zur Beschreibung des Ladungstransports in Metallen vor [1]. Dieses Modell wurde mehrfach erweitert ohne das ursprüngliche Konzept eines Elektronengases zu verwerfen. Es führte schließlich zu einem auf der Quantenmechanik basierendem Bändermodell des Festkörpers. Dieses Modell erlaubt es in vielen Fällen den Ladungstransport im Halbleiter auch weiterhin klassisch als „Gas“ geladener Teilchen zu betrachten und ermöglicht zudem eine oftmals befriedigende Beschreibung der Wechselwirkung ungebundener Ladungsträger mit den Gitteratomen [2,3,4]. 2. Im Abschnitt verwendete Symbole Symbol α c Physikalische Größe Absorptionskoeffizient Vakuumlichgeschwindi gkeit Diffusionskonstante für Elektronen Diffusionskonstante für Löcher Energie Fermi-Energie Leitungsbandkante Valenzbandkante Besetzungswahrscheinli chkeit Besetzungswahrscheinli chkeit der Elektronen im Leitungsband Besetzungswahrscheinli chkeit der Löcher im Valenzband Kraft Zustandsdichte Zustandsdichte der Elektronen im Leitungsband Zustandsdichte der Löcher im Valenzband Plancksche Konstante i Imaginäre Einheit imaginary unit I j Intensity Current density Wm-2 Am-2 jdiff jdrift jn jp kB Intensität Konvektionsstromdicht e Diffusionsstromdichte Driftstromdichte Elektronenstromdichte Löcherstromdichte Boltzmannkonstante Diffusion current density Drift current density Electron current density Hole current density Boltzmann Constant ke Wellenvektor des Wave number of the Am-2 Am-2 Am-2 Am-2 1,381×10-23J/K = 8,617×10-5eV/K cm-1 Dn Dp E EF ELB EVB f fe fh F g gc gv h Englische Übersetzung Absorption coefficient Speed of light in vacuum Einheit/Wert cm-1 2,998x108ms-1 Diffusivity of electrons (diffusion coefficient) Diffusivity of holes m2s-1 Energy Fermilevel Conduction band edge Valence band edge Probability of occupancy J, Ws, eV J, Ws, eV J, Ws, eV J, Ws, eV force Density of states Electron density of states in the conduction band N cm-3 cm-3 Hole density of states in the valence band Planck constant cm-3 m2s-1 6,626×10-34Js = 4,136×10-15eVs h/2π i = −1 Bemerkung λ me0 m e* mh* µ µe µh n NA NANc ND ND+ Nv ∇n ∇p p pe Q q Elektrons Wellenlänge Ruhmasse des Elektrons Effektive Masse des Elektrons Effektive Masse des Lochs Beweglichkeit Elektronenbeweglichkei t Löcherbeweglichkeit Elektronendichte Akzeptorkonzentration Dichte der ionisierten Akzeptoren Äquivalente Zustandsdichte im Leitungsband Donatorkonzentration Dichte der ionisierten Donatoren Äquivalente Zustandsdichte im Valenzband Konzentrationsgradient der Elektronen Konzentrationsgradient der Löcher Löcherdichte Impuls des Elektrons Elektrische Ladung Wg Betrag der Elementarladung Elektrischer Widerstand Elektrische Ladung Elektrische Leitfähigkeit Elektrische Leitfähigkeit der Elektronen Zeit Temperatur Freie Flugzeit Betrag der Elektronengeschwindig keit Thermische Geschwindigkeit Gruppengeschwindigke it Mittelwert des Geschwindigkeitsvektor Bandabstand Wkin ω Kinetische Energie Kreisfrequenz R ρ∗ σ σn t T τc ve vth vg ¢v² electron Wavelength rest mass of the electron m, nm, µm 9.109×10-31 kg Effective mass of electron Effective mass of hole g, kg Mobility Electron mobility cm2/(Vs) cm2/(Vs) Hole mobility cm2/(Vs) cm-3 cm-3 cm-3 Acceptor density Ionized acceptor density g, kg i.a. ein Tensor, da (Kristall)richtungsabhängig i.a. ein Tensor, da (Kristall)richtungsabhängig Effective density of states cm-3 in the conduction band Donor density Ionized donor density cm-3 cm-3 Effective density of states cm-3 in the valence band concentration gradient of electrons concentration gradient of holes Hole density pulse Electric Charge Absolute value of the Elementary Charge Resistance Electrical Charge Electrical conductivity Electron conductivity cm-4 cm-4 cm-3 kgms-1 C, As 1,602×10-19C Ω C, As Sm-1, (Ωm)-1, (Ωcm)-1 Sm-1, (Ωm)-1, (Ωcm)-1 Mit Berücksichtigung der Polarität Skalar im isotropen Medium ansonsten ein Tensor Skalar im isotropen Medium ansonsten ein Tensor Time Temperature s K s Value of electron velocity ms-1 Thermal velocity ms-1 group velocity ms-1 Velocity, speed ms-1 band gap eV Angular frequency eV, J 2πν Hz (rad/s) Gemittelt über alle Richtungen des Raums Energiedifferenz zwischen Valenzbandkante und Leitungsbandkante Die Angabe rad/s vermeidet die Verwechslung mit der Frequenz ν. Wellenfunktion Komplex konjugierte Wellenfunktion ψ ψ* 3. 4. Wave function − − Akronyme Akronym Bezeichnung Übersetzung c-Ge Crystalline Germanium Kristallines Germanium c-Si Crystalline Silicon Kristallines Silizium DOS Density of States Zustandsdichte FCC Face Centered Cubic Kubisch flächenzentriert i-Si intrinsic Silicon Intrinsisches (undotiertes) Silizium n-Si n doped Silicon n dotiertes Silizium p-Si p doped Silicon p dotiertes Silizium Si:B Boron doped Silicon Bor dotiertes Silizium Si:P Phosporous doped Silicon Phosphor dotiertes Silizium Gleichungen Konvektionsstromdichte für Elektronen: j = ¦ ρ* v ρ * = − qn Elektronen mit effektiver Masse, m* 1 We = me*ve2 2 W k p e = e* ⋅ e 2me k e me 0 = 9.109 × 10 −31 kg Ruhmasse im Vakuum Im Elektronengas gilt im thermischen Gleichgewicht ½ kBT pro Freiheitsgrad. Die thermische Geschwindigkeit im 3 dimensionalen Festkörper ergibt sich daher aus: 1 * 2 3 me vth = k BT 2 2 Für T=300K und m*=me0 ergibt sich vth=1.15×105ms-1. Die Bewegungsrichtungen der Elektronen sind statistisch ungeordnet und in jeder Richtung gleich wahrscheinlich. Daraus folgt: v =0 Am Kristallgitter werden die Elektronen gestreut (thermische Gitterstreuung). Die mittlere freie Flugzeit zwischen zwei Stößen ist durch τc charakterisiert die unabhängig von der kinetischen Energie sei. d v dt =− Stoß v τ mit τ = τ c Die Geschwindigkeitsänderung als Folge eines elektrischen Feldes, E läßt sich aus der Kraftgleichung bestimmen: d v dt = Feld −q E me* Daraus resultiert die gesamte Änderung der Geschwindigkeit: d v dt = d v + dt Stoß d v dt =− Feld v τ + −q E me* Im stationären Fall: d v dt v =0→ τ v = − µE, = µ= −q E me* q τ me* jdrift = − qn v = qnµ n E = σ n E Ladungstransport. Die Diffusion von Ladungsträgern entlang eines Konzentrationsgradienten ist proportional zum negativen Gradienten der Konzentration, also -Dn∇n. Aus dem Teilchenfluß folgt ein Ladungstransport: jdiff = qDn ∇n Driftbeweglichkeit, µn und Diffusionskonstante, Dn sind über die Einsteinrelation verknüpft: Dn = k BT µn q Der Konvektionsstrom durch Elektronen im Festkörper ergibt sich aus der Summe der einzelnen Komponenten: jn = jdrift + jdiff = q (nµ n E + Dn ∇n ) Welle – Teilchendualismus. De Broglie ordnet einem Wellenpaket der Wellenlänge λ einen Impuls zu: p = k 2π k= λ ∂ω vg = ∂k W = ω = hν Für das Teilchen gilt: mv 2 p 2 (mvTeilchen ) = = 2 2m 2m 2 W= Vergleich von Gruppengeschwindigkeit vg der Welle mit der Teilchengeschwindigkeit, vTeilchen: vg = ∂ω ∂W p = = = v Teilchen ∂k ∂p m Beispiele zur Heisenbergschen Unschärferelation: ∆p x ⋅ ∆x ≥ h, ∆W ⋅ ∆t ≥ h Schrödinger Gleichungen: Ψ ( x, y , z , t ) h2 2 h ∂Ψ ∇ Ψ + U ( x, y, z )Ψ = − 2m i ∂t 2m ∇ + 2 [W − U (x, y, z )]Ψ = 0 h − W = const 2 Ψ ..... Aufenthaltswahrscheinlichkeit h * Ψ ∇ΨdV = p i h ∂ * ∫V Ψ − i ∂t ΨdV = W ∫ V Das Elektron im periodischen 1D Gitter, V(x+l)=V(x) (Kronig-Penney Modell) illustrieren den Einfluß des Gitters auf die „freien“ Ladungsträger. d 2Ψ 2mW + α 2 Ψ = 0, α2 = 2 2 dx 2 2m(V0 − W ) d Ψ β2 = − β 2 Ψ = 0, 2 2 dx Ψ ( x ) = u ( x) exp(± ikx ) Die effektive Masse zur Beschreibung der Teilchenbewegung im periodischen Potential: dW = Fvdt = F 1 dW dt dk dk F = dt dv 1 d 2W dk = ⋅ dt 2 dk 2 dt dv F d 2W F = 2 ≡ * 2 dt dk m 2 m* = 2 d W dk 2 d 2W m* 2 = m* (1 + ......) dk Zum Loch (=Defektelektron) als beweglicher Ladungsträger mit einer positiven Elementarladung. Elektron Driftgeschwindigkeit v = −µ n E Loch v = +µ pE jdrift qnµ n E qpµ p E jdiff qDn ∇n − qD p ∇p jn = q(nµ n E + Dn ∇n ) j p = q ( pµ p E − D p ∇ p ) jTOTAL = jn + j p Besetzungswahrscheinlichkeit Fermi-Dirac-Statistik da Elektronen Fermionen sind. 1 f ( E,T ) = e ( E − EF ) k BT +1 EF ist die Fermienergie. Für E=EF gilt f(E)= ½ . In einem System im Gleichgewichtszustand gibt es nur ein Ferminiveau. Boltzmann-Näherung zur Ladungsträgerstatistik: f e ( E ,T ) ≅ e − ( E − EF ) k BT für ( E − E F ) > 3k BT f h ( E , T ) ≅ e −( EF − E ) k BT für ( E − E F ) < −3k BT Zustandsdichte: 1 2me* g c (E ) = 2π 2 2 1 2mh* g v (E ) = 2π 2 2 3 3 2 E − E LB für E > E LB 2 EVB − E für E < EVB Ladungsträgerdichte: 3 me* k BT 2 −( ELB − EF ) k BT e n = ∫ g c (E ) f e (E , T )dE = 2 2 ELB 2π ∞ 3 mh* k BT 2 +( EVB − EF ) k BT e ( ) ( ) p = ∫ g v E f h E , T dE = 2 2 −∞ 2 π * E + E LB 3 m E F = VB + k BT ln h* me 2 4 EVB 3 ( k T n ⋅ p = 4 B 2 me* mh* 2π ) 3 2 e − E g k BT = ni2 Die Äquivalente Zustandsdichte der Elektronen Nc und Löcher Nv ist per Definition: m* k T N c ≡ 2 e B 2π m* k T N v ≡ 2 h B 2π 3 3 2 2 ⇒ n = N c e −( ELB − EF ) k BT ⇒ p = N v e −( EF − EVB ) k BT n ⋅ p = N v N c × e −( ELB − EVB ) k BT = N v N c × e 3 ni (T ) ∝ T 2 e 5. −Wg k BT = ni2 −Wg 2 k BT Quellen P. Drude „Zur Elektronentheorie der Metalle“, Annalen der Physik. 306, Nr. 3, 566–613, 1900. [2] R. Müller, „Grundlagen der Halbleiter-Elektronik“, 3. Auflage, Berlin, Springer 1979. [1] S. Wei, M.Y. Chou, „Phonon dispersions of silicon and germanium from first-principles calculations“, Phys. Rev. B, 50, 2221 (1994) [4] W. C. Dash, and R. Newman, „Intrinsic Optical Absorption in Single-Crystal Germanium and Silicon at 77°K and 300°K“, Phys. Rev. 99, 1151 (1955) [3]