11. Phasenübergänge

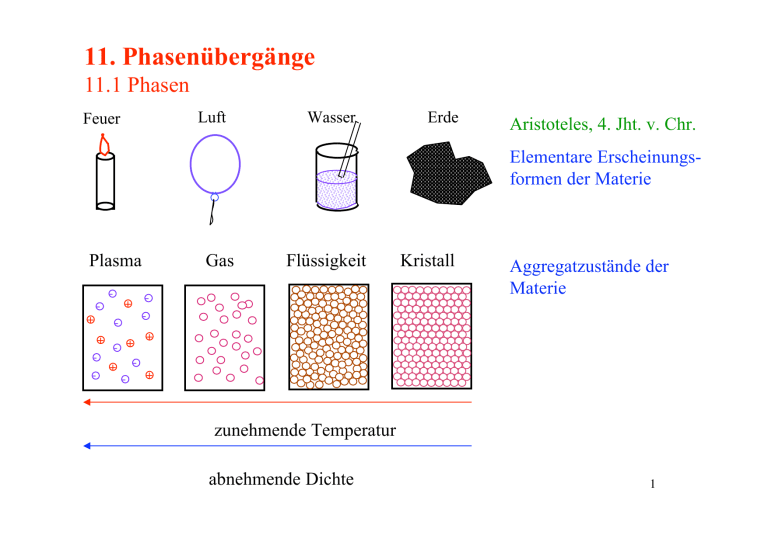
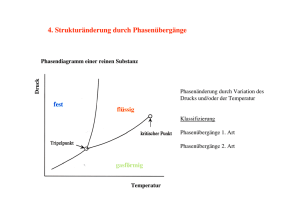
11. Phasenübergänge
11.1 Phasen
Luft
Feuer
Wasser
Erde
Aristoteles, 4. Jht. v. Chr.
Elementare Erscheinungsformen der Materie
Plasma
+
-
-
+
-
+
-
-
Gas
Flüssigkeit
-
Kristall
Aggregatzustände der
Materie
-
+
- +
+ +
-
zunehmende Temperatur
abnehmende Dichte
1
11.2 Unterschiedliche Phasen im festen Zustand
Amorpher
Festkörper
Magnetische
Ordnung
Kristall
Überstruktur
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
Elektrische
Ordnung
"quinta essentia"
Supraleiter
2
Ordnungsparameter
Charakterisierung der Phase durch eine Größe, Ordnungsparameter, die sie eindeutig
von allen anderen Phasen unterscheidet
Einige Beispiele
Phase
Ordnungsparameter
Flüssigkeit
Dichtedifferenz zum Gas
Kristall
Gittersymmetrie
Überstruktur
Anteil der richtig besetzten Gitterplätze
Ferromagnetische Ordnung
Spontane Magnetisierung
Supraleiter
Energielücke zum normalleitenden Zustand
Supraflüssigkeit
Dichte der suprafluiden Komponente
3
11.3 Existenzbereiche von Phasen
Unter welchen Bedingungen treten welche Phasen in welchen Stoffen auf?
Tc
Temperatur
Ising-Modell:
z
S = +1
S = -1
Eges = ∑ J i, j Si S j
i, j
Tc = J /(kB tanh( 2 −1))
Ferromagnet
Paramagnet
€
4
11.4 Materialkonstanten kondensierter Materie
Feldgrößen: Druck P, Temperatur T, elektrisches Feld E, magnetisches Feld B,
intensive Größen
Thermodynamisch konjugierte Mengengrößen: Volumen V, Entropie S, elektrisches
Dipolmoment me, magnetisches Dipolmoment mm,
extensive Größen
Produkt aus Feldgröße und Mengengröße ergibt eine Energie.
Thermodynamisches Potential Φ:
:
Φ = E + V · P + S · T + me · E + mm·B
Statische Materialkonstanten:
χ
( XY )
∂X
=
∂Y
X: Mengengröße
Y: Feldgröße
χ: verallgemeinerte Suszeptibilität
5
€
Intensive Feldgrößen
€
€
€
€
Extensive Feldgrößen
mm (Am2) me(Asm) V (m3) S ((J/K)
Y
X
T(K)
Wärmekapazität
χ (ST ) =
∂S
∂T
Wärmeausdehnung
P (N/m2)
Piezokalorischer
Effekt
χ (SP ) =
∂S
∂P
Kompressibilität
E (V/m)
B (Vs/m2)
Elektrokalorischer MagnetokaloriEffekt
scher Effekt
χ (SE ) =
∂S
∂E
Elektrostriktion
χ (SB ) =
∂S
∂B
Magnetostriktion
∂V
χ (VT ) =
∂T
€
Pyroelektrischer
∂V
χ (VP ) =
∂P
€
Piezoelektrischer
∂V
χ (VE ) =
∂E
€
Elektrische
Effekt
Effekt
Polarisierbarkeit
Magneto-elektrischer Effekt
Pyromagnetischer Effekt
Piezomagnetischer Effekt
scher Effekt
barkeit
∂m
χ (meT ) = e
€ ∂T
∂m
χ (me P ) = e
€ ∂P
€
∂V
∂B
∂m
∂m
χ (me E ) = e χ (me B ) = e
∂E
∂B
€
Elektro-magneti- Magnetisier-
∂m
∂m
∂m
χ (mmT ) = m χ (mm P ) = m χ (mm E ) = m
€ ∂T
€ ∂P
€ ∂E
€
χ (VB ) =
€
χ (mm B ) =
∂mm
∂B
6
11.5 Transportkoeffizienten
Materie nicht im thermodynamischen Gleichgewicht
 Entstehung von Flüssen (Masse, Energie, Impuls, elektr. Ladung, etc.)
Transportgleichungen:
JX: Fluß (Stromdichte) = (∂X/∂t)/A
FY: treibende Kraft
= grad Y
LXY: Transportkoeffizienten
JX = LXY FY
Reservoir 1
Y(1)
JX
A
z
Reservoir 2
Y(2)
7
Treibende Kraft
Fluß (Stromdichte)
JX
FY
JQ
(J/m2s)
grad T
(K/m)
Wärmeleitung
Thermomech-
Jm anischer
(kg/m2s) Effekt
JN
(m-2s-1)
Jq
(A/m2)
Soret-Effekt
grad P
(kg/m2s2)
grad c
(m-4)
Mechanokal- Diffusionsrischer Effekt Wärme
(Dufour)
grad U
(V/m)
PeltierEffekt
MasseTransport
Diffusion
ElektrizitätsLeitung
8
€
11.6 Flüssigkeiten
Gas
E=0
η= 10-5 kg/(ms)
K ≈ 1 / bar
τ ≈ 10-10 s
Flüssigkeit
Festkörper
E≈0
η = 10-3 kg/(ms)
K ≈ 10-9 / bar
τ ≈ 10-8 s
E = 1011 N/m2
η∞
K ≈ 10-10 / bar
τ  ∞ (T=0)
Atomare Wechselwirkung (Lennard-Jones-Potential):
 12  6 
σ
σ 

U (r ) = 4ε   −  
 r   r  
Anziehender Term (Coulomb-WW)
Abstoßender Term (Pauli-Prinzip)
9
Beschreibung der Nahordnung durch Korrelationsfunktionen
g(r,t ) = g s (r,t ) + g p (r,t )
Paarkorrelationsfunktion
Selbstkorrelationsfunktion
Energie:
€
f
N2
E = NkB T +
2
2V
∫ U (r ) g
2
(r
)
4
π
r
dr
p
V
Potentielle Energie
Kinetische Energie
€
Suszeptibilität:
 ∂E 
f
N2
CV =   = NkB +
2V
 ∂T V 2
 ∂g p 
∫ U (r ) ∂T  4πr 2 dr


V
10
Paarkorrelationsfunktion
einer Flüssigkeit und Nahordnung
Transportkoeffizienten
dynamische Vorgänge 
Zeitabhängigkeit der Korrelationsfunktion
Brown’sche Bewegung der Atome
Selbstkorrelationsfunktion gs(r,t)
 r2 
g s (r,t ) =
exp −

3/2
N
4D
⋅
t


4π ⋅ D ⋅ t )
(
V
1
Mittleres Abstandsquadrat:
€
r
N
=
V
∞
2
2
r
g
(r,t
)
4
π
r
dr
∫ s
0
Diffusionskoeffizient D:
〉
€
2
r2〉 = 6D·t
1 2
D= ν ⋅L
6
Platzwechselfrequenz ν
Energieschwelle ∆ε
Sprungweite L
11
11.7 Wärmekapazität
Konstantes Volumen dV=0:
 dE 
CV =  
 dT V
Experiment: konstanter Druck dP=0: Umrechnung
CP = CV + 9α 2p VT / κ T
Verschiedene Beiträge:
ges
G
E
P
C =C +C +C =
E
∂E G
∂E P
∂E
+
+ €
∂T
∂T
∂T
) (
( ) (
)
Phononen kooperativer Anteil
Elektronen
CV
Spezifische Wärme
von Eisen
Fe
Gitteranteil
α
γ
γ
Elektronenanteil Ferromagnetische
Umwandlung
0
300
600
900
1200
δ
Schmelzen
1500
T (K)
1800
12
11.8 Änderungen der spezifischen Wärme bei Umwandlungen
Kooperative Anteile treten bei Phasenübergängen auf.
G
Freie Enthalpie:
G
G = H - TS = E - PV - TS
 ∂G 
 ∂G 
= −S;   = −V ;
 
 ∂T  P
 ∂P T
 ∂ 2G 
 ∂S 
 2  = −  =
 ∂T  P
 ∂T  P
1  ∂H 
CP
  =
T  ∂T  P T
S
S
∆S
CP
∞
Tu
1. Ordnung
CP
T
∞
Tc
2. Ordnung
T
€
13
11.9 Klassifizierung der Phasenübergänge
Klassifizierung nach Phasenübergängen 1. und 2. Art und höherer Ordnung
Beispiele:
1. Art
2. Art
Kristallisation
Kondensation
Sublimation
Martensitische Umwandlung
Ordnung-Unordnung (A3B)
Bildung von Domänen
(Ferroelektrika, Ferromagnete,
Flußgitter in Supraleitern 2. Art
Ferroelektrizität
Ferromagnetismus
Supraleitung
Superfluidität
Ordnung-Unordnung (AB)
Umwandlungen am kritischen Punkt
14
11.10 Phasenübergänge 1. Art
Charakterisierung durch: Keimbildung
Latente Wärme
Hysterese Effekte
Keimbildung:
Bildung von Clustern der
Tochterphase 2 in der
Mutterphase 1
 Energiegewinn
Aufbau einer Grenzfläche
 Energieaufwand
Phase 1
Phase 2
15
Bei der Übergangstemperatur stehen beide Phasen miteinander im Gleichgewicht
T = TE  G1(PE,TE) = G2(PE,TE)
Entwicklung der freien Enthalpie um TE:
∂G1
∂G1
∂G 2
∂G 2
2
G (PE ,TE ) + dP
+ dT
....... = G (PE ,TE ) + dP
+ dT
.......
∂P
∂T
∂P
∂T
1
Clausius-Clapeyron
€
€
1
2
∂G ∂G
−
1
2
dP ∂T
S
−
S
∂T =
=
dT ∂G1 ∂G2 V 1 − V 2
−
∂P ∂P
Entropiesprung,
Volumensprung
beide Phasen besitzen unterschiedliche
Eigenschaften am Übergangspunkt (PE,TE)
16
Phasenübergänge 1. Ordnung
• Sprünge in den extensiven Größen am Phasenübergang
• Behinderung des Anwachsens der Fluktuationen
• Existenz einer Aktivierungsschwelle für die Keimbildung
• Unterkühlung - Überhitzung
Beispiel: Verdampfen einer Flüssigkeit
VDampf >> VFlüssigkeit, ∆V ≠ 0, Verdampfungswärme
Phasenübergänge 1. Ordnung:
Schmelzen eines Festkörpers
Kristallisation einer Schmelze
Strukturelle Umwandlungen in Festkörpern
17
Aufbau einer Grenzfläche zwischen zwei verschiedenen Phasen erfordert Energie:
• Existenz einer Aktivierungsschwelle zur Keimbildung
• Kompensation durch Erniedrigung der freien Enthalpie
Energiebilanz während der Keimbildung:
ΔG =
4π 3
R ⋅ ΔGV − 4π R2 ⋅ σ
3
Volumenterm
€
Volumen- und Grenzflächenterm
haben unterschiedliche Abhängigkeit
vom Keimradius  ∆G durchläuft
ein Maximum bei der
Energieschwelle ∆G* und beim
kritischen Keimradius R*!
Grenzflächenterm
∆GV = G2 - G1 < 0 (T < TE): Enthalpiegewinn
σ > 0: Energieaufwand durch Grenzfläche
∆G
Energieschwelle ∆G* zur Aktivierung
wachstumsfähiger Keime:
ΔG * =
16π σ
4ΔGV
3
4πR2σ
∆G*
R*
R
4/3 πR3∆Gv
18
€
Reaktionskinetik, Phasengleichgewicht flüssig-fest
Zufuhr der Schmelzenthalpie kontrolliert das Schmelzen einer Substanz:
Geschwindigkeiten der Teilreaktionen: RM: Schmelzen, RF: Erstarren
Anzahl der an der Reaktion beteiligten Atome
Akkomodationskoeffizienten
Geometriefaktoren
Schwingungsfrequenzen
Aktivierungsenergien
Gaskonstante
24
12
0
0
kfz/ hdp
∆Sf≈20,4 J/mol K
F2, Cl2
400
krz
∆Sf≈8,5 J/mol K
800
1200
1600
Schmelztemperatur [K]
∆Hf = ∆Sf·TE
2000
ΔH f
AM
≈ ln F
RTE
A
RM
Cu
2400
1800
1200
TE(Cu)
RF
600
T = T E: R F = R M
Ebene Grenzfläche:
G M = GF
Metalle:
N S ≈ NL
vS ≈ v L
kovalente Strukturen
∆Sf≈ 15 J/mol K
36
3000
500
1000
1500
2000
Temperatur (K)
Energie
Schmelzenthalpie [kJ/mol]
NL,S:
AM,F:
GM,F:
vS,L:
QM,F:
R:
RM, RF (cm/s)
3600
RM = NS·AM ·GM ·vS ·exp(-QM/RT)
RF = NL·AF ·GF ·vL ·exp(-QF/RT)
QF
QM
∆Hf
∆Hf = QM - QF
19
11.11 Phasenübergänge 2. Art
T = Tc  ∆S = 0, ∆V = 0
Tc: kritische Temperatur
Beide Phasen besitzen gleiche Eigenschaften am kritischen Punkt.
Erste Ableitung der freien Enthalpie zeigt keinen Sprung
bei Tc, sondern verläuft stetig.
Extensive Größen beider Phasen am kritischen Punkt werden gleich
Keine Grenzflächenenergie zwischen beiden Phasen
Keine Aktivierungsschwelle zur Keimbildung
Keine latente Wärme
Fluktuationen des Ordnunsgparameters werden bei Annäherung an die kritische
Temperatur sehr groß;
Schwankungen durch Brown’sche Wärmebewegung der Atome (Molekühle)
T  Tc: Zunahme der Reichweite und Abnahme der Relaxationszeiten
der Fluktuationen, dies gilt bei Annäherung an den kritischen Punkt
von hohen und tiefen Temperaturen.
20
Kritische Fluktuationen
T >> Tc
Reduzierte Temperatur:
Korrelationslänge:
Lebensdauer:
Tr = |T -Tc|/Tc
ξ
τ
10-5 - 10-2
(1000 - 10) nm
(10-10 - 10-11) s
T > Tc
ξ
 T − T −2 / 3
c

ξ ∝ 

 Tc 
 T − T −1/ 3
c

τ ∝ 

 Tc 
τ
Korrelationslänge
(mittlerer Radius)
T ≈ Tc
€
Lebensdauer
€
Tc
T
Tc
T
Helle Quadrate: Spin oben
Dunkle Quadrate: Spin unten
21
Kritische Exponenten
Experiment:
T ≥ T c:
χ≈ (T - Tc)-1,41
γ= -1,41
Gleichbeschaffenheit beider Phasen am kritischen Punkt
Verhalten thermodynamischer Eigenschaften bei Tc:
A(Y ) = Ao
€
Y − Yc
Yc
z
A:
Y:
Yc:
z:
Eigenschaft
Feldgröße (T,P,B,E)
kritischer Wert der Feldgröße
kritischer Exponent
z > 0: A  0 für Y  Yc
z < 0: A  ∞ für Y  Yc
z = 0: logarithmische Divergenz
Deutung durch Renormierungstheorie
Nobelpreis 1982: K. G. Wilson
Gültigkeitsbereich:
10-5 < Tr < 10-2
Atomabstand << Korrelationslänge
<< Probenabmessungen
:
Theorie:
γ = -1,39
100
Ni
χ
10
,
1,0
0,1
0,01
10-5
10-4
10-3
10-2
Tr
22
Universalität von Phasenübergängen 2. Ordnung
Symmetrie des Ordnungsparameters:
Anzahl n seiner wechselwirkenden Komponenten, n: “Spindimension”
n = 1: Ising Modell
n = 2: XY - Modell
n = 3: Heisenberg - Modell
Bedingung: kurzreichweitige Kräfte
Wechselwirkungsenergie < kBT
Reichweite << Korrelationslänge
Universalität: Gleiche kritische Exponenten für unterschiedliche Phasenübergänge
Beispiele:
z < 0: Kompressibilität eines FlüssigkeitsGas-Systems, Tc: kritischer Punkt
Magnetische Suszeptibilität eines
Ferromagneten, Tc: Curie-Temperatur
z > 0: Energielücke für Cooper-Paare
in supraflüssigem 3He, Tc: Lambda-Punkt
Untergittermagnetisierung des antiferroMagnetischen NiO, Tc: Néel-Temperatur
Allein die geometrischen Eigenschaften der Fluktuationen bestimmen die makroskopischen Eigenschaften der Materie in der Nähe kritischer Punkte, unabhängig
23
von der Art der Wechselwirkung zwischen den Atomen!