Kristallstruktur und Mikrostruktur Teil II

Kristallstruktur und Mikrostruktur
Teil II
Teil II (Übersicht)
1 Erstarrung/ Grundlagen
2 Erstarrung/ Gefüge (Mikrostruktur)
3 Praktische Aspekte: Schweißen; Thermisches Spritzen
4 Texturanalyse
Macherauch 1989
2
Vorlesung 1 (Übersicht)
Phasendiagramme
Phasenübergänge und Klassifikation
Struktur von Schmelzen (ungeordneten Materialien)
Erstarrung
Erstarrungsvorgänge
Homogene Keimbildung
Heterogene Keimbildung
Literatur
3
Definition Phase
Eine Phase ist ein Zustand der Materie, in dem sie, bezüglich ihrer chemischen
Zusammensetzung und bezüglich ihres physikalischen Zustandes, durch und durch
homogen ist.
‚On the Equilibrium of Heterogeneous Substances‘, 1875-1876
Gibbssche Phasenregel
P=C–F+2
Gl. 1
P - Anzahl von Phasen
F – Anzahl von Freiheitsgraden (Zustandvariablen)
C - Anzahl der unabhängigen Teilchensorten
J.W. Gibbs 1839 - 1903
4
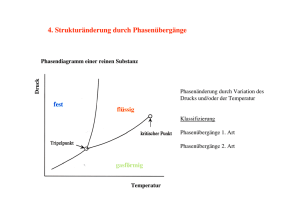
Phasendiagramme
Ein Phasendiagramm gibt an, welche Phase
eines Stoffes bei einer bestimmten Temperatur
und bei einem bestimmten Druck stabil ist.
Klassifikation nach der Zahl von Teilchensorten (C)
Unary (C = 1)
Binary (C = 2)
Ternary (C = 3)
5
Phasendiagramme
idealisiertes unary Phasendiagramm
Verdampfung (Übergang von flüssig zu gasförmig)
Sublimation (Übergang von fest zu gasförmig)
Erstarrung (Übergang von flüssig zu fest)
Kondensation (Übergang von gasförmig zu flüssig)
6
Unary Phasendiagramme - Beispiele
Xenon
T < 300 K
T > 310 K
7
Unary Phasendiagramme - Beispiele
Wasser
Phase Dichte Raumgruppe
(g/cm3)
Ih
0.92
P63/mmc
Ic
0.93
Fd-3m
II
1.195
R -3
VIII
1.885
I 41/amd
8
Binäre Phasendiagramme - Beispiele
C = 2 (zwei Komponenten)
2 Elemente
TE ~ 221 oC
9
Binäre Phasendiagramme - Beispiele
C = 2 (zwei Komponenten)
2 Verbindungen (Oxide)
Na2O
SiO2
10
Binary Phasendiagramme - Beispiele
C = 2 (zwei Komponenten)
1 Element + 1 Verbindung
a (Ferrite) bcc
g (Austenite) fcc
11
Ternäre Phasendiagramme - Beispiel
C=3
Fo – Forsterit Mg2SiO4
An – Anorthit CaAl2Si2O8
12
Phasenübergänge
Die Umwandlung einer Phase eines Stoffes in eine andere Phase ist
Phasenübergang (bzw. eine Phasenumwandlung oder
Phasentransformation) genannt.
Klassifikationen
Strukturelle
Thermodynamische
Kinetische
13
Strukturelle Klassifikation
von Phasenübergängen
Diskontinuierliche
Graphit → Diamant
NaCl → CsCl-Typ
hcp → fcc, fcc → hcp
Martensitische
Athermale
Isothermale
NiTi
Fe-Mn, Fe-Ni, Stahl
Kontinuierliche
Dizplazive
Ordnung-Unordnung
ß-Quarz → α-Quarz
AuCu
14
Strukturelle Klassifikation
von Phasenübergängen
Rekonstruktive
P 63/mmc
Fd3m
Änderung der Koodinationzahl (CN 3 → 4)
15
Strukturelle Klassifikation
von Phasenübergängen
Martensitische
P m -3 m
P 1 21/m 1
16
Strukturelle Klassifikation
von Phasenübergängen
Displazive
Raumgruppe
P 31 21
Raumgruppe
P 62 2
Die ersten Koordinationen von Si und O bleiben dieselben, nur
kleine Rotationen der Tetrahedra (SiO4) findet statt.
17
Kinetische Klassifikation
von Phasenübergängen
Nullte Ordnung
Ṙ ist konstant
Erste Ordnung
Ṙ = Ṙ (Konzentration der Ausgangsphase)
Zweite Ordnung
Ṙ = Ṙ (Konzentrationen von zwei AusgangsSubstanzen)
Ṙ - Reaktionsrate
18
Thermodynamische Klassifikation
(Ehrenfest Klassifikation)
Gibbssche Energie
G = H – pV – ST
Gl. 2
S = - ∂G/∂T│P
Gl. 3a
V = - ∂G/∂p│T
Gl. 3b
Paul Ehrenfest
(1880 – 1933)
19
Thermodynamische Klassifikation
(Ehrenfest Klassifikation)
1. Ordnung
Die ersten Ableitungen der
Gibbsschen Energie zeigen
Sprünge.
2. Ordnung
Die ersten Ableitungen der
Gibbsschen Energie zeigen
keine Sprünge.
Die zweiten Ableitungen
zeigen Diskontinuitäten.
20
Thermodynamische Klassifikation
(Ehrenfest Klassifikation)
21
Thermodynamische Klassifikation
(Ehrenfest Klassifikation)
1. Ordnung
Erstarren
(Kristallization)
Kondensation
Sublimation
Martensitische Umwandlungen
2. Ordnung
Ferroelektrizität
Ferromagnetismus
Supraleitung
_______________________________________________________________
Keimbildung
Keimbildung
Aktivierungsschwelle für die
Keimbildung
keine Aktivierungsschwelle für Keimbildung
Latente Wärme l = T(S1 – S2)
keine latente Wärme
22
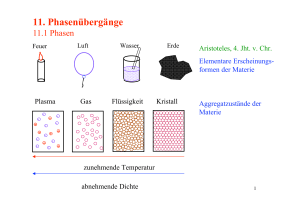
Ungeordnete (Amorphe) Stoffe
Phasenübergäng Flüssig → Fest
Festzustand
Kristalline Stoffe
Quasikristalle
Nicht-kristall. Festkörper
Flüssigzustand
Flüssigkeiten
Schmelzen
TS – Translationssymmetrie
LRO – Fernordnung
MRO – Mittelreichweitige Ordnung
SRO - Nahreichweitige Ordnung
Stoffe
TS
LRO
MRO
SRO
Kristalline
√
√
√
√
√
√
√
√
√
Quasikrist.
Amorphe
23
Struktur von ungeordneten Materialien
24
Atomare Teilchendichte
2
●
3
●
1
●
●4
5
●
ri = (xi yi zi)
r(r) = Σ d(r – ri)
Gl. 5
25
Paarkorrelationsfunktion g(r)
g(r) = (r(r)/ro)4pr2dr
Gl. 6a
ro = N/V mittlere Dichte des Stoffes
g(r) hat zentrale Bedeutung für die Beschreibung von Flüssigkeiten und
amorphen Festkörper.
g(r) = 1 + (1/4pror)2/p ∫ Q [S(Q) – 1]sin(Qr)dQ
6b
Q = 4p/l sin(Q)
Beugung
26
Paarkorrelationsfunktion - Beispiele
Gas
r/DA
DA
27
Paarkorrelationsfunktion - Beispiele
Liquid Ar
A. Leach (2001)
r → ∞ g(r) → 1
28
Paarkorrelationsfunktion - Beispiele
Leach (2001)
29
Phasenübergang Flüssig → Fest
(Erstarrung)
Thermodynamische Bedingung
GFK < GL
Amorphisation
bei
T < Tm
G
Kristallisation
GL
GFK
Abkühlen
‚langsam‘
‚schnell‘
Zustand
Kristalle (kristalline Festkörper)
Gläser (amorphe Festkörper)
T
Tm
30
Phasenselektion/Unterkühlungsgrad
Abkühlrate
und/oder
Unterkühlungsgrad
rasches Abkühlen
Glas
31
Glasübergangstemperatur
① Unterkühlte Schmelze
Tg Glasübergangstemperatur
Rössler (2000)
Festkörper
(Glas oder Kristall)
①
Schmelze
32
Glasübergangstemperatur
33
Struktur von unterkühlten Schmelzen
US –untrekühlte Schmelze
S - Schmelze
US
S
US
S
Holland-Moritz (2002)
34
Struktur von unterkühlten Schmelzen
Na2O.4SiO2 Glas und
unterkühlte Schmelzen
Neutronenbeugung
Zotov (2000)
Q = 4p/l sin(Q)
Struktur der Schmelze ≈ Struktur der unterkühlten Schmelze ≈ Glasstruktur
35
Struktur von unterkühlten Schmelzen
(Clusterbildung in metallischen Schmelzen)
Dynamische Prozesse!
Diffusion
Bindung von Atomen (b) (c)
Atom Attachment/Abtrennung (e) (f) (g) → Clusterbildung
fcc
pentagonale
Dipyramide
Icosahedron
Gerlach et al. (2006)
Cluster sind unterkritische (instabile) Keime
36
Struktur von unterkühlten Schmelzen
(Clusterbildung in metallischen Schmelzen)
Verteilung von kugelförmigen Clustern in der (unterkühlten) Schmelze mit Radius r
n(r) - Anzahl von Clustern mit Radius r:
n(r) = no exp(-DGr/KT),
n
wo DGr = GL – GC(r) > 0
Große Cluster nicht stabil
Abtrennen bevorzugt
Zerfall von Clustern
Attachment bevorzugt
Bildung von Clustern
Anzahl von Atomen
im Cluster
37
Keimbildung
Homogene Keimbildung
alle Stellen sind gleichberechtigt
Heterogene Keimbildung
Keimbildung findet bevorzugt an Grenzflächen
(Wände; Rissen, Fremdkörper, etc.) statt.
L
ß
38
Erstarrungsvorgänge
Klassifikation nach Konzentrationsänderungen
Erstarrung ohne Konzentrationsänderungen
(z.B. bei reinen Metallen oder bei kongruent-schmelzenden
intermetallischen Verbindungen)
Erstarrung mit Konzentrationsunterschied zwischen der Schmelze (a) und
der erstarrten Phase (ß)
Erstarrung mit der Bildung von zwei Phasen unterschiedlicher Zusammensetzung
39
Klassisches Keimbildungsmodel
homogene Keimbildung ohne Konzentrationsänderungen
Spezifische Gibbs-Energie (per Volumeneinheit)
GL
=
HL
–
TSL
GS = HS – TSS
(Gibbs-Energie der Schmelze)
Bei T = Tm die Schmelze und der Kristall
sind im Gleichgewicht:
(Gibbs-Energie des Festkörpers)
DGV│Tm = 0
DGV= GL – GS = DH – TDS
(‚treibende‘ Kraft der Erstarrung)
oder
DGV = DG│Tm + ∂∆G/∂T │Tm (T-Tm) + ∙∙ ≈
≈ DG│Tm + DS│Tm DT
DGV ≈ LDT/Tm
Gl. 8a
Gl. 7
Gl. 10
DS│Tm = DH/Tm
Gl. 8b
Erstarrung ist ein Phasenübergang 1. Ordnung
DH ~ L (Latentwärme)
DS│Tm ~ L/Tm
Gl. 9
(Schmelzentropy)
Richard‘s Regel DS│Tm ~ R (8.3 J/mol.K)
40
Klassisches Keimbildungsmodel
Gottstein (2001)
41
Klassisches Keimbildungsmodel
homogene Keimbildung ohne Konzentrationsänderungen
DGhom = -VS DGV + ASLgSL
Gl.11
Embryos
Für kugelförmigen Embryo mit Radius r:
DGhom = -4/3 p r3 DGv + 4pr2 gSL
Keime
Gl. 12
gSL - Grenzflächenenergie Solid-Liquid (J/m2)
ASL – Solid-Liquid Fläche
r < r*
instabile Keime (Embryos)
r > r*
stabile Keime
42
Klassisches Keimbildungsmodel
homogene Keimbildung ohne Konzentrationsänderungen
Der kritische Radius r* und die kritische Energie (Widerstand gegen Keimbildung) DG*
Die Größe des kritischen Radius r* folgt von der Bedingung:
∂DG/∂r = 0 → r* = 2gSL/DGv
Gl. 13
r* = (2gSL/L) Tm/DT
Gl .14
DG*hom = (16 p gSL3 Tm2/3L2) 1/(DT)2
Gl. 15
43
Klassisches Keimbildungsmodel
homogene Keimbildung ohne Konzentrationsänderungen
Keimbildungsrate
Ṅhom = No exp(-DG*hom/kT) =
= No exp (- A/(DT)2 );
A = 16 p gSL3 Tm2/3L2kT
Gl. 16
DTN – kritische Unterkühlung für
homogene Keimbildung
DTN~ 0.2 TM (die Turnbull-Regel)
44
Klassisches Keimbildungsmodel
heterogene Keimbildung ohne Konzentrationsänderungen
1 die Minimisierung der gesamten Grenzflächenenergie führt zu
Der Winkel (ABC) = 2Q
gML = gSM + gSL cos(Q)
(gSL ist isotrop)
Gl. 17
gML die Grenzflächenenergie Mould-Schmelze
gSM die Grenzflächenenergie Solid-Mould
gSL die Grenzflächenenergie Solid-Liquid
Q der Benetzungswinkel
2 Änderung der Gibbsschen Energie:
DGhet = -VS DGV + ASLgSL + ASMgSM – ASMgML =
= -VS DGV + ASLgSL – ASMgSLcos(Q)
C
A
2Q
B
45
Klassisches Keimbildungsmodel
heterogene Keimbildung ohne Konzentrationsänderungen
DGhet = {-4/3 p r3 DGv + 4pr2 gSL } S(Q) =
= DGhom S(Q)
S(Q) = (2 + cosQ)(1 – cosQ)2/4
Gl. 18a
Q = 10o S(Q) = 10-4
Q = 30o S(Q) = 0.02
Q = 90o S(Q) = 0.5
Gl. 18b
Reduzierung der Energiebarriere für Keimbildung
DG*het = DGhom * S(Q)
46
Klassisches Keimbildungsmodel
heterogene Keimbildung ohne Konzentrationsänderungen
Heterogene Keimbildung:
niedrige kritische Energiebarriere DG*
kleinere kritische Unterkühlung DTN
47
Literatur
Hauptquellen
K. E. Estarling
Introduction to the physical metallurgy of welding, 1992
D.V. Potter, K.E. Easterling, M.Y. Sherif
Phase Transitions in Metals and Alloys
CRC Press, 2009
G. Gottstein
Physikalische Grundlagen der Materialkunde
Springer, 2001
E.J.Mittemeijer
Fundamental of Material Science, 2010
48
Übungen
Übungen_WS_2016/2017
Name
Vorname
BE
VG
Zaverkin
Viktor
BE
2
Kluck
Sebastian
BE
2
Pfeiffer
Robin
BE
2
Schilling
Alexander
BE
1
Müller
Henry
BE
1
Duda
Sebastian
BE
1
Aulich
Marc
BE
1
Steinle
Laura
BE
1
Kaeswurm
Louise
BE
1
Jennerjahn
Ina
BE
2
Rosenmayer
Sandra
NB
0
Schilling
Fiona
BE
2
Lindner
Laura
BE
1
Brendle
Alexander
BE
2
Peter
Claudia
BE
1
Güney
Okan
BE
1
Didem
Cansu Cetin
BE
2
Melek
Aygün
BE
1
Hojczyk-Rubio
Camilla
BE
0
Kim
Joonhwan
BE
1
Tauber
Felix
BE
1
Kutlu
Aycan
BE
1
Hotz
Daniel
BE
1
Hildenbrand
Kevin
BE
1
Theis
Lukas
BE
1
Zhang
Kun
BE
1
Schäfer
Robin
BE
1
Kappler
Julian
NB
0
Unseld
Jan
BE
3
Wurster
Ralf
BE
1
Bernath
Daniel
NB
0
49