TM1-Klausur WS 2006/07 - Department Fahrzeugtechnik und

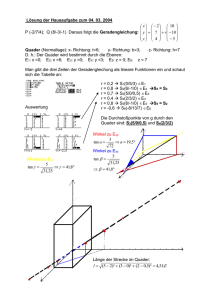
Hochschule für Angewandte Wissenschaften Hamburg
Department Fahrzeugtechnik und Flugzeugbau
Prof. Dr.-Ing. R. Ahrens
Prüfungsklausur Statik / Technische Mechanik I
WS 2006/2007
Statik / Technische Mechanik I
Prüfungsklausur WS 2006/2007
29.01.2007
Name:
____________________
Vorname: ____________________
Matr.-Nr.: ____________________
Aufgabe
1
2
3
4
5
6
Σ
Maximale Punktzahl
10
10
8
11
10
11
60
Erreichte Punktzahl
Bearbeitungszeit:
Hilfsmittel:
Note: ___________
180 min.
Alle eigenen Unterlagen; Taschenrechner.
Hinweise:
•
•
•
•
•
•
•
•
•
•
Trennen Sie bitte zu Beginn dieses Deckblatt ab und legen Sie es ausgefüllt zusammen mit Ihrem
Studentenausweis und einem Lichtbildausweis gut sichtbar auf Ihrem Tisch bereit.
Lesen Sie zunächst alle Aufgaben genau durch; beginnen Sie dann mit der Aufgabe, die Ihnen am
sympathischsten erscheint.
Beschreiben Sie bitte die Blätter nur einseitig.
Beginnen Sie jede Aufgabe auf einem neuen Blatt.
Schreiben Sie auf jedes Blatt Ihren Namen und Ihre Matrikelnummer.
Verwenden Sie bitte keinen Bleistift (außer in Zeichnungen).
Verwenden Sie bitte keinen roten Stift (außer in Zeichnungen).
Machen Sie bitte eindeutig kenntlich, was nicht gewertet werden soll; falls die Bearbeitung
mehrere sich widersprechende Lösungen zu einem Aufgabenteil enthält, muss dieser Teil ansonsten als falsch bewertet werden.
Geben Sie mindestens das ausgefüllte Deckblatt ab.
Die Aufgabenblätter dürfen Sie behalten; falls die Aufgabenblätter Notizen bzw. Lösungsanteile
enthalten, geben Sie sie bitte mit ab.
Viel Erfolg!
1
Hochschule für Angewandte Wissenschaften Hamburg
Department Fahrzeugtechnik und Flugzeugbau
Prof. Dr.-Ing. R. Ahrens
Prüfungsklausur Statik / Technische Mechanik I
Aufgabe 1:
WS 2006/2007
(ca. 10 Punkte)
Auf das skizzierte Gestell mit Rolle (Radius R) wirkt über das Seil S
die Gewichtskraft G. Alle Systemteile sind masselos, die Gelenke A,
B, C und E sind reibungsfrei.
·
Bestimmen Sie die Auflagerreaktionen in A und B sowie die Kraft im
Gelenk C.
Gegeben: G, a, b, R, α = 60°.
Aufgabe 2:
(ca. 10 Punkte)
Das dargestellte ebene Fachwerk mit masselosen
Stäben und reibungsfreien Gelenken ist wie skizziert in den Punkten C und D jeweils durch eine
Kraft P belastet.
Bestimmen Sie:
a) die Kräfte in den Stäben 6, 7 und 8;
b) die Kräfte in den Stäben 9, 10 und 11.
Gegeben: P, a.
Aufgabe 3:
(ca. 8 Punkte)
Das dargestellte Uhrenpendel besteht aus der Pendelstange 1 (Quader
der Länge ℓ, Breite b und Dicke t, Dichte ρ1) sowie der Schwungmasse 2 (Kreisscheibe mit Radius r und Dicke t2=2t Dichte ρ2), die eine
Aussparung für die Pendelstange enthält.
Bestimmen Sie die z-Koordinate des Gesamtschwerpunktes des Uhrenpendels im angegebenen Koordinatensystem.
Gegeben: ℓ=30cm, r=5cm, b=2cm, t=1cm, t2=2cm,
ρ1=6g/cm³, ρ2=9g/cm³.
2
Hochschule für Angewandte Wissenschaften Hamburg
Department Fahrzeugtechnik und Flugzeugbau
Prof. Dr.-Ing. R. Ahrens
Prüfungsklausur Statik / Technische Mechanik I
Aufgabe 4:
WS 2006/2007
(ca. 11 Punkte)
Die skizzierte Straßenlaterne besteht aus einem senkrecht
stehenden Mast (Höhe h) und einem horizontalen Ausleger
(Länge ℓ), die im Punkt B fest miteinander verbunden sind
(biegesteife Ecke). Der Mast ist im Punkt A gelenkig gelagert (dreiwertiges Lager) und wird im Punkt B durch zwei
Seile gehalten, deren Befestigungspunkte den Abstand 2b
voneinander haben und um den Betrag a hinter dem Punkt B
sowie um den Betrag c oberhalb des Punktes B liegen. Am
Ende des Auslegers, der in die positive x-Richtung weist,
wirkt die Gewichtskraft G der Lampe in vertikaler Richtung;
Mast und Ausleger sind masselos.
Bestimmen Sie die Lagerreaktionen in A und die Seilkräfte.
Gegeben: G, a=2m, b=3m, c=1m, h=6m, ℓ=4m.
Aufgabe 5:
(ca. 10 Punkte)
Ein Quader (Masse m2) soll durch eine Kraft F mit konstanter Geschwindigkeit v über eine horizontale Ebene
gezogen werden. Auf den Quader drückt eine Klappe
(Masse m1, Länge = ℓ, Schwerpunkt S1). Zwischen
Klappe und Quader herrscht der Reibungskoeffizient µ1,
zwischen Quader und Untergrund der Reibungskoeffizient µ2.
a) Wie groß muss die Kraft F sein (als Funktion des Winkels α)?
b) Wie groß muss der Winkel α mindestens sein, damit keine Selbsthemmung (F → ∞) eintritt?
Gegeben: m1, m2, µ1, µ2, ℓ;
Aufgabe 6:
α (nur für a).
(ca. 11 Punkte)
Ein Balken der Länge 2ℓ ist wie skizziert in D
gelenkig gelagert und über ein horizontales Seil
S abgespannt. Ausleger BC (Höhe h=ℓ/2) und
Balken sind in B fest verbunden (biegesteife Ecke). Der Balken ist im Bereich AB (auf der
Länge ℓ) durch eine konstante Streckenlast q0
belastet.
a) Bestimmen Sie die Auflagerreaktionen in D und die Seilkraft S.
b) Ermitteln Sie die Schnittgrößen N, Q und M im horizontalen Balken und stellen Sie diese unter
Angabe der ausgezeichneten Werte grafisch dar.
Gegeben: q0, ℓ, h = 12 l .
3