Geometrie 2011

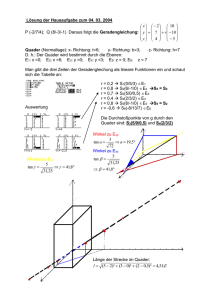
GEOMTERIE II.1
FRANZ LEMMERMEYER
II.1
Die Punkte O(0|0|0), A(4|3|0), B(0|3|6) und C(4|0|6) sind Eckpunkte eines
Quaders, dessen Kanten parallel zu den Koordinatenachsen sind.
Für jede reelle Zahl r ist eine Ebene Er : 6x1 + 8x2 + (r − 4)x3 = 6r gegeben.
a) Stellen Sie die Ebene E8 und den Quader in einem Koordinatensystem
dar.
Berechnen Sie den Winkel, den E8 mit der x1 x2 -Ebene bildet.
Zeigen Sie: Die Ebene E8 schneidet den Quader im Dreieck ABC.
Berechnen Sie den Flächeninhalt dieses Dreiecks.
b) Weisen Sie nach. dass die Gerade durch B und C in jeder Ebene Er
liegt.
Welche dieser Ebenen halbiert den Quader?
Bestimmen Sie r∗ so, dass die Ebene Er∗ orthogonal zu E8 ist.
Welche Schnittfigur entsteht beim Schnitt von Er∗ mit dem Quader?
1
2
FRANZ LEMMERMEYER
Lösungen
Wenn man nicht sieht, wie der Quader zu liegen hat, wird es schwer. Die andern
Ecken des Quaders sind jedenfalls P (4|0|0), Q(4|3|6), R(0|3|0) und S(0|0|6).
Zum Zeichnen von E8 : 6x1 + 8x2 + 4x3 = 48 bestimmt man die Spurpunkte
S1 (8|0|0), S2 (0|6|0) und S3 (0|0|12).
Zum Nachweis, dass ABC die Schnittfigur ist, genügt es offenbar zu zeigen,
dass A, B und C auf E8 liegen.
A
B
C
6 · 4 + 8 · 3 + 4 · 0 = 48
6 · 0 + 8 · 3 + 4 · 6 = 48
6 · 4 + 8 · 0 + 4 · 6 = 48
Da alle drei Gleichungen korrekt sind, liegt ABC in der Ebene.
Weil das Dreieck weder rechtwinklig noch gleichschenklig ist, muss man die
Höhe des Dreiecks mit Grundseite AB als den Abstand von C zur Geraden AB
bestimmen. Leichter geht es so: der Betrag des Kreuzprodukts zweier Vektoren
GEOMTERIE II.1
3
ist gleich dem Flächeninhalt des von diesen Vektoren aufgespannten Parallelogramms. Also gilt
−→
1 −→
F = |AB × AC|.
2
Wir finden
−4 0 −→
−→
18
AB × AC = 0 × −3 = 24 ,
6
6
12
also
√
18 2 = 6 · 4 = 6 29.
24
12
3
√
Also ist der Flächeninhalt des Dreiecks gleich 3 29 ≈ 16,2.
b) Die Gerade BC liegt in jeder Ebene, wenn die Punkte B und C in jeder
Ebene liegen:
B
6 · 0 + 8 · 3 + (r − 4) · 6 = 6r
C
6 · 4 + 8 · 0 + (r − 4) · 6 = 6r
Beide Gleichungen sind korrekt.
Damit ist jede Ebene Er eine Ebene, die man durch Drehung um die gemeinsame Achse BC aus E8 erhält. Der Quader wird offenbar halbiert, wenn Er
senkrecht verläuft, wenn also Er parallel zur x3 -Achse verläuft, oder wenn Er
durch P geht.
Einsetzen von P (4|0|0) in Er liefert r = 4: in diesem Fall ist E4 : 6x1 +8x2 = 24
in der Tat parallel zur x3 -Achse.
4
FRANZ LEMMERMEYER
6 6
Die Normalenvektoren von E8 und Er∗ sind ~n = 8 und ~n∗ = ∗8 . Damit
r −4
4
diese orthogonal sind, muss 6 · 6 + 8 · 8 + 4(r∗ − 4) = 0 sein, also r∗ = −21.
Die Spurpunkte von E−21 : 6x1 + 8x2 − 25x3 = −126 sind
S1 (−21|0|0),
S2 (0| − 15,75|0)
und S3 (0|0|5,04).
Von diesen Punkten liegt nur S3 im Quader, die Schnittfigur ist also das Dreieck
BCS3 .