dspace cover page - ETH E

Research Collection
Doctoral Thesis
Zur Faltbarkeit von Fachwerken
Author(s):
Calatrava, Santiago
Publication Date:
1981
Permanent Link:
https://doi.org/10.3929/ethz-a-000240711
Rights / License:
In Copyright - Non-Commercial Use Permitted
This page was generated automatically upon download from the ETH Zurich Research Collection. For more
information please consult the Terms of use.
ETH Library
Diss. ETH Nr. 6870
Zur Faltbarkeit
Fachwerken
von
ABHANDLUNG
Erlangung des Titels
zur
eines
DOKTORS DER TECHNISCHEN WISSENSCHAFTEN
der
EIDGENOESSISCHEN TECHNISCHEN HOCHSCHULE ZUERICH
vorgelegt
geboren
von
Santiago Calatrava Valls
28. Juli 1951
am
Spanien
von
Angenommen auf Antrag
von:
Kramel, Referent
Dipl. Ing. Robert Käser, Korreferent
Prof. Herbert
1981
Zur Faltbarkeit
von
Fachwerken
von
Santiago Calatrava Valls
Hl
b
am
IH
liAt. «"•
MATURA MATER ET MAGISTRA
I
Einführung
VERDANKUNGEN
Leitung meiner Doktorarbeit sowie die
vollen Anregungen möchte ich
Für die
Unterstützung mit
wert¬
Herrn Professor Herbert E. Kramel
recht herzlich danken.
Ebenfalls sehr dankbar bin ich
Herrn
Institut für
Korreferates.
vom
Dipl. Ing. Robert
Flugzeugstatik
Kaeser
und Leichtbau für die Uebernahme des
Brauchli,
Ein besonderer Dank gebührt ebenfalls den Herren Professoren H.
H. Hauri und H. Hugi für die Lesung meines Manuskriptes.
Im weiteren möchte ich den
Mithilfe danken:
folgenden
S. Burki
S. Lucek
B. Rothenberger
U. Niederhauser
D. Consolascio
Personen recht herzlich für ihre
Manuskript
in
sprachlicher
Fotos der Modelle
„
^
.,
„.-,-,-,
Hinsicht
Inhaltsverzeichnis
Seite
I
EINLEITUNG
Zielsetzung
Uebersicht
II
THEORETISCHE GRUNDLAGEN
Ebene und räumliche Fachwerke
Elemente zur Faltung von Fachwerken
Modu.lares Bauprinzip
III
II-l
II-6
11-19
PRINZIPIEN DER FALTBARKEIT MIT RHOMBEN ALS GRUNDELEMENTEN
Der Rhombus als Grundelement der Faltbarkeit.
Allgemeine Eigenschaften
des Rhombus
Rhombische Grundelemente für die Faltbarkeit in der
Ebene
Uebertragung des Prinzips der Faltbarkeit des Rhombus
111-19
Rhomboidale Grundelemente für die Faltbarkeit im Raum
111-28
viereckiger Projektion auf die Ebene TT
sechseckiger Projektion auf die Ebene TT
dreieckiger Projektion auf die Ebene TT
111-28
111-46
111-50
.
.
Element mit
Element mit
Element mit
PRINZIPIEN DER FALTBARKEIT MIT POLYEDERN ALS GRUNDELEMENT
Das vierfach
abgestumpfte
Oktaeder als Grundelement der
Faltbarkeit im Raum
IV-2
Der Kubus als Grundelement der Faltbarkeit
IV-17
Anwendung des Prinzips der Faltbarkeit des Kubus
IV-27
Geometrische
Gebilde
Bedingungen der Faltbarkeit ebener sechseckiger
Uebertragung des Prinzips der Faltbarkeit des Kubus auf
andere Strukturen
V
III-6
auf rhomboidale Formen
.
IV
III-l
IV-39
IV-46
DIE FALTUNG SPHAERISCHER FACHWERKE
V-l
Einführung
Die
Zur
Montagekuppel als Beispiel sphärischer Fachwerke
Geometrie sphärischer Fachwerke
Prinzipien der Faltbarkeit sphärischer Fachwerke
.
Die Faltbarkeit
pyramidaler
Elemente
v-3
V-6
V-18
Seite
Anwendung der vorher definierten Prinzipien
Faltung räumlicher Strukturen
.
.
.
.
.
triangulierte abgestumpfte Oktaeder
triangulierter Kubus
doppelt triangulierter Kubus
doppelt trianguliertes Pentagondodekaeder
doppelt trianguliertes abgestumpftes Ikosaeder
einfach
einfach
Weitere
VI
zur
Teilungsarten
der
Sphäre
WEITERE LOESUNGEN ZUM PROBLEM DER FALTUNG VON RAUMFACHWERKEN
ZUSAMMENFASSUNG
LITERATURVERZEICHNIS
V-30
V-32
V-42
V-53
V-66
V-83
V-90
VI-1
ZIELSETZUNG
Gegenstand dieser Arbeit ist die Geometrie des Aufbaus faltbarer fachwerkartiger Tragstrukturen.
Ziel der Arbeit ist
geometrischer Zusammenhänge, die
systematische Untersuchung dieser Zusammenhänge und deren Uebertragung
auf Gebilde aus Stäben und Knoten (Fachwerke), um faltbare Strukturen
zu erhalten. Das Schwergewicht liegt dabei auf der Untersuchung "Modularer
das Formulieren
Grundelemente" für die
Bildung faltbarer Strukturen.
Das Anordnen dieser Elemente in ebenen oder räumlichen Netzen lässt Fach¬
entstehen, die über ihre primäre Funktion als Tragstrukturen hinaus
ausgebildet sind, dass sie gefaltet werden können.
werke
so
UEBERSICHT
Einführung
Zuerst wird eine kurze
Themas "Fachwerke"
zu
den verschiedenen
Begriffen
des
ebene und räumliche Fachwerke, Stabilität.
gegeben:
Anschliessend wird auf das Thema "Faltbarkeit"
eingegangen,
Begriff
der
definiert, Fachwerke als faltbare Mechanismen betrachtet, deren Teile, ins¬
allgemein
besondere Gelenke, beschrieben sowie ganz
der
Ermittlung
von
Freiheitsgraden
zahl Stäbe und Knoten
bildung
von
eingegangen.
von
auf die Frage nach
Mechanismen als Funktion der An¬
Im weiteren wird das Problem der Aus¬
Begriff
Fachwerken behandelt und der
definiert.
Danach
beginnt das eigentliche Kapitel betreffend die Ausbildung faltbarer
gegliedert:
Fachwerke. Es ist in drei Teile
Prinzipien der Faltbarkeit
von
Der erste Teile behandelt
Rhomben als Grundelemente. Im zweiten Teil
Fachwerken, die in einer Ebene
gefaltet werden können sowie bezüglich räumlicher Fachwerke, die sich
wird der Frage
parallel
zu
bezüglich
der
Ausbildung
von
einer Ebene falten oder entfalten lassen,
nachgegangen.
Beispiele gebracht, die die mögliche Anordnung des 'Modularen
Grundelementes' zur Bildung ebener oder räumlicher Fachwerke erläutern.
Diese Beispiele werden beschrieben und- anhand von Modellen illustriert.
Dazu werden
Prinzipien der Faltbarkeit mit Polyedern als Grundelemente
aufgezeigt. Es wird von Polyedern ausgegangen, die durch geometrische Trans¬
Analog
werden
formationen und durch das Ersetzen der Kanten durch Stäbe und das Ersetzen
der Ecken durch Knoten, die die Stäbe
Grundelementen
gemacht
gelenkig verbinden,
zu
faltbaren
Dies wird hier anhand
werden.
von
zwei
Polyedern untersucht. Entsprechend
werden
erzeugt, die sich unmittelbar durch das Aneinanderreihen modularer
Elemente ergeben oder durch die Uebertragung und Abwandlung der Eigenschaften
der so definierten Elemente an andere endliche Gebilde, wodurch neue zusammen¬
Strukturen
faltbare Grundelemente
generiert werden,
den auch hier die untersuchten Fälle mit
Der
vorangehenden Abschnitt
Beispielen illustriert.
wie im
sphärischer
anschliessende Abschnitt behandelt das Problem der Faltung
Fachwerke. Es wird vorerst ganz
allgemein
an
wer¬
die Frage nach der
Faltung
Fachwerkgebilden, die sich nicht zu einer planparallelen, sondern zu
einer räumlichen Fläche bilden, herangegangen. Hier wird anhand sphärischer
von
Fachwerke ein
Weg gewiesen, der nachträglich
zu
weiteren Gebilden führen
kann.
Es werden
Fragen bezüglich der Erzeugung 'Modularer Grundelemente' und
Faltung räumlicher Flächentragwerke, die hier am konkreten
Bildung sphärischer Fachwerke angewandt werden, behandelt.
Problem der
der
Beispielserie die Komplexität
definierten Prinzipien belegt.
Anschliessend werden anhand einer
zeugten Gebilde und die vorher
der
er¬
II Theoretische Grundlagen
II-l
II Theoretische Grundlagen
DAS FACHWERK
Ziegler definiert diesen Begriff in seinem Buch "Mechanik, Band I,
Statik der starren und flüssigen Körper sowie Festigkeitslehre" (Birk¬
häuser Verlag Basel und Stuttgart, 1960, S. 41) wie folgt:
H.
"Unter einem idealen Faohwevk versteht man ein System von
Stäben, das folgenden Bedingungen genügt: Die Stäbe sind
reibungsfrei gelenkig miteinander verbunden und im Ver¬
gleich zu den Lasten so leicht, dass sie als gewichtslos
gelten können; die äusseren Kräfte (Lasten und Reaktionen)
greifen nur in den Knoten an. Diese Voraussetzungen ideali¬
sieren das wirkliche Fachwerk (bei dem insbesondere die
Verbindung der Stäbe vielfach durch Vernieten oder Verschweissen erfolgt); die mit ihnen erhaltenen Resultate
lassen sich aber nötigenfalls leicht verfeinern."
Ein Fachwerk besteht demnach
geraden Stäben, die in den Knotenpunkten
aus
gelenkig miteinander verbunden sind.
-
Sind alle Stäbe
parallel
einer Ebene,
zu
so
handelt
es
sich
um
ein
ebenes Fachwerk.
-
Sind die Stäbe nicht
parallel
zu
einer Ebene,
so
handelt
es
sich
um
ein
räumliches Fachwerk.
Die Stäbe und die Knoten sind die Bestandteile des Fachwerks. Ihre gegen¬
seitige Anordnung sowie ihre Ausbildung sind bestimmend für die statischen
und konstruktiven
Vom statischen
Eigenschaften des Fachwerks.
Gesichtspunkt
aus
sind die
Tragfähigkeit
und die Formstabilität
wichtigsten Eigenschaften eines Fachwerks. Die Tragfähigkeit erfordert
die
zweckmässige Ausbildung aller Bauteile entsprechend ihrer Beanspruchung,
währenddem die Formstabilftät die Erhaltung der Form im ganzen Tragsystem
eine
verlangt.
Aus dem Buch "Baustatik I"
und
F.
Stüssi, S. 118, Birkhäuser Verlag Basel
man
folgende allgemeine Formel, mit der das
von
Stuttgart, 1962, entnimmt
zahlenmässige Verhältnis zwischen
Stäben und Knoten ermittelt werden
bei welchem ein ebenes Fachwerk noch formstabil ist:
kann,
Il-la
2g
wobei: g
n
=
n
3,
=
Anzahl Knoten
=
Anzahl Stäbe.
Wird diese
Gleichung erfüllt,
richtig angeordnet,
Die
+
Bedingung 2g
=
so
n
+
und sind die Stäbe
als weitere
-
Bedingung
-.
ist das Fachwerk formstabil.
3 ist
Formstabilität des Fachwerks
zwar
zu
notwendig, aber nicht hinreichend,
sichern.
um
die
II-2
Untersuchen wir ein einfaches ebenes Fachwerk
bezüglich
seiner
Stabilität,
ergibt sich folgendes:
so
Variante A:
O
O
g
n
=
8
=
13
2g
3
n +
=
2-8 =13+3
Das Fachwerk ist formstabil.
Variante B:
9
6
g
=
n
=
2g
2 8
8
13
n
=
=
+
3
13
+
3
In diesem Fall ist das Fachwerk
Die Stäbe
instabil, obwohl die Gleichung erfüllt ist.
jedoch sind nicht richtig angeordnet.
II-3
Variante C:
Wenn
2g
< n +
3,
so
hat das Fachwerk
überzählige
Stäbe
(u),
O
O
wobei:
u
=
n
u
=
14
2g
-
16
-
3
+
+
3
überzähligen Stäbe
Die
u
ist
jene Anzahl Stäbe, die
vom
Fachwerk entfernt
werden können, ohne dass die Formstabilität des Fachwerks dadurch beein¬
trächtigt wird.
•¦
,
.
Variante D:
2g
Wenn
>
n
+
3,
so
ist das Fachwerk instabil. In diesem Fall
(F)
"fehlenden Stäben"
sprechen
wir
von
,
O
o
0
o
o
wobei:
F
n
g
F
=
2g
=
12
=
8
=
16
-
n
12
-
3
=
1
Mit "fehlende..Stäbe
tigen. Ort
F" bezeichnet
in die Struktur
man
die minimale Anzahl Stäbe, die
eingeführt werden
am
rich¬
muss, damit diese stabil wird.
II-4
folgende
Im Fall des räumlichen Fachwerkes kann die
Formstabilität des Fachwerks
häuser
=
Anzahl Stäbe
g
=
Anzahl Gelenke.
3g
S.
159, Birk¬
Gleichung erfüllt, und sind als weitere Bedingung die Stäbe richtig
ist das Fachwerk formstabil.
so
6,
< n +
u
3g
I",
6,
=
angeordnet,
Ist
n +
n
Wird diese
Wenn
F. Stüssi "Baustatik
Verlag Basel und Stuttgart, 1962):
3g
wobei:
geben (aus
Formel Auskunft über die
=
6,
> n +
F
Beispiel
=
hat das Gebilde
so
n
so
3g
3g
-
+
überzählige Stäbe (u):
6.
ist die Anzahl "fehlender Stäbe
-
n
-
F"
6.
anhand eines elementaren räumlichen Fachwerks:
ein Oktaeder, dessen Kanten durch Stäbe ersetzt werden, die in
den Ecken gelenkig miteinander verbunden sind, so entsteht folgendes Fachwerk:
Denken wir
uns
a)
n
g
3g
3g
=
12
=
6
=
n +
6
=
n +
6
3-6 =12+6
Das Fachwerk ist formstabil.
II-5
b)
n
13
=
g
6
=
3g
< n +
6
13
+
3-6
<
6
überzählige Stäbe
Anzahl
3g
6
+
u
=
u
=13 -36 +6=1
n
-
u:
c)
n
g
3g
3-6
=
11
=
6
>
n +
6
11
+
>
6
Das Gebilde ist instabil.
Anzahl "fehlende Stäbe
F
=
3g
F
=
3-6
n
-
-
-
11
6
-
6
=
1
F":
II-6
ELEMENTE ZUR FALTUNG VON FACHWERKEN
Die
Faltung als Formveränderung eines Fachwerks steht im Widerspruch
zur
Das heisst: damit ein Fachwerk
Stabilität als formerhaltende
Eigenschaft.
gefaltet werden kann,
instabil werden. Dies kann erreicht werden, in¬
dem
Bindungen
faltbar,
wenn
muss es
gelöst werden. Demnach
der Stäbe in den Knoten
durch
gezielte Lösung
Stabbindungen in den
der
ist ein Fachwerk
Knoten gegen¬
seitige Bewegungen zwischen den Stäben möglich sind.
Bei der ebenen Faltbarkeit bleiben die Stäbe eines Fachwerks während des
Faltvorgangs parallel
ganzen
einer Referenzebene. Bilden sie während des
zu
Faltvorgangs hingegen ein räumliches Gebilde,
so
sprechen
wir
von
der räum¬
lichen Faltbarkeit.
Folglich impliziert der Faltvorgang eine gegenseitige Bewegung der Teile,
d.h. die Drehung um eine beliebige Achse bzw. die Verschiebung in eine be¬
oder eine Kombination
liebige Richtung
Aus der
von
beidem.
Forderung, dass die Teile sich gegenseitig bewegen sollen, folgt,
dass faltbare. Fachwerke nicht
nach statischen «nd konstruktiven, sondern
Gesichtspunkten ausgebildet
auch ,nach kinematischen
derart beschaffen
nur
sein müssen. Sie sollen
sein, dass gegenseitige Drehungen und Verschiebungen mög¬
lich sind.
Tragfähigkeit
Nebst der Stabilität und der
sätzliche kinematische
Aspekte
zu
sind für faltbare Fachwerke
zu¬
berücksichtigen.
und
Faltung einen Mechanismus, der aus Stäben
Gelenken besteht, und der sich am Schluss des Faltvorganges durch Arretie¬
ren
der
Das Fachwerk bildet während der
gelösten Verbindungen
in ein stabiles Gebilde umwandeln lässt.
Betrachten wir ein Fachwerk als Mechanismus,
so
stossen wir in ein sehr
breites Gebiet der Technik vor,.und wir können letztlich diesen Mechanismus
als "Maschine" betrachten.
Dazu übernehmen wir die Definition
von
Rouleaux, die im Buch
"Angewandte Getriebelehre" (VDI-Verlag Düsseldorf, 1961)
von
Kurt Heim
zitiert wird:
II-7
"Eine Maschine ist eine Verbindung widerstandsfähiger
Körper, die so eingerichtet sind, dass sie mittels ihrer
(mechanischen) Naturkräfte gezwungen werden können, unter
bestimmten Bewegungen bestimmte Wirkungen auszuüben.','
Und weiter:
"Eine Maschine besteht aus einzelnen Mechanismen, die mitei¬
nander in abgestimmtem Wechselspiel die verlangten Wirkungen
hervorrufen. Solche Mechanismen werden Getriebe genannt. Es
ist nun durchaus möglich, dass bereits ein einzelnen Getriebe
eine Maschine darstellt, wie z.B. eine Schraubenpresse. Meist
aber sind es mehrere Getriebe, die das Gebilde Maschine er¬
geben ."
Wir übernehmen die Definition
von
J. Volmer
(VEB-Verlag Technik, Berlin, 1976,
S.
aus
dem Buch "Getriebetechnik"
17):
"Ein Getriebe ist eine mechanische Einrichtung zum Uebertragen
von Bewegungen und Kräften oder zum Führen von Punkten eines
Körpers auf bestimmten Bahnen. Es besteht aus beweglich mitei¬
nander verbundenen Teilen (Gliedern), wobei deren gegenseitige
Bewegungsmöglichkeiten durch die Art der Verbindungen (Gelenke)
bestimmt sind. Ein Glied ist stets Bezugskörper (Gestell), die
Mindestzahl der Glieder und Gelenke beträgt jeweils 3."
So betrachtet sind die faltbaren Fachwerke
Getriebe, deren Glieder Stäbe sind,
die mit Gelenken miteinander verbunden werden. Deren Studium ist
Gegenstand
gleichzeitig
der Getriebetechnik,
stand der Statik. Als
Tragwerk
jedem seiner einzelnen Teile.
muss
Das
sind
jedoch die Fachwerke Gegen¬
ein Fachwerk formstabil sein.
heisst, dass das Fachwerk, das während des
Faltzustandes ein labiler Mechanismus ist, im entfalteten Zustand formstabil
sein soll. Beide Zustände unterscheiden sich demnach in der Anzahl Freiheits¬
grade des Gebildes.
Während des
Faltvorgangs ist der Freiheitsgrad
stand ist F
_<
Unter dem
Anzahl
ser
F > 0 und im entfalteten Zu¬
0.
Freiheitsgrad eines Körpers in einem Bezugssystem versteht
man
die
unabhängige Einzelbewegungen (Drehungen und Verschiebungen), die die¬
Körper ausführen kann.
II-8
Freiheitsgrad eines Mechanismus F stimmt überein mit der Anzahl unab¬
hängiger Bewegungen, die die verschiedenen Teile des Mechanismus ausführen
Der
können.
Fachwerke, d.h. die gegenseitige Bewegung zwischen den
Teilen, wird durch die Bewegung in den Gelenkelementen ermöglicht.
Die Faltbarkeit der
einzelnen
folgenden werden verschiedene Gelenksarten studiert. Es werden deren Be¬
wegungsarten, die Gelenkfreiheitsgrade sowie deren Verhältnis zum Gesamtfreiheitsgrad des Mechanismus untersucht.
Im
Als Grundform der
die
Relativbewegung der Teile im Gelenk haben wie die Drehung,
Verschiebung sowie deren Kombination.
II-9
Gelenkarten bei Mechanismen
Drehgelenk:
Dieses erlaubt die Drehung um eine Achse. Gelenkfreiheitsgrad f
(f Anzahl Freiheitsgrade beim betrachteten Gelenk)
=
1
=
7/
MSI
TU!
<\
n:
Va
m
Schiebegelenk:
Dieses erlaubt die
Verschiebung in eine Richtung. Gelenkfreiheitsgrad f
/y
<
Die oben schematisch
>
1
?zm™
i
<
>
dargestellten zwei Gelenksarten erlauben die zwei
Grundbewegungen Drehung und Verschiebung.
Durch Kombination dieser zwei
lenke
zu
Grundbewegungen ist
es
möglich,
bauen, die höhere Bewegungsfreiheiten erlauben.
weitere Ge¬
=
1
11-10
Zum
-
Beispiel:
Drehschiebegelenk:
Gelenkfreiheitsgrad
f
=
2
>
<
•?
^
-y
-^
Dreifaches
C
Drehgelenk, auch Kugelgelenk genannt:
Gelenkfreiheitsgrad
f
=
3
A*
T7
/>
i>
V
\y
V
o
3
11-11
Weitere Gelenksarten
Gelenke mit höherer
spricht
Man
nachdem, ob
Gelenkwertigkeit:
einfacher, zweifacher, dreifacher etc. Gelenkwertigkeit, je
zwei, drei, vier usw. Stäbe am gleichen Gelenk gleichachsig mit¬
von
einander verbunden sind.
Sind in einem Punkt
verbunden,
insgesamt
handelt
so
es
sich
n
gleichachsig (koaxial) miteinander
einen Gelenkanschluss mit (n-l)-facher
Stäbe
um
Wertigkeit. Dieses mehrfache Drehgelenk ist kinematisch gleichwertig mit n-l
einfachen Drehgelenken (mit zwei anschliessenden Stäben).
Va
K
«^
'A
rc
unabhängige Stäbe mit einer gemeinsamen Drehachse.
Es ist ein Gelenkanschluss mit doppelter Wertigkeit. Es ist demnach kine¬
matisch gleichwertig mit zwei Drehgelenken mit dem Gelenkfreiheitsgrad
zeigt
Das Schema
f
1 und einfacher
=
Fasst
keit
f
man
Es
in einem Mechanismus die Gelenke mit f
man
g,,, als
1 und einfacher
=
Wertigkeit.
gleich wie die Gelenke mit f
erhält
so
drei
=
äquivalente
1 und einfacher
1 und höherer
=
Wertigkeit
Gesamtzahl Gelenke mit
Wertig¬
zusammen,
Freiheitsgrad
Wertigkeit.
gibt folgenden Zusammenhang:
m
g(l)
wobei: g.
=
=
gi
2g2
+
+
3g3
Anzahl Gelenke mit f
+
=
%
2
+
i=l
i*gi
/
1 und i-facher Wertigkeit,
d.h. mit i+1 koaxial verbundene Stäbe.
Ist
n
die Anzahl der
am
selben Knoten der Struktur zusammenstossenden koaxial
miteinander verbundenen Stäbe, dann ist i
=
n-l.
11-12
Frage wie die Gelenke ausgebildet werden müssen,
Im weiteren stellt sich die
damit diese beiden
1. Die
Anforderungen erfüllt werden können:
notwendigen Bewegungen während des Faltvorganges sollen
ermöglicht werden.
2. Die Gelenke sollen im Stande sein, die
den
an
Knotenpunkten wirkenden
Kräfte aufzunehmen.
Im
Zusammenhang
Freiheitsgrad bzw.
mit dem
wird in dieser Arbeit
speziell
Wir unterscheiden zwei Arten
der Formstabilität des Fachwerks
Anforderung eingegangen.
auf die erste
Mechanismen: ebene und räumliche Mechanismen.
von
Ebene Mechanismen sind solche, bei denen sich alle Punkte des Gebildes in
ebenen Bahnen
um
bewegen. Sind diese Bahnen räumliche Kurven,
so
handelt
es
sich
räumliche Mechanismen.
Grundformel
Ermittlung der Anzahl Freiheitsgrade F des
zur
F
3 (n-l)
=
2g(1)
-
ebenen Mechanismus
g(2)
-
(aus: J. Volmer: "Getriebetechnik", S. 46,
VEB-Verlag Technik, Berlin, 1976)
wobei:
n
g
g
=
=
{
'
=
Anzahl Stäbe
äquivalente Gesamtzahl Gelenke mit
äquivalente
f
=
Gesamtzahl Gelenke mit f
=
F
=
3
¦
Mit I kann die Formel II wie
(n-l)
-
2
1 und einfacher
(siehe S.
2
folgt ausgedrückt werden:
(g;L
+
2g2
+
3g3
+
4g4 +
..
.)
-
g(2)
Wertigkeit
11-11)
11-13
Beispiel:
Siebengliedriger Mechanismus:
f=
f=
o
M
f=2
o
=
F
wobei: g,,.
(2)
Infolge
3 (n-l)
=
2g(i) g(2)
-
-
=
Anzahl Gelenke mit f
=
1
=
Anzahl Gelenke mit f
=
2
der verschiedenen
g(l)
=
gi
+
Wertigkeit der Gelenke mit
2g2
3+2-2=7
(1)
=1
g(2)
F
=
3 (7-1)
F
=
3
Der Mechanismus hat
-
f=
2-7
-
1
folglich drei Freiheitsgrade.
f
=
1 erhalten wir:
11-14
Beispiel
2:
Betrachten wir
heitsgrade
nun
das Fachwerk
Seite II-2 und berechnen dafür die Frei¬
von
der dort nach FöRnstabilität untersuchten Varianten.
Variante a):
O
©
o
2g (1)
3 (n-l)
\
n
12
=
g
g
=
g
=
3 Gelenke mit f
=
3
=
+
2g
=
1 und einfacher
+
3g
+
4g
(Anzahl Gelenke mit f
"
"
"
zweifacher
1
"
"
"
"
dreifacher
g„= 1
"
"
"
"
vierfacher
g
1)
Wertigkeit
"
g
=
g=3+2-3+3-l+4-l=16
F
=
3 (12-1)
-
2-16
=
1
Der Mechanismus hat somit einen
Vergleicht
man
Freiheitsgrad.
dieses Resultat mit
demjenigen
von
Seite
II-2,
so
.stellen wir
fest, dass die Anzahl Freiheitsgrade mit der Anzahl fehlender Stäbe F über¬
einstimmt.
11-15
So kann
in diesem Fall den
man
Stäbe definieren, die
Freiheitsgrad
die Struktur
an
des Fachwerks als die Anzahl
angeschlossen werden müssen, damit
sie formstabil wird.
Variante b):
o
o
F
=
3 (n-l)
n
=
13
g(l)
=
g
=
+
des Fachwerkes
=
2g (1)
2g2
2-4
zwischen dem
Vergleich
F
2
+
=3 (13-1)
F
Der
gi
-
+
3g3 4g4
+
3-0
+
-
+
2-18
4-2
=
=
18
0
Freiheitsgrad
und der Anzahl der
notwendigen Stäbe ergibt wiederum:
F
zur
Stabilisierung
11-16
Variante c)
n>
o
0
F
=
n
=
3 (n-l)
14
g(l) =gi
g
+
2g2 3g3 4g4
+
(14-1)
=3
2g
F
=
n
=
14
=
8
=
2-8
F
Das Fachwerk hat
=
F
-
=
erhält
20
-1
der Anzahl der
man:
3
-
14
-
folglich
Wie bei den beiden
F
n
-
2*20
bezüglich
F,
Fachwerks fehlenden Stäbe
9
-
das Fachwerk
man
+
1 + 2-4 + 3-1 + 4-2
=
F
Untersucht
2g 1)
-
3
=
einen
-
1
überzähligen
Stab.
vorangehenden Fällen ergibt sich:
zur
Stabilisierung des
11-17
Daher können wir sagen:
a)
Ist ein Fachwerk
Fachwerks mit
formstabil,
derjenigen
zur
so
stimmt die Anzahl
Freiheitsgrade
des
Stabilisierung des Fachwerks notwendigen
Anzahl Stäbe überein.
b)
Ist ein Fachwerk formstabil und weist
d.h. ist die Anzahl fehlender Stäbe
grade
F
=
F
es
=
keinen
0,
so
überzähligen Stab auf,
ist die Anzahl Freiheits¬
0.
überzählige Stäbe auf, d.h.
F -u, so stimmt die Anzahl überzähliger Bindungen des Mechanismus mit
-u.
der Anzahl überzähliger Stäbe überein, d.h. F
c) Ist ein Fachwerk formstabil und weist
es
u
=
=
Freiheitsgrade gleich der Anzahl der
Stabilisierung des Fachwerks notwendigen Stäbe.
In allen drei Fällen ist die Anzahl
zur
Beim räumlichen Fachwerk wird die Anzahl der fehlenden Stäbe
de Formel
gegeben:
F
wobei: g
=
n
=
Analog
zum
=
3g
n
-
g
=
=
3g
F
=
3*6
n
-
-
Seite
II-4)
,
Fall des ebenen Fachwerkes können wir sagen, dass F
6
=
(vgl.
Anzahl Stäbe.
11
F
6
-
Anzahl Gelenke
Beispiel:
n
F durch folgen¬
-
11
6
_
6
=
1
=
F.
11-18
Dieses
Beispiel
wurde auf Seite II-5 behandelt. Dort
den Stäben". Hier
die
Freiheitsgrade
ren, die
wird.
an
sprechen wir
von
sprachen
"Freiheitsgraden". Folglich
wir
von
könnte
"fehlen¬
man
einer räumlichen Struktur als die Anzahl Stäbe definie¬
die Struktur
angeschlossen
werden müssen, damit sie formstabil
:
11-19
MODULARES BAUPRINZIP
gesehen sollten Stäbe und Gelenke des Fachwerks im Hinblick
auf eine Standardisierung der Teile möglichst einheitlich sein. Das Aneinan¬
derreihen von Grundelementen (Stäbe und Gelenke) zu Fachwerken basiert auf
Konstruktiv
den "Modularen
Bauprinzipien".
Demnach werden die Bauteile in einem Raster
.
.
angeordnet.
Der Raster ist ein
geometrisches Ordnungsprinzip, das die Lage der verschie¬
denen Teile des Gebildes in der Ebene oder im Raum bestimmt. Damit ein Raster-
gebildet werden kann, muss die Summe der Winkel zwischen den
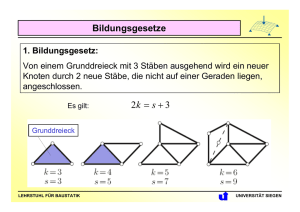
benachbarten Stäben, die am gleichen Knoten zusammenstossen, gleich 360° sein.
ih der Ebene
Beispiele
baut sind:
Dreieck:
von
Rastern, die auf Quadraten, Sechsecken und Achtecken aufge¬
11-20
Sechseck:
Quadrat:
Rhombus:
11-21
Trapez:
Quadrat und Achteck:
11-22
Zur
Bildung
Netzen im Raum
von
betrachten wir hier vorerst diejenigen räum¬
lichen Gebilde, die durch parallele Ebenen begrenzt sind. Deren Projektion
auf eine Ebene
TT
bildet einen
quadratischen bzw« sechseckigen
Raster.
Beispiel:
/
/
/
^
;**
Als weitere
Beispiele räumlicher
Netze betrachten wir unter anderem
diejeni¬
regelmässigen oder halbregelmässigen Polyedern ergeben,
bzw. diejenigen, die sich durch die Triangulierung der Sphäre in weitere
polyedrische Formen ergeben. (Siehe S. V-13, V-14)
gen, die sich
aus
Beispiele räumlicher sphärischer
Netze:
1. Oktaeder;
Sphärisches
Dreiecke.
Netz
gleichseitiger
11-23
2.
Abgestumpftes Oktaeder;
Sphärisches
Netz
von
Quadraten
und Sechsecken.
3.
Abgestumpftes Oktaeder einfach trianguliertf
Sphärisches
Dreiecke.
Netz
gleichschenkliger
III
Prinzipien der Faltbarkeit
mit Rhomben als Grundelemente
III-l
III
Prinzipien der Faltbarkeit mit Rhomben als Grundelemente
DER RHOMBUS ALS GRUNDELEMENT DER FALTBARKEIT
Allgemeine Eigenschaften des Rhombus
Gegeben
sei ein Rhombus mit den Ecken A, B, C, D und der
Seitenlänge
a.
Die
gegenüberliegender Ecken seien variabel und in Abhängigkeit
a, der gebildet wird durch die zwei benachbarten Seiten AB
Abstände zweier
vom
Winkel A
und AD. Das
=
bedeutet, dass die Diagonalen
d1
und
d2
einerseits und die Win¬
kel B, C, D andererseits als Funktion des Parameters
können.
>>
180
d2
So
ergibt sich:
d
d2
A
A
fc
=
2
a cos
a/2
=
2
a
sin
a/2
=
a
A
=
C
A
_
D
_
TT
-
a
a
ausgedrückt werden
III-2
Entsprechend kann die Fläche des Rhombus als Funktion des
folgt ausgedrückt werden:
F
=
für
d
yd
a
=
2
=
tt/2
¦+
a2
F
cos
=
F
a/2*sin a/2
=
max
=
a2
Parameters a wie
sin a
a
/\
90
Für a
=
0
bzw.
a
=
TT
wird F
=
180°
>a
0, d.h. alle Seiten des Rhombus liegen
auf
einer Linie.
4^
a=0° a=30"
a=t5°
a=90°
a=135°
a=150°
a=180°
III-3
Die
a
=
Enveloppe der verschiedenen Positionen der Seite AB des Rhombus von
0 bis a
TT, bezogen auf die Achsen eines rechtwinkligen Koordinaten¬
=
systems XY mit Ursprung im Zentrum des Rhombus A, B, C, D, kann durch die
Clairautsche
Differentialgleichung ermittelt werden:
y
Diese nimmt in
unserem
y'
=
C
xy'
+
=
¦
xy
g(y')
folgende
Fall die
y
Für
=
y
+
/y'2
F(x,y,c)
II)
F
an:
a
+
(Parameter), bezogen auf den
I)
Form
ersten
ex +
=
(x,y,c)
1
=
x
Quadranten, ergibt sich:
ca
/c2
1
+
-y
+
0
=
=
/(c2
+
1)3
I) nach C aufgelöst und in II) eingesetzt ergibt:
y
Dadurch ist die
Enveloppe
=
(a
,
2/3
x
-
im ersten
2/3,3/2
)
Quadranten
definiert:
/\
J
>x
0
III-4
Analog dazu werden die Enveloppen der Seiten BC,
CD und DA ermittelt.
/\
X<
>X
-a
v
III-5
Modulares
Man
Bauprinzip
beachte, dass für einen beliebigen Winkel
a
ein Aneinanderreihen der
möglich ist, und dass sich die
einzelnen Elemente gleicherweise verformen wie die aas ihnen gebildete
Elemente in ein rhombisches Rasternetz
Struktur.
""'""
—
~
a=90#
a=6l"
III-6
RHOMBISCHE GRUNDELEMENTE FUER DIE FALTBARKEIT IN DER EBENE
Die Seiten des Rhombus ABCD werden durch vier
Drehgelenke verbunden,
in den Ecken durch
Ebene
zur
liegen.
Es entsteht
so
gleich lange
Stäbe ersetzt und
dass alle Drehachsen senkrecht
folgendes kinematisches Schema für
das Gebilde:
A_f=1
f=
f=l
C f=1
Mit
folgendem Freiheitsgrad:
n
=4
gl
=4
F
=3
(n-l)
~
F
=3 (4-1)
-
Da F
Man
=
1
2
q±
2*4
=
ist, handelt
1
es
sich
um
einen
zwangsläufigen Mechanismus.
beachte, dass das Dreieck als ebene elementare Figur unverzerrbar ist,
unmöglich, seine Fläche unter Beibehaltung aller Seitenlängen
zu verändern. Im Gegensatz dazu ist es beim Rhombus möglich, die Fläche bei
gleicher Seitenlänge a zu verändern, indem man den Winkel a ändert.
d.h.
es
ist
Betrachten wir das oben beschriebene Gebilde, das mit einem
Diagonalstab
sehen ist: Wir unterteilen in diesem Fall den Rhombus ABCD in die beiden
Dreiecke ABC und ACD.
ver¬
III-7
=
=
n
gi
g2
=
5
=
2
=
2
=
Das
zugehörige kinematische Schema ergibt folgenden Freiheitsgrad:
F
=
3
F
=
(n-l)
-
3 (5-1)
-
(g±
2
2 (2
Es handelt sich
dung
dem C
in C soll
um
+
+
g2)
2*2)
=
0
ein in der Ebene unverzerrbares
erlauben, die Länge der Diagonale beliebig
entlang dem Diagonalstab verschoben
und für
werden kann.
U
I
71
fo
I
i
i.
i
i
M
System. Die Gelenkausbil¬
ii
1i
1}
y
\
jeden
zu
Wert
verändern, in¬
von a
arretiert
III-8
Dadurch
ergibt sich die Möglichkeit, die
verformbaren des Rhombus
starre Form des Dreiecks mit der
kombinieren.
zu
zugehörige kinematische Schema ist:
Das
f=1
f=1
f=
Das Gelenk C kann in ein Dreh- und ein
voneinander
unabhängig sind.
=
C
=
3
=
2
F
=
3
F
=
3 (6-1)
n
gl
g2
Schiebegelenk unterteilt werden, die
(n-l)
-
-
2
(g
2 (3
+
+
2 g )
2*2)
1
zwangsläufig (Zwangsläufigkeit
Das
System
ren
des Gelenkes C wird das
ist
=
bedeutet F
System formstabil.
=
1). Durch Arretie¬
III-9
Wie
aus
der Definition des Modularen
hervorgeht, ist
es
möglich,
Bauprinzips der
die einzelnen Elemente
dass die Knoten der Modularen Grundelemente in die
lären rhomboidalen Netzes
zu
liegen
so
rhombischen Formen
aneinander
Schnittpunkte
zu
reihen,
eines regu¬
kommen.
arretierbares
Schiebegelenk
folgenden betrachten wir die Gruppierung von einzelnen Elementen in
einer übergeordneten Struktur und untersuchen deren kinematisches Zusammen¬
Im
spiel.
111-10
Es werden dabei zwei Varianten untersucht:
VARIANTE I
je parallelen Stäben (AB, CE,
AF, BJ, usw.) besteht, die in den Kreuzungspunkten durch einfache Drehge¬
Es sei ein
Gebilde, das
aus
zwei Scharen
von
lenke miteinander verbunden sind.
Es stellt sich die
von
Verbindungen (d.h.
Drehgelenken) ist, die zwischen die beiden Stabscharen eingefügt werden
Frage, welches die minimale Anzahl
ebener, zwangsläufiger
muss, damit das Gebilde als
Freiheitsgrad F
ergibt sich aus
=
=
1
der
folgenden Formel:
3(n-l)
=
2 gn
-
ergibt sich:
1
=
3(n-l)
O
=
3
n
-
eine ganze Zahl ist,
2
-
2 g
-
3n
Damit g
(d.h. mit dem
1) Mechanismus wirkt. Der Freiheitsgrad des Mechanismus
F
Für F
von
g3
-
2
muss n
eine
gerade Zahl sein.
III-ll
Tabelle der Werte für
n
und g
n
4
6
8
10
12
14
16
18
gl
4
7
10
13
16
19
22
25
Beispiel 1
In diesem Fall ist
Zwei
n
=
8, also ergibt sich
mögliche Gelenkanordnungen:
ro
g
=10.
111-12
Beispiel 2
folgenden Gebilde wird die minimale Anzahl der Gelenke bestimmt und
plaziert, dass ein ebener, zwangsläufiger Mechanismus entsteht.
Im
n
12
g1
Bedingung gelte,
schlüssen
zu
Es ist
beachten, dass:
-
zu
16
<2
\
Als weitere
=
so
dass
jeder Stab mit mindestens zwei Gelenkan¬
versehen ist.
Der Abstand zwischen den
Drehgelenken, die auf einem Stab liegen und diesen
mit weiteren Stäben des Systems verbinden, konstant bleibt und gleich n*a
ist (wobei n eine ganze Zahl und a die Seitenlänge eines Modularen Grund¬
elementes ist)
.
-
Infolge der Zwangsläufigkeit des Mechanismus bleibt die Parallelität zwischen
den einzelnen Stäben der
Die beiden
gleichen
Bedingungen ergeben,
dass die
mit den Stäben der anderen Schar
unabhängig
Schar
vom
Winkel
a
erhalten.
Lage der Kreuzungspunkte eines Stabes
unabhängig vom Winkel a konstant bleibt. In
den Kreuzungspunkten gibt es nur gegenseitige Drehung aber keine Verschiebung.
Weitere Drehgelenke können eingeführt werden, ohne dass sich eine zusätzliche
Bindung im Sinne einer Abminderung des Freiheitsgrades des entstandenen
111-13
ergibt.
Mechanismus
jedem Kreuzungspunkt zwischen
Im Extremfall können in
den beiden Scharen Gelenke vorhanden sein, etwa
konstruktiven Gründen
um aus
Haftung zwischen den Stäben sowie eine Abminderung der Knick¬
Stäbe bei Druckbeanspruchung zu ermöglichen.
eine bessere
länge
der
1), genügt eine einzige Diagonale, um es
System zwangsläufig ist (F
in ein formstabiles System umzuwandeln. Wird das eine Ende der Diagonale mit
Da das
=
Schiebegelenk versehen, so kann das System wahlweise form¬
stabil oder beweglich gemacht werden. Damit wird die Faltung wie auch die
einem arretierbaren
Fixierung des Systems ermöglicht.
VARIANTE II
Im
Fall, dass jeder Kreuzungspunkt des rhombischen Netzes als Gelenk ausge¬
bildet wird, also alle
an
gelenkig miteinan¬
einen Knoten anstossenden Stäbe
Länge der Stäbe auf den Abstand zwischen zwei
Kreuzungspunkten beschränkt wird, lässt sich der Freiheitsgrad wie folgt
der verbunden sind, und die
festlegen:
F
wobei:
2(g;L +
2
g2
+
3
g3)
g
=
Anzahl Gelenke mit 2 anschliessenden Stäben
=
Anzahl Gelenke mit 3 anschliessenden Stäben
=
Anzahl Gelenke mit 4 anschliessenden Stäben
der Gebilde wie
Freiheitsgrade
F
wobei: n, g
0
,
g
ergibt
und g
zu
=
-
2(g
2g2
+
ändern sich die
+
3g3>
-
d
System
sich ein formstabiles
0
=
minimale Anzahl
fixieren.
so
Ausgangssystem bestimmt wurden.
im
F
wobei: d*
Diagonalstäben ein,
von
folgt:
3(n-l)
=
d
-
Anzahl Stäbe
wir eine bestimmte Anzahl d
=
-
=
g^
Für F
(n-l)
n
g
Fügen
3
=
->-
d*
=
3
(n-l)
Diagonalen,
die
-
2(g
+
2g2
nötig ist,
+
um
3g3)
das ganze
System
111-14
Beispiel 1
n
gl
g2
g3
d*
=
44
=
6
=
12
=
10
=
3(44--1)
-
2 (6
+
2*12
+
3*10)
=
9
Diagonalstäben wird das ganze System formstabil ausgesteift.
In beiden Richtungen des Netzes muss in jeder Reihe mindestens ein Diagonal¬
stab vorhanden sein. Wird das eine Ende jeder Diagonalen mit einem arretier¬
baren Schiebegelenk versehen, kann das System wahlweise formstabil oder be¬
weglich gemacht werden. Damit wird die Faltung und auch die Fixierung des
Systems ermöglicht.
D.h. mit 9
111-15
Beispiel 2
n
=
gl=
g2
g3
19
8
=
2
=
4
Mit dem
F
=
Freiheitsgrad
3(19-1)
-
2(8
+
2*2
+
Anzahl der erforderlichen
3*4)
=
6
Diagonalen
arretierbare Schiebegelenke.
=
6.
Entsprechend
erhält das System 6
111-16
Die
folgenden
Bilder
zeigen
die Struktur
am
Modell während der
Entfaltung:
Bild 1:
Gefaltete Struktur
a
=
0
Bild 2:
a
=
30
Bild 3:
a
=
60
111-17
Bild 4:
•a
%
r& *
lrii
m
i
m
t Ja
=
120
Bild 5:
Ueberlagerung
dreier
verschiedener Etappen
des
Entfaltungsvor¬
ganges
111-18
Bilder 6,
7,"
Bild 6:
Drei Ansichten des
Knotens während des
Faltvorganges
c
111-19
UEBERTRAGUNG DES PRINZIPS DER FALTBARKEIT DES RHOMBUS AUF RHOMBOIDALE FORMEN
Vier Stäbe werden
durch Gelenke verbunden, dass eine
so
viergliedrige,
ebene
Drehgelenkkette entsteht. Das Gebilde wird als faltbar bezeichnet, wenn es
möglich ist, alle vier Gelenke bzw. alle fünf Stäbe auf die gleiche Linie
zu
legen.
Nehmen wir an, dass die
1. Falten wir das Gebilde so, dass sich das Gelenk C
AC
von
ABCD faltbar ist.
viergliedrige Drehgelenkkette
entlang der Diagonalen
A entfernt:
i
A
\A
Bei
gefaltetem Zustand zeigt sich, dass:
AB +
'•Als
BC"
=
AD +
DC~
Bedingung der Faltbarkeit ergibt sich, dass die Summe der Längen der
beiden Stäbe, die je auf einer Seite der Diagonalen liegen, gleich ist.
111-20
2. Falten wir das Gebilde so, dass sich das Gelenk C
entlang der Diagonalen
AC dem Gelenk A annähert:
/\
<-'
Es
zeigt sich,
dass:
AB
-
BC
=
AD
DC
-
ergibt sich als Bedingung der Faltbarkeit, dass die Differenz der
Längen der zwei Stäbe, die je auf einer Seite der Diagonalen liegen,
Es
gleich
sein
muss.
Faltvorgänge
sollen, ergibt sich:
Falls beide
-
Die beiden
der
AC
einzigen Gebilde ausgeführt werden
einem
I)
Ä¥+BC"=ÄD + DC"
ii
ä¥-bc" äd"-dc"
=
I + II
->
AB
I
->
BC
Bedingungen
Diagonalen
von
-
II
=
AD
=
DC
der Faltbarkeit
symmetrisch sein
implizieren, dass das Gebilde bezüglich
muss.
111-21
Beispiel
Bildung
eines ebenen zusammenfaltbaren Fachwerkes durch Aneinanderreihen
von
rhomboidalen Elementen.
Gegeben sei eine viergliedrige Drehgelenkkette
ABCD
X
o
a/2
mit den
Stablängenverhältnissen
'
AB
ÄD
=
1
CD
AD
^—
CB
CD
Aus den beiden Verhältnissen
Der
CB_
AB
II)
gonalen
=
ergibt sich, dass das Gebilde entlang der Dia¬
AC faltbar ist.
Freiheitsgrad
des Gebildes ist F
=
1.
Diagonalstab ein¬
Diagonalstab entlang ver¬
Wie im Fall des rhombischen Grundelementes können wir einen
führen und das Gelenk C
schoben und für
so
beliebige
ausbilden, dass
Werte
von a
es
dem
arretiert werden kann:
111-22
0
Das Verhältnis
von a zu
a
=
$
ist
folgendes:
2
are
sin
sinß
•5-4 sing
Betrachten wir die Faltintervalle
a£[o,TT/3]
und
ߣ"[o,Tr/3]
/\
1/3
n/3
>ß
111-23
Wie
(a
aus
=
0°)
der
in
Abbildung ersichtlich wird, kann
das gleichseitige Dreieck ABC (a
sich die
=
Segment AB
60°) umwandeln und umgekehrt.
vom
zwangsläufig, kann aber durch Fixieren des Stabes
ein formstabiles Gebilde (F
0) umgewandelt werden.
Das Gebilde ist
Gelenk C in
Figur
AC im
=
Durch Aneinanderreihen rhomboidaler Elemente entsteht
folgendes Gebilde:
.111-24
Die
folgende Photosequenz zeigt
die
Entfaltung
der Struktur
am
Modell:
Bild 1:
Gefaltete Struktur
Bild 2:
Anfangsstadium der
Entfaltung
mw
Bild 3:
.Zwischenstufe
der
Entfaltung
111-25
Bild 4:
Weitgehend
entfaltete
Struktur
Bild 5:
Um ein formstabiles Ge¬
bilde zu erhalten, wer¬
den diejenigen Knoten
fixiert, in denen
zuvor
Verschiebung der
Stäbe eine Bindung ge¬
zur
löst wurde.
111-26
Es ist
zu
1. Die
Bindungen
und .60
beachten:
der
Diagonalstäbe können bei jedem
Wert
von a
zwischen 0
arretiert werden. So kann durch
Fixierung der Bindungen in C für
jeden Zustand der Entfaltung eine formstabile Struktur gebildet werden.
I vanab«
2. Jedes Element kann
unabhängig
von
den benachbarten Elementen
entfaltet werden.
Beispiel:
Errichten eines
\
\
Steges
im
Schiebeverfahren
gefaltet oder
111-27
3. Durch
geeignete Wahl der Stablängen können verschiedene Fachwerkformen
gebildet werden.
Beispiele:
-
Zweigelenkbogen
ri
**
-
dreigelenkiges
Fachwerk
<\
111-28
Rhomboidale Grundelemente für die Faltbarkeit im Raum
MODULARES GRUNDELEMENT MIT VIERECKIGER PROJEKTION AUF DIE REFERENZEBENE
Betrachten wir zwei
deckungsgleiche Rhomben mit der Seitenlänge
TT
a,
mit den Ecken A, B, F, D bzw. A, C, F, E und der
Wird
nun
einer der Rhomben
eine räumliche
90
o
um
die
gemeinsamen Diagonale AF.
Diagonale AF gedreht, so entsteht
um
Figur mit den Ecken A, B, C, D, E,
F.
s\
90°
;*»¦
Bei konstanter
beiden
a wie
Seitenlänge
a
können die Abstände BD, CE und AF zwischen den
jeweils gegenüberliegenden
folgt ausgedrückt
Ecken verändert und als Funktion des Winkels
werden:
I)
II)
III) BC
BD
=
CD
=
DE
=
=
AF
=
2
a
cosa/2
CE
=
2
a
sina/2
=
t/2
Eß"
a
sina/2
111-29
Nehmen wir eine Referenzebene
zur
E
So
Ebene
in F an,
dass die
so
Diagonale
AF senkrecht
steht; zudem seien B', C', D', E' Projektionen der Punkte B, C, D,
TT
auf der Ebene
ergibt
TT
TT.
sich:
IV)
BB'
=
CC
DD'
=
=
EE'
=
a
cosa/2
liegen alle in einer Ebene parallel zu TT und bilden die
V2 a sina/2. Von dieser para¬
Quadrates mit der Seitenlänge a'
Die Punkte B, C, D, E
Ecken eines
metrischen
a
=
Abhängigkeit
der Seite a'
0, a' =0 ist und entsprechend
lichen
lässt sich ableiten, dass für
AF
von a
=
2
a
wird. Alle
Figur kommen auf eine Linie senkrecht
Modulares
Das
=
zur
Segmente der ursprüng¬
Ebene TT zu liegen.
Bauprinzip
Vorgehen
des
Aneinanderreihens, wie
ment der Faltbarkeit in der Ebene
es
im Falle des Rhombus als Grundele¬
angewendet wurde, wird hier auf den
Raum
übertragen.
Wie oben ersichtlich wurde, bilden die Ecken B, C, D, E der räumlichen
Figur
Quadrat parallel zur Referenzebene TT, so dass das Aneinanderreihen der
räumlichen Figuren in einem Netz von Quadraten parallel zur Ebene TT möglich
ein
ist.
\
r*v
111-30
GRUNDELEMENT DER FALTBARKEIT IM RAUM MIT VIERECKIGER PROJEKTION AUF DIE
REFERENZEBENE TT
Figur
In der oben beschriebenen
Stäbe ersetzt und mit Gelenken
lenkanschlüssen senkrecht
jeweilige
Seite und die
werden die Seiten durch acht
verbunden,
Diagonale
ben die Stabketten AB, BF, FD, DE
dass die Drehachsen in den Ge¬
stehen, die gebildet wird durch die
der Ebene
zu
so
gleich lange
AF der
ursprünglichen Figur. Dadurch blei¬
bzw. AC, CF, FE, EA je parallel zu einer
Ebene.
Der-Freiheitsgrad
F
g1
folgt
des Gebildes kann wie
=
3(n-l)
2(g
-
ist die Anzahl der Gelenke mit f
=
+
ermittelt werden:
3g3)
1 und einfacher
Wertigkeit
(zwei anschliessende Stäbe)
g
ist die Anzahl der Gelenke mit f
F
F
Es handelt sich
um
einen
=
=
3(8-1)
=
-
Wertigkeit
(vier anschliessende Stäbe)
1 und dreifacher
2(4
+
3-2)
=
1
1
zwangsläufigen Mechanismus.
111-31
folgende Photosequenz zeigt die Entfaltung eines faltbaren Modularen
Grundelementes mit quadratischer Projektion auf die Referenzebene TT am
Die
Modell, in Auf- und Seitensicht.
Bild 1:
Das
a
=
gefaltete
Modell
0
Bild 2:
Zwischenstadium
der Entfaltung
VJ
5ild 3:
Endstadium der Ent¬
faltung.
Das ent¬
faltete Modell.
Sämtliche Knoten
liegen auf der Ebene
a
=
tt
TT
111-32
Beispiele des vorher beschriebenen räumlichen Modularen Grundelementes mit
quadratischer Projektion auf die Referenzebene
Wie vorher im Abschnitt 'Modulares
TT
Bauprinzip' beschrieben,
ist
möglich,
Gruppierung zu bilden,
in einem Quadratrasterfeld liegt.
es
durch Aneinanderreihen der räumlichen Elemente eine
deren
Projektion auf die Referenzebene
TT
X
\
/\
^
^
^
Betrachten wir die beiden benachbarten Elemente ABCDEF und DGHIJK, die durch
den Knoten D miteinander verbunden sind. Sie
renzebene
länge
a'
Elemente
TT
=
als zwei
V2
a
gleiche Quadrate B'C'D'E' und D'H'I'J' mit der Seiten¬
sina/2,
gleich ist.
projizieren sich auf die Refe¬
wobei
a
als Parameter der Transformation für beide
111-33
a/2
2
7^\
y<-
Aufgrund einfacher geometrischer Ueberlegungen wird ersichtlich, dass der
Stab AD auf der Verlängerung des Stabes DK liegt, ebenso der Stab FD auf
Verlängerung von DG. So können die beiden Stäbe AD und DK bzw. FD und
durch die durchgehenden Stäbe AK und FG ersetzt werden, die in D gelenkig
der
DG
miteinander verbunden sind.
El^i^fi£§2£5§®_5® „^sjneh^r^^Mo^u^are^G^undelementen_zusammengese tz ten
Mechanismus
Das Problem wird im
folgenden anhand des oben beschriebenen Beispiels
er¬
läutert :
Gegeben
sei das oben
dargestellte
aus
vier Modularen Grundelementen
gesetzte Gebilde, bei welchem die mittleren Stäbe, die in
durchgehend
D
zusammen¬
zusammenlaufen,
sind.
diejenigen Drehgelenkkombinationen zu ermitteln, die bei einer
Anzahl Stabanschlüsse noch einen zwangsläufigen Mechanismus er¬
Versuchen wir
minimalen
geben (F
=
1)
.
(Anzahl Stäbe)
n
=
28
3
£
gi
(Anzahl Drehgelenke,
besitzt)
wenn
jeder Stab mindestens zwei Gelenkanschlüsse
111-34
ergeben sich zwei verschiedene Gelenkkombinationen:
Es
FALL A
3
£
i=l
g.1
=17 (Kombination mit einem Gelenk in D)
g.
=16 (Kombination ohne Gelenk in D)
FALL B
3
I
i=l
Der
Freiheitsgrad
F
wobei:
g
g„
g..
folgt
kann wie
=
3(n-l)
-
2(gx
ermittelt werden:
+
2
g2
+
g3)
3
=
Anzahl der Gelenke mit einfacher
=
Anzahl der Gelenke mit zweifacher
=
Wertigkeit (2 anschliessende
Stäbe)
Anzahl der Gelenke mit dreifacher
Wertigkeit (3
anschliessende
Stäbe)
Wertigkeit (4 anschliessende
Stäbe)
untersucht, für den gilt:
Zuerst wird der Fall A
F
1
=
3
Ig,1
I)
=
17
i=l
II)
1
=
1
=
23
=
3
(28-1)
3-27
g2
+
-
2
-
2(gx+ 2
2 ( E
i=l
9l+ g2
3
+
g2
+
2
g3)
g3)
g3
Bedingung:
g.
_>
4, weil in jedem Stab mindestens zwei Gelenkanschlüsse vorhanden sein
sollen (betrifft die Knoten B, N, I, Q; siehe Abb., S. 111-32)
sowie:
g
>
Für g
0
und g
=
_>
0.
4 erhält
g2
g3
g1
g2
g3
man
aus
=
3
=
io
=
=
=
I und II:
B, I, N,
Q
A, G, M
C, D, E, F, H, J, K, L, O, P
111-35
Für g
=
5:
g2
g3
g±
g2
g3
=
i
=
n
=
B, D, I, N, Q
=
G
=
A, C, E, F, H, J, K, L, M, O, P
gn =6:
Für
g2
<o
Nun untersuchen wir den Fall B, für den
F
1
=
Ig.X
I)
gilt:
16
=
i=l
1
=
3(28-1)
1
=
3-27
-
2(gx
2 ( I g,
l
1=1
-
2
+
+
...
1
24
II)
81
=
2
g3
>_
0
+
g2
=
2 (16
-
+
g2
g2
g,+
2
+
2
3
+
2
g3)
g.)
3
g3)
Uebrige Bedingungen:
g
>
4
Für g
sowie
=
j>
0 und
g
4
I
Aus II
g
->
und III
III)
g2
+
g3
=
12
ergibt sich:
g2
g3
g±
g
=
=
o
i2
=
B, I, N, Q
=
A, C, D, E, F, H, U, K, L, M, 0, P
111-36
Für g
=
5
i
+
g2
-
I und II
g3
->-
=
g„
^2
ll
<
0
Zusammenfassend:
ergibt zwei mögliche Varianten:
FALL A: Mechanismus mit 17 Knoten
Al
"**
gi
A2
"*"
gl
=
4'
g2
=
5'
g2
=
3'
g3
=
1'
g3
=
10
=
1X
=
12
FALL B: Mechanismus mit 16 Knoten:
B,
Die
-
gx
=
vorhergehenden
4,
g2
=
0,
g3
Gelenkkombinationen
Zwangsläufigkeit
minimalen Anzahl Stabanschlüsse die
erhalten bleibt.
Analog
zum
zeigen die Fälle, in denen bei einer
Beispiel
von
des Mechanismus noch
Seite 111-12 kann die
Gelenkwertig¬
keit bis auf
g±
=4,
g2
=
0,
g3
=
13
erhöht werden, ohne dass der Mechanismus seine
Zwangsläufigkeit verliert,
d.h., man kann alle Stäbe, die sich jeweils in einem
Drehgelenke miteinander verbinden.
Knoten
treffen, durch
111-37
folgenden zwei Beispiele zeigen die Möglichkeiten der Ausbildung
faltbaren Raumfachwerken aufgrund des Modularen Bauprinzips.
Die
Beispiel
1
Durch Aneinanderreihen können die Modularen Grundelemente in ein
Rasternetz
den
von
parallel
zur
Ebene
TT
gebracht werden,
so
quadratisches
dass die Stäbe, die
an
Berührungspunkten zweier benachbarter Elemente zusammenstossen und auf
einer Linie liegen, als ein einziger durchlaufender Stab ausgebildet werden.
III-3c
Bei diesem
Beispiel handelt
es
sich
um
eine Struktur, die
aus
Grundelementen besteht.
Aufsicht auf ein Modulares Grundelement:
Aneinander
gereihte
%
Y\
Modulare Grundelemente in der Aufsicht:
fi^
9
%1
S
B
25 Modularen
111-39
Die
folgende Photosequenz zeigt
die durch Aneinanderreihen
jektion
Entfaltung
einer räumlichen
Modularen Grundelementen mit
von
auf die Referenzebene
die
TT
Struktur,
viereckiger
Pro¬
entstanden ist.
Bild 1:
Das
gefaltete
Modell
Bild 2:
Anfangsstadium der
Entfaltung
Bild 3:
M
m
Zwischenstadium der
m'&
Entfaltung
m
M aMi
111-40
Bild 4:
anm K a
^
mVa
m
^m *ü m
gi
¦/.
m
*«
m
mm
ss
Das beinahe entfaltete
Modell
Wk\ WA
m
s
Bild 5:-Das entfaltete Modell.
Endstadium der Ent¬
faltung.
111-41
Beispiel
Das
2
folgende Beispiel
Weise werden
zum
ist eine
Ergänzung
Mechanismus Stäbe und
entfaltetem Zustand als Ober- und
Beispiel 1. Auf zweckmässige
Knoten hinzugefügt, so dass sie bei
zum
Untergurt
des
ursprünglichen Stabgebildes
dienen, ohne gegen die kinematische Verträglichkeit der Faltung
Beschreibung
des Grundmechanismus:
\/
v
7
\>
rz
H
v
V
</
er
/
/s
V
t
/
\
v
/
y>7
/D
zu
Verstössen.
111-42
Die Struktur besteht
aus
fünf Modularen Grundelementen mit
quadratischer
seien die zugehörigen Spitzknoten,
Projektion auf die Ebene TT. A, B, C, D, E
die so angeordnet sind, dass A das Zentrum und B, C, D, E die Ecken eines
2 a sina/2 bilden. Ergänzen wir das Ge¬
Quadrates mit der'Seitenlänge 1
bilde durch Einführen der Stäbe FB, FC, FD, FE mit der Länge b, und unter¬
=
suchen wir den Einfluss der vier
des
neuen
Stäbe auf das kinematische Verhalten
ursprünglichen Mechanismus.
vorgängigen Beispiel ersichtlich wurde, ist der Mechanismus des
aus fünf Modularen Grundelementen gebildeten Systems zwangsläufig, d.h.:
Aendert der Parameter, so bewegen sich die Punkte B, C, D, E bezüglich A
Wie
aus
auf
gradlinigen
Dabei
dem
von
A.
gilt:
AB
AC
=
AD
den, der
lich der
AE
t/J
=
a
sina/2
dargestellt wer¬
alle geometrischen Bedingungen des ursprünglichen Modells bezüg¬
relativen Bewegung der Punkte B, C, D, E zueinander und bezüglich
Das Gebilde kann mit einem
ihrer
Richtung
Bahnen in die
neuen
Bewegung gegenüber Punkt
fiktiven Hilfsmechanismus
A erfüllt:
/\
\7l
^
\
J
c/
\
\
\
>5^
P
/ /
\
//
\
//
*n u
*
//
i
111-43
F
F
Die
(gi
=
3(n-l)
-
2
=
3(8-1)
-
2 (4
Zwangsläufigkeit
3
-
+
g2)
3-2)
1
=
des Gebildes bleibt erhalten.
beweisen, dass die Zwangsläufigkeit des Mechanismus auch
erhalten bleibt, wenn in die Figur die Stäbe B'F', C'F', D'F', E'F', die
symmetrisch zu BF, CF, DF, EF sind, und die die Länge b haben, eingefügt
Analog
kann
man
werden.
Aus
geometrischen Ueberlegungen wird ersichtlich, dass:
FÄ
•b2 -2a2 sin2a/2'
=
Dadurch erhalten wir zwei Grenzfälle:
Für
I)
a
=
0°
FÄ
ist
b.
=
Die Stäbe BF, CF, DF, EF kommen auf eine Linie
Struktur ist
II)
=
0 ist FA
bedeutet, dass sich der
Das
liegen, d.h., die
zusammengefaltet.
(b2 -2a2 sina/2)
Für
zu
0.
=
Stäbe BF, CF, DF, EF in einer Ebene
diesem Fall ist
a
2 aresin
=
deckt, und die
Knoten F mit dem Knoten A
parallel
b/^2*a
zur
Ebene
TT
liegen.
In
und die Struktur ist voll ent¬
faltet.
Die Funktion
a
und b
ergibt folgende geometrische Verträglichkeitsbedingung zwischen
:
——
/TU
<
1
->
b
<
/T~ä
Damit die Möglichkeit der Kraftübertragung zwischen den Knoten A und A' be¬
steht,
müssen sie miteinander verbunden werden.
Biegebeanspruchung geeignet,
Teil aus diagonal gerichteten
Diese Struktur ist im entfalteten Zustand für
Obergurt,
indem sie einen
Stäben und einen
einen mittleren
Untergurt hat,
wobei die drei Schichten untereinander
weils schubfest verbunden sein müssen.
je¬
111-44
Die
folgende Photosequenz zeigt die Entfaltung einer
auf dem beschriebenen
Prinzip beruht,
Struktur
am
Modell, die
in Aufsicht und Seitensicht.
Bild 1:
Das
gefaltete Modell
Sg
m
m
s
'&fc
»
fr« 1
8
&
MS
ii
n
Bild 2:
PI
Im
Wi
3»sm
SS
H
a
Enfaltung
Bild 3:
Das entfaltete Modell
in Aufsicht
SHI
Hl m
88
Zwischenstadium der'
Hl
111-45
Bild 4:
Das
1 1
i
i
gefaltete Modell
Bild 5:
i
Zwischenstadium der
Entfaltung
a
Bild 6:
Das entfaltete
i
Modell
in Seitenansicht
111-46
MODULARES GRUNDELEMENT MIT SECHSECKIGER PROJEKTION AUF DIE REFERENZEBENE TT
Nehmen wir drei identische
übereinanderliegende
Seitenlänge
Rhomben mit der
und den Ecken A, B, H, E bzw. A, C, H, F bzw. A, G, H, D und der
a
gemeinsamen
Diagonalen AH. Wird nun ein Rhombus um 60° und ein zweiter um 120 um die
Diagonale AH gedreht, so entsteht eine räumliche Figur mit den Ecken A, B,
C, D, E, F, G,
H:
/\
20*
60*
Analog
zum
quadratischer Projektion auf die
Winkel a zwischen zwei benachbarten koplanaren
Modularen Grundelement mit
Referenzebene
tt
können wir den
Seiten ändern und dadurch den Abstand der zwei
gegenüberliegenden
Ecken
ver-
grössern bzw. verkleinern.
So kommen die Ecken B,
C, D, E, F, G in eine Ebene parallel
zur
Referenzebene
111-47
TT
liegen;
zu
ihre
Seitenlänge a'
Für
a
=
0
=
Projektionen auf
a
wird das Sechseck BCDEFG
TT
reguläres
Sechseck mit der
zu
Segmente der
einem Punkt. Alle
auf einer Linie senkrecht
Ebene
zur
ur¬
TT.
Bauprinzip
Modulares
ebene
bilden ein
sina/2.
sprünglichen Figur liegen
Analog
TT
zum
Fall des Elementes mit
bleibt die
quadratischer Projektion auf die Referenz-
Projektion eines Grundelementes auf
der Ebene TT während
Faltvorganges ein reguläres Sechseck. So ist es möglich, durch Aneinan¬
derreihen eine Gruppierung zu bilden, deren Projektion auf die Referenz¬
ebene TT ein Rasternetz ergibt, das aus regulären Sechsecken besteht.
des
111-48
GRUNDELEMENT FUER DIE FALTBARKEIT IM RAUM MIT SECHSECKIGER PROJEKTION AUF
DIE REFERENZEBENE TT
Wir ersetzen die Seiten der oben beschriebenen Grundelemente durch 12
gleich
Drehgelenke,
lange
zu derjenigen Ebene stehen, die durch die betreffende Seite und die Diago¬
nale AH der ursprünglichen Figur gebildet wird. So entstehen drei ebene
Stäbe und verbinden diese durch
viergliedrige
deren Drehachsen senkrecht
Stabketten:
AB, BH, HE, EA bzw. AC, CH, HF, FA bzw. AD, DH, HG, GA.
Der
Freiheitsgrad
F
dieses Gebildes kann wie
wobei:
g
=
6
=
=
2
=
=
3 (n-l)
2
-
(g
+
5
folgt ermittelt werden:
g5)
Anzahl der Gelenke mit f
=
1 und einfacher
Wertigkeit
(zwei anschliessende Stäbe)
g^
Anzahl der Gelenke mit f
=
1 und fünffächer
Wertigkeit
(sechs anschliessende Stäbe)
Es handelt sich
F
=
3 (12-1)
F
=
1
um
einen
-
2 (6
+
5-2)
zwangsläufigen
Mechanismus.
111-49
folgende Photosequenz zeigt die Entfaltung
Grundelementes mit sechseckiger Projektion auf
Die
eines faltbaren Modularen
die Referenzebene TT
am
Modell in Auf- und Seitensicht.
Bilder 1 und 2:
Das
gefaltete Modell
t
Bilder 5 und 6:
Zwischenstadium der
Entfaltung
Bilder 7 und 8:
Endstadium der Ent¬
faltung.
Das ent¬
faltete Modell.
Sämtliche Knoten der
Struktur liegen auf
der Referenzebene
TT
111-50
MODULARES GRUNDELEMENT MIT DREIECKIGER PROJEKTION AUF DIE REFERENZEBENE TT
Ausgehend
vom
Referenzebene
Modularen Grundelement mit
sechseckiger Projektion
auf die
verändern wir die
ursprüngliche räumliche Figur dadurch,
dass wir die alternierenden Seitenpaare AB, BH, AD, DH, AF, FH entfernen.
TT
/\
zr
Figur projiziert sich auf
Dreieck mit der Seitenlänge a1
v3
Diese
neue
=
Im Sinne des Modularen
können wir diese
der Ecken der
liegen,
das
neuen
die Referenzebene
a
als
gleichseitiges
sina/2.
Bauprinzips und analog zu den vorhergehenden Fällen
Elemente so aneinanderreihen, dass die Projektionen
Figuren (B, D, F) auf die Referenzebene
aus
TT
regulären
Dreiecken
gebildet
ist.
TT
"•
in einem Rasternetz
111-51
MODULARES GRUNDELEMENT DER FALTBARKEIT IM RAUM MIT DREIECKIGER PROJEKTION
AUF DIE REFERENZEBENE TT
Analog
zum
vorangehenden Fall erhalten wir dadurch, dass wir die Segmente
durch Stäbe ersetzen, die mit
Drehgelenken
verbunden sind,
folgenden Mechanis¬
mus:
Der
Freiheitsgrad
F
wobei: g
=
folgt ermittelt werden:
des Mechanismus kann wie
=
3
(n-l)
-
2
(g
2 g )
+
Anzahl der Gelenke mit f
=
1 und einfacher
Wertigkeit
(zwei anschliessende Stäbe)
g
=
doppelter Wertigkeit
(drei anschliessende Stäbe)
Anzahl der Gelenke mit f
F
=
3
F
=
1
(6-1)
-
2 (3
+
=
1 und
2-2)
=
1
111-52
Die
folgende Photosequenz zeigt
mit
dreieckiger Projektion
die
Entfaltung eines Modularen
auf die Referenzebene
TT
Grundelementes
anhand eines Modelles in
Seiten- und Aufsicht.
Bilder 1 und 2:
Gefaltetes Modell
Bilder 5 und 6:
Zwischenstadium der
Entfaltung
S
Bilder 7 und 8:
Endstadium der
Entfaltung.
Das entfaltete Modell.
Sämtliche Knoten des
Modells liegen auf
der Ebene TT
111-53
Beispiel
Hinzufügen von Modularen Grundelementen analog der Gruppierung im
vorherigen Beispiel können wir die Struktur parallel zur Ebene TT in beide
Richtungen ausdehnen, so dass das folgende faltbare Gebilde auf der Basis
Durch
eines 60 -Rasters entsteht.
111-54
folgende Photosequenz zeigt
Die
wird
ebene
aus
TT
die
Entfaltung
Modularen Grundelementen mit
einer
Struktur, die gebildet
dreieckiger Projektion
auf die Referenz¬
in Aufsicht und Seitenansicht.
Bild 1:
Das
gefaltete
Modell
*4 *fe*l#
m
EXE
wpsrtrani
^S^3SF^tS
RS^B>9
90
£
Bild 2:
Zwischenstadium der
Entfaltung
91
^
^i
s ÄH
M
^SB
Bild 3:
US
^
fi
Das entfaltete Modell
in Aufsicht
111-55
Bild 4:
Das
s
BF«^
ii
//.
i
gefaltete Modell
:Bild 5:
1
s m
S
Wa m
Zwischenstadium der
Entfaltung
3
m
Bild 6:
-
Das entfaltete
in Seitensicht
Modell
IV Prinzipien der Faltbarkeit
mit Polyedern als Grundelementen
IV-1
Prinzipien der Faltbarkeit mit Polyedern als Grundelementen
Weitere
der Faltbarkeit räumlicher
Prinzipien
Tragwerke können aufgrund
von
Eigenschaften der Polyeder ermittelt werden.
Die
Untersuchung dieses Gebietes führt
Polyeder
1. An das betrachtete
Seiten des
zu
den
folgenden Feststellungen:
assoziieren wir eine
Polyeders in Stäbe und die Ecken in
Struktur, bei der die
Knoten
umgewandelt
wer¬
den.
Ausgangsstruktur unter Berücksichtigung
ihrer geometrischen und kinematischen Verträglichkeitsbedingungen in ein
faltbares Gebilde umgewandelt, d.h. es kommen alle Stäbe der Struktur
2. Durch Transformation wird die
parallel zueinander
3. Das
neu
zu
liegen.
entstandene Gebilde soll
derreihen
von
so
beschaffen sein, dass durch Aneinan¬
einzelnen Elementen im Sinne des Modularen
Bauprinzips
komplexere Strukturen entstehen können, die ihrerseits auch faltbar sind.
Im
folgenden Abschnitt werden wir zwei verschiedene Polyeder untersuchen:
das vierfach
abgestumpfte
Aus dem vierfach
faltbare Struktur
Oktaeder und den Würfel.
Oktaeder als Grundelement lässt sich eine
abgestumpften
bilden,
von
der wir mehrere der im
vorherigen Kapitel
beschriebenen räumlichen Strukturen ableiten können.
ergibt einen Grundmodul zur Faltung ebener sowie räumlicher Fach¬
werke, wobei sich der Faltvorgang auf andere Gebilde übertragen lässt, die
ihrerseits Grundelemente zur Faltung weiterer Typen ebener und räumlicher
Der Würfel
Fachwerke sind.
ab, durch zweckmässige Kombination
solcher Grundelemente faltbare sphärische Fachwerke zu bilden.
Letztlich zielt dieses
Vorgehen
darauf
IV-2
DAS VIERFACH ABGESTUMPFTE OKTAEDER ALS GRUNDELEMENT DER FALTBARKEIT IM RAUM
geschaffen, aus dem
gebildet werden können.
In diesem Abschnitt wird ein faltbares Element
Aneinanderreihen faltbare Raumfachwerke
Betrachten wir ein Oktaeder mit einer
Raumdiagonalen
senkrecht
zur
r-
>
\>
77
durch
Ebene
TT:
IV-3
Das Oktaeder wird
Ebene
TT
so
an
den Ecken B, C, D und E durch Ebenen senkrecht
abgestumpft,
dass die
jeweiligen Seiten BC, CD,
zur
DE und EB hal¬
biert werden.
A
rs
\D
%
i<?
•v
1^7
\<J
'>
Xy
Seitenlänge a/2 und den Spitzen
ein weiteres Polyeder mit den folgenden geometrischen
Dadurch entstehen vier
B, C, D und E sowie
¦X\
Pyramiden
mit der
Elementen:
Anzahl Ecken:
14
Anzahl Seiten:
24
Anzahl Flächen:
12,
wovon
4
Ersetzen wir die Kanten des
Gelenke verbunden sind
,
Quadrate und 8 Rhomben.
Polyeders durch Stäbe, die in den Ecken durch
IV-4
erhalten wir einen räumlichen Mechanismus, dessen
folgt ermittelt werden kann:
so
F
wobei:
=
3g
n
-
-
Anzahl Knoten
n
=
Anzahl Stäbe
F
=
3-14
Es handelt sich
-
um
wie
6,
=
g
Freiheitsgrad
24
6
-
=
12
einen räumlichen Mechanismus mit 12
Tranformation 1: Vom räumlichen
zum
Freiheitsgraden.
ebenen Gebilde
VM
m
oß
/N
Bewegen wir den Knoten
schen
N
Einhaltung
A unter
gegen
der
folgenden geometri¬
Bedingungen:
bewegt
I
N
II
Die Winkel BAN
=
CAN
=
DAN
=
JNA
=
KNA
=
LNA
=
sowie
sich
entlang der Raumdiagonalen
EAN
MNA
=
a/2
=
a/2
AN gegen A.
IV-5
Die
geometrischen Bedingungen
I und II
widerspiegeln
sich in den kinemati¬
schen
Bedingungen, indem sie die Freiheitsgrade wie folgt beschränken:
I)
¦>
F*
=
-2
II)
->
F'
=
-8
Der
gesamte Freiheitsgrad ist:
F
III)
=
12 -2-8=2
Nehmen wir den Winkel
wie
von a
2
AN
Mit dieser
F
a
folgt
als Parameter,
lässt sich AN als Funktion
so
ausdrücken:
cosa/2
Bedingung
=
a
wird der
gesamte Freiheitsgrad
um
eins reduziert:
1
Der Mechanismus wird
zwangsläufig.
Ausgangsposition ist a
TT/2. Für a TT ist der Abstand AN 0.
Sämtliche Punkte der Figur befinden sich in der Ebene TT und bilden ein Quadrat
mit der Seitenlänge a, dessen Zentrum mit den Mittelpunkten der Seiten ver¬
bunden ist. Zudem ist in dieser Position die Lage von A und N bzw. B und J
In der
bzw. C und K bzw. D und L bzw.
=
=
E und M
=
identisch.
17
IV-6
Man
beachte, dass sich die Figur während des ganzen Faltvorgangs als Quadrat
mit der Seite 1
Die
=
a
sina/2
auf die Ebene
folgende Photosequenz zeigt
vorgangs
am
projiziert.
Für
a
=
TT
ist 1
=
a.
die Struktur des vorher beschriebenen Falt¬
Modell:
Bild 1:
Das abgestumpfte
in Seitensicht
Polyeder
Bild 2:
Verschiebung
des Knotens
Raumdia¬
entlang der
gonalen AF
F
^^
IV-7
Bild 3:
Zwischenstadium des
Faltvorgangs
Bild 4:
||^*
Der Knoten F deckt sich
mit dem Knoten A, und
die Seiten der ur¬
sprünglichen Figur lie¬
gen in der Ebene TT
IV-8
Transformation 2: Vom ebenen
Gehen wir
linearen Gebilde
zum
der Position aus, in der alle Punkte der
von
Fassen wir die Knoten A und N
liegen.
Bewegung
der Knoten
Die Knoten
A', F, G,
bezüglich der
Ebene TT:
H und I bleiben in der Ebene TT.
bzw. B, C, D, E entfernen sich in
o
zu
Figur auf der Ebene TT
einem einzigen Knoten A' zusammen.
Die Knoten J, K, L, M
entgegengesetzter Richtung
von
der Ebene TT.
<K
0on
w
^
77
¦Dieser
Bewegung wird zusätzlich folgende Bedingung zugrunde gelegt:
Der Winkel zwischen der Senkrechten zu TT in A' und den Segmenten A'B, A'C,
A'D, A'E bzw. A'J, A'K, A'L, A'M soll jeweils gleich sein.
Die ganze Transformation kann in
Abhängigkeit
vom
Winkel
ausgedrückt
a
wer¬
den:
Seien
...
auf die Ebene TT,
erhalten wir:
so
d
B', C, D',... Projektionen der Punkte B, C, D,
=
für
A'B'
a
=
=
0,
A'C
d
=
=
'n'
A'D
=
jit-i
A'E'
A'J'
0 ist. D.h. sämtliche
auf eine Strecke
zu
liegen.
=
A'K'
=
A'L'
=
A'M'
=
%r2
sin
~J-"
%2
,
so
dass
Segmente der ursprünglichen Figur kommen
IV-9
Die
folgende Photoserie zeigt
den vorher beschriebnen
Faltvorgang
am
Modell:
Bild 1:
Alle Knoten der
liegen
Figur
auf der Ebene
TT
Bild 2:
Zwischenstadium
der
Faltung
i»
Bild 3:
gefaltete'
Figur
Die beinahe
räumliche
1
IV-10
Halten wir fest, dass sich die
ursprünglich räumliche Figur durch eine
räum¬
liche Transformation in ein ebenes Gebilde und durch eine weitere räumliche
Transformation in ein lineares Gebilde verwandelt hat.
Darstellung der ummantelnden Fläche für die zweite Phase des Faltvorgangs:
Vom ebenen
zum
linearen Gebilde:
IV-11
Da die beiden
ursprünglichen Endpunkte der Raumdiagonalen
sammenfallen, sind die Stäbe NJ, NK,
AE des
NL und NM bzw.
ursprünglichen polyedrischen Gebildes
A und N in A'
die Stäbe AB,
zu¬
AC, AD und
in der zweiten Phase des Faltvor¬
gangs in A' miteinander verbunden.
Zudem
folgt
aus
der
Abhängigkeit
des
gesamten Faltvorgangs
vom
Parameter a,
dass die Stäbe A'B und A'L bzw. A'C und A'M bzw. A'D und A'J bzw. A'E und A'K
in der zweiten Phase des
Faltvorgangs auf eine Strecke mit der Länge a und
dem Mittelpunkt A' zu liegen kommen. Entsprechend können sie jeweils durch
einen einzigen Stab BL bzw. CM bzw DJ bzw. EK, der durch A" geht, ersetzt
werden.
Bild 1:
beachte, dass die
Stäbe im Zentralknoten A'
Man
durchgehend ausgebildet
sind.
Bild 2:
Der Knoten A' in der
Aufsicht
IV-12
Die
folgende Photoserie zeigt
drei Stadien der
Entfaltung
der Struktur in
Auf- und Seitensicht:
m
HS
K
iM:
r^i
L J
I
IV-13
Vergleich der vorangehend behandelten faltbaren
Struktur mit dem auf Seite
111-28 definierten faltbaren räumlichen Grundelement mit
jektion auf die Ebene
Man
Projektion auf
Pro¬
TT
beachte, dass die
bare Struktur sich
quadratischer
teilweise
aus
vom
abgestumpften
Oktaeder
abgeleitete falt¬
einzelnen räumlichen Grundelementen mit
die Ebene
TT
quadratischer
zusammensetzt.
\
CU
—
tjf
n
71
u
¦^
y
\
\
--O
7
IV-14
Die
folgenden Photos zeigen die beiden
Man beachte die
Strukturen in Auf- und Seitensicht.
Analogie zwischen den Teilen
der beiden Modularen Grund¬
elemente.
52
r~i
IV-15
Vergleich
Indem
die
abgestumpften
des teilweise
man vom
Rhombododekaeder
Oktaeders mit dem Rhombododekaeder
ausgeht, kann
durch ein ähnliches Verfahren
man
gleiche faltbare Struktur erzeugen wie sie mit dem teilweise abgestumpften
Oktaeder erzeugt wurde.
Zusammenfassung der geometrischen Elemente des Rhombododekaeders:
Anzahl Ecken:
14
Anzahl Kanten: 24
.a
=
0.45970 D
(D
=
Durchmesser der umschriebenen
Sphäre)
Prinzip der Faltbarkeit:
Betrachten wir ein Rhombododekaeder mit der
in der Ebene TT,
so
dass eine
Raumdiagonale
Seitenlänge
AN senkrecht
Ersetzen wir die Kanten des Rhombododekaeders durch
a
und mit der Ecke A
zur
Ebene
TT
steht.
Stäbe, die in den Ecken
gelenkig miteinander verbunden sind. Verschieben wir die Ecke N entlang der
Raumdiagonalen AN gegen die Ecke A, bis sämtliche Teile des so entstandenen
Gebildes auf der Ebene TT
liegen
und ein
Ecken F, G, H und I und dem Zentrum N
stadium der
=
Quadrat
mit der
Seitenlänge 2a,
den
A bilden. Man beachte: Dieses Zwischen¬
Faltung ist mit demjenigen des im vorhergehenden Abschnitt be¬
schriebenen, vom Oktaeder abgeleiteten Grundelementes identisch.
IV-16
1
Für die zweite Phase des
schaften.
Faltvorgangs gelten sie vorher ermittelten Eigen¬
IV-17
DER KUBUS ALS GRUNDELEMENT DER FALTBARKEIT
Betrachten wir einen Kubus ABCDEFGH mit der
der Ebene
TT
und der
Raumdiagonalen
Seitenlänge
AH senkrecht
Projektion dieses Würfels auf die Ebene
TT
a, der Ecke A in
Ebene TT. Der Umriss der
zur
bildet ein
reguläres
Sechseck.
/\
<s
Li
>
z\
Ersetzen wir die Kanten des
Polyeders durch Stäbe, die in den Ecken durch
Gelenke verbunden sind. Die so entstandene Struktur hat folgenden Freiheits¬
grad:
F
=
3g
n
-
g
(Anzahl Knoten)
=
n
(Anzahl Stäbe)
=
Es handelt sich
um
6
-
6
12
einen Mechanismus mit 6
Freiheitsgraden.
IV-18
Transformation 1: Vom räumlichen
ebenen Gebilde
zum
Bewegen wir den Knoten H gegen A unter Einhaltung folgender geometrischer
Bedingungen:
I
Der Knoten H
II
CAH
=
ÜJAH
=
bewegt
GAH
=
sich
entlang der Raumdiagonalen
a, wobei
a
entsprechend
AH gegen A.
dem Abstand AH variiert.
eingeführten geometrischen Bedingungen bringen eine Beschränkung des
Freiheitsgrades mit sich. Sie wirken sich wie folgt auf die kinematischen
Die
Bedingungen
I
F'
II
FB
Der
aus:
-2
=
-3
=
gesamte Freiheitsgrad
F
6-2-3
=
Der Mechanismus wird
vom
Parameter
=
ist:
l
zwangsläufig;
damit
a:
AH
AB'
=
B'C
=
Das
ÄC
CD'
ergibt sich folgende Abhängigkeit
DD'
=
FF'
=
EE~'
=
GG'
AD'
=
Äe"'
=
ÄF'
=
D'E'
=
E'F'
=
F'C
=
BB'
=
CC"'
=
=
3
a
cosa
2
a
cosa
a
cosa
=
a
sina
=
a
sina
=
=
ÄG'
G'B'
bedeutet, dass der Umriss der Projektion der
auf die Ebene TT ein
trum in A
ergibt.
reguläres
Sechseck mit
B, C, D, E, F, G
Knoten
Seitenlänge
a'
=
a
sina und Zen¬
IV-19
Durch
die
Aenderung
des Parameters
Längen AB', BB', CC und
a
erhält
HA:
0°
35.2643°
AB'
0
0.5773
a
0.8160
a
a
CC'
a
0.8160
a
0.5773
a
0
a
.
54.7355°
,
90°
b¥'
2
a
1.6329
a
1.1547
a
0
HA
3
a
2.4494
a
1.7320
a
0
/\
CUBUS
3a
HA
2a
CC
folgende numerische
man
/
AB
L
54,7355'
90"
Werte für
IV-19a
0, AB' =0, BB'
Für
a
der
ursprünglichen
Für
a
=
=
90°,
AB'
=
=
Struktur
a,
AB'
CC'
a,
=
=
2a, HA
parallel
BB'
der Struktur auf der Ebene TT;
=
der
CC'
um
=
=
ein
HA
3a, d.h.
es
0, d.h.
es
liegen alle Stäbe
Segment mit der Länge 3a gruppiert.
=
ursprüngliche
liegen
alle Stäbe
Kubus ist in ein
reguläres
Sechseck mit Seite a, den Ecken
B,C,D,E,F,G und Zentrum in den zwei überei¬
nanderliegenden
übergegangen.
Die
Punkten
A und H
folgende Photoserie zeigt den
oben beschriebenen
Faltvorgang
am
Modell:
Bild 1:
Die Struktur in ihrer
Ausgangslage
Bild 2:
Verschiebung des Knotens
H entlang der Raumdia¬
gonalen AH in Richtung A
IV-20
Bild 3
Bild 4:
Die Stäbe des Würfels
sowie der Knoten H zu.sammen mit dem Knoten A
•
kommen in die Ebene TT
zu liegen und bilden dort
ein reguläres Sechseck
Transformation 2: Vom ebenen
Indem wir
von
linearen Gebilde
zum
Kubus auf der Ebene
TT
bei der alle Stäbe des
ausgehen,
liegen, können
der Position
ursprünglichen
wir eine Transformation
ausführen, die
folgende Bedingungen erfüllt:
1. Der Knoten A bleibt fest in der Ebene
2. Die Knoten B, D und
3.
F
bleiben in der Ebene
Der Knoten H entfernt sich
lichen Kubus.
TT.
von
A
entlang
TT
der
verschiebbar.
Raumdiagonalen
des
ursprüng¬
IV-21
Ausgangslage
der
Transformation 2.
Alle Knoten liegen
auf der Ebene TT.
Die Stäbe bilden ein
Sechseck mit seinen
Radien
geometrischen Bedingungen II) und III) wirken sich auf die kinematischen
Bedingungen aus, indem sie den Freiheitsgrad des Mechanismus wie folgt be¬
Die
schränken:
II
F'
=
III
F'
=
gesamte Freiheitsgrad (ursprünglich F
Der
F
6-3-2
=
Der Mechanismus ist
=
AH
CC
AB
AC
BC
CD
=
EE'
6) wird
zu:
l
zwangsläufig.
ergibt sich folgende Abhängigkeit
So
=
=
GG'
=
AD
=
ÄF7
=
DE'
=
E'F
=
=
AG7"
FG7" Cb"
AF
=
=
vom
Parameter a:
=
a
cosa
=
a
sina
=
a
sina
heisst, der Umriss der Projektion der Knoten B, C, D, E, F, G auf die
Ebene TT ergibt ein reguläres Sechseck mit der Seitenlänge a'
a und dem
Das
=
Zentrum in A.
IV-22
~^
K
y
y
y
Durch die
a
AB
Aenderung des
90°
a
CC
HA
0
Parameters
45°
a
erhält
man:
35.2643°
0°
0.7071
a
0.5773
a
0
0.7071
a
0.8165
a
a
0.7071
a
0.8165
a
a
IV-23
Graphische Darstellung:
HA
BA FA DA GH....
Vi
90
45°
Für a
=
35.2643
3&26C
entsprechen die Punkte B, C, D, E, F,
Oktaeders mit der Seite
Für a
=
0
Die
a.
sind die Distanzen HC, HE,
und die Stäbe AC,
folgende
AE,
AG
Photoserie
G den Ecken eines
usw.
liegen
hg"
um
sowie auch
ÄB~, AD7,
gleich 0,
AF
eine Achse senkrecht
zur
zeigt den oben beschriebenen Faltvorgang
Ebene
am
TT.
Modell:
Bild 1:
Alle Stäbe und Knoten
liegen
a
=
90°
auf der Ebene
TT.
IV-24
Bild 2:
Die Knoten H, B, C und D
entfernen sich von der
Ebene
a ^
ti
70°
Bild 3:
a ^
45
Bild 4:
-a ^
.
25°
IV-25
Bild 5:
o
a ^ 0
Halten wir fest:
1. Das
ursprünglich räumliche
Modulare Grundelement lässt sich durch eine
räumliche Transformation in ein
ebenes, und durch eine weitere räumliche
Transformation in ein lineares Element umwandeln.
Faltungsprozesses bildet die Projektion des Grundele¬
mentes auf die Ebene TT unter Beibehaltung gewisser geometrischer Bedingun¬
gen immer ein reguläres Sechseck.
2. Während des ganzen
IV-26
Darstellung der ummantelnden Flächen in der zweiten Phase des Faltvorqancrs
(vom ebenen
zum
linearen Gebilde):
IV-27
ANWENDUNG DES PRINZIPS DER FALTBARKEIT DES WUERFELS
Bis anhin haben wir die
Faltvorgangs
geometrischen Eigenschaften des Würfels während
untersucht. Im
folgenden Abschnitt soll anhand
beispielen gezeigt werden, welche allgemeinen Eigenschaften
wir daraus ableiten
von
des
Anwendungs¬
der Faltbarkeit
können, und wie sich diese auf analoge geometrische Figuren
übertragen lassen.
Faltbarkeit
Bildung
von
ebenen Fachwerken
eines ebenen Fachwerkes auf der Basis eines
Beispiel
tion
Ebene
a
TT
Rasters:
1:
Betrachten wir das
=
sechseckigen
90
,
vom
Würfel
abgeleitete Modulare Grundelement
in der Posi¬
bei der sämtliche Ecken des
liegen,
so
dass sein Umriss ein
ursprünglichen Würfels in der
reguläres Sechseck mit der Seite
und dem Zentrum A und H bildet. Verbinden wir die Knoten A und H
und betrachten wir das
sechseckige
Gebilde als ebenes Fachwerk.
a
miteinander,
IV-28
Als ebener Mechanismus hat das Gebilde
folgenden Freiheitsgrad:
F f=1
E f=1
(H
f=1
ß f=1
F
=
2g
F
=
2*7
F
=
n
-
-
-
12
C f=1
3
-
3
-1
Das Gebilde ist stabil und hat eine
überzählige Bindung.
Trennen wir die miteinander verbundenen Knoten A und H,
das kinematische Schema und wir erhalten
n
=
12
g
=
8
F
F
F
3
=2-8-12-3
=
2g
=
1
-
n
-
so
verändert sich
folgenden Freiheitsgrad:
IV-29
Das Fachwerk ist als ebenes Gebilde instabil.
Während des weiteren
Ebene
zur
TT
liegen,
Faltvorgangs,
bei dem die Stäbe nicht mehr
parallel
kann das Gebilde als räumlicher Mechanismus betrachtet
werden.
Es hat
folgenden Freiheitsgrad:
12
n
=
g
=
F
=3g-n-6
F
=
8
3*8
-
12
-
6
=
6
Das gefaltete Gebilde
in der Aufsicht. Alle
Knoten und Stäbe liegen
um eine gemeinsame Achse
gruppiert.
Durch die
Aneinanderreihung
einzelner Elemente in einem
entsteht ein ebenes Fachwerk, das
mittleren Knotens in
sechseckigen
Raster
gefaltet werden kann, indem die Bindung des
jedem einzelnen sechseckigen Element aufgelöst wird.
IV-30
Die
folgende Photoserie zeigt
den beschriebenen
m
Faltvorgang
Modell:
am
Bild 1:
Das voll entfaltete
^m^.:
M
Modell. Teilansicht
Bild 2:
Anfangsstadium
i
%
I*ü
1S m
s m
Si
der
Faltung
s
Bild 3:
Zwischenstadium
der
Faltung
IV-31
Bild 4:
Das
¦
zusammengefaltete
Modell
folgenden Abbildungen vergleichen wir mit Hilfe eines Massstabes die
Ausdehnung der zusammengefalteten Struktur mit derjenigen der voll entfalteten
In den
Struktur:
J,
C-<
2»
Bild 5:
Das
zusammengefaltete
Modell
Bild 6:
0n
V.
Das beinahe entfaltete
Modell
IV-32
Beispiel
Am
2:
gleichen Grundelement wie in Beispiel
1 können die Stäbe
und CD entfernt werden; dadurch entsteht das
F f=1
E f=1
/
/v=l
\
/
\
\
/
B f=1
und weist keine
7
9
5
F
2g
F
2-5-7-3
F
0
-
n
-
=
7
g
=
6
F
=
3g
n
zum
-
n
\
w
/
\
r
-¥
c f=1
den Knoten A und H stabil
3
Durch Auflösen der
analog
;
Verbindung zwischen
überzähligen Bindungen auf.
Dieses ist bei bestehender
n
folgende Gebilde:
uu
f=1\
AB, AC, GB, BC
Bindung zwischen A und H erhält der räumliche Mechanismus
vorangehenden Beispiel folgenden Freiheitsgrad:
-
6
Das Gebilde kann
=3-6-7-6=5
gefaltet werden.
IV-33
Indem wir drei Elemente
aneinanderreihen, können wir ein ebenes Fachwerk bil¬
den, das faltbar ist:
Die
folgende Photosequenz zeigt die Struktur
am
Modell während des Faltvor¬
gangs :
Bild 1:
Die voll entfaltete
Struktur
r
IV-34
Bild 2:
Anfangsstadium
der
Faltung
Bild 3:
Wi
Die beinahe
Struktur
gefaltete
Bild 4:
Die
gefaltete Struktur
IV-35
Bildung eines faltbaren Raumfachwerkes durch Aufeinanderstappelung
von
Modularen Grundelementen
folgenden Abschnitt wird anhand eines Beispiels gezeigt, wie das Aufeinanderstappeln Modularer Grundelemente räumliche Gebilde entstehen lässt.
Im
Dieser Abschnitt bezieht sich auf den
Betrachten wir das
vom
Würfel
geometrischen
Aufbau des Fachwerks.
abgeleitete Modulare Grundelement während
Faltvorgangs:
y
^
y
K
y
y
%
y
des
IV-36
Nehmen wir ein
zweites, gleiches Grundelement und legen
es
so
auf das erste,
dass die Knoten A bzw. B bzw. D bzw. F des zweiten Elementes über die Knoten
H bzw. C bzw. E bzw. G des ersten
Die zwei
zu
liegen
jeweils übereinanderliegenden
E und D bzw.
F und G werden in einem
kommen.
Knoten A und H bzw. B und C bzw.
einzigen
Knoten miteinander verbunden.
Setzen wir den
usw.
Vorgang fort indem wir analog dazu noch ein drittes,
Element ankoppeln bis ein turmförmiges Gebilde entsteht.
^
<
y
P
\
t-
±
ök
/
y\
y
IE
y
*
y
y
ein
viertes,
IV-37
folgende Photoserie zeigt
SS
£
ti
$3**»—
3
-¦_
.
Die
die beschriebene Struktur
&V
SS
m
am
Modell:
Bild 1:
Die gefaltete Struktur in der
Aufsicht
i
Bild 2:
£^K
Anfangsstadium der Entfaltung.
Struktur in Seitensicht
IV-38
^
EWS5
iE
52
%^8 £Q
^"M^
US
*
KS
^mS S^
%
&
s
Bild 3:
Zwischenstadium der
Entfaltung
I
*gg X. m
K
s
ü
*
»
Ä
SS 7a
I
H
»
s
«
imI
8%
i
i11
I
m&S^
ft s
I
miI
«
K
Bild 4:
Die entfaltete Struktur
IV-39
GEOMETRISCHE BEDINGUNGEN DER FALTBARKEIT VON EBENEN SECHSECKIGEN GEBILDEN
Betrachten wir das
zweiten Phase des
vom
Würfel
Faltvorgangs
abgeleitete
vom
ebenen
Modulare Grundelement während der
zum
linearen Gebilde.
Das ebene Gebilde.
Im Zentrum des Sechsecks
die Knoten A und
H aufeinander
liegen
AnfangsStadium der
Faltung.
Man beachte, dass die
Punkte A und H jeweils
alternierend mit den
Ecken des Umrisses ver¬
bunden sind.
IV-40
Betrachten wir das Modell in einem Zwischenstadium des
Faltvorgangs:
Zwischenstadium der
Entfaltung
f.
Nehmen wir die
geschlossene Stabkette AGBCA, gebildet
durch die Stäbe AG, GB, BC
und CA,und ersetzen die Stäbe durch Vektoren, deren Modul mit der
der deren
Richtung
mit der
Länge und
Richtung des jeweils entsprechenden Stabes
einstimmt:
A
über¬
IV-41
So
erhalten wir:
AG
+
GB
+
BC
+
weil die Vektorenketten
CA
=
0,
geschlossen
ist.
Dieses Gesetz bleibt während des ganzen
Reihenfolge,
Faltvorgangs erhalten,
da sich die
in der die Stäbe durch Gelenke miteinander verbunden
sind, nicht
ändert.
Die Faltbarkeit des Gebildes
einer Achse senkrecht
Stablängen
zur
bringt
Ebene
TT
zu
mit
sich, dass alle Stäbe parallel
liegen
kommen. Das
bedingt, dass
zu
in einem bestimmten Verhältnis zueinander stehen.
die
Endstadium der
Entfaltung
Z
G
IV-42
Im
gefalteten Zustand müssen alle Vektoren auf die gleiche Linie
liegen
zu
kommen.
In diesem Teil ist die Summe:
AG
Es
+
GB + BC + CA
0
=
ergibt sich:
i -*¦ i
|ag|
i -*¦ i
-
|gb|
+
r->-*
|bc]
-> i
|ca|
i
-
=0
D.h.: Damit die Stabkette
gefaltet werden kann,
der alternierenden Stäbe jeweils gleich sein.
Diese
AG-GB
ii
äg-gF+fe"-ea"=o
III
AE
iv
hb"-bg
v
hf-f¥+ed"-dh~=o
vi
h7o-dc
Gleichungen
sechseckigen
Die
zuvor
ED + DC
-
+
+
die Summe der
Längen
BC-CA~=0
I
+
muss
-
CA
=
0
gf"-fh"=o
cb"-bh"=o
sind die
allgemeinen Bedingungen für die Faltbarkeit des
Modularen Grundelementes.
definierte
geometrische Bedingung der Faltbarkeit für die ele¬
mentarste Stabkette des Gebildes können wir auch wie
folgt
ausdrücken:
Für
jede beliebige geschlossene Stabkette, die noch aus der Struktur her¬
ausgelöst werden kann, gilt, dass die Summe der alternierenden Stablängen
jeweils gleich ist.
Dies kann durch die lineare Kombination der sechs oben
Gleichungen
bewiesen werden:
aufgestellten
IV-43
Gegeben sei die geschlossene Stabkette AE, ED, DC, CB, BG,
Durch Addition der
Gleichungen
GA.
I und III erhalten wir:
Äc"-c¥+BG-GA"+Äi"-ED"+DC-CA~=0
oder:
AE
Das
-
ED + DC
-
CB + BG
-
GA
=
0
folgende Beispiel zeigt, wie diese Bedingungen in die Anwendung umge¬
setzt werden können.
Beispiel: Bildung eines ebenen Fachwerkes
aus
sechseckigen
Modularen Grund¬
elementen
Wir
gehen
G und der
aus von
einem
Seitenlänge
a,
irregulären Sechseck mit den Ecken B, C, D, E,
so
dass sein Umriss einem
gleichseitigen Dreieck
Seitenlänge 2a entspricht. In diesem Fall sind
a'2/*/3~, die Radien AC, AE hingegen a-l/ZT.
mit den Ecken C, E, G und der
die Radien HB, HD und HF
=
F und
=
IV-44
•>
Tc
Ersetzen wir die Kanten durch
Stäbe, die in den Ecken durch Knoten gelenkig
miteinander verbunden sind.
Dabei wird der
Mittelpunkt
in zwei Knoten A und H
aufgeteilt, die alternierend
durch die Stäbe AC, AE, AG bzw. HB, HD, HF mit den Knoten des Umrisses
bunden sind.
Für diesen Fall
überprüfen
wir die vorher ermittelten
Faltbarkeit des Sechseckes. Aus
Gleichungen
Bedingungen für die
die Anzahl
unabhängiger
auf zwei reduziert:
AC
IV
Die
Symmetriegründen wird
Bedingungen
-
CB + BG
HB-BG +
-
GA
=
0
->-
GF-FH"=0->-
sind erfüllt.
—
/3
1
—
/3
ver¬
a + a
a-a + a
-
-^—
=
/3
—
/3
0
a
=
0
IV-45
r
^i
y
V
>
Die kinematischen
zu
den
zuvor
Eigenschaften (Freiheitsgrade) des Gebildes sind analog
beschriebenen kinematischen
Eigenschaften
des
sechseckigen
Ele¬
mentes.
Durch Aneinanderreihen einzelner Elemente in einem
wir ebene faltbare Fachwerke bilden.
dreieckigen
Rasten können
IV-46
UEBERTRAGUNG DES PRINZIPS DER
MITTELT
FALTBARKEIT, DAS MIT HILFE DES WUERFELS ER¬
WURDE, AUF ANDERE FALTBARE STRUKTUREN
Allgemeines
jetzt haben wir räumliche faltbare Modulare Grundelemente untersucht,
deren Projektion auf die Ebene TT während des Faltvorganges ein reguläres
Bis
Sechseck bildet.
Nun betrachten wir das
vom
Würfel
abgeleitete Modulare Grundelement in der
Position, in der sämtliche Ecken des ursprünglichen Würfels in der Ebene TT
liegen, so dass ihr Umriss ein reguläres Sechseck mit der Seite a und dem
Zentrum A und H bildet. (Dabei sind A und H die ursprünglichen Endpunkte der
Raumdiagonalen
Wir stellen
1. Der
des
Ausgangswürfels.)
folgendes
fest:
ursprüngliche Würfel hat sich in ein reguläres Sechseck mit seinen
Radien verwandelt.
2. Der
Mittelpunkt wird von den übereinanderliegenden Knoten A und H so ge¬
bildet, dass A und H jeweils alternierend durch Radialstäbe mit den Ecken
des
Polygons
Diese beiden
Faltbarkeit
verbunden sind.
Feststellungen ermöglichen die Uebertragung
auf andere polygonale Gebilde wie folgt:
des
Prinzips
der
IV-47
Uebertragung
des
Prinzips
Betrachten wir ein
der Faltbarkeit auf das
Quadrat
ABCD und seine
Ersetzen wir die Seiten und die
bzw. im
Mittelpunkt gelenkig
Als ebener Mechanismus
n
=
9
=
2g
=
F
=
2-5-8-3
=
-1
F
n
-
Halbdiagonalen.
Halbdiagonalen
durch
Stäbe, die in den Ecken
miteinander verbunden sind.
betrachtet, hat das Gebilde folgenden Freiheitsgrad:
5
F
-
Quadrat und seine Diagonalen
Das Gebilde hat einen
überzähligen
Stab.
Unterteilen wir den mittleren Knoten in zwei Knoten A und F, so dass A durch
die radialen Stäbe AC und AE mit den Knoten C und E, und F durch die Stäbe FB
und FD mit den Knoten B und D verbunden ist.
Das Gebilde erhält ein
neues
kinematisches Schema:
IV-48
Als räumlicher Mechanismus
n
=
8
g
=
6
F
=
3g
F
=3*6 -8-6=4
n
-
-
fort: Der
recht
A';
zur
C und
es
folgenden Freiheitsgrad:
6
Das Gebilde hat im Raum 4
Aus dieser
betrachtet, hat
Lage
Freiheitsgrade.
setzt sich der
Faltvorgang analog demjenigen des Sechseckes
Knoten F entfernt sich von der Ebene TT entlang einer Achse senk¬
Ebene TT, B und D bewegen sich auf der Ebene TT in der Richtung von
E entfernen sich von TT in der gleichen Richtung wie F.
(Siehe Abbildung auf nächster Seite.)
IV-49
*
~*C
*
X
>
Im
folgenden
untersuchen wir die
geometrischen Bedingungen, die erfüllt wer¬
den müssen, damit das Gebilde gefaltet werden kann, d.h. damit alle Stäbe
auf eine Linie
zu
liegen
vier Stabketten bilden:
kommen.
Analog
AC, CB, BE, EA;
zum
Fall des Sechseckes können wir
AE, ED, DC, CA;
FB, BE, ED, DF;
FD, DC, CB, BF.
O
O
O
o
IV-50
ergeben sich für die Faltung folgende geometrische Bedingungen, die
allgemein gültig sind für faltbare quadratische Gebilde mit ihren Diagonalen:
Daraus
0
ca
=
0
ii
ae
iii
fb-be
+
ex7-df"=o
iv
fd
+
cb
-
-
+
be
=
ac
-
cb
ea
i
ed + dc
dc
-
~
-
bf
=
0
Die
folgende Photosequenz zeigt das quadratische Grundelement während des
Faltvorgangs am Modell in Auf- und Seitensicht:
Bild 1:
Sämtliche Knoten liegen
auf der Referenzebene TT
und bilden ein Quadrat
mit seinen Diagonalen
Bild 2:
Zwischenstadium der
Faltung
IV-51
Bild 3:
Endstadium der
Faltung.
Sämtliche Stäbe des
Grundelementes sind um
eine Achse gruppiert
Uebertragung
des
Prinzips der Faltbarkeit auf
das Achteck und seine Radien
Betrachten wir ein Achteck und seine Radien. Wir ersetzen die Seiten und
Radien durch Stäbe, die in den Ecken bzw. im
Mittelpunkt
der
Figur gelenkig
miteinander verbunden sind.
Als ebener Mechanismus hat das Gebilde
F
=
2g
F
=
2-9
F
=
Das
n
-
-
-
16
folgenden Freiheitsgrad:
3
-
3
-1
Gebilde ist stabil und hat einen
überzähligen Stab.
IV-52
Unterteilen wir den mittleren Knoten in zwei Knoten A und I,
so
dass A mit
den Knoten C, E, G, I und I mit den Knoten B, D, F, H durch radiale Stäbe
verbunden ist.
Als räumlicher Mechanismus hat
n
=
folgenden Freiheitsgrad:
16
=
8
F
=
3g
F
=3*10 -16 -6=8
g
es
-
n
-
6
Das Gebilde hat im Raum 8
Freiheitsgrade.
Damit das Gebilde
gefaltet werden kann, müssen die geometrischen Bedingungen
der Faltbarkeit für jede einzelne Stabkette erfüllt werden. In diesem Fall
können wir acht Stabketten bilden:
AC, CD, DE, EA;
AE, EF, FG, GA;
AG, GH, HI, JA;
AI, IB, BC, CA;
JB, BC, CD, DJ;
JD, DE, EF, FJ;
JF, FG, GH, HJ;
JH, HI, IB, BJ.
IV-53
Daraus
ergeben sich für die Faltung folgende geometrische Bedingungen, die
allgemein gültig
sind für faltbare
ac
ii
af-ih +
iii
äg-gF+fe"-eä"=o
iv
ä¥-ed"+dc"-cä"=o
v
5i"-BT+i¥-Hj=o
VI
j¥-HG
vii
jF-fe"+ed"-dj
o
viii
jd"-dc"+c¥-bj
o
+
-
ia
0
i
-
cb + bf
achteckige
=
hg~-gä~=0
GFr-FJ*=0
=
=
Gebilde mit ihren
Diagonalen:
IV-54
Die
mit
folgende Photosequenz zeigt die Faltung eines Modularen Grundelementes
achteckiger Projektion auf die Referenzebene TT in Auf- und Seitensicht:
Bild 1:
Das entfaltete Modell.
Sämtliche Knoten des
Modells befinden sich
auf der Referenzebene TT
und bilden ein reguläres
Achteck
Bild 2:
Zwischenstadium der
Faltung
Bild 3:
Endstadium der Faltung.
Sämtliche Segmente des
Grundelementes befinden
sich auf einer Strecke
IV-55
Modulares Bauprinzip
Aufgrund der beschriebenen Prinzipien der Faltbarkeit für das Quadrat und
seine Diagonalen sowie für das Achteck und seine Radien kann man die einzelnen
Elemente in einem quadratischen bzw. achteckigen Raster so anordnen, dass
ebene faltbare Strukturen entstehen.
a) Quadratisches Netz
Als Varianten des
trapezoidale
quadratischen
Netze:
b) Netz
aus
Quadraten und Achtecken
Netzes betrachten wir auch rhombische und
V
Die Faltung sphärischer Fachwerke
V-l
Die Faltung sphärischer Fachwerke
EINFUEHRUNG
Im
vorangehenden Kapitel
haben wir
uns
Beschreibung von Faltbarkeitsräumlichen planparallelen Fach¬
mit der
Prinzipien, die zur Erzeugung von ebenen oder
werken gebraucht werden können, befasst.
Die derart
erzeugten faltbaren Fachwerktypen können miteinander oder mit
deren nicht fatlbaren Elementen
so
an¬
werden, dass ein raumabgrenzen¬
kombiniert
des Gebilde entsteht.
Um räumliche
nichtplanparallele Fachwerke
zu
erzeugen, können wir
von
geo¬
metrischen Gebilden wie
Zylinder, Sphäre, Paraboloid, hyperboloidisches
Paraboloid usw. ausgehen, indem wir an die gegebene Fläche ein aus Stäben
und Knoten bestehendes Gebilde assoziieren, so dass die Knoten auf die räum¬
liche Fläche
zu
liegen
kommen.
Fachwerke, die eine räumliche Fläche beschreiben, übernehmen als
grenzende Gebilde die Eigenschaften der erzeugenden Fläche.
Wichtige Aspekte
Raum ab¬
der
nichtplanparallelen räumlichen Fachwerke sind diejeni¬
gen, die sich vom geometrischen Charakter des Gebildes ableiten lassen, zum
Beispiel doppeltgekrümmte Flächen (z.B. Sphäre) ergeben Fachwerke mit einer
besseren
Tragfähigkeit und Gesamtstabilität als einfach gekrümmte Fachwerke
(z.B. Zylinder). Hingegen lassen sich einfach gekrümmte Flächen einheitlicher
einteilen als
Knoten
doppelt gekrümmte, d.h. die Länge der Stäbe und die Art der
weisen kleinere Unterschiede auf als im Fall der doppelt gekrümmten
Fachwerke.
folgenden Abschnitt wird aus allen möglichen
herausgegriffen und die Fachwerke studiert, die
Im
räumlichen Flächen die
Sphäre
sich in diese einschreiben
lassen.
Gründe dafür sind:
-
Die
Sphäre ist
nis zwischen
von
den räumlichen Flächen
diejenige,
bei der das Verhält¬
eingeschlossenem Volumen und einschliessender Fläche
am
grössten
ist.
-
Die bei
sphärischen Fachwerken gewonnenen Erkenntnisse bezüglich geometrischer
Einteilung und Faltprinzipien
werkgebilde übertragen.
lassen sich leicht auf andere räumliche Fach¬
V-2
Von allen
nichtplanparallelen
Sphäre verwendet.
räumlichen Fachwerken wird
vor
allem die
V-3
Die Montagekuppel als Beispiel für sphärisches Fachwerk
Türkgü definiert diesen Begriff in seiner Arbeit "Beitrag
der Montagekugelkuppeln mit Berücksichtigung von konstruktiven
(Diss. TU Berlin, 1973, S. 6-7) wie folgt:
H.C.
zur
Geometrie
Kriterien"
Der Ausdruck 'Montagekugelkuppel' (kurz Montagekuppel)
bezeichnet eine aufgelöste Kuppelbauweise, deren Konstruk¬
tionsglieder vor allem unter Berücksichtigung der jeweili¬
gen Transport- und Montageanforderungen dimensioniert
werden. Durch die Auflösung der Kugelfläche in tragende
Konstruktionsglieder wird eine Vorfertigung möglich. Die
Tragglieder (Knoten, Stäbe) liegen auf einer bzw. zwei
konzentrischen Kugeloberflächen. Die Felder zwischen den
Stäben werden mit Platten bedeckt, die auch in die Trag¬
wirkung einbezogen werden können. Ist die Dachhaut aus
einem biegsamen Material, so wird diese an die Knoten
"
aufgehängt
Es besteht die
...
a
b
c
Möglichkeit, die Montagekuppel
aus
Stäben
-
gekrümmten bzw. gefalteten Flächenelementen
Kombinationen von (a) und (b)
-
-
zusammenzusetzen.
Folgende Anforderungen werden
stellt:
a
an
die
Montagekuppeln ge¬
herstellungstechnisch
-
identische Stäbe oder geringe Anzahl von Stabtypen
identische Knoten oder geringe Anzahl von Knoten
identische Flächenanteile oder geringe Anzahl von
Flächentypen
b
-
c
-
transporttechnisch
geringes Gewicht
raumsparende Stapelung
transportierbare Elementgrössen
montagetechnisch
eine unkomplizierte, witterungsunempfindliche Montage.
Da die Montagekuppeln meistens aus kleinen Stäben,
dünnen Metall- und Kunststoffplatten ausgebildet wer¬
den, sind die Transportabmessungen für die Gestaltung
und
Dimensionierung
der Elemente entscheidend."
folgenden Abschnittes ist, unter Berücksichtigung der obgeAnforderungen geometrische Prinzipien herauszukristallisieren, die
Das Ziel des
nannten
es
uns
erlauben, faltbare sphärische Fachwerke
zu
bilden.
V-4
Unter FALTUNG verstehen wir einen
Vorgang, in dem durch die Auflösung aus¬
gewählter Bindungen der Struktur relative Bewegungen der Teile zugelassen
werden, bei denen alle Stäbe um eine Achse gruppiert zu liegen kommen.
Faltbarkeit kann für eine Struktur in verschiedener Hinsicht
von
Vorteil
sein:
a)__Herstellung
Ein grosser Teil der
Arbeiten, die
man
bei konventioneller
Montage
am
Bau¬
platz verrichtet, können schon im Werk ausgeführt werden.
b) Transport
Die
Kuppel lässt sich in gefaltetem Zustand leicht transportieren.
c)__Montage
Die
Kuppel kann infolge der Vorbereitungen im Werk und infolge des falt¬
baren Charakters des Gebildes innert kürzester Zeit und mit
aufgestellt werden.
wichtige Aspekte
Zwei
müssen
bezüglich
der
Bildung
wenig Aufwand
faltbarer Stabnetzwerk¬
kuppeln untersucht werden:
-
Die
Geometrie, die eine Unterteilung der Kuppel in Flächen erlaubt,
d.h. die
Erzeugung
von
Polyedern, die als räumliches
bei einer minimalen Anzahl
von
Stabtypen
die
Netz
dienen, und die
jeweiligen Anforderungen
er¬
füllen.
-
Die faltbaren
Grundelemente, die im räumlichen Netz des Polyeders ange¬
ordnet werden sollen, so dass ihre gemeinsame Faltung eine Faltung des
ganzen Gebildes
Deß ersten
zur
Folge hat.
Aspekt, die Geometrie sphärischer Fachwerke, werden wir
streifen, da wir
nur
diejenigen
Fälle
hier
nur
untersuchen, die später als Beispiele
zusammenfaltbarer Strukturen behandelt werden. Im
Thema auf die Arbeit von H.C. Türkgü verwiesen.
übrigen
sei
zu
diesem
kurz
V-5
In diesem Abschnitt befassen wir
uns
mit dem zweiten
Aspekt, der
Unter¬
Grundelementen, die sich durch die Uebertragung des
Prinzips der Faltbarkeit des Würfels, das im vorangehenden Abschnitt unter¬
sucht wurde, ergeben. So definieren wir hier Elemente, die aufgrund ähnlicher
Prinzipien faltbar sind, erläutern ihre geometrischen und kinematischen Eigen¬
schaften und belegen durch Beispiele Möglichkeiten der Anwendung.
suchung
von
faltbaren
V-6
ZUR GEOMETRIE SPHAERISCHER FACHWERKE
allgemein definiert ist ein Polyeder ein räumliches Gebilde, das durch
die Abgrenzung eines Volumens mittels Ebenen entsteht, die sich zur Bildung
von Flächen, Kanten und Ecken schneiden.
Ganz
Ein
Polyeder kann konvex oder konkav sein.
Polyeder sei dann konvex, wenn sich, von der Ebene einer beliebigen
Fläche des Polyeders aus gesehen, der ganze Körper auf der gleichen Seite
Ein
der Ebene befindet.
Das Verhältnis zwischen der Anzahl der Flächen
Ecken E wird durch die Eulersche Formel
F
-
K + E
=
2.
F, der Kanten K und der
festgelegt:
*)
Flächen, Kanten und Ecken sind die wichtigsten Elemente des Polyeders;
durch ihre Anzahl und die Art ihrer
Anordnung können wir die verschiedenen
Polyeder kennzeichnen.
*)
aus:
Introduction and Analogy in Mathematics von G. Polya, Vol. I, S.
Princeton University Press, Princeton, New Jersey, 1954.
37,
V-7
DIE FUENF PLATONISCHEN KOERPER
(auch regelmässige Polyeder genannt)
Das Tetraeder
Anzahl Flächen F:
4; gleichseitige Dreiecke, 4 F.,
Anzahl Kanten
K: 6
Anzahl Ecken
E: 4
Durchmesser der umschriebenen
des
Sphäre:
D
=
1.22474 a, wobei
a
die
Kantenlänge
Polyeders ist.
*) Schlafli-Code kF. (aus der Kristallographie):
k
Art der Fläche, d.h. die
Polyeders, Index i
Anzahl Ecken jeder einzelnen Fläche; somit steht 3 für Dreieck und
4 für Viereck, usw.
=
Anzahl Flächen eines
=
V-8
Der Kubus
6F4
K
:
12
E
:
8
D
:
1.73205
a
Das Oktaeder
8 F
K
:
12
E
:
6
D
=
1.41421
a
V-9
Das
Pentagondodekaeder
12 F
5
K
30
E
20
D
2.80252
a
Das Ikosaeder
20
F3
K
:
30
E
:
12
D
:
1.90211
a
V-10
HALBREGELMAESSIGE POLYEDER
Abstumpfung regulärer Polyeder
Die
als Mittel
zur
Bildung halbregelmässiger
Polyeder:
jeder Ecke
Polyeders wird durch eine Ebene senkrecht zur Verbindungs¬
achse zwischen der Ecke und dem Mittelpunkt des Polyeders eine Pyramide ab¬
geschnitten, so dass die Kante des ursprünglichen Polyeders in drei Teile
In
des
zerfällt.
Auf diese Weise erhalten wir
Das
folgende halbregelmässige Polyeder:
abgestumpfte Tetraeder
/
/
/
1\
/
/ \
\
4 F„
3
/
/
/,
<^
^
\L-
+
4 F,.
6
K
•
18
E
:
12
D
:
2.34521
a
V-ll
Der
abgestumpfte Kubus
--rf
¦i
r
6
F0
O
+
8 F_
O
K
:
36
E
:
24
D
:
3.55765
a
JL
k-
>i
X.
Das
abgestumpfte
Oktaeder
4\
// \ \
Z
A
/ /
8 F^
6
4~
tr-
f.
\\ //
wV//
/
r^
/
/
/
+
6 F.
4
K
:
36
E
:
24
D
:
3.16228
a
V-12
Das
abgestumpfte Pentagondodekaeder
c^i=
nr
K
F3
20
y
Y
+
F1Q
12
K
:
90
E
:
60
D
=
3.09317
a
v
Das
abgestumpfte
Ikosaeder
12 F
+
20 F
K
:
90
E
:
60
D
:
4.95604
a
V-13
TRIANGULIERTE POLYEDER
Das
Tetraeder, das Oktaeder und das Ikosaeder sind
aus
gleichseitigen Drei¬
zusammengesetzt; die übrigen regelmässigen Polyeder sowie diejenigen
halbregelmässigen Polyeder, die durch Abstumpfung der regelmässigen gebil¬
det werden, bestehen nicht nur aus Dreiecken, sondern teilweise oder sogar
ecken
ausschliesslich
-
-
-
-
aus
anderen
Polygonalformen:
Quadraten
Fünfecken,
Sechsecken
usw.
derjenigen ausgewählten Fälle, die später
als Beispiele von faltbaren Polyedern verwendet werden, mit welcher Methode
triangulierte Polyeder aufgrund bestehender, nicht triangulierter, regel¬
mässiger oder halbregelmässiger Polyeder gebildet werden.
Im
folgenden zeigen
Bei der einfachen
wir anhand
Triangulation
Polyeders werden die Flächenmittel¬
punkte auf die umhüllende Sphäre zentral projiziert, und die projizierten
Punkte mit den Ecken der
eines
jeweiligen
Fläche des
Ausgangspolyeders
verbunden.
V-14
doppelten Triangulation wird zusätzlich der Mittelpunkt jeder Kante
des Ausgangspolyeders auf die umhüllende Sphäre projiziert. Anschliessend
verbindet man den projizierten Punkt einerseits mit den Ecken an den Enden
seiner zugehörigen Kante und andererseits mit den auf die Sphäre projizier¬
ten Mittelpunkten der beiden Flächen des Ausgangspolyeders, die an die Kante
Bei der
angrenzen.
r-O
beachten, dass die Triangulation eines Polyeders mit derjenigen
Es ist
zu
seines
Dualpolyeders
Zwei
übereinstimmt.
Polyeder sind dual,
wenn
Polyeders
anderen und umgekehrt. So ist
die Anzahl der Ecken des einen
übereinstimmt mit der Anzahl der Flächen des
selber, der Kubus ist dual mit dem Oktaeder und
umgekehrt, das Pentagondodekaeder mit dem Ikosaeder und umgekehrt.
das Tetraeder dual mit sich
V-15
Triangulation
des Würfels
^i^f^E^eJTria^g^lation
24 F„
Kanten:
K
=
0.57735 D
K
=
0.45970 D
Anzahl:
¦
:
12
24
&
Ecken:
E
(4 Anschlüsse)^ :6
E
(6 Anschlüsse)':8
Doppelte Triangulation
48 F.,
Kanten:
K
=
0.45970 D
:
24
K
=
0.30291 D
:
24
K
=
0.38268 D
:
24
K,
Ecken:
E
(4 Anschlüsse):12
E
(6 Anschlüsse): 8
E
(8 Anschlüsse): 6
\
V-16
Triangulation des abgestumpften Oktaeders
Einfache
Triangulation
72 F.,
K
K2
K3
=
0.31623 D
:
36
=
0.22975 D
:
24
=
0.33571 D
:
48
Kl
E
(6 Anschlüsse):32
E„
(4 Anschlüsse): 6
Triangulation des Pentagondodekaeders
D2PJpelte_Triangulation
120 F_
K
K2
K3
=
0.32043 D
:
60
=
0.27327 D
:
60
=
0.18142 D
:
60
Kl
E
(10 Anschlüsse): 12
E
( 6 Anschlüsse): 20
E
( 4 Anschlüsse): 30
h
Ka
V-17
Triangulation des abgestumpften Ikosaeders
Einfache
Triangulation
180 F„
K
=
0.20177 D
:
90
K
=
0.17431 D
:
60
K
=
0.20621 D
:
120
E
(6 Anschlüsse): 60
E
(5 Anschlüsse): 12
E^
(3 Anschlüsse): 20
K3
Kl
-V
Doppelte Triangulation
360 F.,
K
=
0.10141 D
:
180
K
=
0.14325
D
:
60
K
=
0.17431 D
:
60
=
0.17541 D
:
120
=
0.20621 D
:
120
K4
Kc
E
(12 Anschlüsse): 20
E„
( 4 Anschlüsse): 90
E^. ( 6 Anschlüsse) : 60
E4
(10 Anschlüsse): 12
K5
V-18
Prinzipien der Faltbarkeit
von
sphärischen Fachwerken
DIE FALTBARKEIT PYRAMIDALER ELEMENTE
Allgemeines:
Die Gemeinsamkeit aller
Variationen, die
abgeleitet
Grundelementes des Würfels
von
der Faltbarkeit des Modularen
und im
vorangehenden Abschnitt defi¬
niert wurden, besteht darin, dass für jede Figur in einer bestimmten Phase
des Faltvorgangs sämtliche Eckpunkte in der Ebene TT liegen, wo sie ein
Viereck bzw. ein Sechseck bzw. ein Achteck
usw.
bilden.
folgenden Abschnitt werden wir die behandelten Prinzipien und Beziehungen
auf pyramidale Gebilde übertragen.
Im
PYRAMIDEN AUF SECHSECKIGER BASIS
Betrachten wir im
der
Länge b
der Ebene
TT
=
/a2
folgenden
+
h2,
eine
Pyramide mit der Höhe h und den Kanten mit
deren sechseckige Basis mit der Seitenlänge a in
liegt.
a
77
V-19
Ersetzen wir die Kanten durch
verbunden sind,
unterteilt
HB, HD,
so
Stäbe, die in den Ecken gelenkig miteinander
Spitze der Pyramide in
jeweils alternierend durch
dass die
wird, welche
HF mit den Basisknoten verbunden
die zwei Knoten A und H
die Stäbe AC, AE, AG bzw.
sind.
Spitze der Pyramide liegen,
zusammengefasst werden.
Die beiden Knoten A und H, die in der
auch
zu
einzigen
einem
Knoten
können
Betrachten wir das Gebilde als räumlichen Mechanismus und untersuchen wir
der kinematischen
Veränderung
die
Verhältnisse,
wenn
A und H entweder
a) verbunden, oder b) getrennt sind:
n
=
12
g
=
7
F
=
3 g
F
=
3*7
a)
-
-
-
-
n
12
6
-
-
6
=
3
6
=
6
12
-
12
-
Das Gebilde hat bei einer
Man
beachte die
Analogie
Trennung der Knoten A und H sechs Freiheitsgrade.
zum
Fall der Faltbarkeit des Würfels.
V-20
Geometrische Transformation beim
Faltvorgang des Gebildes
Durchschlag wird hier die geometrische Transformation verstanden, bei
ein Knoten des Gebildes die Ebene TT durchdringt und auf die andere
Unter
der
Seite
von TT
zu
liegen kommt.
Durchschlagsbedingungen:
Untersuchen wir während des
den Ecken
Faltvorgangs
das
geometrische
Verhältnis zwischen
sechseckigen Basis in der Ebene TT und der sich
entfernenden Knoten der Spitzen A und H. Betrachten wir denjenigen Fall, bei
dem sich A während des Faltvorgangs in Richtung der Höhe h (senkrecht zu TT)
von
des Umrisses der
H weg auf die Ebene TT
Knoten der
sechseckigen
zubewegt und diese durchdringt,
Basis in der Ebene
TT
währenddem alle
bleiben.
?.
^>
4
-4Ä
?».
-^
wird, bei welchem Längenverhältnis der Basisstäbe a zu den Radial¬
stäben b ein Durchdringen der Ebene TT mit dem Knoten A möglich ist. Be¬
trachten wir jenen Grenzfall, bei dem sich der Punkt A in der Ebene TT be¬
Gesucht
findet, und die Seitenpaare CD bzw. EF, FG bzw. GB, BC jeweils auf einer
liegen, so dass die ursprünglich sechseckige Basis der Pyramide
sich in ein gleichseitiges Dreieck mit den Eckpunkten C, E und G und der
Seitenlänge 2a verwandelt.
Strecke
V-21
t
?.
CT
/
*<&
tf
V
¦\
*C
So
ergibt sich für das Verhältnis
von
b
zu
a:
2
a
—
/T
und für das Verhältnis
a
Ausgehend
von
entfernt sich
Abstand h
—
von
h
zu a:
/ 3
seiner Position in der Ebene
von
TT
durchschlägt
dieser und erreicht eine bestimmte
(Höhe der ursprünglichen Pyramide) und
setzten Seite der Ebene TT ebenfalls der Abstand h
dass die Knoten der Basis wie bei ihrer
bilden.
A die Ebene TT,
H
Lage, in der A den
auf der entgegenge¬
von
dieser einnimmt,
Ausgangslage wieder ein Hexagon
so
V-22
n
er
*S
er
7
Von dieser Position
aus
setzt sich der
Faltvorgang analog
zur
Faltung des
Würfels fort, d.h. die Ecken C, E und G, die durch die Kanten b mit A
bunden
sind, entfernen sich entgegengesetzt
in der Ebene
TT
liegenden Eckpunkte B,
D und
zu
A
mide
um
so
der Ebene TT, und die
F, die durch b mit H verbunden
sind, bewegen sich radial auf das ursprüngliche
mide zu,
von
Zentrum der Basis der
dass für den Endzustand sämtliche Stäbe der
eine Achse
gruppiert sind.
^>
ö
•*z>
^
ver¬
ö
p>
TI
Pyra¬
ursprünglichen Pyra¬
V-23
Analog
Fall des Würfels
zum
gelten
hier dieselben
Gleichungen als notwendige
für die Faltbarkeit der einzelnen Stabketten des Gebildes.
Bedingungen
Pyramide mit regulärer sechseckiger Basis können wir aus Gründen
Symmetrie die sechs Gleichungen in eine einzige zusammenfassen:
Im Fall der
der
b-a
PYRAMIDEN AUF
+
a-b
QUADRATISCHER
0
=
BASIS
Analog zur Pyramide mit sechseckiger Basis untersuchen wir nun die Pyramide
mit quadratischer Basis, mit der Basisseitenlänge a, der Höhe h und der Kan¬
tenlänge
b.
•
fl
•o
*
-^
Wir ersetzen die Kanten wieder durch Stäbe, die in den Knoten
nander verbunden
hängige
gelenkig
mitei¬
sind, und bilden die Spitze durch zwei voneinander unab¬
Knoten A und F, die wir alternierend durch die Stäbe AC und AE bzw.
FB und FD mit den Basisstäben verbinden.
Betrachten wir das Gebilde als räumlichen Mechanismus. Je nachdem, ob A und
F entweder
a) miteinander verbunden, oder b) voneinander unabhänig sind,
V-24
verändert sich der
a)
n
g
b)
=
8
=
5
Freiheitsgrad des Gebildes wie folgt:
F=
3g-n-6
F=
15 -8-6=1
n
=
8
=
6
g
F
=
18 -8-6
Bei einer
=
4
Trennung der
Knoten A und F hat das Gebilde 4
Geometrische Transformation beim
Freiheitsgrade.
Faltvorgang des Gebildes
Durchschlagsbedingungen:Pyramide mit sechseckiger Basis untersuchen wir während des Falt¬
vorgangs das geometrische Verhältnis zwischen den Ecken des Umrisses der
quadratischen Basis in der Ebene TT und den sich voneinander entfernenden
Knoten der Spitze A und F:
Analog
zur
Wir wählen für
unsere
Faltvorgangs
von
A
Betrachtung denjenigen Fall,
F weg auf die Ebene TT
während alle Knoten der
zubewegt und diese durchschlägt,
quadratischen Basis
in der Ebene TT bleiben.
E/
?
-Q
fr
¦V
*>
/C
\>
für den sich während des
V-25
Grenzfall, bei dem sich
Nehmen wir den
BE bzw.
Stabpaare CB,
CD, DE jeweils auf eine Strecke
alle vier Knoten sich auf einer Strecke mit der
So
ergibt sich
für das Verhältnis
b
von
befindet, und die
A in der Ebene TT
zu
liegen kommen,
zu
d.h.
Länge 2a befinden.
a:
*<1
a
—
und für das Verhältnis
*
von
entfernt sich
h
zu
a:
<
a
Ausgehend
von
/ 2
—
seiner Position in der Ebene TT
durchschlägt
A die Ebene TT,
dieser und erreicht eine bestimmte Lage, in der A den Ab¬
von
stand h (Höhe der
ursprünglichen Pyramide) und
Seite der Ebene
ebenfalls den Abstand h
TT
Knoten der Basis wie bei ihrer
von
H auf der
entgegengesetzten
dieser einnimmt, so dass die
Ausgangslage wiederum ein Quadrat bilden.
tF
¦#-'
•«a
+A
Von dieser Position
Quadrates
aus
mit seinen
Stäbe des Gebildes
setzt sich der
um
Halbdiagonalen
eine Achse
bis
Faltvorgang analog
zum
zu
demjenigen
des
Endzustand fort, bei dem sämtliche
gruppiert sind.
V-26
yf-^
Analog
zu
dingungen
jenem Fall gelten hier dieselben Gleichungen als notwendige
Be¬
für die Faltbarkeit der einzelnen Stabketten des Gebildes.
Im Fall der
Pyramide mit regulärer quadratischer Basis können wir aus Sym¬
metriegründen die vier Gleichungen in eine einzige zusammenfassen:
b
-
a
+ a
-
b
V-27
PYRAMIDEN MIT ACHTECKIGER BASIS
Betrachten wir eine
länge
a, der Höhe h
Pyramide mit der regulären achteckigen Basis der Seiten¬
und der Kantenlänge b.
*&
^
vorangehenden Fällen ersetzen wir die Kanten durch Stäbe, die
in den Ecken gelenkig miteinander verbunden sind, und unterteilen die Spitze
der Pyramide in die zwei Knoten A und J, die mit den Basisknoten alternierend
Analog
den
zu
durch die Stäbe AC, AE, AG, AI bzw. JB, JD, JF, JH verbunden sind.
Betrachten wir das Gebilde als räumlichen Mechanismus. Je nachdem, ob die
Knoten A und J entweder
a) miteinander verbunden oder b) voneinander unab¬
hängig sind, verändert sich der Freiheitsgrad des Gebildes wie folgt:
a)
=
16
=
9
F
=
3 g
F
=
3-9
n
=
16
g
=
10
n
g
b)
--
--
n
16
F=3-10-16-6=8
Wenn
grade
man
.
die Knoten A und J voneinander trennt,
so
hat das Gebilde 8 Freiheits¬
V-28
Geometrische Transformation beim
Faltvorgang des Gebildes
Durchschlagsbedingungen:
Analog zu den vorher beschriebenen Pyramiden untersuchen wir während des
Faltvorgangs das geometrische Verhältnis zwischen den Ecken des Umrisses
der achteckigen Basis in der Ebene TT und den sich voneinander entfernenden
Knoten der Spitze A und J. Wir wählen für unsere Betrachtungen denjenigen
Fall, bei dem sich während des Faltvorgangs A von J weg auf die Ebene TT zu¬
bewegt und diese durchschlägt, während alle Knoten der achteckigen Basis
in der Ebene
TT
bleiben.
t
jr
^
er
K
*
17
Nehmen wir den Grenzfall, bei dem sich A in der Ebene
TT
befindet, und die
Stabpaare der Basis CD, DE bzw. EF, FG bzw. GH, HI bzw. IB, BC jeweils auf
eine Strecke zu liegen kommen, so dass sich die ursprünglich achteckige Basis
der Pyramide in ein Quadrat mit den Ecken C, E, G, I und der Seitenlänge 2a
verwandelt.
So
ergibt sich für das Verhältnis
a
—
TT
und für das Verhältnis
von
-i5l<
a"
TT
h
zu
a:
von
b
zu a:
V-29
Ausgehend
von
entfernt sich
stand h
seiner Position in der Ebene
von
TT
ebenfalls den Abstand h
setzt sich
von
Ausgangslage
Knoten der Basis wie in ihrer
Faltvorgang
A die Ebene TT,
dieser und erreicht eine bestimmte Lage in der A den Ab¬
J auf der
(Höhe der ursprünglichen Pyramide) und
Seite der Ebene
Der
durchschlägt
TT
analog
nun
zu
dieser einnimmt,
so
dass die
ein Achteck bilden.
demjenigen des Achteckes in der
Endlage sämtliche Stäbe
Ebene fort, bis in der
entgegengesetzten
des Gebildes
um
eine Achse
gruppiert sind.
Analog zu jenem Fall gelten hier dieselben Gleichungen als notwendige
dingungen für die Faltbarkeit der einzelnen Stabketten des Gebildes.
Pyramide mit regulärer achteckiger Basis können wir die
Gleichungen aus Symmetriegründen in einer einzigen zusammenfassen:
Im Fall der
b-a
+
a-b
=
Be¬
acht
0
Bemerkung:
Prinzipien der Faltung pyramidaler Elemente mit vier¬
eckiger bzw. sechseckiger bzw. achteckiger Basis können auf weitere pyrami¬
dale Elemente, die eine Basis mit einer noch grösseren Anzahl Ecken haben,
übertragen werden. Dabei muss die Basis der pyramidalen Elemente aber immer
Die hier definierten
gerade Anzahl Stäbe aufweisen, damit bei einer Trennung der zwei in der
Spitze liegenden Knoten viergliedrige Stabketten gebildet werden können.
Geht man nämlich von einem pyramidalen Element mit einer ungeraden Anzahl
Stäbe in der Basis aus, so wird bei einer Trennung der Spitze in zwei Knoten
eine
mindestens eine der daraus resultierenden Stabketten
bedeutet, dass sie unverzerrbar (F
nach nicht mehr falten lässt.
=
dreigliedrig;
dies aber
0) ist, und dass das Gebilde sich dem¬
V-30
Anwendung der vorher definierten Prinzipien
licher Strukturen
zur
Faltung
räum¬
ALLGEMEINES
Alle bisher beschriebenen
wendung
Faltung
in der
krümmte Flächen
pyramidalen Modularen Grundelemente finden ihre
An¬
Strukturen, denen einfach oder doppelt ge¬
räumlicher
z.B. die
eingeschrieben sind,
Sphäre.
r^.
V^\
Abbildung zeigt,
Wie die
Schnitt mit der Ebene
TT
entstehen auf der
ein Kreis mit dem Radius
Höhe h, in welche sich z.B. eine
Seitenlänge
a
=
r
Sphäre mit Radius
Pyramide
mit
r
sechseckiger
durch
Pyramide
Spitze der Pyramide in zwei
F, die mit den Knoten der Basis alternierend durch Stäbe
bunden sind. Es handelt sich somit
so
Basis mit der
Stäbe, die in den Ecken gelenkig
miteinander verbunden sind, und unterteilen die
das
und eine Kalotte mit der
und der Höhe h einschreiben lässt.
Ersetzen wir die Kanten der
Knoten A und
R durch den
gefaltet
werden kann, wie
es
sechseckiger Basis" gezeigt wurde.
um
sphärisches Fachwerk,
"Pyramide mit regulärer
ein elementares
im Abschnitt
ver¬
V-31
Vorgehen:
Indem wir
wir im
von
einfachen
zu
folgenden Abschnitt
komplexeren Gebilden vordringen, zeigen
anhand von Beispielen wie sich die Pyramidalen
immer
Grundelemente, die im vorangehenden Abschnitt als faltbar definiert wurden,
in
sphärische
Netze einordnen lassen und diese
faltbaren Fachwerken machen
zu
können.
Unter Faltbarkeit verstehen wir wie bei früheren
bilde durch selektive
und
Auflösung
von
Fällen, dass bei einem Ge¬
Bindungen relative gegenseitige Drehungen
Verschiebungen der einzelnen Teile der Struktur möglich werden,
alle Stäbe
Für die
um
eine Achse
so
dass
gruppiert werden können.
geometrischen Grund¬
Montagekuppel" geschaffen wurden.
Bildung der Beispiele stützen wir
lagen, die im Abschnitt "Geometrie der
uns
auf die
V-32
DAS EINFACH TRIANGULIERTE, ABGESTUMPFTE OKTAEDER ALS RAEUMLICHES NETZ ZUR
BILDUNG FALTBARER FACHWERKE
/
beachten, dass die Flächen des ursprünglichen abgestumpften Oktaeders
Man
beim
triangulierten abgestumpften Oktaeder
Pyramiden
Basen von
Beispiel
aus
sechseckigen bzw. achteckigen
werden.
1:
Betrachten wir einen Teil des
sei
zu
vier
Pyramiden
ratischer Basis
auf
gebildet:
triangulierten abgestumpften
sechseckiger Basis und
aus
Oktaeders. Dieser
einer
Pyramide
mit
quad¬
V-33
Ersetzen wir die Kanten durch
Stäbe, die in den Ecken gelenkig miteinander
verbunden
sind,
faltbaren
pyramidalen Elementen
so
dass ein räumliches Fachwerk entsteht, das sich
=
n
=
0.31623 D
:
20
n
=
0.22975
D
:
4
n
=
0.33571
D
:
24
Es ist
zu
48
beachten, dass der Faltvorgang dadurch zustande kommt, dass die
Spitze jedes
bildet
SS
Eigenschaften des Gebildes
(-Anzahl Stäbe)
n
fünf
zusammensetzt.
1
Geometrische
aus
einzelnen
wird, d.h. in
pyramidalen
unserem
Elementes durch zwei
getrennte Knoten ge¬
Fall, bei dem wir fünf Modulare Grundelemente
haben, erhalten wir bei entfaltetem Zustand fünf Doppelknoten:
(Anzahl Knoten bei eintfaltetem Zustand) g
=
21
(Anzahl Knoten während des Faltvorgangs) g
=
26
Betrachten wir das Gebilde als räumlichen Mechanismus:
Der
Freiheitsgrad
verändert sich
je nachdem,
jedes Elementes a) miteinander verbunden,
a)
48
n
=
g
=
F
=3g-n-6=9
21
ob die beiden Knoten
oder
an
der
Spitze
b) voneinander getrennt sind.
V-34
b)
n
g
F
Will
=
48
=
26
=
3g
-
n
6
=
24
das Gebilde in entfaltetem Zustand in ein starres
man
indem die
Basispunkte durch Bindungen
stellen) festgehalten werden,
Bei
Will
mindestens 9
man
52
=
21
F
=
3g
F
=
5
g
15
=
Bindungen.
jeder
wirtschaftlichen und konstruktiven Gründen die Anzahl
auf das Minimum
beschränken,
so
kann
durch Einführen
man
nötiger
von
vier
Kuppel den Mechanismus wie
beeinflussen:
=
n
6
konstruktiven Gründen
aus
zusätzlichen Stäben beim entfalteten Zustand der
folgt
+
Auflagerpunkte drei Bindungen erhalten.
man aus
Auflager
benötigt
(Fundament oder Verankerungs¬
Grund
Beispiel wird aber im allgemeinen
unserem
der acht
so
zum
System umwandeln
-
n
-
6
So wird die Anzahl der erforderlichen äusseren
Bindungen 5
genügen vier Auflagerstellen mit dreifacher Bindung,
faltetem Zustand stabil
zu
machen und
es
am
um
+
6
=
11, und
es
das Gebilde in ent¬
Grund festzuhalten.
V-35
Durchschlagsbedingungen der Faltbarkeit der Pyramide mit sechs¬
Geometrische
eckiger
Basis
Bestimmung
3
des
Längenverhältnisses
Geometrische
zu n
:
2
0.33571 D
0.31623 D
n
von n
r—
Durchschlagsbedingungen
der Faltbarkeit der
Pyramide auf quadra-
tischer Basis:
Bestimmung des Längenverhältnisses
von n
zu
n
:
"1
n2
_2_
n
=
~
0.22975 D
0.31623 D
Die beiden
<
1
Bedingungen
zur
Faltung der Pyramide auf sechseckiger und auf
quadratischer Basis sind erfüllt.
V-36
Die
folgende Photosequenz zeigt die Veränderungen,
des
Faltvorgangs
die die Struktur während
durchmacht in der Aufsicht:
Bild 1:
Die
gefaltete Struktur;
die Stäbe liegen senk¬
recht zur Bildebene.
SP
Man beachte den Ver¬
gleichsmassstab
Bild 2:
Anfangsstadium der
Entfaltung
Bild 3:
Zwischenstadium der
Entfaltung
\
'^fl
V-37
S
^i Km
§*
SK
Bild 4:
Die beinahe entfaltete
Struktur
iSk
Bild 5:
Die entfaltete Struktur;
Man beachte den Ver¬
gleichsmassstab
V-38
Beispiel
2:
triangulierten abgestumpften Oktaeders,
Betrachten wir einen weiteren Teil des
das im
Gegensatz
Beispiel
zum
1
aus
vier ganzen
Pyramiden
sechseckiger
auf
auf
Basis, drei halben Pyramiden auf sechseckiger Basis und drei Pyramiden
quadratischer
Basis
gebildet
ist und somit einen höheren Grad
an
Komplexität
aufweist.
y>
Indem wir die Kanten durch Stäbe ersetzen, die in den Ecken
nander verbunden
sind, entsteht ein sphärisches Fachwerk
midalen Grundelementen auf
sechseckiger
und
¦
mitei¬
faltbaren pyra¬
viereckiger Basis.
«
m
m
aus
gelenkig
V-39
Geometrische
n
Eigenschaften
des Gebildes:
(Anzahl Stäbe)
n
=
0.31623 D
:
24
n
=
0.22975 D
:
12
n
=
0.33571 D
:
36
Anzahl Knoten im entfalteten Zustand
g
Anzahl Knoten während des
g
Faltvorgangs
=
28
=
30
Betrachten wir das Gebilde als räumlichen Mechanismus. Der
verändert sich
je nachdem, ob die beiden
Knoten
an
der
Preiheitsgrad
Spitze jedes Elementes
a) miteinander verbunden, oder b) voneinander getrennt sind.
a)
=
72
=
28
n
g
b)
F
=3g-n-6=6
n
=
72
=
38
g
=3g-n-6=36
F
Um das Gebilde durch
Bindungen
brauchen wir mindestens 6
+
6
an
=
12
System umzuwandeln,
den Grund in ein starres
Bindungen.
Schema:
Konstruktiv
gesehen, brauchen wir mindestens fünf Auflager.
V-40
Die
folgende Photosequenz zeigt die Veränderung, die die Struktur während des
Faltvorgangs
durchmacht in der Aufsicht:
.Bild 1:
Die gefaltete Struktur;
die Stäbe liegen senk¬
recht zur Bildebene
Bild 2:
Anfangsstadium
Entfaltung.
der
Die Knoten
der oberen Lage ent¬
fernen sich voneinander
und bilden eine Stern¬
form.
Bild 3:
—«—¦ä^sst"""^
AA^
Zwischenstadium der Ent¬
faltung. Sämtliche Punkte
des Gebildes entfernen
sich radial vom Zentrum
V-41
1
Ii
Bild 4j_
Zwischenstadium
der Entfaltung
01
» m
ffi
m
m
sn
m
¥a
Bild 5:
Die beinahe entfaltete
Struktur
1i
8
e5
s
M
^
Bild 6:
Die entfaltete Struktur
in der Aufsicht
V-42
DER EINFACH TRIANGULIERTE KUBUS
^
Man
beachte, dass in diesem Fall das Gebilde durch Aneinanderfügen
pyramidalen
Grundelementen auf
Basis
quadratischer
gebildet wird,
von
sechs
wobei die
Spitzen der einzelnen Pyramiden durch Projektion der Flächenmittelpunkte des
ursprünglichen Würfels auf die umgeschriebene Sphäre entstehen, und die Basen
der
pyramidalen
sprechen.
Grundelemente den Flächen des
ursprünglichen
Würfels ent¬
V-43
Beispiel 1:
Wir nehmen
aus
lichen sechs
diesem
Pyramiden
Polyeder einen Teil heraus,
baren
sind,
so
pyramidalen
aus
drei der
ursprüng¬
besteht.
Ersetzen wir die Kanten durch
verbunden
der
Stäbe, die in den Ecken gelenkig miteinander
dass ein räumliches Fachwerk
Elementen
zusammengesetzt ist.
I
^
entsteht, das
aus
drei falt¬
V-44
Eigenschaften
Geometrische
n
des Gebildes:
(Anzahl Stäbe) =21
n
=
0.57735 D
:
9
n
=
0.45970
:
12
D
Anzahl Knoten im entfalteten Zustand
g
Anzahl Knoten während des
g
Faltvorgangs
=
10
=
13
Betrachten wir das Gebilde als räumlichen Mechanismus. Der
je nachdem, ob die beiden
verändert sich
Knoten
an
der
Freiheitsgrad
Spitze jedes
Elementes
a) miteinander verbunden, oder b) voneinander getrennt sind.
a)
=
21
=
10
F
=
3g
n
=
21
=
13
=
3g
n
g
b)
g
F
Will
n
-
-
6
6
12
=
in ein starres Gebilde
Bindungen,
umwandeln,
so
Bindungen
braucht
man
Verankerungsstellen
sich mit drei festen
was
Geometrische
mit
-
das Gebilde im entfalteten Zustand durch
man
tionen)
n
-
Durchschlagsbedingungen
für die
Grund (Funda¬
zum
mindestens 3+6=9
erreichen lässt.
Faltung pyramidaler
Elemente
quadratischer Basis:
Verhältnis
von n
zu
n
:
"1
_2_
n
Die
=
~
0.45970 D
0.57735 D
Bedingung
<
±
ist erfüllt.
V-45
Die
folgende Photosequenz zeigt
von
Knoten und Stäben
vom
geordneten Vorgang
den
gefalteten
Zustand bis
zur
Verschiebung
der
vollständigen Entfaltung
der Struktur in Seitenansicht:
Bild 1:
Das
gefaltete Modell.
beachte, dass sämt¬
liche Knoten und Stäbe
um eine gemeinsame Achse
gruppiert sind
Man
Bild 2:
Die oben liegenden Knoten
entfernen sich auf radia¬
len Bahnen von der ge¬
meinsamen Achse
H
Bild 3:
Zwischenstadium der
Entfaltung.
Die unteren
Knoten entfernen sich
radial
von
ihrer
sprünglichen Lage
»
ur¬
V-46
Bild 4:
S
Wi
Zwischenstadium der
Entfaltung. Der
der Spitze hebt
Knoten
sich
heraus; die Basisknoten
werden in ihre
endgültige
Lage gesetzt
m
Bild 5:
S
Die beinahe entfaltete
Struktur
%m
m
:<
Bild 6:
Die vollständig ent¬
faltete Struktur.
Die zur Entfaltung der
Struktur
gelösten Bindun¬
gen werden hier wieder
fixiert
V-47
Beispiel
2:
Betrachten wir wiederum den einfach
triangulierten
Würfel:
y
Dieser kann in vier
Pseudopyramiden
Ebene liegen.
Pseudopyramiden mit sechseckiger Basis geteilt werden.
sind
pyramidale Elemente, deren Basispunkte nicht in einer
V-48
Pseudopyramidales
Wir nehmen
Grundelement mit
sechseckigem
dem oben beschriebenen
von
A und die Punkte B,
Grundriss
Polyeder den Teil, der durch die Spitze
C, D, E, F, G gebildet wird.
H
?
*N
io
n
1\
Die Referenzebene
E und G
=
TT
sei
gebildet durch die Punkte B,
liegen in einer Parallelebene
0.1494 D. Die
Spitze
zu
TT
Die Punkte C,
mit dem Abstand CC
A habe den Abstand AA'
wobei D der Durchmesser der dem
D und F.
=
0.2928 D
von
=
EE*
der Ebene TT,
ursprünglichen Polyeder umgeschriebenen
Sphäre ist. Die Projektion der pseudopyramidalen Figur auf die Ebene
ein
irreguläres
bildet
TT
Sechseck.
Ersetzen wir die Kanten durch
verbunden
GG'
=
Stäbe, die in den Ecken gelenkig miteinander
sind, und unterteilen wir die Spitze in die zwei
Knoten A und
H,
die alternierend durch radiale Stäbe mit den Ecken der Basis verbunden sind.
pyramidalen Elemente mit regulärer sechseckiger Basis definier¬
Die im Fall der
ten
der Faltbarkeit der sechs Stabketten werden hier
Bedingungen
gründen erfüllt.
aus
Symmetrie¬
V-49
Durchschlagsbedingungen:
=
1
n1
<
/
3
0.57735 D
0.45970 D
Gleichung
mit den
I
n2
II
/
3
bedeutet, dass die Spitze A, die durch die Stäbe
Eckpunkten C, E,
G der Basis verbunden
alternierend
ist, die Ebene
n2
durchschlagen
TT
kann.
Gleichung
II
bedeutet, dass die Spitze H, die in der Ausgangslage mit A iden¬
tisch ist und durch die Stäbe
bunden wird, die Ebene
TT
nicht
n
alternierend mit den
Eckpunkten
B, D, F
durchschlagen kann. Die Figur kann
ver¬
unter der
derjenige Punkt der Spitze ist, der die
Ebene TT durchschlägt. Dies bedeutet, dass A sich während der Faltung in die
Richtung des Mittelpunktes bewegen muss.
Bedingung gefaltet werden,
Nehmen wir das
dass A
gleiche Teilgebilde
des
triangulierten
Würfels wie im vorher¬
gehenden Beispiel. Dieses Mal betrachten wir aber einen Teil, der
pseudopyramidalen Grundelementen mit sechseckiger Basis besteht.
I /
J/
^
aus
drei
V-50
Geometrische
n
=
Eigenschaften:
21
Anzahl Knoten bei voll entfaltetem Zustand: g
Anzahl Knoten während des
Die kinematischen
Faltvorgangs:
Eigenschaften
vorgangs als auch bei voller
g
=
10
=
13
des Gebildes sind sowohl während des Falt¬
Entfaltung
ähnlich wie im
vorangehenden
Fall.
V-51
Die
folgende Photosequenz zeigt den geordneten Vorgang
Knoten und Stäben
vom
gefalteten
Zustand bis
zur
Verschiebung
der
von
vollständigen Entfaltung
der Struktur in Seitenansicht:
Bild 1:
1
Das
Man
gefaltete Modell.
beachte, dass sämt¬
liche Knoten und Stäbe
um eine gemeinsame Achse
gruppiert sind.
Bild 2:
Die oben
liegenden
Knoten entfernen sich
auf radialen Bahnen von
der gemeinsamen Achse.
SSss
Bild 3:
Zwischenstadium der
Entfaltung.
Die unteren
Knoten entfernen sich
I
radial
von
ihrer
ur¬
sprünglichen Lage.
.V-52
Bild 4:
Zwischenstadium der
Entfaltung. Der
der Spitze hebt
Knoten
sich
allmählich heraus.
Bild 5:
Zwischenstadium der
Die Basis¬
knoten werden in ihre
Entfaltung.
endgültige Lage gesetzt.
Bild 6:
Die
vollständig
ent¬
faltete Struktur.
Die
zur
Entfaltung
der
Struktur gelösten Bindun¬
gen werden wieder fixiert.
V-53
DER DOPPELT TRIANGULIERTE KUBUS
Beispiel
1:
Pseudopyramidales Grundelement mit viereckiger Basis.
Polyeder nehmen wir einen Teil,
Spitze A gebildet wird.
Von dem vorher beschriebenen
Punkte B, C, D, E und die
<5*\
•>>
der durch die
V-54
Wir ersetzen die Kanten durch
Analog
verbunden sind.
teilen wir die
zum
Stäbe, die in den Ecken gelenkig miteinander
Fall der
Spitze in zwei
Pyramide mit viereckiger Basis
Knoten A und
unter¬
F, die alternierend durch radiale
Stäbe mit den Knoten der Basis verbunden sind.
Die im Fall des
pyramidalen Elementes mit quadratischer Basis definierten
Bedingungen der Faltbarkeit der vier Stabketten werden hier
Symmetrie¬
aus
gründen erfüllt.
Durchschlagsbedingungen:
"1
0.38268 D
0.45970 D
<
1
0.30291 D
0.45970 D
<
1
Gleichung
mit den
I
II
bedeutet, dass die Spitze A, die durch die Stäbe
Eckpunkten
C und E der Basis verbunden
alternierend
ist, die Ebene
n
durchschla¬
TT
gen kann.
Gleichung
II
bedeutet, dass die Spitze F, die in der Ausgangslage mit A iden¬
tisch ist und durch die Stäbe
nierend verbunden
n
ist, die Ebene
mit den
TT
B und D der Basis alter¬
Eckpunkten
ebenfalls
durchschlagen kann.
Gegeben sei ein Teil des doppelt triangulierten Kubus,
gende Gebilde ergibt, das
scher Basis besteht.
aus
vier
pseudopyramidalen
so
dass sich das fol¬
Elementen mit
quadrati¬
V-55
77
Ersetzen wir die Kanten durch
so
Stäbe, die gelenkig miteinander verbunden sind,
entsteht, das sich
dass ein räumliches Fachwerk
aus
vier faltbaren pyra¬
midalen Elementen zusammensetzt.
Geometrische
n
Eigenschaften:
28
(Anzahl Stäbe)
n
=
0.45970 D
n
=
0.38268 D
n
=
0.30291 D
:
12
:
8
Anzahl Knoten bei entfaltetem Zustand:
g
Anzahl Knoten während des
g
Faltvorgangs:
=
13
=
17
Betrachten wir das Gebilde als räumlichen Mechanismus. Der
Freiheitsgrad
je nachdem, ob die beiden Knoten an der Spitze jedes Elementes
a) miteinander verbunden, oder b) voneinander getrennt sind.
verändert sich
V-56
a)
n
=
=
13
=
3g-n-6=
g
b)
n
=
g
=
F
Will
28
man
=
5
28
17
3g-n-6=17
das Gebilde in entfaltetem Zustand durch
tionen) in ein starres System umwandeln,
Bindungen. Konstruktiv wird
man
so
Bindungen
braucht
das aber durch vier
man
zum
Grund (Funda¬
mindestens 5
6
+
Verankerungsstellen
je drei Bindungen lösen, also durch insgesamt 12 Bindungen.
s
\
=
mit
11
V-57
Wie bei früheren
Vorgang
der
Beispielen zeigt die folgende Photosequenz den geordneten
Verschiebung
vollständigen Entfaltung
von
Knoten und Stäben
vom
gefalteten Zustand bis
zur
der Struktur in Seitenansicht.
Bild 1:
Das
gefaltete Modell.
Sämtliche Knoten und
Stäbe sind um eine
gemeinsame Achse grup¬
piert.
Bild 2:
I
K
I
St
?,
Die oben liegenden
Knoten entfernen sich
auf radialen Bahnen von'
der gemeinsamen Achse.
Bild 3:
Zwischenstadium der
Die unteren
Entfaltung.
Knoten entfernen sich
'radial
von
ihrer
ur¬
sprünglichen Lage.
»
V-58
Bild 4
^5
Die Basisknoten werden
in ihre
gesetzt
endgültige Lage
Bild 5:
Die
^
vollständig entfalte¬
te Struktur. Die zur Fal¬
tung der Struktur ge¬
lösten Bindungen werden
wieder fixiert
V-59
Beispiel
Analog
2:
zum
vorangehenden Fall gehen wir
vom
doppelt triangulierten Kubus
aus:
Jede Fläche des
tion in ein
ursprünglichen Kubus wandelt sich durch doppelte Triangula¬
pseudopyramidales
Gebilde mit
triangulierte Kubus lässt sich also
Grundelementen zusammensetzen.
aus
doppelt
pseudopyramidalen
achteckiger Basis
insgesamt sechs
um.
Der
V-60
PSEUDOPYRAMIDALE ELEMENTE MIT ACHTECKIGER BASIS
Nehmen wir den Teil des
die
Spitze
A
Polyeders, der durch die Punkte B,C,D,E,F,G,H,I und
gebildet wird.
*\
c*-j
J)
«sr-s
y
1
Die
Projektion der pseudopyramidalen Figur
Seitenlänge
läres Achteck mit der
n
auf die Ebene TT bildet ein
und den alternierenden Radien
n
irregu¬
und
n
.
Wir ersetzen die Kanten durch
verbunden sind.
wir die
Analog
zum
Stäbe, die in den Ecken gelenkig miteinander
Fall der Pyramide mit achteckiger Basis unterteilen
Spitze der Pyramide in die zwei
Knoten A und
J, die alternierend durch
radiale Stäbe mit den Knoten der Basis verbunden sind.
Die beim Fall des
nierten
pyramidalen Elementes mit regulärer achteckiger Basis defi¬
Bedingungen der Faltbarkeit für die acht viergliedrigen Stabketten
werden hier
aus
Symmetriegründen erfüllt.
V-61
Durchschlagsbedingungen:
0.38268 D
0.30291 D
<
TT
0.45970 D
0.30291 D
>
TT
Gleichung
mit den
I
ii
bedeutet, dass die Spitze A, die durch die Stäbe
Eckpunkten C, E, G,
I der Basis verbunden
alternierend
n
ist, die Ebene
durch¬
TT
schlagen kann.
Gleichung
II
bedeutet,
ist und durch die Stäbe
n
alternierend mit den
Basis verbunden ist, die Ebene
Die
Figur kann also
Punkt der
Spitze J, die in der Ausgangslage identisch
dass die
nur
Eckpunkten B, D, F,
H der
durchschlagen kann.
TT
unter der
Bedingung gefaltet werden ,dass
Spitze ist, der die Ebene
TT
durchschlägt.
A
derjenige
V-62
Wir nehmen
denjenigen Teil
des
triangulierten Kubus, der
unvollständigen Pseudopyramiden
und vier
Wir ersetzen die Kanten durch
verbunden
sind,
so
mit
achteckiger
einer ganzen
Basis besteht.
Stäbe, die in den Ecken gelenkig miteinander
dass ein räumliches Fachwerk
Grundelementen entsteht.
aus
aus
faltbaren
pyramidalen
V-63
Geometrische
n
Eigenschaften:
(Anzahl Stäbe)
=
n
=
0.45970 D
:
20
n
=
0.38268 D
:
16
n
=
0.30291
:
16
D
52
Anzahl Knoten im entfalteten Zustand
Anzahl Knoten während des
:
Faltvorgangs:
g
g
=
21
=
26
Betrachten wir das Gebilde als räumlichen Mechanismus. Der
verändert sich
je nachdem, ob die beiden
Knoten
an
der
Freiheitsgrad
Spitze jedes
Elementes
a) miteinander verbunden, oder b) voneinander getrennt sind.
a)
n
g
F
b)
n
g
F
Will
=
52
=
21
=
3g-n-6
=
52
5
=
26
=
3g-n-6=20
man
das Gebilde im entfalteten Zustand durch
tionen) in ein
11
=
starres
System umwandeln,
so
Bindungen
benötigt
man
zum
Grund (Funda¬
mindestens 5
+
6
Bindungen. Konstruktiv wird man das aber durch vier Verankerungsstellen
mit je drei Bindungen lösen, d.h. durch insgesamt 12 Bindungen.
=
V-64
Die
folgende Photosequenz zeigt
Knoten und Stäbe
vom
den
geordneten Vorgang der Verschiebung der
gefalteten Zustand bis
zur
vollständigen Entfaltung
der
Struktur in Seitensicht.
Bild 1:
I
gefaltete Modell.
Sämtliche Knoten und
Stäbe sind um eine ge¬
meinsame Achse gruppiert.
Das
Bild 2:
m
m
Die oben liegenden Knoten
entfernen sich auf radia¬
len Bahnen von der ge¬
YA
meinsamen Achse.
VA
Bild 3:
SS
1\
Zwischenstadium der
Entfaltung. Die unteren
Knoten entfernen sich
1
radial
von
ihrer
ur¬
sprünglichen Lage.
V-65
Bild 4:
Zwischenstadium der
Entfaltung. Der Knoten
in der Spitze hebt sich
heraus, und die Basis¬
I
knoten werden in ihre
endgültige Lage gesetzt.
m
s
m
4y^
Bild 5
ms
:
Die beinahe entfaltete
Struktur
m
m
m
m
Bild 6:
m
m
f
Die vollständig ent¬
faltete Struktur.
Die zur Entfaltung der
Struktur gelösten Bindun¬
gen werden wieder fixiert.
V-66
DAS DOPPELT TRIANGULIERTE PENTAGONDODEKAEDER
i
Pseudopyramidales
Wir nehmen
und die
Grundelement mit
viereckigem Grundriss
denjenigen Teil des Polyeders, der durch die Punkte B, C, D,
Spitze
A
begrenzt wird.
<£b
E
V-67
Wir ersetzen die Kanten durch Stäbe, die in den Ecken
verbunden sind und unterteilen
Basis die
analog
zum
Spitze der Pyramide in die zwei
Fall der
gelenkig miteinander
Pyramide mit viereckiger
Knoten A und
F, die durch radiale
Stäbe alternierend mit den Knoten der Basis verbunden sind.
Die im Fall des
pyramidalen
Elementes mit
viereckiger Basis definierten
Bedingungen der Faltbarkeit der vier Stabketten werden auch hier aus Symmetrie¬
gründen erfüllt.
Durchschlagsbedingungen
0.27327 p
0.32043 D
0.18142 D
0.32043 D
Die
1
<
1
Durchschlagsbedingungen
Knoten F
TT
<
II
sind sowohl für den Knoten A als auch für den
erfüllt, d.h. die Figur kann unabhängig davon, ob
A oder F die Ebene
durchschlägt, gefaltet werden.
doppelt triangulierte Pentagondodekaeder, dessen geometrische
Eigenschaften bereits definiert sind. Man beachte, dass das Polyeder aus 30
pseudopyramidalen Grundelementen mit viereckiger Basis zusammengesetzt ist.
Nehmen wir das
Von diesem
Polyeder nehmen wir denjenigen Teil, der
Elementen mit
aus
fünf
pseudopyramidalen
quadratischer Basis besteht.
^
V-
Das
geometrische Gebilde wird in ein faltbares Fachwerk umgewandelt, das
aus
vier Modularen Grundelementen zusammengesetzt ist.
E"
Geometrische
n
Eigenschaften:
(Anzahl Stäbe) =35
n
=
0.32043
D
:
10
n
=
0.27327 D
:
10
n
=
0.18142
:
15
D
Anzahl Knoten im entfalteten Zustand:
Anzahl Knoten während des
g
Faltvorgangs: g
=
16
=
21
Betrachten wir das Gebilde als räumlichen Mechanismus. Es hat
folgenden
Frei¬
heitsgrad:
a)
b)
n
=
35
g
=
16
F
=
3g-n-6=7
n
=
35
g
=
21
F
=
3g
Will
man
-
das Gebilde im entfalteten Zustand durch Fundationen in ein starres
System umwandeln,
wird
15
man
22
n
so
das durch 5
Bindungen total.
benötigt
man
mindestens 7
Verankerungsstellen
mit
+
6
=
13
Bindungen.
Konstruktiv
je 3 Bindungen lösen, d.h.
mit
V-69
Die
folgende Photosequenz zeigt
Knoten und Stäbe
vom
den
geordneten Vorgang
gefalteten Zustand bis
zur
der
Verschiebung
der
vollständigen Entfaltung
der
Struktur in Seitensicht.
«
1
/Bild 1:
Das gefaltete Modell.
Alle Knoten und Stäbe
sind
eine
gemeinsame
gruppiert.
um
Achse
Bild 2:
Die oberen Knoten ent¬
fernen sich radial von
der
£
gemeinsamen Achse.
l
£
Bild 3:
Zwischenstadium
der Entfaltung
l
V-70
Wi
I
Bild 4:
«
Die unteren Knoten ent¬
fernen sich radial von
ihrer
ursprünglichen Lage.
Bild 5:
^
Die vollständig entfaltete
Struktur. Die zur Ent¬
faltung
der Struktur ge¬
Bindungen werden
wieder fixiert.
lösten
V-71
Polyeder
Vom vorher beschriebenen
nehmen wir den
Teil, der durch die Punkte
B, C, D, E, F, G und die Spitze A begrenzt wird.
Die
so
entstandene
eckigem Grundriss,
Figur bildet ein pseudopyramidales Grundelement mit sechs¬
auf die Ebene TT ein
Projektion
dessen
ist. Man beachte, dass das
Polyeder
20
aus
zusammengesetzt ist.
*\
(H
LO
irreguläres Sechseck
pseudopyramidalen
Grundelementen
V-72
Ersetzen wir die Kanten durch
verbunden sind.
Analog
zur
Stäbe, die in den Ecken gelenkig miteinander
Pyramide mit sechseckiger Basis wird die Spitze in
die zwei Knoten A und H unterteilt, die alternierend durch radiale Stäbe mit
den Knoten der Basis verbunden sind.
Die
Bedingungen der Faltbarkeit der sechs Stabketten werden hier
gründen
aus
Symmetrie¬
erfüllt.
Durchschlagsbedingungen:
n3
n2
0.18142 D
0.27327 D
1
0.32043 D
0.27327 D
n2
Gleichung
I
<
^
>
_
2
2
II
-=—
,_
bedeutet, dass die Spitze A, die durch die Stäbe
mit den Knoten G, E, G der Basis verbunden ist, die Ebene
TT
n
alternierend
durchschlagen
kann.
Gleichung
II
bedeutet, dass die Spitze H, die in der Ausgangslage mit A iden¬
tisch ist und durch die Stäbe
verbunden ist, die Ebene
Figur
der
nur
unter der
Spitze ist,
TT
alternierend mit den Knoten B, D, F der Basis
n
nicht
durchschlagen kann.
Bedingung gefaltet
der die Ebene
TT
Das
heisst, dass die
werden kann, dass A
durchschlägt.
derjenige
Knoten
V-73
Nehmen wir den Teil des
aus
fünf
doppelt triangulierten Pentagondodekaeders,
pseudopyramidalen Elementen
mit
sechseckiger Basis
der
besteht:
77
Ersetzen wir das
geometrische Gebilde
folgendes faltbare
durch fünf faltbare
Fachwerk entsteht:
P
Elemente,
so
dass
V-74
Eigenschaften:
Geometrische
n
(Anzahl Stäbe)
50
=
n
=
0.32043 D
:
15
n
=
0.27327 D
:
20
n
=
0.18142 D
:
15
Anzahl Knoten im entfalteten Zustand
Anzahl Knoten während des
:
Faltvorgangs:
g
21
g
26
Betrachten wir das Gebilde als räumlichen Mechanismus mit
folgendem Freiheits¬
grad:
a)
b)
n
=
50
g
=
21
F
=
3g
n
=
50
g
=
26
=
3g
F
-
-
n
n
6
=
6
=
-
-
Es sind demnach 7 + 6
starres
7
22
=
13
Bindungen erforderlich,
System umzuwandeln. Konstruktiv wird
stellen mit
je
drei
Bindungen realisieren,
man
was
15
um
das
das Gebilde in ein
jedoch
mit fünf
Bindungen ergibt.
Auflager¬
V-75
Die
folgende Photosequenz zeigt
Knoten und Stäben
vom
den
gefalteten
geordneten Vorgang der Verschiebung
Zustand bis
zur
von
vollständigen Entfaltung
der
Struktur in Seitensicht.
Bild 1:
!
Das
gefaltete Modell.
Alle Knoten und Stäbe
sind um eine gemeinsame
Achse
gruppiert.
Bild 2:
Die oberen Knoten ent¬
fernen sich radial von
der gemeinsamen Achse.
S5
i
WA
Sl
^
Bild 3:
Zwischenstadium der
1
i
Entfaltung
**s
ftm
V-76
I
3ild 4
W
Die unteren Knoten ent¬
fernen sich radial von
ihrer
ursprünglichen Lage
Bild 5:
Die vollständig entfaltete
Struktur. Die zur Entfal¬
m
tung der Struktur ge¬
lösten Bindungen werden
wieder fixiert
V-77
Beispiel 3:
Pseudopyramidales Grundelement mit zehneckiger Basis:
Vom oben beschriebenen Polyeder nehmen wir den Teil, der durch die Punkte
B, C, D, E, F, G, H, I, J, K und die Spitze A begrenzt wird. Die Projektion
des pseudopyramidalen Grundelementes auf die Ebene TT bildet ein irreguläres
Zehneck.
V-78
Polyeder besteht
Der
aus
12
pseudopyramidalen Elementen mit zehneckiger Basis,
Stäbe, die
Ersetzen wir die Kanten durch
verbunden sind, und unterteilen die
in den Ecken
gelenkig miteinander
Spitze in die zwei
Knoten A und
L, die
durch radiale Stäbe alternierend mit den Knoten der Basis verbunden sind.
Die
Bedingungen der Faltbarkeit der verschiedenen Stabketten werden
aus
Sym¬
metriegründen erfüllt.
Durchschlagsbedingungen:
n2
n3
"¦
nl
"
"
n3
0 27327 D
0 18142 D
<
0 32043 D
0 18142 D
>
Gleichung
1.7013
1.7013
II
bedeutet, dass die Spitze A, die durch die Stäbe
I
alternierend
n
mit den Knoten C, E, G, I, K der Basis verbunden ist, die Ebene
durchschla¬
TT
gen kann.
Gleichung
II
bedeutet,
dass die
tisch ist und durch die Stäbe
Figur
Knoten der
nur
unter der
A iden¬
alternierend mit den Knoten B, D, F, H, J
ist, die Ebene
der Basis verbunden
dass die
n
Spitze L, die in der Ausgangslage mit
TT
nicht
durchschlagen kann.
Bedingung gefaltet werden kann,
Spitze ist, der die Ebene
TT
durchschlägt.
heisst,
Das
wenn
A
derjenige
V-79
Nehmen wir
vom
doppelt triangulierten Pentagondodekaeder den Teil, der
einem ganzen und fünf
eckiger
unvollständigen pseudopyramidalen Elementen
aus
mit zehn¬
Basis besteht.
\\y7'
7
<
I
r \
•-
\
\}
Ersetzen wir das
so
dass das
geometrische Gebilde
folgende
5*
durch
entsprechende faltbare Elemente,
faltbare Fachwerk entsteht:
%
m
<S
fl
V-80
Geometrische
n
Eigenschaften:
(Anzahl Stäbe)
=
65
n
=
0.32043 D
:
25
n
=
0.27327 D
:
20
n
=
0.18142
:
20
D
Anzahl Knoten im entfalteten Zustand:
Anzahl Knoten während des
g
Faltvorgangs: g
=
26
=
32
folgendem
Betrachten wir das Gebilde als räumlichen Mechanismus mit
Freiheits¬
grad:
a)
n
g
=
=
26
=
3g
=
65
=
32
=
3g-n-6=25
F
b)
65
n
g
F
-¦
n
--
6
Es sind demnach 7 + 6
starres
fünf
17
=
13
=
Bindungen erforderlich,
System umzuwandeln.
Verankerungsstellen
um
das Gebilde in ein
mit
Aus konstruktiven Gründen wird
man
je drei Bindungen realisieren.
das aber durch
V-81
Die
folgende Photosequenz zeigt den geordneten Vorgang der Verschiebung
Knoten und Stäben
gefalteten Zustand bis
vom
zur
von~
vollständigen Entfaltung
der Struktur in Seitensicht.
Bild 1:
Alle Knoten und Stäbe
sind um eine gemeinsame
Achse
gruppiert.
Bild 2:
Die oberen Knoten ent¬
fernen sich radial von
der gemeinsamen Achse.
Ssss
Va
^
Bild 3
K!
I
11
:
Zwischenstadium der
Entfaltung
V-82
Bild 4
Zwischenstadium der
Entfaltung
AB
SPüi
R
Bild 5:
0
SSÄ
4
Die unteren Knoten ent¬
fernen sich radial von
&
ihrer
ursprünglichen Lage
WA
'A
a
1
m
Bild 6
1
fe:
«
t^
Die vollständig ent¬
faltete Struktur.
Die zur Entfaltung der
Struktur
gelösten
Bindun¬
gen werden wirder fixiert
V-83
DAS DOPPELT TRIANGULIERTE ABGESTUMPFTE IKOSAEDER
Das Gebilde besteht
und
aus
20
aus
12
pseudopyramidalen Elementen mit zehneckiger Basis
pseudopyramidalen Elementen mit zwölfeckiger Basis.
V-84
Pseudopyramidales Grundelement mit zehneckiger Basis
Nehmen wir den Teil des
Polyeders, der durch die Punkte B, C, D, E, F, G, H,
I, J, K und die Spitze A bzw. L begrenzt wird.
(L)
"3
Die
Projektion des pseudopyramidalen Grundelementes auf die Referenzebene
bildet ein
TT
irreguläres Zehneck.
Ersetzen wir die Kanten durch
verbunden sind,
so
Stäbe, die in den Ecken gelenkig miteinander
erhalten wir ein Modulares Grundelement
analog
zum voran¬
gehenden Beispiel.
Die
Bedingungen für die Faltbarkeit der einzelnen Stabketten sind
metriegründen erfüllt.
Durchschlagsbedingungen:
n_
0.17431 D
0.10141
n,.
n.
D
0.14325 D
0.10141 D
<
1.7013
>
1.7013
II
aus
Sym-
-
V-85
Gleichung
bedeutet, dass der
I
Knoten A der
Spitze, der durch die Stäbe
n
alternierend mit den Knoten C, E, G, I, K der Basis verbunden ist, die Ebene
durchschlagen
Gleichung
II
kann.
bedeutet, dass die Spitze L, die in der Ausgangslage mit
tisch ist und durch die Stäbe
Figur
Knoten der
nur
n
unter der
A iden¬
alternierend mit den Knoten B, D, F, H, J
ist, die Ebene
der Basis verbunden
dass die
TT
TT
nicht
durchschlagen kann.
Bedingung gefaltet
Spitze ist, der die Ebene
TT
werden
kann,
bedeutet,
Das
wenn
A
derjenige
durchschlägt.
Pseudopyramidales Grundelement mit zwölfeckiger Basis
Von dem oben beschriebenen
Polyeder nehmen wir den Teil, der durch die Punkte
E, F, G, M, N, 0, P, Q, R, S, T, U und die Spitze V begrenzt wird. Es handelt
sich dabei
pseudopyramidales Modulares Grundelement, dessen Basispunkte
nicht in einer Ebene liegen.
um
ein
w
Die
Projektion
bildet ein
des
pseudopyramidalen Grundelementes
TT
irreguläres Zwölfeck.
Ersetzen wir die Kanten durch
verbunden
auf eine Referenzebene
Stäbe, die in den Ecken gelenkig miteinander
sind, und unterteilen wir die Spitze in zwei Knoten, die durch radia¬
le Stäbe alternierend mit den Knoten der Basis verbunden sind.
V-86
Die
Bedingungen
Symmetriegründen
für die Faltbarkeit der verschiedenen Stabketten werden
aus
erfüllt.
Durchschlagsbedingungen:
0.17541
0.10141
D
D
0.20621 D.
0.10141 D
Das
<
2
>
2
bedeutet, dass der Knoten Z der Spitze, der durch die Stäbe
mit den Knoten E, G, N, P. R, T der Basis verbunden
Knoten V die Ebene TT
durchschlagen kann.
Bedingung faltbar, dass
Z
derjenige
n
ist, im Gegensatz
Das Gebilde ist demnach
Knoten der
alternierend
nur
zum
unter der
Spitze ist, der die Ebene
TT
durchschlägt.
Vom
aus
doppelt triangulierten abgestumpften Ikosaeder nehmen wir den Teil, der
fünf ganzen und fünf unvollständigen pseudopyramidalen Elementen mit zwölf¬
eckiger Basis sowie sechs pseudopyramidalen Elementen mit zehneckiger Basis
zusammengesetzt ist:
V-87
Geometrische
n
Eigenschaften:
(Anzahl Stäbe) =235
0.10141 D
:
80
=
0.14325 D
:
30
n
=
0.17431 D
:
30
n
=
0.17541 D
:
50
=
0.20621 D
:
45
n
n2
n
=
Anzahl Knoten beim entfalteten Zustand: g
Anzahl Knoten während des Faltvorgangs: g
=
=
86
102
Betrachten wir das Gebilde als räumlichen Mechanismus mit
folgendem
Freiheits¬
grad:
a)
b)
n
=
235
g
=
86
F
=
3g-n-6=17
n
=
235
g
=
102
F
=
3g-n-6=65
Es sind demnach 17+6
System umzuwandeln.
Bindungen erforderlich,
das Gebilde in ein starres
um
Aus konstruktiven Gründen wird
ankerungsstellen mit je
drei
Bindungen lösen.
man
das aber mit 10 Ver¬
V-88
folgende Photosequenz zeigt den geordneten Vorgang der Verschiebung von
Knoten und Stäben vom gefalteten Zustand bis zur vollständigen Entfaltung
Die
der Struktur in Seitensicht.
Bild 1:
Alle Stäbe und Knoten
sind
um
Achse
eine
gemeinsame
gruppiert.
Bild 2:
Die oberen Knoten ent¬
fernen sich radial von
der gemeinsamen Achse.
m
Bild 3
:
Zwischenstadium der
Entfaltung.
1
I
5^§§S
m. 7&
t>4^~
V-89
Bild 4:
Zwischenstadium der
5S
«
m
i
s*
Entfaltung.
iim
'«&
MSm.
v^
I»
s^
fij
^s-
Bü
JSfi IN
ü
pI
%
i
BB
HT
^
^
^
i
¦
l
§£
ob
fi
i
¦ÄV §« 1'iJ
SB
S
0
Bild 5:
^
gs
a
5*
I
Die unteren Knoten ent¬
fernen sich radial von
ihrer ursprünglichen Lage.
I
|gS5
Bild 6:
ga^gr^
b
Die vollständig ent¬
faltete Struktur. Die zur
.Entfaltung der Struktur
gelösten Bindungen werden
wieder fixiert.
V-90
WEITERE TEILUNGSARTEN DER SPHAERE
Die Gemeinsamkeit der bis
besteht
geht,
darin, dass
aus
welchem
jetzt besprochenen Methoden
zur
Teilung
der
Sphäre
jeweils von einem der fünf platonischen Körper aus¬
dadurch, dass man ihn direkt oder nach seiner Abstump¬
man
man
fung trianguliert, einen geometrischen
Grundraster
zur
Bildung faltbarer
Strukturen erhält.
beachte, dass
Man
es
möglich ist, jedes
metrischen Gebilde oder
einzelne der vorher behandelten geo¬
pseudopyramidalen Elemente mit viereckiger Basis
zu
unterteilen.
folgenden
Im
Abschnitt möchten wir auf diese Modularen Elemente genauer ein¬
gehen, indem wir sie einerseits für weitere Teilungsarten der Sphäre und
dererseits als Grundelemente
zur
Faltung
anderer einfach oder
an¬
doppelt ge¬
krümmter Flächen verwenden.
Pyramidale oder pseudopyramidale Grundelemente mit viereckiger Basis
Die verschiedenen Arten
von
sich durch die Form ihres
pyramidalen Elementen mit viereckiger Basis lassen
Basispolygons unterscheiden.
So erhalten wir pyra¬
midale Elemente mit
-
-
-
-
quadratischer Basis
rhombischer Basis
trapezoidaler Basis
irregulärer viereckiger Basis.
Untersuchen wir das
pyramidale Element mit trapezoidaler Basis im Hinblick
auf seine
zur
Die
Anwendung
Faltung sphärischer
Sphäre wird durch zwei Scharen
len und die andere
geteilt.
aus
von
Fachwerke.
Kreisen,
von
denen die eine
meridianen Kreisen besteht, in
aus
paralle¬
sphärische Trapeze ein¬
V-91
DIE IN TRAPEZE EINGETEILTE SPHAERE
Entsprechend können wir ein Polyeder bilden, das
aus
Trapezen besteht;
die oberste und die unterste,Kalotte mit dem Zentrum in den Polen des
nur
Poly¬
eders sind davon ausgenommen: sie bilden Dreiecke. Die Anzahl Flächen des
Polyeders wird
durch die Anzahl Meridianen M und der
parallelen Kreise
P wie
folgt bestimmt:
F
=
2-M-P
Es stellt sich die
den muss,
Frage, wie die Triangulation des Gebildes vorgenommen wer¬
damit pyramidale Elemente entstehen, die gefaltet werden können.
V-92
Man kann durch einfache
Triangulation pyramidale
Basis erhalten. Es stellt sich die
die umhüllende
trapezoidaler
Frage, welcher Punkt des Basistrapez auf
werden
soll, damit das
so
entstandene Ele¬
gefaltet werden kann.
ment
Zur
Sphäre projiziert
Elemente mit
Beantwortung dieser Fragen müssen zunächst die Bedingungen untersucht
werden, die für die Faltbarkeit der einzelnen Stabketten definiert wurden.
IF)
/
(F)
T
/
'7
Damit die vier Stabketten ACBE, AEDC, FBED, FDCB faltbar sind, müssen die
folgenden Gleichungen erfüllt sein:
V-93
AC
-
AE
-
CB
BE
-
EA
=
0
ED + DC
-
CA
=
0
+
FB-BE+ED-DF=0
FD-DC+CB-BF=0
Diese
als
Gleichungen wurden
Voraussetzung
aber wegen der
jetzt
bis
zusammen
Durchschlagsbedingungen
mit den
Faltung pyramidaler Elemente
für die
berücksichtigt,
immer
Symmetrie der faltbaren Elemente wurden die Gleichungen immer
stark vereinfacht.
Es soll eine
Pyramide mit trapezoidaler Basis gebildet werden, bei der das
Verhältnis der
Kantenlängen die Bildung eines zusammenfaltbaren Modularen
Elementes erlaubt. Gehen wir davon aus, dass die
Kantenlängen
Trapezes und der Abstand h der Spitze der Pyramide
Pyramide)
bekannt sind. Unbekannt sind die Kanten
die vorher definierten
man
unter
genden
zur
e
a,
b,
c
des
Basisebene (Höhe der
und d der
Pyramide.
Wenn
Bedingungen der Faltbarkeit angewendet werden, erhält
Berücksichtigung des symmetrischen Charakters des Gebildes die fol¬
Gleichungen:
zwei
AC
CB + BE
-
EA
-
=
0
I
d-c+b-e
FB
BE + ED
-
=0
DF
-
=
0
II
d-b
Das
ergibt
die
I
folgende Beziehung:
II
-
-*
-a
b
I
+
II
->
Dazu kommt die
+
c
-
2b
=
0
a + C
III
=
2d-c+a-2e
d
und
=0
+ a-e
=
e
+
£-2-a-
=
0
IV
geometrische Bedingung, die sich durch die Lage des Punktes A1,
Projektion der Pyramidenspitze auf die Symmetrieachse der Basis ergibt:
f
=
f±
+
f2
,
v
V-94
wobei
f, f
und f
als Funktion
Gleichung
können. In
von
eingesetzt,
V
a,
b,
c,
und unter
d,
und h
e
ausgedrückt werden
Berücksichtigung
Gleichungen
der
III und IV resultiert eine
Unbekannte ist. Mit Hilfe
eines numerischen
die
Gleichung, in der e die
Annäherungsverfahrens lässt sich
Gleichung
nach
e
lösen.
Beispiel
Anwendung der vorher ermittelten Prinzipien
der
midaler Grundelemente mit
trapezoidaler Basis
zur
Faltung
zur
Bildung pyra¬
eines
sphärischen
Fachwerks
Gehen wir
ebenen M
einer halben
von
Sphäre mit dem Radius
6 aus, haben wir
=
R
c
60
IC.
Aus der
a
bl
Aus
III erhält
Gleichung
1
=
+ c
man:
1
geometrischen Gründen erhält
=
R
r
=
R
a
=
r
C1
b
=
coscj)
=
2 R
R
coscp
sin
9l
—
man:
R und der Anzahl Meridian¬
V-95
In
Gleichung
sin
—-
=
und nach sin—
./2-1
=
48.939660
a,
=
0.656885
D
b.
=
0.82847
D
cn
=
9*.
Analog
eingesetzt
III
D
dazu erhalten wir:
ül
?<
60
\1
c„
=
a
r„
=
R
r2
=
R
cos9
coscp
=
R
coscp
92-9-L
2R sin(—-—)
=
0.65685 D
aufgelöst erhalten wir:
V-96
In
Gleichung
2 sin
4
eingesetzt:
III
9 -cp
(-V^)
92"9X
sin(—-—)
9
-*
Analog
cos9
=
cos9
-
75.277161
0.25423 D
b
=
0.45554 D
c
=
0.65685 D
dazu eine weitere
4 sin(—-—)
9
a
b
c3
=
VI
cos9
-
=
a2
cos9
+
-„
=
-
Teilung
cos9
-
mit einer Parallelebene:
cos9
=
0
VII
85.04247
=
0.08642 D
=
0.17033 D
=
0.25423 D
Um die oberste Kalotte
(Abschlusskalotte) zu triangulieren, bilden wir ein
faltbares
pyramidales Element mit sechseckiger Basis, das zwischen die sechs
obersten trapezoidalen Pyramiden eingesetzt wird.
^?>
<2
J>
V-97
Allgemein können wir sagen:
Gegeben
und der Anzahl Meridianebenen M.
I
\'
die
sphärische Kalotte,
sei eine
gekennzeichnet
ist durch
9
,
R
i
\u
7
fe
:3
[£
So erhalten wir:
6
»
Die
2TT
="m"
Gleichungen
VI und VII können
'i+l
"
4 sin(-
i variiert
von
folgt:
-
COS9.
-
COS9.
0
=
i=l bis i=P, wobei P die Anzahl Parallelebenen ist. Diese
Gleichung ermöglicht
Daraus
9i.
allgemein ausgedrückt werden:
r.
=
c.
=
1.
1
R
=
=
gegebenes 9.,
<P.+1
zu
ermitteln.
C0S9.
6
1
b.1
uns, für ein
2 r. sin
1
2
=
—
2 R sm(
2 R C0S9.
Ti
sin
6
—
2
)
2
2 R cos9.
sin
Ti+1
2
—
.
Bestehen die Werte a., b. und c.,
11
1
so
ist
es
unter
Berücksichtigung der
v_c
möglich, die vorhandenen
Werte in V einzusetzen und diese
Gleichung
IV
Gleichung
V mit Hilfe eines numerischen
lösen, wobei
gedrückt wird,
ist, dass h als Funktion
bemerken
zu
unter
Berücksichtigung
füllt sein müssen, damit die
zu
liegen
Annäherungsverfahrens nach
Spitze
der
der
9
I
Eigenschaften:
(Anzahl Stäbe)
=
114
Anzahl Knoten im entfalteten Zustand
Anzahl Knoten während des
Es
ergibt
sich
F=3g-n-6=9
b)
F
3g
-
n
Faltvorgangs:
folgender Freiheitsgrad:
a)
=
:
-
6
=
66
b.,
c.
und e.
aus-
1
die
er¬
=0, M=6, P=3 die folgende
fc
a
,
111
geometrischen Beziehungen,
faltbare Struktur:
Geometrische
a
zu
Pyramide auf die Fläche der Sphäre
kommt. Dadurch erhalten wir für
K
von
e.
g
43
g
62
V-99
Die
folgende Photosequenz zeigt
die
Entfaltung
der Struktur
am
Modell:
Bild 1:
Die
gefaltete
Struktur
Bild 2:
l
ü
Zwischenstadium der
Entfaltung
Va
VA
3-
Zfi
VA
m
V?A
%
Bild 3:
Zwischenstadium der
N
Entfaltung
Wi
v-ioo
5^
ry,
^
ss
Bild 4:
\
c?
k?1*^»
Die vollständig
entfaltete Struktur
V-101
Es ist
Methode
zu
beachten, dass die Gebilde, die durch die vorher geschilderte
zur
Bildung
von
Raumfachwerken mit
grosse Unterschiede in der
vermeiden, Ausschnitte
es
trapezoidalem
Raster
entstehen,
Länge ihrer Stäbe aufweisen. Deshalb sollte
zu
man
wählen, in denen einer der Pole der eingeteilten
legen
Es ist
zu
empfehlen, eine grosse Anzahl Meridianebenen
jene Ausschnitte
zu
bevorzugen, die im Gebiet der Aequatorebene liegen,
Sphäre liegt.
und
wenn
möglich sogar eine Symmetrieebene im Aequator haben.
\
z Z
z
z
z /
y\\
z
z
zu
V-102
\
V
V-103
PYRAMIDALE ODER PSEUDOPYRAMIDALE GRUNDELEMENTE MIT RHOMBOIDALER BASIS
analog
Man kann hier
d.h. bei einer
dingungen
Fall der
zum
Pyramide mit trapezoidaler Basis vorgehen,
gegebenen Basis kann
durch
man
Anwendung der Faltbarkeitsbe-
der einzelnen Stabketten sowie durch weitere
dingungen,
die sich
geometrischen
der
aus
Form des
geometrische
Be¬
jeweiligen Gebildes
ab¬
leiten
lassen, die Lage der Pyramidenspitze ermitteln, so dass das Gebilde
gefaltet werden kann. (Vergl. Abschnitt "Pyramidales Grundelement mit tra-.
pezoidaler Basis")
Wir werden
uns
die durch eine
hier auf die
Anordnung
Elementen als Ganzes
1.
Erläuterung
faltbaren
von
einzelnen Gebilden
von
pyramidalen oder pseudopyramidalen
gefaltet werden können.
Zweiläufige Stabrostkuppel
beschränken,
V-104
2.
Zylindrisches Fachwerk
VI Anhang
VI-1
Weitere Lösungen
zum
Problem der Faltung
von
Raumfachwerken
Prinzipien der Faltbarkeit im Raum gehen aus von
einzelnen faltbaren Grundelementen, die durch Aneinanderreihen in einem geo¬
Die bisher beschriebenen
metrischen Rasternetz ein Gebilde
Wir haben diese
ergeben,
das seinerseits auch faltbar ist.
Prinzipien geometrisch und kinematisch untersucht und durch
Beispiele belegt.
Es wird hier
versucht, anhand zweier Beispiele
Problems der
Faltung
von
Raumfachwerken
zu
neue
Methoden
zur
Lösung des
erläutern, indem wir in einem
Beispiel apriorisch von einem Fachwerk ausgehen und versuchen, dieses
durch kontrollierte Auflösung von Bindungen so zu verändern, dass es gefaltet
ersten
Beispiel wird die Faltbarkeit durch eine zweckmässige
Ausbildung der Stäbe und Knoten erreicht, d.h. indem man Dreh- und Schiebegewerden kann. Im zweiten
lenke einführt.
Nehmen wir ein
aus
halben Oktaedern
gebildetes
im Bereich der räumlichen Fachwerke sehr oft
/
\
\
Fachwerk. Dieser
vor.
\
\
Typ kommt
VI-2
Frage, wie das Gebilde gefaltet werden kann, d.h. wie
Es stellt sich die
Ausbildung
die
der Strukturteile
(Knoten und Stäbe) angepasst und welche
Bindungen aufgelöst werden müssen,
ein labiles Gebilde
mittels einer
zu
dem starren räumlichen Fachwerk
um aus
machen, das dadurch, dass die relative Lage der Stäbe
geordneten Bewegung
wird, grössere Umwandlungen des
verändert
Volumens sowie der Gesamtfläche der Struktur erlaubt.
Beispiel
1:
Betrachten wir ein Fachwerk wie auf der
vorangehenden Seite abgebildet.
Obergurt-, 16 Untergurt-
Es besteht aus 12
und 32
die durch
Diagonalstäben,
21 Knoten miteinander verbunden sind.
Dies
ergibt:
F
=
F
=
3g
-
3*21
n
-
-
6
(12 +16+32)
Die Struktur ist starr;
es
-
6
=
-3
resultieren drei
überzählige Bindungen.
Prinzip der Faltbarkeit:
Betrachten wir einen
Verbindungsknoten
u
VI-3
Dieser
Verbindungs¬
knoten kann
so ausge¬
bildet werden, dass die
Diagonalstäbe von den
Obergurt- bzw. Unter¬
gurtstäben getrennt
u
werden.
^
Die Knoten werden im Ober- und
Untergurt in beiden Richtungen alternierend
angeordnet.
© Doppelte Knote
•
•C
*)r
i
c
K£r
Imi
Einfache Knote
-^1
UNTERGURT
OBEROURT
VI-4
Durch die
wie
folgt:
g
=
31
=
60
n
F
=
3g
F
=
3-31
F
=
27
-
Zweiteilung
n
-
-
60
der Knoten verändert sich der
gesamte Freiheitsgrad
1
-
6
gesamte Gebilde ist labil und lässt sich durch eine geordnete gegen¬
seitige Bewegung der Strukturteile zusammenfalten. Das heisst, alle Stäbe
kommen parallel zu einer Achse senkrecht zur Ebene der Struktur zu liegen.
Das
VI-5
Die
folgende Photoserie zeigt drei verschiedene Phasen
beschriebenen Struktur
am
der
Faltung der
Modell:
Bild 1:
K
^
«
1
^
/ä
^
Das Modell von der
Seite gesehen
WA
Bild 2.-
Vi
Dadurch, dass wir die
1
M
einzelnen Knoten zwei¬
teilen, die die Diagonal¬
&
&
stäbe mit den Ober¬
bzw. Untergurtstäben
verbinden, verwandelt
sich die starre Struktur
in einen labilen Mecha¬
nismus, der gefaltet
werden kann.
Bild 3?
Bei der gefalteten
Struktur sind alle Stäbe
quasi parallel
Achse
um
gruppiert.
eine
VI-6
Beispiel
2:
/
s
\
\
\
Prinzip der Faltbarkeit
Die
Faltung kommt dadurch zustande, dass die Bindungen der Stäbe AC und AE
im Knoten A gelöst werden, währenddem die Kanten AB und AD in A durch ein
Drehgelenk verbunden bleiben. Die Stäbe AC und AE können sich nun ihrer Länge
nach durch den Knoten A verschieben. Man beachte, dass sich während des Falt¬
vorgangs die ursprünglich quadratische Basis der Pyramide in einen Rhombus
und schliesslich in eine Strecke verwandelt, wobei der Punkt A in die Ebene TT
zu liegen kommt.
'>
VI-7
\J
•A
R
\>
/
/
An das
so
entstandene Grundelement kann das
folgende kinematische Schema
assoziiert werden:
f=l
n
gl
g2
g^
=
10
=
2
=
4
=
1
f=1
=
f=1
C f=1
F
=
3 (n-l)
F
=
3
F
=
2
-
(g±
2 (2
(10-1)
27
2 (13)
1
-
-
+
+
2g2 + 3g3)
2-4
+
3-1)
=
Der Mechanismus ist
zwangsläufig.
VI-8
folgende Photoserie zeigt verschiedene Stadien der Entfaltung in der
Aufsicht sowie Details der Knoten, die die Entfaltung ermöglichen:
Die
m
m*
?T<
sim
a
Bild 1:
.Die voll entfaltete
Struktur
m
Bild 2:
Zwischenstadium der
Faltung
¦B
3
ä
^
Bild 3
H
H
s
VI-9
Bild 4:
pt
Das zusammengefaltete
Modell
1
U
Bild 5:
Ti
Aufsicht auf einen
Knoten
ATi
VA
nPSffP
Bild 6:
Seitensicht der Knoten
*
vr-io
Bild 7:
Detailansicht eines
A
Knotens
A
<•
Zusammenfassung
vorliegende Arbeit stellt geometrische Prinzipien dar, deren Anwendung auf
Strukturen aus Stäben und Knoten faltbare Grundelemente ergeben. Das Anordnen
Die
dieser Grundelemente in ebenen oder räumlichen Rastern führt
über ihre
sie
primäre Funktion als Tragstrukturerihinaus
gefaltet
so
zu
Fachwerken, die
ausgebildet sind, dass
werden können.
Kapitel gegliedert, wobei Kapitel I als Einführung und
Kapitel II als kurze Zusammenfassung wichtiger Begriffe dienen. Im Kapitel III
wird mit der Beschreibung der Faltbarkeitsprinzipien begonnen, indem von einem
rhombischen Grundelement, das aus Stäben und Knoten besteht, ausgegangen wird.
Faltbare Fachwerke können durch Anordnung solcher Grundelemente in ebenen Rastern
gebildet werden. Diese werden nach geometrischen und kinematischen Aspekten
(Freiheitsgrade) untersucht und mit einer Reihe Beispiele belegt. Die für ebene
Fachwerke definierten Prinzipien werden mit Hilfe rhombischer 'Modularer Grund¬
elemente1 für die Faltbarkeit im Raum auf die Faltung räumlich planparalleler
Fachwerke übertragen. Danach folgt in Kapitel VI die Betrachtung der Faltbar¬
keit anhand von Polyedern, an welche ein Gebilde aus gelenkig miteinander ver¬
bundener Stäbe assoziiert wird, so dass faltbare Grundelemente entstehen, die
in ebenen oder räumlichen Rastern aneinandergereiht faltbare Fachwerke ergeben.
Die Arbeit ist in sechs
Polyeder wird der Oktaeder untersucht. Die dabei gewonnenen Prinzipien
ergänzen die im Kapitel III erläuterten Prinzipien.zur.Faltung räumlicher
planparalleler Fachwerke. Als nächster Polyeder wird der Würfel studiert. Aus
den dabei gewonnenen Prinzipien der Faltbarkeit lassen sich Grundelemente ab¬
leiten, die nicht nur die Faltung ebener und planparalleler Raumfachwerke er¬
lauben, sondern den Uebergang zur Bildung weiterer Grundelemente zur Faltung
Als erster
sphärischer
Kapitel
und
zylindrischer Raumfachwerke darstellen.
sphärischen
V behandelt insbesondere die
Fachwerke. Nach einer kurzen
Einführung in die geometrischen Eigenschaften sphärischer Polyeder werden Bei¬
spiele verschiedener faltbarer Fachwerks-Typen beschrieben, die durch Aneinander¬
reihen der vorher definierten 'Modularen Grundelemente'
Kapitel
VI
zeigt zwei Varianten
zur
werden können.
Faltung räumlicher planpäralleler Fachwerke
aus
halboktaedrischen Elementen. Es wird eine Reihe
sen
die
kann.
gebildet
Beispiele gezeigt,
vielfältigen Möglichkeiten faltbare Strukturen
zu
bilden
nur
die indes-*
andeuten
Summary
geometrical principles which, when applied to structures
made of bars and nodal connections, can form folding basic elements. The
arrangement of these basic elements in planar or spatial girds gives rise
This thesis describes
to stable trussed
bearing
structures which
can
also be folded.
chapters. Chapter I serves as an introduction
and chapter II as a short summary of important definitions. Chapter II begins with the description of the principles of folding pertaining to basic
rhombic elements made of bars and notal connections. Folding trusses are
formed by joining these elements in planar girds. These are there examined
for their geometric and kinetic aspects (i.e. degrees of freedom), and are
The thesis is devided into six
illustrated with
to
ränge of
examples.
The
principles
folding defind for
of
applied with the aid of modular basic rhombic elements
derive principles of three-dimensional folding. These are then applied
spatial, trussed structures.
planar frames
to
a
are
folding qualities of polyhedrons, applied to figures
made of bars and articulated joints, creating folding basic elements which,
joined together in planar and three-dimensional girds, make up folding trusses.
IV studies the
Chapter
polyhedron examined is the octahedron. The principles thus defined
complete those principles explained in chapter III for the folding of space
frames. The next polyhedron studied is the cube. From the principles of fold¬
The first
ing
deduced, basic elements can be defined which lead to further ele¬
capable of generating folding spherical and cylindrical spatial trusses.
thus
ments
Chapter
particularly with spherical trusses. After a Short introduc¬
geometrical characteristics of spherical polyhedrons, examples
V deals
tion to the
of various
the
types of folding
previously
trusses
are
described, which
can
be formed
using
defined modular basic elements.
folding three-dimensional trusses made
of semi-octahedral elements. The examples given can only begin to suggest
the numerous possibilities available for making folding structures.
Chapter
VI shows two variations for
Literatur
(Societe Nationale de 1'Industrie Aerospatial)
Centrifugal regulator for control deployement rates of deployable
AEROSPATIAL
elements.
Aerospatial,
S.N.I.
Paris 1980
Engineering Laboratory
Aero-Mechanical
Command,
Expandable shelter
Airtransportable shelter
-
US
Army, Research and Development
Containers
Massachusetts, USA, 1978
ALASIC C:
Geometria
U.
Trigometria
e
Hoepli editore,
de la sfera-;
Milano 1900
BRINK N.O.:
Research
on an
expandable
Nasa contractor
Washington D.C,
airlock
utilizing
the elastic recovery
principle.
Nasa CR-351
report,
1965
N.O., Andersson B.C., Thompson C.E., Wolcott C.E.:
BRINK
Development
concept for expandable
and evaluation of the elastic recovery
space structüres.
Nasa contractor
Washington D.C,
report CR-121
1964
D., Graefe R., Hennicke J., Kugel F., Pankoke W., Otto F., Schock H.J.,
BLUEMEL
Wagner
J.:
Wandelbare Dächer.
Flächentragwerke (IL)
Institut für leichte
Universität
BEYER R.:
Technische Raumkinematik
Springer Verlag Berlin 1963
BEYER R.:
Zur
Synthese
ebener und räumlicher Kurbeltriebe.
VDI-Verlag GmbH, Berlin 1939
BEYER R.:
Technische Kinematik.
Verlag
von
Johann A.
Barth, Leipzig, 1931
BEYER R.:
Kinematik, Bewegungsgeometrie für Ingenieure.
Dr. Max
Jänecke, Verlagsbuchhandlung, Leipzig, 1928
Stuttgart, 1972
BUCKMINSTER FÜLLER R.:
•Synergetics, Exploration in the Geometry of thinking
Publishing Co.,
Macmillan
New
York, 1975.
BLOCH S. Seh.:
Angenäherte Synthese von Mechanismen.
Verlag Technik Berlin, 1951
BORREGO John:
Space grid
structures skelatal frameworks and stressed-skin
Massachusetts Institut of
1968.
Technology (M.I.T.),
MIT press,
Systems.
Cambridge, Mass.,
CRITCHLOW Keith:
Order in
a design source book.
Space
Thames and Hudson, London, 1976.
-
NASA:
Nasa contractor
report CR-1735
Nasa, Washington D.C, 1971
COXETER H.S.M.:
Unvergängliche Geometrie.
Birkhäuser Verlag Basel und Stuttgart,
1963.
DIJKSAMAN E.G.:
Motion
Geometry of Mechanisms
Verlag Technik Berlin, 1951.
DAVIS J.M.:
Space
Space
structures.
Internat. Conference of
Blackwell Scientific
structures, 1966.
Publication, Oxford, 1967.
EMERICH D.:
Exercices de Geometrie construetive.
Travaux d'etudiats. Seminaire et laboratoire de recherche structural.
Ecole Nationale Superieure des Beaux Arts, Paris, 1970
ENGEL H.:
Systeme.
Deutsche
Verlags GmbH, Stuttgart,
1967.
FAIRCHILD H.:
deployable
Positive
Nasa Contractor
solar array
Report
No Nas
development program.
5-3988, 1964
FUCKE R.:
Darstellende Geometrie.
Verlag
Harri
Deutsch, Zürich, 1975
GREENE W.:
Designing Procedure for a Tension-wire stiffened Truss-Colomn.
Nasa Contractor Report 3273, 1980
A
GARNISCH R.:
Aesthetik, Konstruktion und Design.
Strukturale Aesthetik.
Otto Meier
Verlag, Ravensburg,
1976
A., Dragomir V.:
GHEORGIU
Geometry of structural forms.
Applied Science Publishers Ltd., London, 1978
Corporation:
HARRIS
Large deployable antenna development program.
Nasa contractor
HUG B.,
report CR-2894, Melbourne, 1977
Fuessinger
R.:
Entwicklung einer transportablen Festbrücke in Verbundbauweise
Alu und Kohlenstoff-faserverstärktem Kunststoff.
Schrifttum Bauwesen,
HARRY
L., Morgan Jr.
aus
Zürich, 1980
u.a.:
Aerodynamic and deployement characteristics of multistage canopy and
suspension-line reefing Systems for a twin-keel all-flexible parawing.
Nasa technical note, Nasa TND-6306, Washington D.C, 1971
HEDGPETH J.M.:
Survey of future requirements for large space structures.
Nasa contractor
HENRICI
report CR-2621, Washington D.C, 1976
P., Huber A.:
Analysis II
Verlag der Fachvereine
an
der ETH Zürich, 1973
HUNT K.H.:
Geometry of Mechanisms
Claredon press, Oxford, 1978
Kinematic
HJERSMAN P.:
Dome notes
Berkeley University press, Berkeley, 1975
HILBERT
D., CONN-VOSSEN S.:
Geometry and the Imagination
Chelsea Publishing Company, New York, 1952
HAECKEL E.:
Kunstformen der Natur
Bibliographisches
Institut
Leipzig,
1899
ISSAM ELDIM ABDON BADR:
Vom Gewölbe
zum
räumlichen
Tragwerk.
3275, 1962
ETH Zürich Dissertation Nr.
Flächentragwerke
Institut für leichte
der Universität
Stuttgart:
10 Jahre IL, 1964-1974
Selbstverlag Stuttgart, 1975
KENNER H.:
Geodesic math and how to
University
of
use
it
California, Berkeley, Press,
Los
Angeles, London,
1976
KRAUS R.:
Getriebelehre
VEB
Verlag Technik, Berlin,
1954
KUENZLE O.:
Aspekte der Optimierung beim Entwurf von Raumfachwerken
ETH Zürich, Dissertation Nr. 5662, 1976
KENNER P.M., Churchill
Geometrie
aus
Stahl
T.T., Holt R.:
Aerodynamic and Kinematic characteristics of
during deployement
Nasa contractor report CR-1788, Washington D.C, 1971
two twin
parawings
LE RICOLAIS R.:
Structures
implicit
and
explicit
Revue of the Graduate School of Fine
Falcon Press,
Philadelphia,
LEKTIN A., Rivaud
J.:
Algebra Moderna
Aquilar, Madrid, 1961
1973
Arts, Univ. of Pennsylvania.
^^
LUDEWIG S.:
Montagebau
Verlag Rudolf Müller, Köln,
1972
LALVANI, H.:
Transpolyhedra
Papers in theoretical morphology I, published by
H.
Lalvani,
New
LIEB P.:
Analytische Geometrie der Ebene.
Georg
Verlag, Braunschweig,
Westermann
1963
LICHTENHELD, W.:
Konstruktionslehre der Getriebe.
Akademie-Verlag, Berlin,
1970
MAKOWSKI Z.S.:
Structures
spatiales.
Cahiers du Centre d'Etudes Architecturales (14)
,
Paris, 1972
MARKOWSKI, Z.S.:
Räumliche
Tragwerke aus Stahl.
Verlag Stahleisen GmbH, Düsseldorf, 1963
MERIAN J.L.:
Dinamica.
Reverte
Barcelona, 1972
MENGERINGHAUSEN M.:
Raumfachwerke
aus
Stäben und Knoten.
Komposition im Raum, Band I,
Bauverlag GmbH, Wiesbaden und Berlin, 1975
MITTAG, M.:
Baukonstruktionslehre.
Bertelsmann
NICKEL
Verlag, Gütersloh, 1952
H., Kettwig G.,
u.a.:
Analisis, Algebra und Geometrie für Ingenieure, Band I, Band
Verlag Harri Deutsch, Thun und Frankfurt a.M., 1978
NASA:
SUNFLOWER, Study of advanced precision deployable antenna
Nasa contractor
report, CR-162631, Washington D.C, 1979
II
York, 1977
NASA:
Deployable
Nasa
Flexible Tunnel
MFS-22636, Washington D.C, 1975
No.
case
NATIONAL TECHNICAL INFORMATION
Air-mobility rigid
Airforce
Systems.
shelter
Engineering Center, PB-251 753, Washington, 1975
Development
NATIC
SERVICE, US DEPT. OF COMMERCE:
Center:
Relocable Maintenance Hanger
Cöncept Evaluations
01760, Natic, Massachusetts, 1975
Natic
ONTEGA-PEREZ M.A.:
Systems Study
Foldable Boom
Instituto Nacional de Tecnica Aerospacial,
1130/70, 1973
Madrid, Spain
ESRO contract No
OTTO
F., Helmecke J.G.:
Lebende und technische Konstruktionen.
Deutsche
Bauzeitung, Heft 11, 1962
OTTO F.:
Spannweiten
-
Ideen und Versuche
Leichtbau.
zum
Verlag Ullstein Berlin, Frankfurt a.M., 1965
OTTO F.:
Gitterschalen.
Veröffentlichungen des Institutes für Flächentragwerke der Universität
Stuttgart, 1974
OTTO F.:
Form und Konstruktion.
Verlag Gerd Hatje, Stuttgart, 1976
PACIFIC DOMES:
Dome Book 2
Architectural
London, 1971
Design (distribution)
PETERS, T.F.:
Time is Money
Die Entwicklung des modernen Bauwesens
Verlag Hofman, Stuttgart,
1981
PRENIS J.:
The dorne builders handbook
Running Press, Philadelphia, 1973
POLYA G.:
Introduction and Analogy in Mathematics, Princeton Univ. Press, Princeton, N.J.
1954
PEARCE S. und P.:
Polyedra Primer
van
Mostrand Reinhold
Company,
New
York, London, 1978
PUGH, A.:
An Introduction to
Tensegrity
University of California, Press, Berkeley,
Los
Angeles, London,
1976
PUGH, A.:
a Visual approach
Polyedra
University of California, Press, Berkeley, Calif. 1976
-
REUTTER F.:
Darstellende
Verlag
II
Braun, Karlsruhe, 1974
G.
RUEHLE, H.
u.a.:
Konstruktion und Ausführung, Band 2
Dachtragwerke
Müller, Köln 1970
Räumliche
Verlag
Geometrie, Band I, Band
R.
-
SYMPOSIUM über Leichtmetallkonstruktionen
der Int. Vereinigung für Brückenbau und Hochbau,
Referatsammlung
IVBH, Zürich, 1975
SUGO J.:
Hardwall
expandable shelter
Civil and environmental Engineering Development Office, Washington, 1977
SCHUERCH H.,
Large
Low
Hedgepeth
J.M.:
Frequency Orbiting Radio Telescope
-
Nasa contractor
report RC-1201, Washington D.C, 1968
H., Robbins W.:
SCHUERCH
Rotary deployable space solar power supply
Nasa contractor report CR-122, Washington D.C, 1962
SCHUERCH H., Preiswenk
P., Hedgepeth J.:
Axisymmetric and cylindrical isostabiloids
Nasa contractor report CR-1444, Washington D.C, 1969
SCHUERCH
H., Mac Neal R., Hedgepeth J.:
Heliogyro
Solar Sailer
Nasa contractor
Summary Report
report CR-1329, Washington D.C, 1969
STIEFEL, E.:
Lehrbuch der Darstellenden Geometrie
Birkhäuser
Verlag Basel und Stuttgart, 1971
¦¦*¦
STUESSI F.:
Baustatik I
Verlag
Birkhäuser
Basel und
Stuttgart, 1962
SCHATZ P.:
Rhythmusforschung und Technik
Verlag Freies Geistesleben, Stuttgart, 1975
Surrey University, Ghilford, England:
Report of the second Conference on Space Structures, 1975
A., Koptsik V.:
SCHUBNIKOV
Symmetry in Science and
Art
Plenum press, New York,
London, 1974
SIEGEL C.:
Strukturformen der modernen Architektur
Verlag Gallwey, München, 1970
SPEISER A.:
Die Theorie der
Gruppen von endlicher Ordnung
Verlag Julius Springer, Berlin, 1937
SPIEKER H.:
Baugeometrie 1,
Modul
Baugestaltung ETHZ,
Schriftenreihe
1975
TORROJA E.:
Razön y
ser
de los
tipos estructurales
Ed. Artes Gräficos SA, Madrid, 1960
TUERKCUE H.:
Beitrag
mit
T.U.
zur
Geometrie der
Berücksichtigung
von
Montage
-
Kugelkuppeln
konstruktiven Kriterien
Berlin, 1973
VOLMER J.:
Getriebetechnik
VEB
Verlag Technik, Berlin,
1972
WASMUTHS
Lexikon der Baukunst
Ernst Wasmuth
AG, Verlag Berlin, 1930
WUCINS WONG:
Principles
van
of three-dimensional
Abstrand Reinhold
Company,
design
New
York, 1977
WACHSMANN, K.:
Wendepunkt im
Bauen
Krausskopf Verlag Wiesbaden, 1959
WEIZENBOECK R.:
Der vierdimensionale Raum
Birkhäuser
Verlag
Basel und
Stuttgart, 1956
Verlag
Basel und
Stuttgart, 1955
WEYL H.:
Symmetrie
Birkhäuser
ZIEGLER, H.: MECHANIK, Band I und Band II, Birkhäuser Verlag Basel
1960
u.
Stuttgart,
ZEITSCHRIFTEN
PARAMETRO
Mensile internazionale di architettura urbanistica,
Faenza editrice Italia No 80, 1979
Musmeci S.
Sergio Musmeci o delle Tensione cognite
ZODIAC
19, 1969
Review of contemporary architecture
Edizioni di communitä Milano
Füller R.B., Neumann
u.
Hecker, Griswold, Kuhn W., Steher
J.
ZODIAC
21, 1971
Tensile space
pneumatic
structures
ZODIAC
22, 1971
Light
structures
Le Ricolais
u.a.
L'ARCHITECTUR D'AUJOURD'HUI
-Nr.
-
-
-
-
Nr.
Nr.
Nr.
Nr.
99, 1961 (Buckminster Füller)
108, 1963 (3o ans de recherches
128, 1966 (Le Ricolais R.)
141, 1969 (Geometrie materiaux,
160, 1972 (Le Ricolais R.)
sur
E.
les structures, Le Ricolais R.)
Pinero)
Lebenslauf
Name
Calatrava Valls
Vorname
Santiago
geboren
28.7.1951 in Benimamet
Zivilstand
verheiratet, 1 Kind
1957
Volksschule und
-
1968
(Valencia) Spanien
Gymnasium
in
Valencia, Abschluss mit
Maturität
1968
-
1969
Besuch der Kunstschule "Escuela de Artes y Oficios Artisticos
de Valencia
1969
-
1974
Architekturstudium
an
Superior de
der Escuela Tecnica
Arquitectura de Valencia, Abschluss mit Diplom
1974
1975
-
-
Vertiefungsrichtung Urbanistik an
der Escuela Tecnica Superior de Arquitectura de Valencia,
Abschluss mit Diplom
1975
Nachstudium in der
1979
Studium
Abt.
Eidgenössischen Technischen Hochschule Zürich,
Bauingenieurwesen, Abschluss mit Diplom.
an
der
Gleichzeitig Erarbeitung
der Dissertation über
zusammenfaltbare Fachwerke.
1978
-
1979
-
1981
-
1979
Assistent
am
Lehrstuhl für Konstruktion
1981
Assistent
am
Institut" für Hochbautechnik
Assistent
am
Institut für
an
der
Eidgenössischen
Flugzeugstatik
und Leichthau
Technischen Hochschule Zürich.