knoten falls

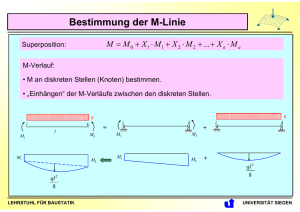
Bildungsgesetze
1. Bildungsgesetz:
Von einem Grunddreieck mit 3 Stäben ausgehend wird ein neuer
Knoten durch 2 neue Stäbe, die nicht auf einer Geraden liegen,
angeschlossen.
Es gilt:
2k = s + 3
Grunddreieck
LEHRSTUHL FÜR BAUSTATIK
UNIVERSITÄT SIEGEN
Bildungsgesetze
2. Bildungsgesetz:
Zwei nach dem 1. Bildungsgesetz aufgebaute Fachwerke werden verbunden durch
1) 3 Stäbe, die nicht parallel sind und sich nicht in einem Punkt schneiden; oder
2) einen Stab und ein gemeinsamen Knoten der beiden Teilfachwerke; oder
3) einen gemeinsamen Knoten und eine zusätzliche Lagerung (Festhaltung).
F1
Gemeinsamer Knoten
F2
F2
F2
1)
F1
F1
2)
3)
Zusätzl. Festhaltung
LEHRSTUHL FÜR BAUSTATIK
UNIVERSITÄT SIEGEN
Bildungsgesetze
3. Bildungsgesetz:
In einem Fachwerk nach dem 1. oder 2. Bildungsgesetz wird ein
Stab umgebaut. Der umgebaute Stab ist an einer anderen Stelle
so einzufügen, das das neue Fachwerk kinematisch bestimmt wird.
LEHRSTUHL FÜR BAUSTATIK
UNIVERSITÄT SIEGEN
Bestimmung der Stabkräfte
Allgemeine Bemerkungen:
1) Vor de Bestimmung der Stabkräfte ist es zweckmäßig, zuerst die
Auflagerreaktionen zu bestimmen. Dies erfolgt aus den 3 Gleichgewichtsbedingungen am Gesamtsystem.
2) Außerdem ist es zweckmäßig, Nullstäbe vorab zu finden, um die
Anzahl der Unbekannten zu reduzieren.
Verfahren zur Bestimmung der Stabkräfte:
1) Knotenpunktverfahren
2) Rittersches Schnittverfahren
3) Cremona-Plan (grafisches Verfahren)
LEHRSTUHL FÜR BAUSTATIK
UNIVERSITÄT SIEGEN
Nullstäbe
S1
Regeln zum Auffinden der Nullstäbe
1) 2 Stäbe an einem unbelasteten Knoten
mit unterschiedlichen Richtungen sind
Nullstäbe.
2) 2 Stäbe an einem belasteten Knoten:
Greift die äußere Kraft in Richtung eines
Stabs an, so ist der andere Stab ein
Nullstab.
3) 3 Stäbe an einem unbelasteten
Knoten: Falls 2 Stäbe davon in gleicher
Richtung liegen, dann ist der dritte Stab
ein Nullstab.
LEHRSTUHL FÜR BAUSTATIK
S2
1)
S1 = 0, S 2 = 0
S1
2)
S2
S1 = F , S 2 = 0
S1
3)
S2
S3
S1 = S 2 , S 3 = 0
UNIVERSITÄT SIEGEN