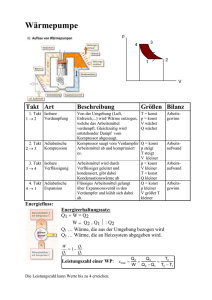
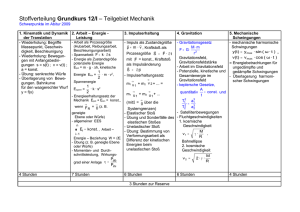
F p fl AF = F p È AF = F + p fl A p È = RT

Systeme
Systemgrenze
Bei jeder Bilanzierung:
1.
Bilanzgebiet abgrenzen durch Wahl der
Systemgrenze
Massenbilanz; Bilanzierung der Massenströme
Energiebilanz; Bilanzierung der Energieströme
2.
3.
1
! m ! w2
2
[kJ/s]
[kg/s]
EIN - AUS = zeitliche Veränderung im Bilanzgebiet
•
•
•
•
HK• + HL• + HW• − HRG
− HS• − HD• − Eelektr
− Qstr
− QVerlust
=
Qi* [kW]
beliebig
beliebig
=0
#0
=0
Beispiel
Fön
Kühlschrank, Pneu
Thermoskanne
Pfanne, Radiator
gibts kaum
Konvention:
Dem System zugeführt = positiv
vom System abgeführt = negativ
Beispiel KVA:
d
Kehricht + Luft + Wasser - Rauchgas - Schlacke - Dampf =
Bilanzgebiet
dt
dm
•
mK• + mL• + mW• − mRG
− mS• − mD• =
Stoffüsse
dt Bilanzgebiet
dE
dt Bilanzgebiet
Energieüsse
Wi* [kW]
beliebig
beliebig
beliebig
beliebig
=0
stationär: zugeführt = abgeführt (d/dt = 0)
instationär: zugeführt # abgeführt (d/dt # 0)
Systembezeichnungen:
mi* [kg/s]
#0
=0
beliebig
beliebig
=0
T!
g!
H!
R!
v!
n!
M!
!!
E
E+H
prozentualer
Anteil Energie
(kin, pot) zur
Gesamtenergie
mi
! Vtot
mtot
Thermo- / Fluiddynamik
Zustandsgrössen
V! =
T in °K
T!
# V"
T
"
Aufheizfvorgang:
p=konst., m=konst.
p" M
z" #" T
f
! R!T
2
f=3
f=5
f=5
Kapitel 1
Systeme, Zustandsgrössen
u, h sind
druckunabhängig.
H und U sind aber
druckabhängig.
Oszillationen (Schwingungen der
Moleküle) zählen bei den
Freiheitsgraden doppelt!
&
#f
h = u + p ! " = % + 1( ! R ! T
$2 '
1-atomig!
2-atomig!
mehr-atomig!
kalorische (h, u)
u=
Helium!
Sauerstoff!
Luft!
cp-Wert in
Tabellen
cv-Wert in
Tabellen
Achtung: Bei verschiedenen Temperaturen
können die Moleküle auch höhere
Freiheitsgrade besitzen (stärkere
Oszillationen).
Enthalpie
bei idealem Gas z =1
bei realem Gas siehe Bohl S. 453
!=
R~ = 8314.51 J/kmol · °K
R~ = 8.31451 J/mol · °K
1 mol = 6.02 * 1023 Teilchen
1 kmol = 6.02 * 1026 Teilchen
RLuft = 287 J/kg°K
p ! V = m ! R !T
thermische (p, v, T)
ideale Gasgleichung mit spez. Gaskonstante R
p ! " = R !T
universelle Gaskonstante
!= M"R
p!V = n ! "! T
reale Gasgleichung
W =J/s
[J/kg]
0°C = 273.15°K
[-]
[kJ/kg°K] (V = konst.) (Tab.16)
[kJ/kg°K] (p = konst.) (Tab. 16)
[J/kg]
[J]
[J]
mi
Druck p
!U tot -- Temperatur
T
mtot
massenunabhängig (intensiv)
Stickstoff
Ammoniak
Sauerstoff
z(p,T) = Realgasfaktor
(mit Berücksichtigung externer Einüsse)
N2!
NH3!
O2!
Ui =
spezische Zustandsgrössen
massenabhängig (extensiv)
Vi =
spez. innere Energie!
angereg. Freiheitsgr.!
spezif. Wärmekapaz.!
spezif. Wärmekapaz!
Enthalpie!
innere Energie!
Energie!
mi
! H tot
mtot
u!
f!
cv!
cp!
h!
U!
E!
Hi =
[°K]
[m/s2]
[J]
[J/kg°K]
[m3/kg]
[mol]
[g/mol]
[J/mol °K]
+++ © 2007 by René Sigrist +++ V1.0 +++ Fehler bitte melden an: [email protected] +++ Tabellenangaben beziehen sich auf: Taschenbuch der Physik, ISBN 3-446-22883-7 +++
Temperatur!
Erdbeschl. (9.81)!
Enthalpiestrom!
spez. Gaskonst. (Tab.14)!
spezisches Volumen!
Anzahl Mole!
Molmasse!
universelle Gaskonst.!
E pot = m ! g ! "z
Ekin =
abgeleitete Zustandsgrössen
(nicht direkt messbar)
Beschreibung
Beispiel
einheitliche Zusammensetzung und Rauchgas im Kamin
Phase
räumlich unterscheidbare
Kondensattropfen in Luft
Zusammensetzung und/ oder
Phase
Systembezeichnung
offen
geschlossen
adiabat ($ klein)
diabat/diatherm ($ gross)
abgeschlossen
System
homogenes
System
heterogenes
System
Zustandsgrössen
[N/mm2]
[kg/m3]
[m3]
[kg]
[N]
[N]
[N]
[N]
natürliche Zustandsgrössen
(direkt messbar)
F = p! A
i
Fa = !Fi = ! p " A
Druck!
Dichte!
Volumen!
Masse!
Stangenkraft!
Umgebungskraft!
Kraft ausserhalb!
Kraft innen!
Fa = FSta + pu ! A
p!
"!
V!
m!
FSta!
Fu!
Fa!
Fi!
Druck!
spez. Volumen!
Volumen!
Masse!
Auftriebskraft!
Wärmemenge!
Temperatur!
p-V-T-Diagramm
p!
"!
V!
m!
FA!
Q!
T!
Druck
Volume
n
[N/mm2]
[m3/kg]
[m3]
[kg]
[N]
[J]
[°K]
g!
cv!
cp!
U!
A!
d!
b!
r
tu
ra
pe
m
Te
Auftrieb
T
V
tot
Bei Gasen:
c = cv wenn V = konst.
c = cp wenn p = konst.
i
!y
i
yi =
=1
ni
i
=
"!
i
=1
y1
z
y2
p
V
y=
w
z
z
! x + y2 " x2 !
w
w
x1
p = konst.
T
Isobare
V
wi =
mi
ni " M i
i
=
yi " Mi
MGemisch = " y i ! M i
Molmasse im Gasgemisch
Isotherm
=
i
i
i
! m ! (n " M ) ! ( y " M )
i
Massenteile in Molteile
wi: 20% = 0.2
RGemisch = " w i ! Ri
Gaskonstante im Gasgemisch
wi
Mi
mtot
mGemisch
wi
Mi
n tot =
Einheiten in Diagrammen:
!!
°C
"!
kg/m3
h!
kJ/kg
s!
kJ/kg°K
cp,cv! kJ/kg°K
Kapitel 1
p-V-T-Diagramm, Auftrieb, Volumen, Wärmeenergie
x2
Isobar
mi
Mi
n i = y i ! n tot
mi
Mi
! n !( ) !( )
=
m !R
!T
p = tot Gemisch
Vtot
V = konst.
Isochore
Gasgleichung
i
Massenteile in Molteile
p !V = n ! "! T
tot
m
!m
i
Massenanteil wi
i
i
Anteile im Gas
p
p
Isochor
Wärmeenergie
Thermo- / Fluiddynamik
Flächen/Volumen
Kreis
Zylinder
Pyramide
Kugel
Kegel
wi =
n
!n
i
Molanteil yi
yi =
i
"V
Vi
Volumenanteil #i
!i =
=1
Molanteil yi = Volumenanteil #i
i
[m2]
[m2]
[%]
[%]
[%]
!w
Oberäche!
Manteläche!
Molanteil (80% = 0.8)!
Massenanteil (80% = 0.8)!
Volumenanteil (80% = 0.8)!
Kreisringäche
AO!
AM!
ni !
wi!
#i !
Hohlzylinder
Erdbeschl. (9.81)!
[m/s2]
spezif. Wärmekapaz.! [kJ/kg°K] (V = konst.) (Tab.16)
spezif. Wärmekapaz! [kJ/kg°K] (p = konst.) (Tab. 16)
Umfang!
[m]
Fläche!
[m2]
Durchmesser!
[m]
Breite!
[m]
+++ © 2007 by René Sigrist +++ V1.0 +++ Fehler bitte melden an: [email protected] +++ Tabellenangaben beziehen sich auf: Taschenbuch der Physik, ISBN 3-446-22883-7 +++
Kontinuitätsgleichung
m = ! " A " w
V = A ! w
m = V! "
wenn p=konst.
1. Hauptsatz für geschlossene Systeme (Energieerhaltungssatz)
1. Hauptsatz für offene Systeme (Energieerhaltungssatz)
Geschwindigkeit!
Rohrreibungszahl!
Rohrlänge!
Rohrdurchmesser!
anger. Freiheitsgrade!
Drucksverlustbeiwert!
Arbeit!
'-(
[m/s]
[-] (Bohl S. 475)
[m]
[m
[-]
[-]
[J]
Einschiebe- und Ausschiebeleistung
w!
%!
L!
d!
f!
&!
W!
6
diabat: T( = T'
adiabat, reibungsfrei: Isentrop
1
2
3
4
5
1: ist im stationären Fall immer 0! (stationär = keine Durchussänderung)
2: Kolbenarbeit (wenn keine Kolben = 0)
3: Wellenarbeit (wenn keine Wellen = 0)
4: Feldenergie/Gravitation (wenn horizontale Röhre = 0)
5: Wärmeströme (wenn adiabat = 0)
6: konvektiver Energieuss (Massenuss vom Eingang bis Ausgang)
[m/s]
[kg/m3]
[W]
[J]
[J]
[-]
[m/s]
Kompression: WSystem > 0
Expansion: WSystem < 0
Leistung von Normalkräften oder Druckkräften
Geschwindigkeit!
Dichte (Tab. 1)!
Pumpleistung!
Pumpenergie!
Verlustenergie!
Wirkungsgrad (<1)!
mittlere Geschwind.!
Einschiebe- und Ausschiebearbeit
w!
"!
Pp!
#ep!
#ev!
$!
w!
Thermo- / Fluiddynamik 1
Anwendung Bernoulli-Gleichung
!p
"
'
0
Aususs aus Gefäss
pU
pU
(
Druckwasserleitung
'
1. Grundgleichung
pU
0
1
3
2
1
'
0
0
8829
8829
9810
epot
[Nm/kg]
100
9296.8
467.8
467.8
100
edruck
[Nm/kg]
9810
613.2
613.2
613.2
0
ekin
[Nm/kg]
0
Kapitel 2
Massen- und Energieerhaltung
0
A' = ...
A1 = A2 = A3
A( = 0.25 · A3
"w = 1000 kg/m3
3. w1 = w2 = w3 (gleicher Querschnitt)
2. Werte bei ( berechnen
z' = 1000 m!
z1 = z2 = 900m!
z3 = z( = 0 m!
pu = 1 bar!
w' = 0 (A' >> A()
p( = pu (Freistrahl) = p'
u' = u(
" = konstant
3
w(
(
Summe pro Zeilen immer 9910!
2
wS = wF
auf horizontaler Ebene
uS = uF
Freistrahl
!e =
Einlauf
Rohr
Armaturen
Düsen
Auslauf
Indizes:
S = Stromröhre
F = Freistrahl
Energieform
!p = " # $2 # w 2 # dL
!p = !e " #
Eindimensionale Bernoulli-Gleichung
w!2 1
w2 1
+ # p! + g # z! + $e p = % + # p% + g # z% + $ev
2 "
2
"
#ev können durch z.B.
Reibung entstehen.
Druckform
! 2
!
" w# + p# + ! " g " z# + $p p = " w%2 + p% + ! " g " z% + $pv
2
2
Höhenform
Pp = m ! "e p
1
p
1
p
! w"2 + " + z" + $H p =
! w%2 + % + z% + $H v
2! g
2! g
#! g
#! g
#
m ! ("ev + "e p )
Pumpleistung
Pp =
)
gerade Rohrstücke
Pumpleistung mit Druckverlust und Wirkungsgrad
"
2
Druckverlust
(
# w2
Druckverluste !p
!p = f
-
[J]
[J/s, W]
[kg/m3]
[J]
[mm] (Bohl S. 478)
[m/s]
[ m /s]
Bei Verlusten:
% = f(Stoff, Rauhigkeit) von 0.01 bis 0.08
(siehe Tafel 30 S. 478 im Bohl)
& aus Bohl S. 180
Formstücke, Armaturen, Ein-, Ausläufe
!p = " # $2 # w 2
3.6
[km /h] =
Diagramm „Sättigungszustand“
v)! gesättigte Flüssigkeit! [m3/kg]
v))! gesättigter Dampf!
[m3/kg]
"))! Dichte Dampf!
[kg/m3]
h)! Enthalpie Flüssigkeit!
[kJ/kg]
h))! Enthalpie Dampf!
[kJ/kg]
r! Verdampfungsenthalpie! [kJ/kg] (h))-h))
) = Flüssigkeit
)) = Dampf
1[ mm Wassersäule] = 9.81[ Pa]
Wärmemenge!
Wärmeuss!
Dichte (Tab. 1)!
Energie!
Rauigkeit!
Leitungsgeschwind.!
Bei Wärmetauscher ist p = konst.
Q!
Q!
"!
e!
k!
wL!
+++ © 2007 by René Sigrist +++ V1.0 +++ Fehler bitte melden an: [email protected] +++ Tabellenangaben beziehen sich auf: Taschenbuch der Physik, ISBN 3-446-22883-7 +++
Quergleichung
Quergleichung
Quergleichung
gerades Rohrstück
Bei Rohrkrümmungen entstehen
verschiedene Druckvektoren.
Grenzschicht
turbulent =
Re > 2320
siehe Bohl S.477
Als Grenzschicht wird eine dünne Schicht um einen umströmten Körper
bezeichnet. Durch die Zähigkeit des Fluids werden Schubkräfte übertragen.
Das Fluid hat an einer Wand die Wandgeschwindigkeit w = 0.
Reibungskräfte
%lam
Dicke turbulente Grenzschicht
Dicke laminare Grenzschicht
%turb
Werte aus VDI-Tabellen übernehmen. (Bohl S. 459)
Newton)sches Fluid: # = konst.
Ebene Platte
w*
x
la
y
Rekrit + 3.2 * 105 bis 3 * 106
Re-Werte: Bohl S. 475
Rekrit"
&"
l"
dh"
A"
U"
d"
k"
Thermo- / Fluiddynamik
Kräfte umströmter Körper
Grenzschicht und Ablösung
0° ist der vordere Staupunkt, 180° ist der hintere Staupunkt
F = m ! w
, (Bohl S. 472/473)
T in °K
2
! "1
1.6666
3
1.4
5
1.333
6
1-atomig 2-atomig - 3-atomig
f =
s= konst, ds = 0
Kapitel 3
Strömung, Quergleichung, Isentrope Zustandsänderungen
Isentrope Zustandsänderungen
thermische Zustandsgrössen (ideales Gas):
spezische Arbeit w!->" geschlossenes System (ideales Gas, # = konst.)
Wasserdampf
Freiheitsgrad f
[m/s2]
[-]
[-]
[-] (Bohl S. 472/473)
[N]
[W]
[m/s]
Isentropenexponent ,
Erdbeschleunigung (9.81)"
Renoldszahl"
Archimedeszahl"
Isentropenexponent"
Leistungskraft"
Leistung"
Leitungsgeschw."
Sinkgeschwindigkeit
g"
Re"
Ar"
,"
FL"
P"
wL"
Isentropenexponent #
spezische Arbeit w!->" offenes System (ideales Gas, # = konst.)
mittlere Geschwind."
[m/s]
turb. Druckdifferenz"
[Pa]
turb. Winderstandsbeiwert" [-] (Bohl S. 164/165)
Reibungskraft"
[N]
Widerstandsb. Oberäche" [-] (Bohl S. 272)
Widerstandsb. Form"
[-]
Widerstandsb. Gesamt"
[-] (Bohl S. 486/487)
Oberächenleistung"
[W]
Re
Widerstandskraft
Wenn bei ReBestimmung w
unbekannt ist,
w=2 m/s
annehmen und am
Ende überprüfen.
md = Festkörper
mk = Fluid
Bsp. Flügel
Reibungskräfte an Grenzschichten von umströmten Flächen
Widerstandskräfte an umströmten Körpern
p
!"
wm"
'pturb"
(turb"
FR"
cF"
cD"
cW"
PO"
Auftriebskraft
ASpant = Projektion des Körpers
quer zur Hauptrichtung.
FL =
Sinkgeschwindigkeit
[-]
[]
[m]
[m]
[m2]
[m]
[m]
[mm]
Gewichtskraft
cW
Reynoldszahl"
Scherung"
Rohrlänge"
hydr. Durchmesser"
Querschnittsäche"
Querschnittsumfang"
Durchmesser"
Rauigkeitswert"
+++ © 2007 by René Sigrist +++ V1.0 +++ Fehler bitte melden an: [email protected] +++ Tabellenangaben beziehen sich auf: Taschenbuch der Physik, ISBN 3-446-22883-7 +++
[kg/m3]
[m]
[m/s]
[Pa]
[m2/s] (Bohl S. 495ff)
[m]
[m]
[m]
hydr. Durchmesser verschiedener
Querschnitte: Bohl S. 174
Rohrströmung
Bei nicht runden Rohren bildet man ein Ersatzrohr-Modell mit kreisförmigen
Querschnitt, welches pro Kanallänge den selben Druckabfall aufweist wie
das originale Rohr.
ErsatzRohr
Dichte"
Rohrkrümmung"
Geschwindigkeit"
dyn. Viskosität"
kin. Viskosität"
Umschlagsstelle"
lam. Grenzschichtdicke"
turb. Grenzschichtdicke"
A (Querschnittsäche)
U (Querschnittsumfang)
unrundes
Rohr
!"
r"
w"
#"
$"
la"
%lam"
%turb"
Impulssatz
Reversible und irreversible Vorgänge (Zustandsgrösse Entropie)
Ein reversibler Vorgang ist ein Vorgang, der sich vollständig rückführen lässt,
ohne dass in der Umgebung eine Veränderung zurückbleibt.
Ein irreversibler Vorgang lässt sich nur rückführen, wenn in der Umgebung
bleibende Veränderungen gemacht werden.
Gibb!sche Hauptgleichung
Die Entropie S ist eine Zustandsgrösse, die Reversibilität bzw. Irreversibilität
anzeigen kann.
geschlossenes System
offenes System
nur für f = konst.
Für s = konst. wird mit der Isentropengleichung gerechnet
Für s " konst. wird mit der idealen Gasgleichung gerechnet
Kreisprozesse
Ein geeignetes Medium durchläuft eine Serie von Zustandsänderungen, so
dass schlussendlich wieder der gleiche Zustand erreicht wird wie am Anfang.
Wirkungsgrad <1"
Volumen"
innere Energie"
spez. Volumen"
Freiheitsgrade"
Volumen"
Druckverhältnis"
[-]
[m3]
[J]
[m3/kg]
[-]
[m3]
[-]
T"
s"
p"
R"
$"
h"
u"
Temperatur"
spez. Entropie"
Druck"
spez. Gaskonstante"
Isentropenexponent"
spez. Enthalpie"
spez. innere Energie"
• Wärmekraft-Maschinen produzieren als Nutzen Wellenenergie. Dazu
benötigt werden zwei Wärmereservoire.
• Kältemaschinen und Wärmepumpen produzieren ein Wärmeresevoir (bei
Wärmepumpe Nutzwärme, bei Kältemaschinen Nutzkälte). Sie benötigen
mechanische Antriebsenergie und ein zweites Wärmereservoir.
!"
V"
U"
v"
f"
V"
#"
Der 2. Hauptsatz
Thermo- / Fluiddynamik
d# ist die Wärme, die im Inneren des Systems durch Reibungseffekte
entstanden ist, also dem System zugeführt wurde. Sie wird auch als
Reibungswärme bezeichnet. Die Grösse d# hat also die gleiche
Wirkung im System wie eine Wärmemenge dq, die von aussen über die
Systemwand transportiert wird.
Das T-s-Diagramm
Der 3. Hauptsatz Nernst!sches Wärmetheorem
Im 2. Hauptsatz interessieren vor allem die Entropieunterschiede
zwischen 2 Zuständen interessieren und der absolute Wert der Entropie
eines Zustandes weniger interessiert. Erst wenn durch chemische
Reaktionen die Substanzen in einem System von einem
Anfangszustand % in einen Endzustand & ihre Zusammensetzung
ändern, muss man eine gemeinsame Entropieskala anwenden. Daraus
entstand der 3. Hauptsatz:
Die (absolute) Entropie eines homogenen festen
Körpers, der sich in ungehemmtem thermischen
Gleichgewicht bendet, nähert sich dem Wert
Null, wenn sich die Temperatur dem absoluten
Nullpunkt nähert.
Kreisprozesse
Prozessanalyse
Zustandsänderungen in geeigneten Diagrammen einzeichnen
Involvierte Energiemengen (Arbeit und Wärme) identizieren
Apparativer Aufbau studieren
Nutzen und Aufwand bestimmen
Wirkungsgrad berechnen
•
•
•
•
•
Wirkungsgrad
w"
Geschwindigkeit"
[m/s]
Wärmemengen können im T-s-Diagramm sichtbar gemacht werden
Arbeitsmengen können im p-v-Diagramm sichtbar gemacht werden
[°K]
[J/kg°K]
[Pa]
[J/kgK°]
[-] (Bohl S. 472/473)
[J/kg]
[J/kg]
Kreisprozesse
Kapitel 3
Reversible Vorgänge, 2./3. Hauptsatz, Kreisprozesse
Wirkungsgrad Joule-Prozess
• Je grösser der Druckunterschied, desto besser der Wirkungsgrad
• Der theoretische thermische Wirkungsgrad hängt nur von der 1. Kompression ab,
und nicht etwa von T3
Für gute Wirkungsgrade:
• 1-atomige Gase (jedoch in Praxis problematisch)
• grosse Druckverluste
+++ © 2007 by René Sigrist +++ V1.0 +++ Fehler bitte melden an: [email protected] +++ Tabellenangaben beziehen sich auf: Taschenbuch der Physik, ISBN 3-446-22883-7 +++
Realer Kreisprozess am Beispiel Gasturbine
Bei realem Verdichter und Turbine gilt: d! > 0 ⇒ ds > 0
Temperatur"
spez. Entropie"
Druck"
spez. Gaskonstante"
Isentropenexponent"
spez. Enthalpie"
spez. innere Energie"
⇒ Die Entropie nimmt immer zu, auch bei Entspannung!
[-]
[m3]
[J]
[m3/kg]
[-]
[m3]
[-]
T"
s"
p"
R"
$"
h"
u"
Totalenthalpie-Zustände im Gasturbinen-Prozess
Wirkungsgrad <1"
Volumen"
innere Energie"
spez. Volumen"
Freiheitsgrade"
Volumen"
Druckverhältnis"
Beim Begriff Totalenthalpie geht
man von der Modellvorstellung
aus, dass die in einem
Strömungszustand vorhandene
kinetische Energie isentrop in
thermische Energie umgewandelt
wird, indem die Strömungsgeschwindigkeit auf 0 reduziert
wird. Damit kann sie auch in den
relevanten Diagrammen
eingezeichnet werden.
!"
V"
U"
v"
f"
V"
#"
[°K]
[J/kg°K]
[Pa]
[J/kgK°]
[-] (Bohl S. 472/473)
[J/kg]
[J/kg]
[m/s]
Isotherm
spezische Wärme
Geschwindigkeit"
Isotherm
Isochor
geschlossenes System: siehe Kuchling S. 296
offenes System:
spezische Arbeit
Thermo- / Fluiddynamik
w"
Isotrop
Isobar
+++ © 2007 by René Sigrist +++ V1.0 +++ Fehler bitte melden an: [email protected] +++ Tabellenangaben beziehen sich auf: Taschenbuch der Physik, ISBN 3-446-22883-7 +++
Isobar
Kapitel 3
Kreisprozesse