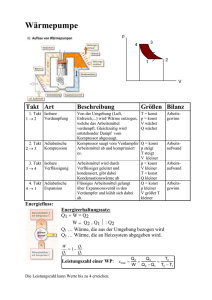
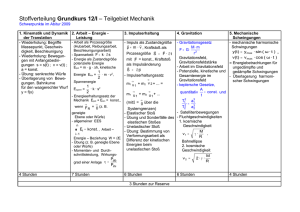
pV = konst.

Physik für Mediziner,
Zahnmediziner und
Pharmazeuten

SS2000
14.Vorlesung 26.5.2000
1
Prof. Dr. Alois Putzer
Zurück zur ersten Seite
Plan : Nächste Vorlesungen





Heute
Strömungen, Blutkreislauf
Anschließend : Wärme
Übungsblatt : (Lösungen werden in der
Vorlesung besprochen +Internet)
Folien ab jetzt auch als .pdf files
(6 Folien
/ Seite)
2
Zurück zur ersten Seite
Hagen-Poiseuille


Das Hagen-Poiseuille Gesetz beschreibt die Strömung einer Flüssigkeit durch ein Rohr mit Radius
R, Länge L und einer Druckdifferenz  p
Für den Volumenstrom (Volumen/Zeit) erhält man:
4
V  R p
IV 

t
8 L

Anwendungsbeispiel : Blutkreislauf
3
Zurück zur ersten Seite
Stokes

Das Gesetz von Stokes beschreibt die Bewegung
einer Kugel durch eine Flüssigkeit. Auf diese
Kugel wirken die Gewichtskraft G, die Auftriebskraft FA und die Reibungskraft FS.
  


F  ma  G  FS  FA
FS  6 RvS (Stokessch e Formel)


Wenn keine resultierende Kraft mehr auf die Kugel
wirkt, nimmt die Kugel eine konstante Geschwindigkeit vS ein (Sedimentationsgeschwindigkeit).
Aus der Sedimentationsgeschwindigkeit läßt sich
die Zähigkeit der Flüssigkeit berechnen.
4
Zurück zur ersten Seite
Anwendung: Blutsenkung
Laminare und turbulente Strömung

Reynoldsche-Zahl
Re 


2 R  v   Fl.

Kapillaren :
Re=0,01:lamina
r
Aorta:
Re=5000:turbulent
5
Zurück zur ersten Seite
Strömungsvorgänge


Strömung von Flüssigkeiten(später auch
von Wärme und Elektrizität)
Im menschlichen Körper spielen Ströme
eine wichtige Rolle
Transport energiereicher Moleküle zu
den Zellen
Sauerstofftransport im Blut
Transport von Medikamenten.
6
Zurück zur ersten Seite
Strömungswiderstand

Analog zum Ohmschen
Gesetz : U = R I
Δ p  R V IV
8 L
RV 
4
R
7
Zurück zur ersten Seite
Blutkreislauf
8
Zurück zur ersten Seite

Wärme
Temperatur,
Wärmemenge, -kapazität
Versuch: Wärmekapazität
Ausdehnung
Gasgesetze
Osmose, Diffusion (Stoffaustausch)
Tiefe Temperaturen
Lokalanästhesie,Kältetherapie
Wärmestrahlung, Wärmeleitung
Grundumsatz, Wärmehaushalt

9
Zurück zur ersten Seite
Temperaturabhängige Größen





Aggregatzustand
Länge (Volumen)
Elektrische Leitfähigkeit
Schallgeschwindigkeit
Reaktionsgeschwindigkeit
10
Zurück zur ersten Seite
Temperatur : Maß für die mittlere
Energie der Moleküle



Einheit der Temperatur T : [K] (Kelvin)
Für Wasser bei Athmosphärendruck:
Gefrierpunkt :
0 °C = 273,15 K
Siedepunkt : 100 °C = 373,15 K
Chemische Reaktionen im Körper sind
stark temperaturabhängig =>
Kerntemperatur muß annäher nd konstant
gehalten werden.
11
Zurück zur ersten Seite
Wärmemenge und Wärmekapazität




Wärmemenge (Wärmeenergie): Q [J]
1 J = 0,239 cal (Kalorie)
1 cal = 4,19 J
= Wärmemenge, um 1g Wasser
von
14,5 °C auf 15,5 °C zu
erwärmen
Zusammenhang zwischen Wärmemenge
Temperaturänderung:
ΔQ  C ΔT  c  m ΔT
C=Wärmekapazität des Körpers : [J/K]
c=spezifischeWärmekapazität : [J/gK]
12
Zurück zur ersten Seite
Längen- (Volumen-) Ausdehnung

Längenänderung
l(T)  l0 (1  αΔ T)
α  linearer Ausdehnung skoeffizie nt

Volumenänderung
V(T)  V0 (1  βΔ T)
β  3α (für α klein)


Bei thermischen Dehnungen treten sehr große
Kräfte auf.
Spannungen treten bei Temperaturänderung auf,
wenn man Materialien mit verschiedenen
Ausdehnungskoeffizienten fest miteinander
verbindet.
(Bi-Metall, Implantate)
13
Zurück zur ersten Seite
Ruhende Gase



3 Zustandsgrößen : Volumen V, Druck p
und Temperatur T
Gasmoleküle bewegen sich statistisch
(Brownsche Molekularbewegung)
Gesetz von Boyle-Mariotte:
p V = konst. (T = konst.)
14
Zurück zur ersten Seite
Isotherme (gleiche Temperatur)

pV = konst.
(T=konst.)
15
Zurück zur ersten Seite
Luftdruck


Am Erdboden:
Dichte : 1,2 kg/m³
Druck : 1013 hPa
Luftdruck und Dichte nehmen
exponentiell mit der Höhe ab.
16
Zurück zur ersten Seite
Geschwindigkeitsverteilung der
Gasmoleküle für verschiedene T.
17
Zurück zur ersten Seite
Wärme als thermische Energie





Ther mische Energie = kinetische und
potentielle Energie der Moleküle.
Bei Gasen tritt nur kinetische Energie auf. Die
Gesamtenergie(Wkin) ist die Summe der
kinetischen Energien aller Gasmoleküle.
Bei jedem Stoß der Gasmoleküle an die Gefäßwand wird der Impuls p=2mv übertragen.
pV = 2/3 Wkin
Bei steigender Temperatur steigt die
kinetische Energie der Gasmoleküle.
18
Zurück zur ersten Seite
Ausdehnung von Gasen(1)

Normzustand (V0) festgelegt bei:
T
= 273,15 K , p = 1013 hPa

Gase haben nur Volumenänderung:

Bei isobarer Erwärmung (p=konst.)

1
1

K
273,15
ΔT
V(T)  V0 (1 
)
273,15K
Bei 0K (absoluter Nullpunkt) ist für ideale
19
Gase V(T) = 0.
Zurück zur ersten Seite
Ausdehnung von Gasen(2)

Bei isochorer Erwärmung (V=konst.)

Isotherme (T=konst.)
ΔT
p(T)  p 0 (1 
)
273,15K
pV

Isochore (V=konst.)
p

proportional T
Isobare (p=konst.)
V

= konst
proportional T
Für ideale Gase:
.pV
20
= N k T = n R T (Erklärung später)
Zurück zur ersten Seite
Zustandsgleichung (Ideale Gase)


Unter Normalbedingungen nimmt 1 mol eines
idealen Gases das Molvolumen = 22,41 Liter
ein.
Zustandsgleichung für 1 mol
pV
= NA k T = R T
k = 1,38 10-23 J/K (Boltzmann-Konst.)
R = 8,31 J/(mol K)= molare Gaskonstante

Für beliebige Gasmengen:
p
V=nRT
n = Anzahl der Mole
21
Zurück zur ersten Seite