Zusammenfassung des ersten Semesters Welche
Werbung

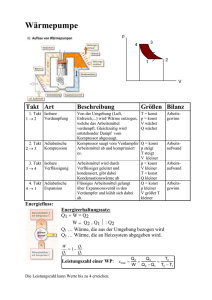
Zusammenfassung des ersten Semesters Welche Zusammenhänge sollten Sie wissen? (siehe Auflistung) • allgemeingültige „Drei-Buchstaben-Formeln“ • Grundlagen, insbesondere ⃗ und Drehmoment N ◦ die Newtonschen Axiome und die Bewegungsgesetze für Kraft F ◦ Zusammenhang zwischen Weg, Geschwindigkeit, Beschleunigung ◦ Zusammenhang zwischen Winkel, Winkelgeschwindigkeit, Winkelbeschleunigung ◦ Definition von Drehmoment, Drehimpuls, Trägheitsmoment ◦ Zusammenhang zwischen Kraft und potenzieller Energie ◦ Zusammenhang zwischen Kraft und Arbeit. ⃗ =0, F ⃗ =konst. , F =−k x (gleiches gilt für N ⃗ ) ◦ Lösung der Bewegungsgleichung für F ◦ Lösung der Bewegungsgleichung d. freien unged. Schwingung: nur harmonische Schwingung ◦ Ausdrücke für wichtige Energien (kinetische u. potenzielle Energie, Rotations -u. Spannenergie) ◦ Ersetzungsregeln Translation → Rotation ◦ Zusammenhang zwischen Kraft, Federkonstante, Masse und Kreisfrequenz einer Schwingung ◦ Zusammenhang zwischen Phasengeschwindigkeit, Kreisfrequenz und Wellenlänge einer Welle ◦ Zusammenhang zwischen dem Interferenzmuster an einzelnen oder mehreren Spalten und Breite und Abstand der Spalte ◦ Die Zusammenhänge für Drücke und Kräfte in ruhenden Fluiden ◦ Die Zusammenhänge für Drücke und Kräfte in strömenden Fluiden ◦ Den Zusammenhang zwischen Druck, Volumen und Temperatur eines idealen Gases. ◦ Den Zusammenhang zwishen Wärme, Masse und Temperaturänderung ◦ Die zwei Hauptsätze der Thermodynamik ◦ Den Zusammenhang zwischen Temperatur, Wärme und Entropieänderung Welche Methoden sollten Sie anwenden können: • Kräfte und Drehmomente erkennen können und zeichnerisch und mathematisch bestimmen und addieren können • Systemgrenzen ziehen können und innere und äußere Kräfte und Drehmomente unterscheiden können ⃗ und N • Aufstellen von Bewegungsgleichungen für F • Lösen eine Bewegungsgleichung durch Trennung der Variablen • Durch Einsetzen zeigen, dass eine Funktion eine Lösung einer Bewegungsgleichung ist. • Angeben einer konkreten Lösung einer Bewegungsgleichung aufgrund gegebener Anfangsbedingungen • Anwenden von Impuls- , Drehimpuls- und Energieerhaltung für isolierte und offene Systeme ◦ Dazu müssen Sie bei offenen Systemen die Arbeit berechnen können. und N ⃗ • Anwenden der Gleichgewichtsbedingung für F • Anwenden von Scheinkräften im beschleunigten Bezugessystem (Trägheits-, Zentrifugal,Crioliskraft) ◦ Dazu müssen Sie erkennen können, wann ein Inertial- und wann ein beschleunigtes Bezugssystem vorliegt. • Anwenden der reellen und komplexen Schreibweise für Schwingungen und Wellen ◦ Dazu müssen Sie die Bedeutung von Amplitude und Phase erkannt haben und die Eulersche Formelanwenden können. Welche mathematischen Methoden sollten Sie anwenden können? • Grundrechenarten, sicherer Umgang mit Brüchen, Potenzen und Winkelfunktionen • Umgang mit Vektoren, grafisch und mathematisch, insbesondere Zerlegung von Vektoren, Addition und Subtraktion, Skalarprodukt, Kreuzprodukt, Rechte-Hand-Regel, Daumenregel • Differenzieren und Integrieren einfacher Funktionen, grafisch und mathematisch, (f(x) = konst., f(x) = x; f(x) = x2, f(x) = xn, f(x) = sin(x) oder cos(x) sollten Sie rechnerisch und grafisch integrieren und differenzieren können! • alle Methoden der mathematischen Ergänzung Auflistung: Welche Zusammenhänge sollten Sie kennen und anwenden können? Einheiten und Einheitenvorsätze kg, m, s, J, N, W, K, rad; pico, nano, mikro, milli, Kilo, Mega, Giga ⃗ = ⃗p˙ Bewegungsgesetz und Größen der Translation F a =⃗v˙ =⃗x¨ ⃗v =⃗x˙ ⃗ ⃗p =m ⃗v ˙ ⃗ = ⃗L N ⃗ =⃗r × F ⃗ ⃗ Bewegungsgesetz und Größen der Rotation N L =⃗r × ⃗p ω= φ̇ α ⃗ =ω ⃗˙ α= φ̈ ⃗ L =I ω ⃗ 2 2 gleichförmige Kreisbewegung ⃗ v =⃗ ω ×⃗r ; v=ω r ⃗ F R=−m ω ⃗r ⃗ F ZF =mω ⃗r I =mr 2 Bewegungsgleichungen und ihre Lösungen gleichförmige Bewegung F =0=m ẍ ⇒ x (t )= x 0+v 0 t ; 1 2 2 Harmonische Schwingung F =−D⋅x ⇒ ẍ+ω2 x=0 ⇒ x( t)= Asin (ω t+φ) gleichförmig beschleunigte Bewegung F =konst.=m ẍ ⇒ x (t )= a t +v 0 t +x 0 Kräfte Gewichts-, Reibungs- und Gravitationskraft F g =−mg F R=µ F N Auftriebskraft, Druckkraft F A =ρ Fluid V g Gleichgewichtsbedingung ∑ F i=0 i dF p =−∇ p dV ∑ N i =0 ω= √ D /m=2 π /T mM F G=−G 2 r i Arbeit, potenzielle Energie, Leistung x2 V2 W =∫ F a ( x)d x x1 P= dW ⃗ = F⋅⃗v dt W =∫ p d V ⃗E ⃗ kons =−∇ F pot V1 i ⃗ ⋅⃗ P= N ω Energiebilanzen isoliertes System E ges (t 1 )=E ges (t 2)=konst. Formen der Energie E ges=E kin+ E rot +E pot , g +E spann +E pot ,G ... 1 1 E kin= mv 2 E rot = I ω 2 E pot , g =mgh 2 2 Impuls- und Drehimpulsbilanzen pi (t 1)=∑ ⃗ p i (t 1)=konst. isoliertes System ∑ ⃗ t2 offenes System f E pot ( f )− E pot (i)=−∫ F kons( x)d x ⃗ dt p i (t 2)− ⃗ p i (t 1 )=∫ F ⃗ t1 offenes System 1 E spann= D x 2 2 E ges (t 2)−E ges (t 1)=W E pot ,G =−G ∑ L⃗i (t1 )=∑ L⃗i (t 1)=konst. t2 ⃗ dt L⃗ i (t 2)− L⃗i (t 1)=∫ N t1 Stoß: unelastisch mM r v f =v s elastisch v f =2 v s−v i Schwerpunktgeschw. v S= 1 (m v +m v ) m1 +m 2 1 1 2 2 Transformationen Galilei-Transformation ⃗ v =⃗v ' +⃗u ⃗ v '=⃗v −⃗ u Schwingungen und Wellen Kreisfrequenz, Frequenz, Periodendauer ω=2 π f Welle u (⃗r , t)= A⋅cos( ⃗ k⋅⃗r ±ω t±φ)=RE( A⋅exp [i ( ⃗ k⋅⃗r ±ω t±φ)]) f =1/T ω k =2 π/ λ ω=2 π/T Phasengeschwindigkeit, Kreisfrequenz, Wellenzahl c= k Phasengeschwindigkeit, Wellenlänge, Periodendauer, Frequenz c=λ f =λ /T Fluide Druck p=F / A Schweredruck p (h)= p0+ρ g h 1 2 p+ ρ v +ρ g y=konst. 2 Thermodynamik Ideale Gasgleichung p V =N k B T =n RT Wärmekapazität Q=c mΔ T B 1 Erster Hauptsatz der TD: Δ U =Q+W Entropiedifferenz S B−S A=∫ dQ T A Kontinuitätsgleichung ρ Av =konst. Bernoulli-Gleichung wichtige Wege, Flächen u. Volumina Kreisbogen s=r φ Kreisumfang L=2 π r Kreisfläche 4 3 A=π r 2 Kugelvolumen V = π r 3 Bezeichnungen q ; q Vektor und Betrag des Vektors t Zeit Kraft F m Masse x ; r ; s Ort, Weg v Geschwindigkeit a Beschleunigung p Impuls p Impulsbetrag oder Druck ⃗ Drehmoment N L Drehimpuls I Trägheitsmoment ; Winkelgeschwindigkeit oder Kreisfrequenz ; Winkelbeschleunigung (Polar)Winkel oder Phasenverschiebung W Arbeit Eges, Ekin , Erot … div. Energien P Leistung p Druck T Periodendauer oder Temperatur A Amplitude oder Fläche c Phasengeschwindigkeit einer Welle λ Wellenlänge V Volumen ρ Dichte kB Boltzmann-Konstante n, N Anzahl von Teichen oder Zuständen u Elongation, Auslenkung U innere Energie Q Wärme S Entropie q̇ Zeitableitung, q ' Ortsableitung, <...> Mittelwert Wann haben Sie einen Zusammenhang gelernt? Können Sie ihn in eigenen Worten wiedergeben und ohne Formelzeichen formulieren? Können Sie ihn in seinen Kontext einordnen, also in der Welt der Physik am richtigen Ort platzieren? Können Sie Bedingungen formulieren, wann dieser Zusammenhang zutrifft? Können Sie Beispiele nennen, auf die dieser Zusammenhang zutrifft oder nicht zutrifft? Können Sie ihn an einem Beispiel anwenden?