PN2 Einführung in die Physik für Chemiker 2: Übungsblatt 2

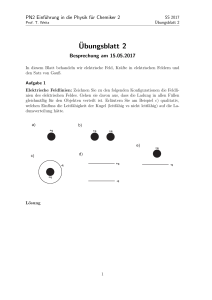
PN2 Einführung in die Physik für Chemiker 2
SS 2017
Übungsblatt 2
Prof. T. Weitz
Übungsblatt 2
Besprechung am 15.05.2017
In diesem Blatt behandeln wir elektrische Feld, Kräfte in elektrischen Feldern und
den Satz von Gauß.
Aufgabe 1
Elektrische Feldlinien: Zeichnen Sie zu den folgenden Konfigurationen die Feldlinien des elektrischen Feldes. Gehen sie davon aus, dass die Ladung in allen Fällen
gleichmäßig für den Objekten verteilt ist. Erläutern Sie am Beispiel c) qualitativ,
welchen Einfluss die Leitfähigkeit (leitfähig vs nicht leitfähig) der Kugel auf die Ladunsverteilung hätte.
a)
b)
+q
+q
+q
e)
+q
d)
c)
+q
-q
+q
-q
Lösung
1
-q
Aufgabe 2
Satz von Gauß: Berechnen Sie mit Hilfe des Gaußschen Satzes das elektrische Feld
~ innerhalb und außerhalb einer geladenen Hohlkugel und einer geladenen Vollkugel.
E
Nehmen Sie an, dass die Kugeln den Radius R und die Gesamtladung Q besitzen,
wobei die Ladung gleichmäßig auf der Kugelschale bzw. im Kugelvolumen verteilt ist.
Tipp: Unterscheiden Sie zwischen dem Feld E (r ) für r ≤ R und r > R.
Lösung: Für die Anwendung des Satzes von Gauß wählen wir eine Kugelschale mit
dem Radius r . Der Satz von Gauß hat dann folgende Form, die durch die Kugelsymmetrie weiter vereinfach werden kann.
I
I
Qinnen
Qinnen
~
~
⇒
E (r ) dA =
Φ=
E (r )d A =
0
0
A
A
Hier bezeichnet das Integral auf der linke Seite lediglich die Oberfläche 4πr 2 der Gaußschen Kugelschale. Betrachten wir zunächst den Fall r > R. Die eingeschlossenen Ladung ist sowohl für die Hohlkugel als auch für die Vollkugel gleich der Gesamtladung
Q, also Qinnen = Q.
I
Q
Q
E
dA =
⇒
E (r ) 4πr 2 =
0
0
A
Durch Umstellen ergibt sich:
E (r ) =
Q
40 πr 2
2
für r > R
Nun betrachten wir die Hohlkugel für r ≤ R. Da innerhalb einer Gaußfläche in der
Hohlkugel keine Ladungen sind, ist Qinnen = 0. Daraus ergibt sich sofort:
für r ≤ R
E (r ) = 0
Für die Vollkugel hängt die Ladung Qinnen , die innerhalb der Gaußfläche ist, vom
Radius r der Gaußfläche ab. Es gilt
Qinnen = Q
4
πr 3
3
4
πR 3
3
r3
=Q 3
R
Dann ergibt sich mit der Rechnung von oben
I
Qr 3
Qinnen
⇒
E (r ) 4πr 2 =
E
dA =
0
0 R 3
A
Und damit
E (r ) =
Qr
40 πR 3
für r ≤ R
Aufgabe 3
Millikan Versuch: Der Millikan-Versuch ermöglichte es bereits 1910, die Größe der
Elementarladung e relativ genau zu ermitteln. Dabei geht am wie folgt vor: Zunächst
wird Öl zu kleinen Öltröpfchen zerstäubt und in einen Plattenkondensator gebracht.
Durch Reibung z.B. beim Zerstäuben werden die Öltröpfchen zusätzlich aufgeladen.
Im feldfreien Fall erreichen die Öltröpfchen eine definierte Sinkgeschwindigkeit (durch
die Gravitation) die dazu benutzt werden kann, Tröpfengröße und Masse zu errechnen.
Daraufhin wird eine Spannung an den Plattenkondensator angelegt und so eingestellt,
dass das Öltröpfchen in Ruhe schwebt und somit die Gewichtskraft des Öltröpfchen
gerade durch die elektrische Kraft ausgeglichen wird. Aus dieser Spannung kann dann
die Ladung errechnet werden. Dies wollen wir im Folgenden nachvollziehen. Gehen
Sie davon aus, dass der Plattenkondensator einen Abstand von d = 1 cm hat. Das
Feld eines Plattenkondesators kann mit der angelegten Spannung U über die Formel
E = Ud in Zusammenhang gebracht werden.
a) Im feldfreien Zustand (U = 0V ) sinkt ein kugelförmiges Tröpfchen mit dem Radius
r mit konstanter Geschwindigkeit v nach unten, sobald nach einer vernachlässigbaren Beschleunigungsphase die Gewichtskraft durch die Auftriebskraft (aufgrund
der Verdrängung von Luft) und durch die Reibungskraft (Stokessches Gesetz)
kompensiert wird. Die Sinkgeschwindigkeit des Tröpfchens sei v = 5 · 10−5 m/s.
Berechnen Sie mithilfe der Viskosität der Luft η = 1,8 · 10−5 kg/(m s), der Dichte
der Luft ρLuft = 1, 2 kg/m3 , sowie der Dichte des Öls ρÖl = 0, 91 g/cm3 den Radius
r und die Masse m des Tröpfchens.
Lösung: Die Gewichtskraft FG , die Auftriebskraft FA und die Reibungskraft FR
sind durch folgende Gleichungen gegeben:
4
FG = mg = πr 3 ρÖl g
3
4
FA = πr 3 ρLuft g
3
3
FR = 6πηrv
Nach der Beschleunigungsphase ergibt sich eine konstante Geschwindigkeit, die
durch das Kräftegleichgewicht dieser Kräfte gegeben ist:
FR = FG − FA
=⇒
4
6πηrv = πr 3 (ρÖl − ρLuft )g
3
Einsetzen ergibt dann:
s
s
kg
9 · 5 · 10−4 ms · 1.8 · 10−5 m·s
9v η
r=
=
2(ρÖl − ρLuft )g
2(0.91 · 103 − 1.2) mkg3 · 9.81 sm2
4
m = πr 3 ρÖl
3
= 6.74 · 10−7 m
= 1.17 · 10−15 kg
b) Nun wird die Stärke des elektrischen Feldes über die Kondensatorspannung so
lange variiert, bis das Öltröpfchen regungslos schwebt. Dies stellt man bei einer
Spannung von U = 3.57 kV fest. Welche Ladung hat das Öltröpfchen? Im welchem
Zusammenhang steht diese Ladung zur Elementarladung e = 1.6 · 10−19 C?
Lösung: Zum Kräftgleichgewicht kommt nun auch noch die elektrische Kraft hinzu. Im Gleichgewichtsfall ist v = 0 und damit auch FR = 0:
⇒
FG = FA + FR + FE
FE = FG − FA
Die Kräfte lassen sich wie folgt darstellen:
4
FG − FA = πr 3 (ρÖl − ρLuft )g
3
FE = E · q =
U
q
d
Daraus ergibt sich für U = 3.57 kV:
q=
4
πr 3 (ρÖl
3
− ρLuft )g
d = 3.2 · 10−19 C
U
Das entspricht genau der doppelten Elementarladung
c) Erläutern Sie, wie man durch Wiederholung dieses Vorgehens die Elementarladung
bestimmen kann!
Lösung: Wenn dieses Vorgehen für weitere Tröpfchen durchgeführt wird, wird
man immer ein ganzzahliges Vielfaches der Elementarladung errechnen. Aus vielen
Messungen kann dann auf die Elementarladung rückgeschlossen werden
4