Streuung an Kristallen Die Struktur von kristallinen Festkörpern wird

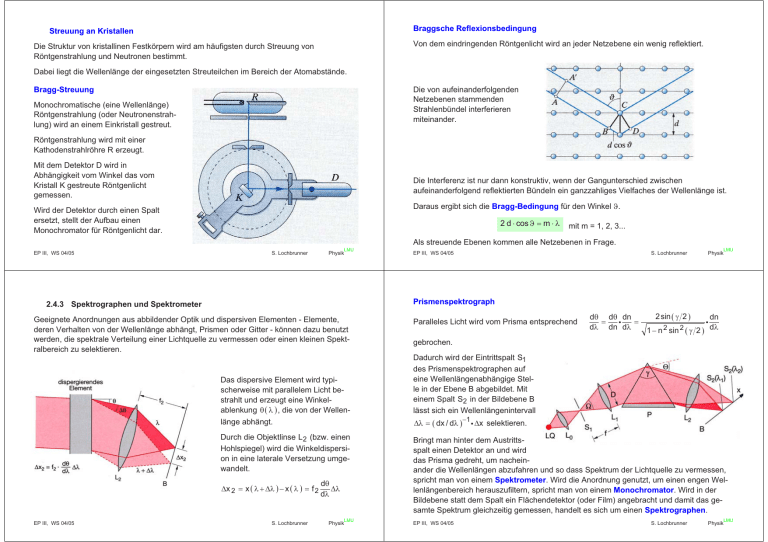
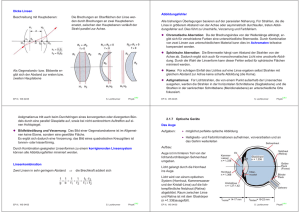
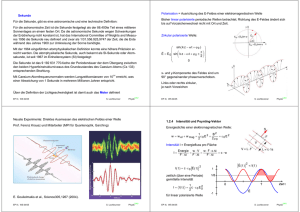
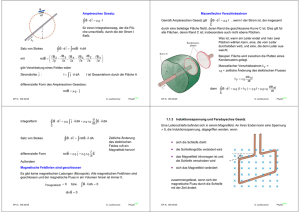
Braggsche Reflexionsbedingung
Streuung an Kristallen
Von dem eindringenden Röntgenlicht wird an jeder Netzebene ein wenig reflektiert.
Die Struktur von kristallinen Festkörpern wird am häufigsten durch Streuung von
Röntgenstrahlung und Neutronen bestimmt.
Dabei liegt die Wellenlänge der eingesetzten Streuteilchen im Bereich der Atomabstände.
Bragg-Streuung
Die von aufeinanderfolgenden
Netzebenen stammenden
Strahlenbündel interferieren
miteinander.
Monochromatische (eine Wellenlänge)
Röntgenstrahlung (oder Neutronenstrahlung) wird an einem Einkristall gestreut.
Röntgenstrahlung wird mit einer
Kathodenstrahlröhre R erzeugt.
Mit dem Detektor D wird in
Abhängigkeit vom Winkel das vom
Kristall K gestreute Röntgenlicht
gemessen.
Die Interferenz ist nur dann konstruktiv, wenn der Gangunterschied zwischen
aufeinanderfolgend reflektierten Bündeln ein ganzzahliges Vielfaches der Wellenlänge ist.
Daraus ergibt sich die Bragg-Bedingung für den Winkel-.
Wird der Detektor durch einen Spalt
ersetzt, stellt der Aufbau einen
Monochromator für Röntgenlicht dar.
2 d ˜ cos -
m˜O
mit m = 1, 2, 3...
Als streuende Ebenen kommen alle Netzebenen in Frage.
EP III, WS 04/05
LMU
S. Lochbrunner
Physik
S. Lochbrunner
LMU
Physik
Prismenspektrograph
2.4.3 Spektrographen und Spektrometer
Geeignete Anordnungen aus abbildender Optik und dispersiven Elementen - Elemente,
deren Verhalten von der Wellenlänge abhängt, Prismen oder Gitter - können dazu benutzt
werden, die spektrale Verteilung einer Lichtquelle zu vermessen oder einen kleinen Spektralbereich zu selektieren.
Das dispersive Element wird typischerweise mit parallelem Licht bestrahlt und erzeugt eine Winkelablenkung T O , die von der Wellenlänge abhängt.
Durch die Objektlinse L2 (bzw. einen
Hohlspiegel) wird die Winkeldispersion in eine laterale Versetzung umgewandelt.
'x 2
EP III, WS 04/05
EP III, WS 04/05
x O 'O x O S. Lochbrunner
f2
dT
'O
dO
LMU
Physik
Paralleles Licht wird vom Prisma entsprechend
dT
dO
dT dn
<
dn dO
2 sin J 2 <
dn
1 n 2 sin 2 J 2 dO
gebrochen.
Dadurch wird der Eintrittspalt S1
des Prismenspektrographen auf
eine Wellenlängenabhängige Stelle in der Ebene B abgebildet. Mit
einem Spalt S2 in der Bildebene B
lässt sich ein Wellenlängenintervall
'O
dx / dO 1 < 'x selektieren.
Bringt man hinter dem Austrittsspalt einen Detektor an und wird
das Prisma gedreht, um nacheinander die Wellenlängen abzufahren und so dass Spektrum der Lichtquelle zu vermessen,
spricht man von einem Spektrometer. Wird die Anordnung genutzt, um einen engen Wellenlängenbereich herauszufiltern, spricht man von einem Monochromator. Wird in der
Bildebene statt dem Spalt ein Flächendetektor (oder Film) angebracht und damit das gesamte Spektrum gleichzeitig gemessen, handelt es sich um einen Spektrographen.
EP III, WS 04/05
S. Lochbrunner
LMU
Physik
Um das einfallende parallele Bündel zu erzeugen, verwendet man einen Eintrittsspalt S 1,
der als Punkt- (Strich-) quelle dient und von dem austretendes Licht mit der Linse L 1 kollimiert wird.
Mit L 0 wird möglichst viel Licht der Lichtquelle LQ durch den Spalt gebracht.
Prismen haben eine hohe Transmission über einen sehr weiten Spektralbereich. Im UVBereich werden Prismen aus synthetischem Quarzglas oder CaF2 verwendet, im Sichtbaren Glasprismen (Schwerflintglas) und im IR Prismen aus Salzkristallen (z.B. NaCl).
Gitterspektrograph
Beim Gitterspektrometer und Gitterspektrograph erzeugt ein Gitter gemäß der Gittergleichung d ˜ sin D sin E m ˜ O eine wellenlängenabhängige Aufspaltung des Lichtbündels:
dE
dO
m
d < cos E
1
· 2
§ d 2 cos 2 D 2 d O
sin D O 2 ¸
¨¨
¸
m
m2
©
¹
Die Winkeldispersion hängt von der Gitterkonstante d, der Interferenzordnung m und der
Wellenlänge O ab.
Das einfallende Licht wird auf einen Eintrittsspalt fokussiert. In der Czerny-TurnerAnordnung wird das dann divergierende Lichtbündel mit einem "sphärischen" Spiegel
parallelisiert und auf das Gitter gelenkt. Das mit dem Gitter dispergierte Licht wird mit
LMU
einem
Hohlspiegel auf den Austrittsspalt fokussiert und dahinter
detektiert oder
auf
EP III, WSzweiten
04/05
S. Lochbrunner
Physik
zweiten Hohlspiegel auf den Austrittsspalt fokussiert und dahinter detektiert oder auf die
Bildebene abgebildet und mit einem Flächendetektor (z. B. CCD-Kamera) aufgenommen.
Beim Spektrometer wird durch Drehen des Gitters die vom Austrittsspalt transmittierte Wellenlänge verändert. Normalerweise wird dazu ein "Sinusantrieb" eingesetzt, um eine in guter Näherung lineare Wellenlängenskala zu bekommen.
Spektrales Auflösungsvermögen
Der Quotient O 'O wird als spektrales Auflösungsvermögen definiert. 'O ist der minimale
Wellenlängenabstand, für den noch getrennte Bilder des Eintrittsspaltes entstehen.
Ohne Beugung würde für monochromatisches Licht entsprechend der Brennweiten der
verwendeten Linsen / Spiegel ein Bild proportional zur Breite des Eintrittsspaltes beobachtet. Durch Verringerung der Spaltbreite könnte somit eine beliebig hohe Auflösung erreicht
werden.
Die Eintrittspupille - die Begrenzung des parallelen Strahlbündels - führt jedoch zu einem
Beugungsbild (Beugung am Einfachspalt), das bestenfalls invers-proportional zur Größe a
der Pupille ist. Es ergibt sich eine beugungsbedingte Divergenz 'T O a die Fußpunktsbreite 'xB 2 ˜ f2 ˜ O a.
EP III, WS 04/05
Für eng benachbarte Wellenlängen
ergeben sich leicht versetzte Beugungsstrukturen. Für gleiche Intensität
bei den beiden Wellenlängen können
diese genau dann noch unterschieden
werden, wenn das eine Beugungsmaximum mit dem ersten Minimum der
anderen Struktur übereinstimmt (Rayleigh-Kriterium).
Für das spektrale Auflösungsvermögen gilt dann
O
'O
a dT
<
2 dO
Eine hohe Auflösung lässt sich mit Gitterspektrographen erzielen. Die Breite des Pupille ist
a N < d < cos E und es folgt
O
d m ˜N
'O
Das Auflösungsvermögen ist also das Produkt aus der Anzahl N der beleuchteten Furchen
und der Interferenzordnung m. In der Praxis können für große Gitter mit hoher Strichzahl
Werte über 106 erreicht werden.
EP III, WS 04/05
S. Lochbrunner
LMU
Physik
PERKIN ELMER
Lambda 19
Spektralphotometer
S. Lochbrunner
LMU
Physik
= 2.4.4 Auflösung optischer Geräte
%
Fluoreszenz-Spektrometer
'
Messung der
spezifischen
Fluoreszenz, die eine
Probe nach selektiver
Anregung emittiert.
= ':
<
,% %
. %
%
Bei perfekter Abbildung hängt das Auflösungsvermögen von der Beugung des Lichtes an
den Begrenzungen (Pupillen) des optischen Systems ab. In der Regel sind die Begrenzungen rund und das Bild eines Punktes ein Airy-Scheibchen (Öffnungswinkel 'T O D ).
Fernrohr
;
,% >
%
* +
+
,%
+
'
+
%.
+
% -.
*
+
%
"
0
#/
#
$
0
0
- 12
- 12
Beugung an Objektivbegrenzung = Eintrittspupille mit Durchmesser D. Weit entfernte Objekte erscheinen unter Beobachtungswinkel H.
!
# /
/
!
!
"
5
% ,%
4
$
#
,
6 .
,%
+#
$"
-
"
0
#
&3
% %
78
#
;
%#
$
#
$9 &'(
%
#
!" )&'
$
Auflösung = minimales, beobachtbare H :
( )
% H minimal
,% . EP III, WS 04/05
S. Lochbrunner
Auflösung des Mikroskops
Fokussierung
Durch die Objektlinse L1 mit Durchmesser D entsteht ein
Zwischenbild, bei dem jedem Objektpunkt ein Beugungsscheibchen entspricht mit Fußpunktdurchmesser
d Beug 2,44 ˜ O ˜ b .
D
Wie groß ist der Brennfleck einer Sammellinse ?
Df
D
Der von L 1 erfasste maximale Öffnungswinkel ist
2 sin D D f
Fokussiert man ein Strahlenbündel mit Gauss-förmiger Intensitätsverteilung (typisch bei
Laserbündel) und einem Durchmesser D, so ergibt sich ein Fokusdurchmesser
Der Öffnungswinkel lässt sich durch Verwendung von Immersionsöl
mit n=1,5 verbessern.
EP III, WS 04/05
O
2n < sinD
0,61 <
O
NA
LMU
Physik
Wird die Linse mit Durchmesser D und Brennweite f homogen ausgeleuchtet (oder homogen ausgeleuchtete Kreisblende), gilt für den Durchmesser des Fokus' D f :
O˜f
D f 1,22 ˜
D
Nach dem Rayleigh-Kriterium muss der Abstand zweier
Punkte mindestens so groß sein, dass das erste Minimum der Beugung mit dem Maximum der anderen
Struktur zusammenfällt.
'x min 1 d Beug ˜ g
1,22 ˜ O ˜ g | 1,22 ˜ O ˜ f
2
b
D
D
1,22 <
1,22 ˜ O D
Teleskop:
große Öffnung Ÿ hohe Auflösung (geringe Beugung) und hohe Nachweisempfindlichkeit
'xmin
'T
Df
mit der numerischen Apertur
NA
S. Lochbrunner
n < sin D
LMU
Physik
4˜O˜f
S˜D
1,27 ˜
O˜f
D
Fokus ist schärfer bei größerem ursprünglichen Durchmesser, kürzerer Wellenlänge und
kürzerer Brennweite.
EP III, WS 04/05
S. Lochbrunner
LMU
Physik