29.5 Die Bindungsverhältnisse in Komplexen
Werbung
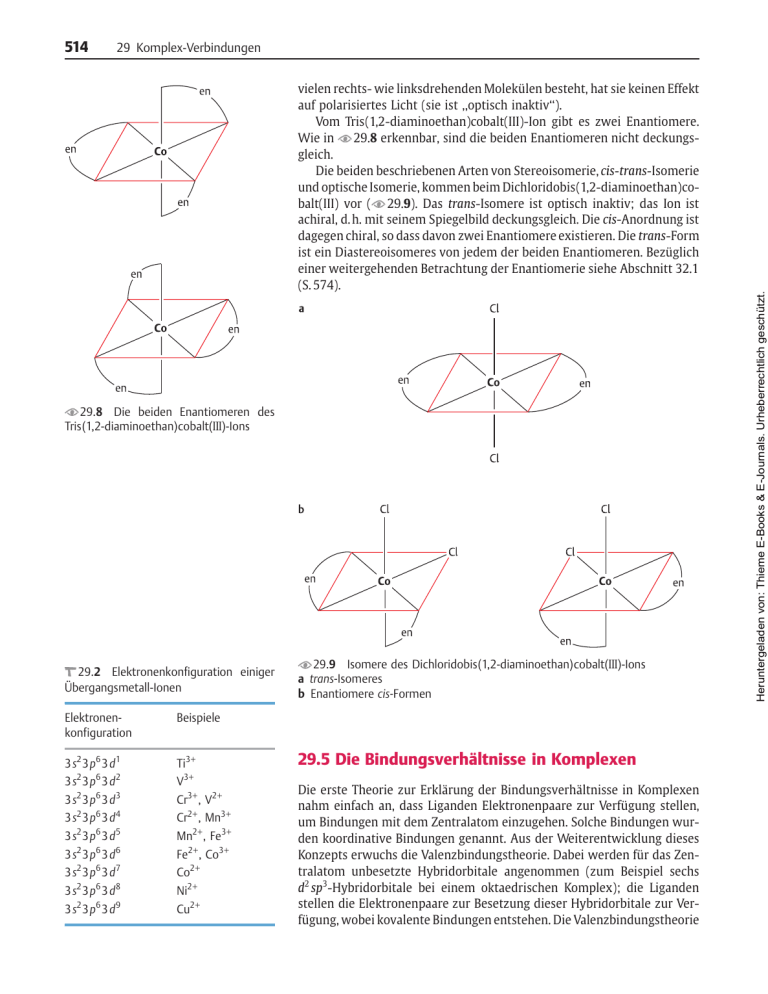
514 vielen rechts- wie linksdrehenden Molekülen besteht, hat sie keinen Effekt auf polarisiertes Licht (sie ist ,,optisch inaktiv‘‘). Vom Tris(1,2-diaminoethan)cobalt(III)-Ion gibt es zwei Enantiomere. Wie in 29.8 erkennbar, sind die beiden Enantiomeren nicht deckungsgleich. Die beiden beschriebenen Arten von Stereoisomerie, cis-trans-Isomerie und optische Isomerie, kommen beim Dichloridobis(1,2-diaminoethan)cobalt(III) vor ( 29.9). Das trans-Isomere ist optisch inaktiv; das Ion ist achiral, d. h. mit seinem Spiegelbild deckungsgleich. Die cis-Anordnung ist dagegen chiral, so dass davon zwei Enantiomere existieren. Die trans-Form ist ein Diastereoisomeres von jedem der beiden Enantiomeren. Bezüglich einer weitergehenden Betrachtung der Enantiomerie siehe Abschnitt 32.1 (S. 574). 29.8 Die beiden Enantiomeren des Tris(1,2-diaminoethan)cobalt(AAA)-Ions 29.2 Elektronenkonfiguration einiger Übergangsmetall-Ionen Elektronenkonfiguration Beispiele 3 s2 3 p6 3 d 1 3 s2 3 p6 3 d 2 Ti3 V3 3 s2 3 p6 3 d 3 3 s2 3 p6 3 d 4 Cr3, V2 Cr2, Mn3 3 s2 3 p6 3 d 5 Mn2, Fe3 2 6 6 3s 3p 3d 3 s2 3 p6 3 d 7 Fe2, Co3 Co2 3 s2 3 p6 3 d 8 3 s2 3 p6 3 d 9 Ni2 Cu2 29.9 Isomere des Dichloridobis(1,2-diaminoethan)cobalt(AAA)-Ions a trans-Isomeres b Enantiomere cis-Formen 29.5 Die Bindungsverhältnisse in Komplexen Die erste Theorie zur Erklärung der Bindungsverhältnisse in Komplexen nahm einfach an, dass Liganden Elektronenpaare zur Verfügung stellen, um Bindungen mit dem Zentralatom einzugehen. Solche Bindungen wurden koordinative Bindungen genannt. Aus der Weiterentwicklung dieses Konzepts erwuchs die Valenzbindungstheorie. Dabei werden für das Zentralatom unbesetzte Hybridorbitale angenommen (zum Beispiel sechs d2 sp3-Hybridorbitale bei einem oktaedrischen Komplex); die Liganden stellen die Elektronenpaare zur Besetzung dieser Hybridorbitale zur Verfügung, wobei kovalente Bindungen entstehen. Die Valenzbindungstheorie Heruntergeladen von: Thieme E-Books & E-Journals. Urheberrechtlich geschützt. 29 Komplex-Verbindungen 515 Heruntergeladen von: Thieme E-Books & E-Journals. Urheberrechtlich geschützt. 29.5 Die Bindungsverhältnisse in Komplexen 29.10 Grenzflächendarstellung für die d-Orbitale passt gut zu einer Reihe bestimmte andere nicht ungepaarten Elektronen dem macht sie keinerlei von experimentellen Beobachtungen, kann aber erklären. Insbesondere kann sie die Anzahl der bei manchen Komplexen nicht erklären, außerAussagen zu den Farben von Komplexen. Moderne Theorien zur Bindung in Komplexen wurden von der Kristallfeld-Theorie abgeleitet. In ihrer einfachsten Form nimmt sie elektrostatische Wechselwirkungen zwischen der positiven Ladung des zentralen Metall-Ions und den negativen Ladungen der Elektronenpaare der Liganden an. Ein wichtiger Aspekt ist dabei der Effekt, den das elektrische Feld der Liganden auf die d-Orbitale des zentralen Metall-Ions bewirkt. Die Außenelektronen von Übergangsmetall-Ionen sind d-Elektronen (vgl. 29.2). In einem isolierten Übergangsmetall-Ion sind alle fünf dOrbitale entartet, d. h. sie haben die gleiche Energie. Die Orbitale sind jedoch nicht mehr alle energetisch gleich, wenn sie unter dem Einfluss des elektrischen Felds von umgebenden Liganden stehen. Betrachten wir die Orientierung der d-Orbitale ( 29.10) relativ zur Anordnung der sechs Liganden in einem oktaedrischen Komplex ( 29.11 a). Die Orbitale dz 2 und dx 2 –y 2 weisen mit den Bereichen höchster Elektronendichte in Richtung auf die Liganden, während es bei den Orbitalen dxy, dxz und dyz die Richtung zwischen den Liganden ist. Es ergeben sich zwei Sätze von d-Orbitalen: 29.11 Anordnung der Liganden a in einem oktaedrischen b in einem quadratisch-planaren Komplex relativ zu einem Satz von kartesischen Koordinatenachsen 29 Komplex-Verbindungen 29.12 Diagramme, die veranschaulichen, dass die Linearkombination (Überlagerung) der Wellenfunktionen von einem dz2 – y2- und einem dz2 – x2-Orbital ein dz 2-Orbital ergibt. Die Vorzeichen bezeichnen das Vorzeichen der Wellenfunktion im jeweiligen Bereich. 1. die Orbitale dxy, dxz und dyz, im oktaedrischen Komplex als t2g-Orbitale bezeichnet, sind untereinander äquivalent, aber verschieden von 2. den Orbitalen dz 2 und dx 2 – y2, die ihrerseits untereinander äquivalent sind (eg-Orbitale) Die Symbole t2g und eg bringen zum Ausdruck, dass es sich um dreifach bzw. zweifach entartete Orbitale handelt (t = tripel-entartet, e = entartet). Es ist nicht sofort ersichtlich, dass ein dz2 -Orbital einem dx2 – y2-Orbital völlig gleichwertig ist. Ein dz2 -Orbital kann als Linearkombination von zwei Orbitalen dz2 – y2 und dz2 – x2 angesehen werden, welche die gleiche Gestalt wie das dx 2 – y 2-Orbital haben, aber anders orientiert sind ( 29.12). Da die Zahl der d-Orbitale auf fünf begrenzt ist, können die Orbitale dz2 – y 2 und dz2 – x 2 nicht unabhängig voneinander sein. In der Kristallfeld-Theorie wird ein elektrisches Feld angenommen, das von den negativen Enden der dipolaren Liganden-Moleküle oder von den als Liganden wirkenden Anionen um das zentrale Metall-Ion erzeugt wird. Ein Elektron in einem d-Orbital des Metall-Ions, das auf die Liganden ausgerichtet ist, hat wegen der elektrostatischen Abstoßung eine höhere Energie als ein Elektron in einem Orbital, das zwischen den Liganden ausgerichtet ist. Demnach haben in einem oktaedrischen Komplex die eg-Orbitale höhere Energien als die t2g-Orbitale. Die Differenz zwischen den Energien der eg- und der t2g-Orbitale in einem oktaedrischen Komplex wird mit o bezeichnet. In einem quadratisch-planaren Komplex ( 29.11b) sind viererlei Wechselwirkungen zwischen Liganden und d-Orbitalen zu berücksichtigen. Das dx 2 – y2-Orbital ist auf die Liganden ausgerichtet und hat die höchste Orbitalenergie. Das dxy-Orbital liegt in der Ebene der Liganden, ist aber zwischen diese ausgerichtet; seine Energie liegt unter der des dx 2 – y2-Orbitals. Die Elektronendichte des dz2-Orbitals ist hauptsächlich entlang der z-Achse konzentriert, aber der Ring in der xy-Ebene, auf den etwa ein Drittel der Elektronendichte kommt, steht in Wechselwirkung zu den Liganden. Das dz2-Orbital hat die nächst niedrigere Orbitalenergie. Die Or- Heruntergeladen von: Thieme E-Books & E-Journals. Urheberrechtlich geschützt. 516 29.5 Die Bindungsverhältnisse in Komplexen In einer erweiterten Fassung der Theorie, der Ligandenfeld-Theorie, werden kovalente Bindungsanteile berücksichtigt. Ähnlich wie bei der Elektronenpaar-Abstoßungs-Theorie (Abschn. 9.2, S. 122) wird die gegen- 29.14 Die energetische Aufspaltung von d-Orbitalen durch drei verschiedene Ligandenfelder 29.13 Die Verteilung von vier tetraedrisch angeordneten Liganden relativ zu einem kartesischen Koordinationssystem Heruntergeladen von: Thieme E-Books & E-Journals. Urheberrechtlich geschützt. bitale dxz und dyz sind entartet; sie werden vom elektrischen Feld der Liganden am wenigsten beeinflusst, da ihre Eleketronendichte aus der Ebene der Liganden hinausweist. Sie haben die niedrigste Energie. Die Aufspaltung der Orbitalenergien der d-Orbitale in einem tetraedrischen Komplex kann man sich durch Betrachtung von 29.13 überlegen. Die tetraedrisch angeordneten Liganden kann man sich in vier der acht Ecken eines Würfels denken; die Würfelflächen stehen senkrecht zu den Koordinatenachsen. Die Orbitale dxy, dxz und dyz sind auf die Kantenmitten des Würfels ausgerichtet, während die Orbitale dz2 und dx2 – y2 auf die Flächenmitten ausgerichtet sind. Der Abstand von einer Würfelecke zu einer Flächenmitte ist größer als der zu einer Kantenmitte. Infolgedessen werden Elektronen in den drei Orbitalen dxy, dxz und dyz stärker von den Liganden abgestoßen. Diese drei Orbitale werden im tetraedrischen Komplex mit t2 bezeichnet (ohne Index g für gerade, der nur bei zentrosymmetrischen Komplexen geschrieben wird). Die Energien der t2-Orbitale liegen höher als die der anderen beiden Orbitale, die mit e bezeichnet werden. Die energetische Abfolge von e- und t-Orbitalen ist im tetraedrischen Komplex somit umgekehrt wie im oktaedrischen Komplex. Die Differenz der Orbitalenergien im tetraedrischen Komplex wird mit t bezeichnet; sie ist etwa halb so groß wie o bei gleichem Zentral-Ion und gleichen Liganden. Die Aufspaltung der Energieniveaus der d-Orbitale in tetraedrischen, oktaedrischen und quadratisch-planaren Komplexen ist in 29.14 wiedergegeben. Ein Nachteil der Kristallfeld-Theorie ist ihre einseitige Betrachtung von elektrostatischen Wechselwirkungen, ohne Berücksichtigung des kovalenten Charakters der Bindungen. 517 518 29 Komplex-Verbindungen d s 29.15 Nichtbindende Überlappung eines s-Orbitals mit einem d-Orbital Noch umfassender ist die Molekülorbital-Theorie. Sie beschreibt die Bindungen durch das Auftreten von bindenden, nichtbindenden und antibindenden Molekülorbitalen. Alle Theorien kommen jedoch zum gleichen Schluss bezüglich der Aufspaltung der Energieniveaus und der Verteilung der d-Elektronen im zentralen Metall-Ion. Auf die Bedeutung der Aufspaltungen gehen wir weiter unten ein. Nach der Molekülorbital-Theorie kommt es in einem oktaedrischen Komplex zur Überlappung von je einem Orbital der sechs Liganden mit dem 4s-Orbital, den drei 4p-Orbitalen und dem 3dz2 und dem 3dx2 – y2Orbital des Zentralatoms, wobei sechs bindende und sechs antibindende Molekülorbitale entstehen. Die t2g-Orbitale dxy, dxz und dyz beteiligen sich an keinen -Orbitalen und verhalten sich nichtbindend (weder bindend noch antibindend, 29.15; die t2g-Orbitale können jedoch an -Bindungen mitwirken). Ein Molekülorbital-Diagramm für einen oktaedrischen Komplex ohne Berücksichtigung von -Bindungen ist in 29.16 gezeigt. Wenn zwei Atomorbitale unterschiedlicher Energie miteinander in Wechselwirkung treten, so entspricht der Charakter des entstehenden bindenden Molekülorbitals überwiegend demjenigen des Atomorbitals mit der niedrigeren Energie, und das antibindende Molekülorbital entspricht mehr dem Atomorbital mit der höheren Energie. In einem oktaedrischen Komplex entsprechen die bindenden Orbitale überwiegend den Orbitalen der Liganden. Die antibindenden Orbitale ähneln mehr den Orbitalen des Metall-Atoms. Die nichtbindenden t2g-Orbitale können als reine MetallAtomorbitale angesehen werden. 29.16 Molekülorbital-Diagramm für einen oktaedrischen Komplex ohne Bindungen Heruntergeladen von: Thieme E-Books & E-Journals. Urheberrechtlich geschützt. seitige Abstoßung zwischen bindenden Elektronenpaaren und den zusätzlich vorhandenen d-Elektronen betrachtet. 29.5 Die Bindungsverhältnisse in Komplexen Für oktaedrische Komplexe eines gegebenen Metall-Ions hängt der Betrag des Aufspaltungsparameters o von den Liganden ab. Für die Elektronenkonfiguration bestimmter Komplexe ist der Wert von o maßgeblich. Bei oktaedrischen Komplexen von Übergangsmetall-Ionen mit einem, zwei oder drei d-Elektronen (d1-, d2 oder d 3-Ionen) kommt je nur eine Elektronenkonfiguration in Betracht, unabhängig vom Betrag von o. Die d-Elektronen besetzen die t2g-Orbitale einzeln mit parallelem Spin. Dagegen haben Komplexe von Metall-Ionen mit vier, fünf, sechs oder sieben d-Elektronen jeweils zwei mögliche Elektronenkonfigurationen zur Auswahl ( 29.18). 29.17 Überlappung eines p-Orbitals mit einem d-Orbital zu einer p–dBindung Konfiguration des High-SpinZentralatoms Zustände Low-SpinZustände 29.18 Verteilung der Elektronen in oktaedrischen High-Spin- und Low-SpinKomplexen für d 4-, d 5-, d 6- und d 7-MetallIonen Heruntergeladen von: Thieme E-Books & E-Journals. Urheberrechtlich geschützt. In einem oktaedrischen Komplex werden die bindenden Molekülorbitale vollständig von den sechs Elektronenpaaren besetzt, welche die Liganden einbringen. Die Valenzelektronen des Zentralatoms besetzen die nichtbindenden t2g- und die antibindenden eg-Orbitale. Die Energiedifferenz zwischen diesen beiden Orbitalsätzen ist o. Die vier übrigen antibindenden Orbitale werden im Grundzustand bei keinem Komplex besetzt. Die Schlussfolgerung dieser Betrachtungsweise entspricht weitgehend den Aussagen der Kristallfeld-Theorie. In einem oktaedrischen Komplex kann man sich die fünffache Entartung der d-Orbitale des freien MetallAtoms aufgespalten denken, und zwar in einen dreifach entarteten Satz von Orbitalen, t 2g , und einen energetisch höherliegenden zweifach entarteten Satz von Orbitalen, eg. Der in 29.16 farbig hervorgehobene Teil mit den Molekülorbitalen, die von den d-Elektronen des Metall-Atoms besetzt werden, entspricht dem Diagramm gemäß der Kristallfeld-Theorie ( 29.14). Die 6 bindenden und 3 nichtbindenden Orbitale ergeben zusammen 9 Orbitale, die von 18 Elektronen besetzt werden können. Wenn dies der Fall ist, d. h. bei einem d 6-Ion (6 d-Elektronen), ist die 18-Elektronen-Regel erfüllt. Wir erkennen auch, warum die Regel oft nicht erfüllt wird: ob die nichtbindenden t2g-Orbitale besetzt sind oder nicht, macht kaum einen Unterschied aus. Die Besetzung der antibindenen eg-Orbitale führt zu einer Verminderung der Stabilität. Diese Stabilitätsverminderung ist oft gering genug, um toleriert zu werden; sie erklärt aber, warum zum Beispiel oktaedrische Cobalt(II)-Komplexe (d 7) weniger stabil sind als Cobalt(III)-Komplexe (d6) und warum oktaedrische Komplexe bei den Elementen am Ende des d-Blocks relativ selten sind. Eine zusätzliche Stabilisierung kann durch -Bindungen eintreten, die durch Wechselwirkung von p-Orbitalen der Liganden mit d-Orbitalen des Zentralatoms entstehen (p-d-Bindungen, 29.17). In einem oktaedrischen Komplex sind die t2g-Orbitale genau richtig orientiert, um solche Wechselwirkungen einzugehen. Wie bei einer -Bindung aus zwei p-Orbitalen ( 9.13b, S. 132) ergibt sich bei einer p-d-Bindung ein bindendes -Orbital, das energetisch unter dem Niveau des t2g-Orbitals liegt, und ein antibindendes *-Orbital, das darüber liegt. Die Besetzung des -Orbitals kann mit einem Elektronenpaar aus einem besetzten p-Orbital des Liganden erfolgen; das d-Orbital des Zentralatoms muss dann unbesetzt sein. Umgekehrt ist auch die Besetzung aus einem besetzten d-Orbital und einem unbesetzten p-Orbital möglich. Die Anwendung der Molekülorbital-Theorie auf tetraedrische oder quadratisch-planare Komplexe ist etwas komplizierter. Auch in diesen Fällen kommt man zu Energieterm-Aufspaltungen, die den Diagrammen von 29.14 entsprechen. 519 29 Komplex-Verbindungen High-Spin-Komplex: o < P Low-Spin-Komplex: o > P Spektrochemische Serie: A < Br < CB < F < OH < C2O 4 < H2O < NH3 < en < NO 2 < H < CN < CO Im Falle eines oktaedrischen Komplexes eines d 4-Ions kann das 4. Elektron eines der energetisch höher liegenden eg-Orbitale besetzen oder es kann sich mit einem der schon vorhandenen drei Elektronen in einem t2g-Orbital paaren. Im ersten Fall ergibt sich eine Konfiguration mit vier ungepaarten Elektronen; man spricht von einem High-Spin-Zustand. Im zweiten Fall sind nur zwei ungepaarte Elektronen vorhanden, man spricht von einem Low-Spin-Zustand. Welche der beiden Konfigurationen angenommen wird, hängt davon ab, welche energetisch günstiger ist. Um zwei Elektronen mit entgegengesetztem Spin auf das gleiche Orbital zu bringen, muss deren gegenseitige Abstoßung überwunden werden: es muss ein gewisser Energiebetrag, die Spinpaarungsenergie P, aufgebracht werden (wegen der Spinpaarungsenergie werden entartete Orbitale immer zunächst einfach besetzt: Hund-Regel). Wenn o kleiner als P ist, ist es günstiger, wenn das 4. Elektron eines der eg-Orbitale besetzt und keine Spinpaarung auftritt. Umgekehrt ist es günstiger, Elektronen zu paaren und die eg-Orbitale unbesetzt zu lassen, wenn 0 größer als P ist. Ob ein High-Spin- oder ein Low-Spin-Komplex entsteht, hängt somit von der relativen Größe der Energiebeträge 0 und P ab. Der Wert für P liegt im Allgemeinen in der Größenordnung von 200 kJ/mol und hängt vom Metall-Ion ab. Der Wert o ist von Komplex zu Komplex verschieden und hängt wesentlich von der Natur der Liganden ab. Die Schlussfolgerung gilt auch für Komplexe von d 5-, d6- und d7-Ionen. Für Komplexe von d 8-Ionen gibt es keine Wahl zwischen High- und LowSpin-Zustand; die einzige in Betracht kommende Konfiguration hat sechs gepaarte Elektronen in den t2g-Orbitalen und zwei ungepaarte Elektronen in den eg-Orbitalen. Entsprechend gibt es auch für Komplexe von d9- und d10-Ionen je nur eine mögliche Konfiguration. Werte für o können durch Messung der Absorptionsspektren der Komplexe erhalten werden. Im Falle des Komplexes [Ti(OH2)6]3 ist im Grundzustand nur ein Elektron in einem der t2g-Orbitale vorhanden. Durch Zufuhr von Energie, die dem Betrag von o entspricht, kann das Elektron angeregt werden und in ein eg-Orbital überwechseln. Anregungen dieser Art können durch Absorption von Licht zustande kommen. Das [Ti(OH2)6]3 zeigt ein Maximum der Lichtabsorption bei einer Wellenlänge von 490 nm; das entspricht einem Wert o = 243 kJ/mol. Das absorbierte Licht ist blau, es wird aber auch noch grünes Licht absorbiert. Rotes und violettes Licht werden nicht absorbiert, was dem Komplex seine rot-violette Farbe verleiht. Allgemein ergibt der Austausch von Liganden an einem gegebenen Metall-Ion eine Änderung der Energiedifferenz o und damit veränderte Bedingungen für die Lichtabsorption. In vielen Fällen beobachtet man auffällige Farbänderungen, wenn Liganden eines Komplexes durch andere ersetzt werden. In der spektrochemischen Serie werden die Liganden nach der Größe des von ihnen verursachten o-Wertes eingereiht. Bei der experimentellen Untersuchung der Spektren vieler Komplexe hat sich herausgestellt, dass die gleiche Reihenfolge bei Komplexen aller Übergangsmetalle überwiegend eingehalten wird; nur zwischen Liganden, die in der Serie nahe beieinanderstehen, gibt es gelegentlich Umkehrungen in der Reihenfolge. Die Spektrochemische Serie für häufig verwendete Liganden ist nebenstehend aufgeführt. Heruntergeladen von: Thieme E-Books & E-Journals. Urheberrechtlich geschützt. 520 Halogenid-Ionen verursachen in der Regel nur geringe Aufspaltungen der d-Orbitalterme, und Halogenido-Komplexe haben meist High-SpinKonfiguration. Das Cyanid-Ion, das am anderen Ende der Serie steht, induziert große o-Werte. Cyanido-Komplexe haben meist Low-Spin-Konfiguration. Ein gegebener Ligand bringt aber nicht immer Komplexe der gleichen Spin-Art mit sich. Zum Beispiel hat das Hexammineisen(II)-Ion eine HighSpin-Konfiguration, aber das isoelektronische Hexammincobalt(III)-Ion eine Low-Spin-Konfiguration. Für jedes Metall-Ion gibt es einen Punkt in der Serie, bei dem der Wechsel von high-Spin-erzeugenden zu low-Spin-erzeugenden Liganden eintritt. Zum Beispiel sind Cobalt(II)-Komplexe mit Ammoniak oder 1,2Diaminoethan High-Spin-Komplexe und solche mit Nitrit- oder CyanidIonen Low-Spin-Komplexe. Die Stelle, an der in der Serie der Wechsel von high-Spin- nach low-Spin-erzeugenden Komplexen erfolgt, hängt von der Spinpaarungsenergie P des Metall-Ions und vom Wert o des betreffenden Komplexes ab. Bei tetraedrischen Komplexen haben die zwei e-Orbitale niedrigere Orbitalenergien als die drei t2-Orbitale ( 29.14, S. 517). Für Komplexe mit d 1- und d 2-Ionen kommt jeweils nur eine Elektronenkonfiguration mit einfach besetzten e-Orbitalen in Betracht. Für ein d 3-Ion ( 29.19a) ist ebenso wie für ein d 4-, d 5- oder d 6-Ion jeweils ein High-Spin- und ein Low-Spin-Zustand denkbar. Tatsächlich kennt man jedoch bei tetraedrischen Komplexen nur High-Spin-Komplexe. In einem tetraedrischen Komplex ist die Energiedifferenz t zwischen den t 2- und e-Orbitalen relativ gering, nämlich etwa halb so groß wie o. Deshalb gilt für alle tetraedrischen Komplexe t < P. Wenn eine Alternative besteht, ist der Komplex mit ungepaarten Elektronen deshalb immer günstiger. Quadratisch-planare Komplexe treten bei d8-Ionen auf. Für diese ist ein High-Spin- und ein Low-Spin-Zustand denkbar ( 29.19b). Tatsächlich kennt man nur quadratische Komplexe mit Low-Spin-Konfiguration; da alle Elektronen gepaart sind, sind diese Komplexe diamagnetisch. Der Energieunterschied zwischen dem energetisch höchsten Orbital und dem energetisch darunter liegenden Orbital ist zu groß um eine High-Spin-Konfiguration zu ermöglichen. Für quadratische Komplexe von d 7-Ionen gilt das Gleiche; sie unterscheiden sich nur darin, dass im höchsten besetzten Orbital nur ein Elektron vorhanden ist. -Komplexe sind eine besondere Art von Komplex-Verbindungen, bei denen die Bindung über die Elektronen eines -Bindungssystems des Liganden vermittelt wird. Besonders zu nennen sind Verbindungen mit der Cyclopentadienid-Gruppe als Liganden. Im Cyclopentadienid-Anion, C5H 5, verfügen die fünf C-Atome des planaren Ringmoleküls über ein delokalisiertes -Bindungssystem mit 6 Elektronen (vgl. Abschn. 9.6, S. 138, und S. 548). Diese -Elektronen treten in Wechselwirkung mit unbesetzten d-Orbitalen eines Metall-Atoms, wobei sich das Metall-Atom genau über der Ringmitte befindet. Eine besonders stabile Verbindung ist Ferrocen, Fe(C5H5)2; es ist diamagnetisch und kann bis über 500 °C erhitzt werden ohne sich zu zersetzen. Das Fe-Atom befindet sich genau zwischen den beiden parallelen C5H5-Ringen. Verbindungen mit dieser Art von Aufbau werden auch Sandwich-Komplexe genannt. Ein anderer stabiler -Sand- high Spin low Spin high Spin low Spin 521 29.19 Verteilung der d-Elektronen in High-Spin- und Low-Spin-Zuständen: a in einem tetraedrischen Komplex eines d 3-Ions b in einem quadratisch-planaren Komplex eines d 8-Ions Ferrocen (Dicyclopentadienido-eisen; die Fünfecke symbolisieren C5H 5 -Ionen, die Kreise stehen für die je 6 delokalisierten -Elektronen) Heruntergeladen von: Thieme E-Books & E-Journals. Urheberrechtlich geschützt. 29.5 Die Bindungsverhältnisse in Komplexen 29 Komplex-Verbindungen Dibenzolchrom Dichloridodicyclopentadienidotitan wich-Komplex ist das Dibenzol-Chrom, Cr(C6H6)2, in welchem zwei Benzol-Moleküle (S. 137, 534) mit ihren -Elektronen an das Chrom-Atom gebunden sind. Die Ringe müssen nicht parallel sein, wie das Beispiel (C5H5)2TiCl2 zeigt. Auch einfache Moleküle mit -Bindungen wie zum Beispiel Alkene (Kohlenwasserstoffe mit CğC-Doppelbindungen) können über ihre Elektronen an Übergangsmetall-Atome gebunden werden. Die älteste bekannte Verbindung dieser Art enthält das Ion [(C2H4)PtCl3], das beim Einleiten von Ethen (C2H4) in eine wässrige K2[PtCl4]-Lösung entsteht. Komplexe dieser Art spielen eine Rolle als Zwischenstufen bei Reaktionen, bei denen Alkene im Beisein von katalytisch wirkenden Übergangsmetallverbindungen umgesetzt werden (z. B. bei der Ziegler-Natta-Polymerisation, S. 581). Übungsaufgaben (Lösungen s. S. 701) 29.1 Welche Oxidationszahl hat das Zentralatom in folgenden Komplexen? a) [Co(NO2)6]3 d) [Co(NH3)4Br2] g) [Ni(CO)4] b) [Au(CN)4] e) [Co(en)CB4]2 h) [PdCB 6]2 c) [V(CO)6] f ) [Fe(H2O)2CB 4] 29.2 Welche Ionenladung hat ein Komplex aus: a) Ag und 2 NH3 d) Pt4, 3 H2O und 3 Br 2 2 b) Co und 3 C2O4 e) Hg2 und 4 CB c) Au und 2 CN f) Cr und 6 CO 29.3 Geben Sie die Formeln für folgende Verbindungen an: a) Zink-hexachloridoplatinat(IV) b) Kalium-tetracyanidoniccolat(0) c) Tetramminchloridonitrito-N-cobalt(III)-sulfat d) Kalium-tetrabromidoaurat(III) e) Natrium-tetracyanidodioxidorhenat(V) f ) Tetramminplatin(II)-ammintrichloridoplatinat(II) g) Tetrammindithiocyanato-S-chrom(III)-diammintetrathiocyanato-S-chromat(III) h) Natrium-dithiosulfatoargentat(3−) i ) Kalium-aquapentachloridorhodat(III) j ) Tetramminkupfer(2+)-hexachloridochromat(3−) 29.4 Geben Sie die Namen für folgende Komplexe an: a) K4[Ni(CN)4] f ) [Co(NO)(CO)3] g) [Co(en)2(SCN)CB]CB b) K2[Ni(CN)4] c) (NH4)2[Fe(H2O)CB5] h) [Co(NH3)6]4 [Co(NO2)6]3 d) [Cu(NH3)4][PtCB4] i ) Na[Au(CN)2] e) [Ar(NH3)5(ONO)]CB2 29.5 Berechnen Sie die Komplexzerfallskonstante für das [AB(OH)4] -Ion aus folgenden Daten: 3 e + [AB(OH)4] AB + 4 OH 3 e + AB 3 AB E o = − 2,330 V E o = − 1,662 V 29.6 Bei Zusatz einer Lösung von Kaliumhexacyanidoferrat(II) zu Fe3 (aq) fällt ein Niederschlag von Kalium-eisen(III)-hexacyanidoferrat(II) aus, genannt Berliner Blau. Der gleiche Niederschlag entsteht bei Zusatz einer Lösung von Kaliumhexacyanidoferrat(III) zu Fe2 (aq). Welche Formel hat Berliner Blau? 29.7 Zwei Verbindungen haben die gleiche empirische Formel Co(NH3)3(H2O)2CBBr2. In einem Exsikkator verliert ein Mol der Verbindung A leicht ein Mol Wasser, Verbindung B jedoch nicht. Die elektrische Heruntergeladen von: Thieme E-Books & E-Journals. Urheberrechtlich geschützt. 522











