doppelspalt
Werbung

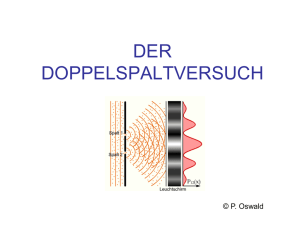
DER DOPPELSPALTVERSUCH © P. Oswald Experiment mit Kugeln Experiment mit Kugeln Experiment mit Kugeln Die Gesamtverteilung ist die Summe der Einzelverteilungen: P12(x) = P1(x) + P2(x) Experiment mit Wasserwellen Experiment mit Wasserwellen Experiment mit Wasserwellen Die Gesamtintensität ist nicht gleich der Einzelintensitäten I12(x) I1(x) + I2(x) Interferenz! Doppelspaltversuch mit Elektronen Doppelspaltversuch mit Elektronen Doppelspaltversuch mit Elektronen P12(x) P1(x) + P2(x) Zusammenfassung Klassische Teilchen Teilchen kommen stückweise an Gemessen wird die Wahrscheinlichkeit des Eintreffens Nres = N1 + N2 Es kommt zu keiner Interferenz! Klassische Wellen Wellen können jede Intensität besitzen Gemessen wird die Intensität der Wellen Ires ≠ I1 + I2 Es kommt zur Interferenz! Quantenobjekte Objekte kommen stückweise an Gemessen wird die Wahrscheinlichkeit des Eintreffens Nres ≠ N1 + N2 Es kommt zur Interferenz! Photonen - Doppelspalt Trotz gleichbleibender Bedingungen verhalten sich die Photonen unterschiedlich. Das Auftreffen ist zufällig! Alle Photonen landen zufällig auf dem Schirm. Die Gesamtheit der Photonen ergibt stets dasselbe Muster. Bei genügend hoher Anzahl von Photonen erinnert das Muster an eine Welle. -> Lichtausbreitung mit einer Welle erklären Welle steht für eine mathematische Beschreibung physikalischer Vorgänge. Photonen - Doppelspalt Die Welle gibt die Wahrscheinlichkeit an, mit welcher das Photon auf eine bestimmte Stelle treffen wird: helle Stellen: Auftreffwahrscheinlichkeit größer dunkle Stellen: Auftreffwahrscheinlichkeit geringer ! Es gibt keine Erklärung für die Zufälligkeit. D.h. es gibt keine Ursache, warum das Photon an einer bestimmten Stelle auftrifft. Zusammenhang: Welle - Wahrscheinlichkeit Der Zufall - die Wahrscheinlichkeit Im statistischen Mittel macht das Quantenteilchen (Elektron/Photon) das, was die Wahrscheinlichkeitswelle angibt. Max Born (Nobelpreis 1954): Die Wahrscheinlichkeit P, ein Teilchen an einem bestimmten Ort zu finden, ist Ψ 2 . Wobei Ψ die Amplitude der Wahrscheinlichkeitswelle ist. Es gilt p=| Ψ |2 p Wahrscheinlichkeit Ψ Amplitude der Wahrscheinlichkeitswelle Anmerkung: Ψ ist eine komplexe Funktion. Die Wahrscheinlichkeit ist stets >0. Ψ 2 könnte negativ sein. Welle - Teilchen Zusammenhang zwischen Teilchen und Wahrscheinlichkeitswelle: Louis de Broglie ordnete jedem Teilchen mit einem Impuls p die Wellenlänge λ=h/p zu. Für ein Photon gilt: p = h/λ Man spricht von Materiewellen. (Das sind Wahrscheinlichkeitswellen. Die Materie ist nicht wellenartig verteilt!) Materiewellen Louis de Broglie 1892 – 1987 Nobelpreis Louis de Broglie (1929 Nobelpreis) Beispiel: Die Wellenlänge eines Menschen mit m=80 kg und v=5 km/h ergibt sich zu λ=h/p=h/(mv)=6,6 *10-34 Js/(80*5000/3600) = 5,9*10-36m Für die Beugung solcher Wellen wären „Öffnungen“ dieser Größenordnung notwendig. Die mittlere Größe von Atomen liegt bei etwa 10-10m!!! Atomradien Wellenlänge eines Menschen mit m=80 kg und v=5 km/h: 5,9*10-36m Die Größe der Atomradien: Superposition • Superposition: Überlagerung verschiedener Möglichkeiten hier: die beiden Spaltdurchgänge • Der Aufenhaltsort ist unscharf • Bei Beobachtung (Messung)->Ort ist dann bestimmt – ansonsten bleibt er unbestimmt Photon am Doppelspalt • Photon trägt Information über Ort und Bewegung (Impuls) • Impuls eines Photons: p = h/λ Photon-> Welle zugeordnet • Verschiedene Impulse bedeuten Wellen mit verschiedenen Wellenlängen->Überlagerung: Wellenpaket Wellenpaket Animation mit Geogebra Sägezahn-/Rechteckskurve • Überlagerung von Funktionen können zu folgenden Ergebnissen führen: Sägezahnkurve Rechteckskurve Überlagerung: Sägezahn Sägezahn Sägezahn Sägezahn Sägezahn Sägezahn Rechteckskurve Rechteckskurve Rechteckskurve Schrödingergleichung • Mit dieser Welle wird die Wahrscheinlichkeit seines Aufenthaltsortes angegeben • Die Welle stellt eine Lösung der Schrödingergleichung dar: Ort und Impuls • Mit der Amplitude dieser Welle wird die Wahrscheinlichkeit seines Aufenthaltsortes angegeben • Zusammenhang: Ort - Impuls wenig Wellen-> langes Wellenpaket scharfer Impuls ungenauer Ort viele Wellen-> kurzes Wellenpaket unscharfer Impuls genauer Ort Heisenberg‘sche Unleichungen • Impuls und Ort: Δp* Δx>ħ/2 ħ=h/2π • Energie und Zeit: ΔE* Δt>ħ/2 Δp : Impulsunschärfe Δx : Ortsunschärfe ΔE : Energieunschärfe Δt : Zeitunschärfe h: Planck‘sches Wirkungsquantum • Erklärung des Tunneleffektes mit ΔE* Δt>ħ/2 Der Tunneleffekt Liefert eine Erklärung für: • Kernfusion in der Sonne • Alphazerfall • Tunneldiode • Rastertunnelelektronenmikroskop Quantisierung Stationäre Zustände • Nach der Schrödingergleichung gibt es verschiedene stationäre Zustände des Atoms -> Vergleich mit Saite • Sie lassen sich durch vier verschiedene Quantenzahlen ausdrücken: Hauptquantenzahl n Nebenquantenzahl l magnetische Quantenzahl –l ...+l Spinquantenzahl s Quantisierung von p und E Vergleich mit stehenden Wellen einer Saite: Teilchen ist nur dann stabil im Bereich l, wenn ihm eine “stehende” Materiewelle ψ(x) zugeordnet werden kann: z.B: I = 1*λ/2 =>λ=2l oder I = 2*λ/2 =>λ=l, … Für den Impuls p = h/λ heißt das, dass er quantisiert ist: Länge l n heißt Quantenzahl p proportional n E ist proportional n2 pn=n*h/2l, wobei n=1, 2, 3, … Ebenso gilt das für die Energie: E=p2/2m => En=n2*h2/(8l2m) Orbitale Aus ganz bestimmten Impuls- und Energiezuständen resultieren ganz bestimmte Aufenthaltswahrscheinlichkeiten, die mit | Ψ |2 beschrieben werden. Diese räumlichen Aufenthaltswahrscheinlichkeiten heißen Orbitale Das Pauliverbot Österreichischer Physiker 1945: Nobelpreis 1900 - 1958 Das Pauli-Verbot: in einem Atom gibt es keine Elektronen, die in all ihren Quantenzahlen übereinstimmen. Übersichtsfragen 1. 2. 3. 4. 5. 6. Was sind Quantenobjekte? Beschreibe das Doppelspaltexperiment Die Schrödingergleichung und Wellenfunktion Die Wahrscheinlichkeitswelle – was ist das? Die Bedeutung De Broglie‘s für die Quantenphysik Die Heisenberg‘sche Unschärferelation – Was sagt sie aus? 7. Der Tunneleffekt – Was versteht man darunter? 8. Die Quantenzahlen – Erläutere sie. 9. Das Pauliverbot – Was sagt es aus?