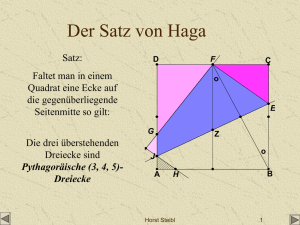
Geometrisches Denken

Mathematik Lerneinheit 2
Geometrisches
Denken
Arbeiten mit Unbekannten und
Parametern, Lösungsstrategien,
Kopfrechnen, Einsatz CASCAS-Rechner
Theorie, Übungen, Partnerinterviews,
dynamische Experimentiervorlagen,
Experimentiervorlagen,
Lernkontrollen
„Sag es mir, und ich vergesse es;
Zeige es mir, und ich werde mich erinnern;
Lass es mich tun, und ich behalte es.“
Konfuzius
Benno Frei ©2013/14
DialogMathe
Inhaltsverzeichnis
INHALTSVERZEICHNIS
1 Geometrische Grundbegriffe ......................................................................................................... 1
1.1
1.2
1.3
1.4
1.5
1.6
Gerade, Strahl und Strecke ....................................................................................................... 1
Winkel und Winkelarten .......................................................................................................... 2
Senkrecht und parallel .............................................................................................................. 3
Winkelpaare, Winkel an Parallelen......................................................................................... 4
Winkel im Dreieck ..................................................................................................................... 6
Winkel am Kreis ...................................................................................................................... 11
2 Winkelberechnungen .................................................................................................................... 13
2.1 Geometrische Denkaufgaben Winkel im Dreieck............................................................... 13
2.2 Geometrische Denkaufgaben Winkel am Kreis .................................................................. 26
3 Berechnungen von Dreieck und Viereck ................................................................................... 32
3.1
3.2
3.3
3.4
3.5
Symmetrien .............................................................................................................................. 32
Übersicht Vierecke................................................................................................................... 36
Strecken – und Flächenberechnungen .................................................................................. 41
CAS - Bausteine ....................................................................................................................... 43
Geometrische Denkaufgaben Dreieck und Viereck............................................................ 47
4 Berechnungen am rechtwinkligen Dreieck ............................................................................... 52
4.1
4.2
4.3
4.4
Sätze am rechtwinkligen Dreieck .......................................................................................... 52
Geometrische Denkaufgaben Pythagoras ............................................................................ 54
Spezielle rechtwinklige Dreiecke .......................................................................................... 60
Pythagoras und Kreisberührungen ...................................................................................... 64
5 Dreieckskonstruktionen................................................................................................................ 72
5.1 Geometrische Örter ................................................................................................................. 72
5.2 Dreiecksstücke ......................................................................................................................... 74
5.3 Konstruktionsbeschreibung ................................................................................................... 82
6 Streckenverhältnisse ...................................................................................................................... 88
6.1 Ähnliche Dreiecke ................................................................................................................... 89
6.2 Strahlensätze ............................................................................................................................ 94
6.3 Geometrische Denkaufgaben Strahlensätze und Ähnlichkeit .......................................... 98
7 Algebraische Behandlung von Geometrieaufgaben .............................................................. 102
7.1
7.2
7.3
7.4
7.5
Geometrische Denkaufgaben Lösungen mit dem CAS ................................................... 102
Geometrische Denkaufgaben Ansetzen einer Gleichung ................................................ 107
Trigonometrie am rechtwinkligen Dreieck........................................................................ 114
Flächeninhalt eines Dreiecks mit Trigo .............................................................................. 130
Pythagoras für beliebige Dreiecke ...................................................................................... 131
8 Kreisberechnungen ...................................................................................................................... 133
8.1 Kreisumfang ........................................................................................................................... 133
8.2 Kreisfläche .............................................................................................................................. 135
Lerneinheit 2 | Geometrisches Denken | 2013/14 |© BF
I
DialogMathe
9 Stereometrie ................................................................................................................................... 143
9.1
9.2
9.3
9.4
9.5
Oberflächen und Volumen einiger Körper ........................................................................ 143
Berechnungen mit Schnittebenen........................................................................................ 147
Ähnliche Körper .................................................................................................................... 148
Stereometrieaufgaben ........................................................................................................... 149
Rotationskörper, Guldinsche Regel .................................................................................... 151
„Sag es mir, und ich vergesse es;
Zeige es mir, und ich werde mich erinnern;
Lass es mich tun, und ich behalte es.“
Konfuzius
© DialogMathe
Mathematik Lerneinheit 2
Skript Geometrisches Denken 2013/14
Theorie, Übungen, Partnerinterviews, dynamische Experimentiervorlagen, Lernkontrollen
Von Benno Frei ©
II
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Vorwort
DialogMathe
Vorwort
Die Euklidische Geometrie ist die Geometrie der Ebene (Planimetrie) und des Raumes
(Stereometrie), die auf den von Euklid von Alexandria festgelegten Definitionen,
Postulaten und Axiomen beruht. Üblicherweise wird sie nur als Geometrie
bezeichnet. Es ist eine verbreitete Vorstellung, dass die euklidische Geometrie, wie
man sie in der Schule kennenlernt, „die“ (einzige) Geometrie sei. Das ist falsch:
Erstens wissen wir seit Einstein (Allgemeine Relativitätstheorie), dass unsere Welt
allenfalls lokal als euklidisch beschrieben werden kann. Andererseits wissen wir seit
Gauss, dass Geometrie mathematisch auch ganz anders gedacht werden kann.
Eine Theorie (z.B. die Geometrie) besteht aus Grundsätzen und Definitionen, aus
denen verschiedene Lehrsätze bewiesen werden. Die klassische Geometrie nach
Euklid unterscheidet sich von der nichteuklidischen Geometrie allein durch die
Gültigkeit des Parallelenaxioms. Dieses besagt, dass es zu jeder Geraden g und jedem
nicht auf dieser Geraden liegenden Punkt P genau eine zu g parallele Gerade h gibt,
die durch den Punkt P geht.
In der nichteuklidischen Geometrie, eine Geometrie, in der (fast) alle Axiome der
euklidischen Geometrie gelten mit Ausnahme des Parallelenaxioms, unterscheidet
man die hyperbolische und die elliptische nichteuklidische Geometrie: In der
hyperbolischen Geometrie gehen durch einen gegebenen Punkt mindestens zwei
Parallelen zu einer gegebenen Geraden. Die Winkelsumme im ebenen Dreieck ist
kleiner als 180°. In der elliptischen Geometrie, für die z. B. die Geometrie auf der
Oberfläche einer Kugel ein Modell ist, gibt es keine Parallelen, d.h. zwei Geraden
einer Ebene haben stets einen Punkt gemeinsam. Die Winkelsumme im ebenen
Dreieck ist grösser als 180°. Eine weitere Verallgemeinerung ist die riemannsche
Geometrie [nach G. F. B. Riemann]. Hier handelt es sich um ein System geometrischer
Sätze für n-dimensionale Räume, das die euklidische Geometrie und die
nichteuklidischen Geometrien als Spezialfälle enthält. Die riemannsche Geometrie
beantwortet die Frage nach möglichen Gestaltverhältnissen des Raumes. In ihr wird
der Begriff der Geraden, die zwei Punkte verbindet, ersetzt durch den Begriff der
kürzesten Linie (geodätische Linie) zwischen diesen Punkten, der Raum selbst kann
eine von Ort zu Ort veränderliche Krümmung haben. Die geometrischen
Eigenschaften dieses Raumes werden durch den Fundamentaltensor (metrischer
Tensor) beschrieben. Die riemannsche Geometrie ist das wichtigste mathematische
Hilfsmittel der allgemeinen Relativitätstheorie.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
III
Vorwort
DialogMathe
Die Grenze: Naturwissenschaft lässt sich mit Bildern popularisieren, aber nur mit
Mathematik verstehen (Auszug aus einem Artikel von Holm Tetens, Die Zeit 1999)
Wer würde nicht gern wissen, was die Welt im Innersten zusammenhält? Wann
immer die Wissenschaftler glauben, auf die letzten Bausteine der materiellen Welt
gestossen zu sein, melden sie uns Laien ihren Fund; unterstützt werden sie von einem
Heer von Wissenschaftsjournalisten. Es sind merkwürdige Meldungen.
Gegenwärtig werden wir überhäuft mit sensationell klingenden Berichten, wonach
Wissenschaftler mit dem Gedanken spielen, die Welt könne aus unvorstellbar kleinen
Fäden, "Superstrings" genannt, bestehen, die in einem elfdimensionalen "Raum"
schwingen. Von den elf Dimensionen liessen sich nur vier, die uns vertrauten drei
räumlichen Dimensionen und die Zeit als vierte Dimension, beobachten, die restlichen
sieben seien zu so unglaublich winziger Grösse "zusammengerollt", dass niemand sie
je beobachten wird. Nicht selten werden diese Schilderungen durch Bilder wild
ineinander verschlungener fadenartiger Gebilde illustriert. Haben wir uns die Bausteine der materiellen Welt also wie schwingende Fäden vorzustellen? Um Gottes
willen nein, eilig korrigieren sich die Wissenschaftler und Wissenschaftsjournalisten,
die Superstrings seien ganz und gar unanschaulich; die Rede und Bilder von Fäden
und die Metapher von zusammengerollten Dimensionen sollten wir nur ja nicht
missverstehen, es seien lediglich Krücken, damit wir Laien uns einem Verständnis der
unanschaulichen und eigentlich unvergleichlichen Superstrings wenigstens etwas
weiter annähern könnten. Genau beschreiben liessen sich die Superstrings nur in einer
unermesslich komplizierten Mathematik, so kompliziert, dass sie selbst die grössten
mathematischen Genies ins Schwitzen brächte. Es fragt sich, ob wir Laien nach
solchen und vielen anderen, aber ähnlichen Auskünften irgendetwas von dem
verstehen, was die Superstringtheorie über die Welt aussagt.
Und wer würde nicht gerne hinter das Geheimnis von Raum und Zeit kommen?
Die Wissenschaft, so erfahren wir Laien, habe sich in diesem Jahrhundert unter der
Federführung von Albert Einstein von den alltäglichen Vorstellungen von Raum und
Zeit für immer verabschiedet. Und wieder sind die uns Laien zugetanen Dolmetscher
aus Wissenschaft und Journalismus zur Stelle, diesmal um das ABC der Relativitätstheorie aufzusagen: Raum und Zeit seien untrennbar zu einem vierdimensionalen
Gebilde, "Raumzeit" genannt, "zusammengeschweisst", und diese Raumzeit werde
durch Materie "verbogen". Wieder sollen zweidimensionale Bilder raffiniert geformter
und verbogener dreidimensionaler Körper, Pferdesattel zum Beispiel, unserem Laienverstand auf die Sprünge helfen.
IV
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Vorwort
DialogMathe
Zurück zur Euklidischen Geometrie
In der euklidischen Geometrie spielen Dreiecke eine wichtige Rolle, da sich alle anderen Vielecke (Polygone) in Dreiecke zerlegen lassen. Wir werden uns also vorwiegend
mit Berechnungen von Dreiecken beschäftigen. Entscheidend ist aber das mathematische Denken, das wir entwickeln können, wenn wir uns mit der Geometrie auseinandersetzen. Definitionen sind die Grundbausteine, auf denen eine Theorie aufbaut.
Daraus lassen sich Aussagen (Sätze) als Folgerungen beweisen. Von Interesse sind
Strategien und Methoden für Problemlösungen.
Ziele der Lerneinheit geometrisches Denken
Inhaltsdimension
•
Winkelberechnungen, Dreieck, Kreis
•
Berechnung von Dreieck und Viereck
•
Pythagoras, Strahlensätze, Ähnlichkeit
•
Definition Sinus, Kosinus und Tangens am rechtwinkligen Dreieck
•
Trigonometrie: Berechnungen am rechtwinkligen Dreieck
•
Kreisberechnungen, Bogenmass
•
Stereometrie (räumliche Berechnungen)
Der Stoff, den wir in dieser Lerneinheit behandeln, hast du schon in der Sekundarschule kennengelernt. Es handelt sich daher vorwiegend um eine Repetition. Schau
dir die alten Hefte deiner früheren besuchten Schulen an!
Wir wollen jedoch nicht nur Kenntnisse auffrischen, sondern das wesentliche Ziel
wird sein, Zusammenhänge zu erkennen und die Mathematik zu verstehen. Zudem
können wir in der Geometrie algebraische Berechnungen durchführen. Daher wird
diese Lerneinheit auch eine Anwendung der Algebra sein.
Anwenden der Algebra
Erfassen von geometrischen Problemstellungen und Entwickeln von strukturierten
Lösungswegen mit Hilfe von Schaufiguren und mathematischen Sätzen. Algebraische
Behandlung, einführen von Unbekannten, ansetzen einer Gleichung (Lösungsprinzip:
für n Unbekannte brauchen wir n Gleichungen), Training im Kopfrechnen mit Hilfe
von geometrischen Denkaufgaben. Einsatz des CAS-Rechners für aufwendige Gleichungen oder Gleichungssysteme. Automatisieren von Berechnungen durch CASBausteine.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
V
Vorwort
DialogMathe
Handlungsdimmension
•
Modellieren und Transferieren
Modellieren erfordert, dass wir in einem gegebenen Sachverhalt die
relevanten mathematischen Beziehungen erkennen und diese dann in
mathematischer Form darstellen, allenfalls Annahmen treffen und
Vereinfachungen bzw. Idealisierungen vornehmen.
Transferieren erfordert ein adäquates Nutzen oder Übertragen fachlicher
Kompetenzen in den Alltag sowie in berufsfeldspezifische Bereiche.
•
Operieren und Technologieeinsatz
Operieren meint die Planung sowie die korrekte, sinnvolle und effiziente
Durchführung von Rechen- oder Konstruktionsabläufen oder das Arbeiten
mit Tabellen und Grafiken mit ein und beinhaltet immer auch die
zweckmässige Auslagerung operativer Tätigkeiten an die verfügbare
Technologie.
Technologieeinsatz: Mathematisches Tun wird heute in vielen Bereichen
durch die permanente Verfügbarkeit und Verwendung elektronischer
Werkzeuge unterstützt oder überhaupt erst ermöglicht. Dies gilt für nahezu
alle Ebenen mathematischen Arbeitens. Eine entsprechende
„Werkzeugkompetenz“ ist daher integraler Bestandteil mathematischer
Kompetenzen.
•
Interpretieren und Dokumentieren
Interpretieren erfordert, dass wir aus Informationen oder aus
mathematischen Darstellungen Fakten, Zusammenhänge oder Sachverhalte
erkennen und darlegen, sowie mathematische Sachverhalte und Beziehungen
im jeweiligen Kontext deuten.
Dokumentieren meint, Modelle, Lösungswege und Ergebnisse für sich und
andere brauchbar darzustellen und zu erläutern.
•
Argumentieren und Kommunizieren
Argumentieren begründet Entscheidungen oder erfordert die Angabe von
Aspekten, die für oder gegen eine bestimmte Sichtweise sprechen.
Argumentieren benötigt die korrekte und adäquate Verwendung
mathematischer Regeln sowie die Kenntnis der mathematischen Fachsprache.
Kommunizieren meint, kontextbezogene Informationen in
adressatengerechter Fachsprache auszutauschen
VI
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
DialogMathe
Vorwort
Notizen
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
VII
Vorwort
DialogMathe
Notizen
VIII
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Gerade, Strahl und Strecke
DialogMathe
1 Geometrische Grundbegriffe
1.1 Gerade, Strahl und Strecke
Punkte werden mit Grossbuchstaben benannt. Eine gerade Linie besteht aus
unendlich vielen Punkten.
Ist sie auf beide Seiten unbegrenzt, so nennen wir sie Gerade.
Ist sie in eine Richtung begrenzt und in die andere unbegrenzt, so heiss
sie Strahl.
Ist sie in beide Richtungen begrenzt, so nennen wir sie eine Strecke.
Strecken können wir messen (m, cm, usw.), z.B.: PQ ist die Länge der
Strecke PQ .
Geraden, Strahlen und Strecken werden mit kleinen Buchstaben oder mit
Hilfe der beiden Punkte benannt, die sie festlegen. Z.B.:
1.1.1 Gerade g durch die Punkte P und Q: PQ
1.1.2 Strahl s von P durch Q: PQ
1.1.3 Strecke a durch P und Q: PQ
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
1
Geometrische Grundbegriffe
DialogMathe
1.2 Winkel und Winkelarten
1.2.1 Bezeichnung von Winkel
Eine Figur aus zwei Strahlen mit gemeinsamem Anfangspunkt S heisst
Winkel. Die beiden Strahlen g und h sind die Schenkel des Winkels. Winkel
werden mit kleinen griechischen Buchstaben ( α : Alpha, β : Beta, γ : Gamma,
δ : Delta, usw.) benannt und in Grad gemessen.
Winkel α = 450
Der Winkel α kann durch die beiden Strahlen g und h oder durch die drei
Punkte P,S und Q festgelegt werden (S = Scheitel). α = ∢ ( g,h ) = ∢ PSQ
1.2.2 Winkelarten
2
Spitze Winkel
Rechter Winkel
Stumpfe Winkel
00 < α < 900
α = 90 0
900 < α < 1800
Gestreckter Winkel
Überstumpfe Winkel
Vollwinkel
α = 1800
1800 < α < 3600
α = 3600
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Senkrecht und parallel
DialogMathe
1.3 Senkrecht und parallel
1.3.1
Senkrechte Geraden
Zwei Geraden g und h heissen senkrecht
zueinander, wenn sie einen rechten
Winkel ( 900 ) einschliessen.
In Zeichen: g ⊥ h .
(Synonym für senkrecht: normal, orthogonal)
1.3.2 Parallele Geraden
Zwei Geraden g und h heissen parallel
zueinander, wenn sie eine gemeinsame
Senkrechte besitzen.
In Zeichen: g h .
g ⊥ s und h ⊥ s also g h
Zwei verschiedene parallele Geraden haben keinen Schnittpunkt.
1.3.3 Abstand
Der Abstand d bedeutet die kürzeste Entfernung.
Punkt – Punkt
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Punkt – Gerade
Gerade – Gerade
3
Geometrische Grundbegriffe
DialogMathe
1.3.4 Mittelsenkrechte
Die Mittelsenkrechte m AB zu einer Strecke AB
geht durch den Mittelpunkt von AB und ist
senkrecht zu AB .
Wenn ein Punkt P auf der Mittelsenkrechten von AB liegt, dann ist der Abstand von P zu A und von P zu B gleich.
Und Umgekehrt: Wenn der Abstand eines Punktes P zu A und zu B gleich ist,
dann liegt P auf der Mittelsenkrechten von AB .
1.3.5 Winkelhalbierende
Die Winkelhalbierende w α eines
Winkels α geht durch den Scheitel
S von α und halbiert α .
Wenn ein Punkt P auf der Winkelhalbierende w α eines Winkels α liegt, dann
ist der Abstand d von P zu beiden Schenkeln von α gleich.
Und Umgekehrt: Wenn der Abstand eines Punktes P zu beiden Schenkeln von
α gleich ist, dann liegt P auf der Winkelhalbierende w α .
1.4 Winkelpaare, Winkel an Parallelen
1.4.1 Nebenwinkel
α + β = 1800
→
4
β = 1800 − α
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Winkelpaare, Winkel an Parallelen
DialogMathe
1.4.2 Scheitelwinkel
Scheitelwinkel sind gleich gross.
α=β
1.4.3 Stufenwinkel an geschnittenen Parallelen
Die parallelen Geraden p und q werden von der Geraden g geschnitten.
Die Winkelpaare α und α '
heissen Stufenwinkel.
Stufenwinkel an Parallelen
sind gleich gross: α = α ' .
1.4.4 Wechselwinkel an geschnittenen Parallelen
Die parallelen Geraden p und q werden von der Geraden g geschnitten.
Die Winkelpaare β und β '
heissen Wechselwinkel.
Wechselwinkel an Parallelen
sind gleich gross: β = β ' .
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
5
Geometrische Grundbegriffe
DialogMathe
1.5 Winkel im Dreieck
1.5.1 Innenwinkel-Satz im Dreieck
Die Innenwinkelsumme im Dreieck beträgt
1800 .
α + β + γ = 1800
1.5.2 Aussenwinkel-Satz am Dreieck
Der Nebenwinkel α ' von α heisst
Aussenwinkel.
Es gilt: α '+ α = 1800
Und weiter
α' = β + γ
Der Aussenwinkel im Dreieck ist die Summe der beiden nicht anliegenden
Innenwinkel.
Aus α '+ α = 1800 (Nebenwinkel) und α + β + γ = 1800 (Innenwinkelsumme)
folgt: α '+ α = α + β + γ
/ −α
α' = β + γ
1.5.3 Gleichschenkliges Dreieck
c = AB heisst Basis, a, b Schenkel.
Da a = b liegen die Eckpunkte A und B auf
einem Kreisbogen mit Mittelpunkt C.
Die beiden Basiswinkel sind gleich: α = β .
Mit Hilfe der Innenwinkelsumme erhalten wir:
γ = 1800 − 2α
6
;
α=β=
1800 − γ
2
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Winkel im Dreieck
DialogMathe
1.5.4 Partnerinterview Innenwinkelsumme im n-Eck
Partnerinterview Innenwinkelsumme im n-Eck
Zeit: 15 Minuten
Problem 1
Zeige mit Hilfe der
nebenstehenden Figur dass die
Innenwinkelsumme im 3-Eck
1800 beträgt.
Problem 2
Berechne die Innenwinkelsumme eines 4-Ecks mit Hilfe der
Innenwinkelsumme des Dreiecks.
Analog die Innenwinkelsumme eines 5-Ecks, 6-Ecks, . . . . .
Verallgemeinere auf ein n-Eck (Gib eine Formel an!)
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
7
Geometrische Grundbegriffe
DialogMathe
1.5.5 Satz von Thales experimentell
Wir betrachten ein Dreieck, dessen
eine Seite AB der Durchmesser eines Kreises ist. Wählen wir die Ecke
C auf dem Kreis (Thaleskreis), so
ergibt sich immer ein rechtwinkliges Dreieck ( γ = 900 ).
Arbeiten mit dem dynamischen Geometrieprogramm von TI-Nspire
Wir können die Situation mit unserem Rechner aufzeichnen und den Winkel
γ messen, wobei wir die Ecke C dynamisch auf dem Kreis bewegen können.
Wir benutzen dafür Geometry.
Der TI-Nspire ist dokumentenbasiert.
Dokumente lassen sich in Ordnern
unter einem Namen abspeichern. Ein
Dokument kann maximale 30 Probleme
enthalten. Jedes Problem kann maximal
50 Seiten umfassen.
8
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Winkel im Dreieck
DialogMathe
1)
2)
3)
4)
5)
6)
7)
Strecke zeichnen
Mittelpunkt
Kreis
Punkt C auf Kreis
Winkel messen
Winkel Gradmass / Bogenmass
Ecke C auf Kreis verschieben
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
9
Geometrische Grundbegriffe
1.5.6
DialogMathe
Beweis Satz von Thales
Partnerinterview: Beweis Satz von Thales
Zeit: 10 Minuten
Versuche diesen Sachverhalt zu beweisen. Diskutiere mit deinem Lernpartner!
Benütze dazu die folgende Figur und die Eigenschaften von Dreieckswinkel.
10
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Winkel am Kreis
DialogMathe
1.6 Winkel am Kreis
α : Peripheriewinkel
β : Zentriwinkel
γ : Sehnen – Tangenten – Winkel
Für Peripheriewinkel und Zentriwinkel
über der gleichen Sehne AB gilt: β = 2α
Der Zentriwinkel ist doppelt so gross wie
der Peripheriewinkel.
Alle Peripheriewinkel über der gleichen Sehne AB sind gleich gross.
Für Peripheriewinkel und Sehnen – Tangenten – Winkel gilt: α = γ .
Peripheriewinkel und Sehnen – Tangenten – Winkel sind gleich gross.
Merke: Der Berührungsradius ZB steht rechtwinklig zur Tangente.
1.6.1 Dynamisches Arbeitsblatt Kreiswinkel
Dynamisches Arbeitsblatt
Peripheriewinkel
Zeit: 10 Minuten
Arbeitsaufträge
1) Bewege den Punkt Q auf der
Kreislinie. Was stellst du fest?
2) Wie ändert sich der Winkel, wenn
Q ausserhalb (innerhalb) des
Kreises liegt?
3) Verlängere die Sehne, indem du
einen Endpunkt auf dem Kreis
bewegst. Wie ändert
ä
sich der
Zentriwinkel und Peripheriewinkel.
4) Wähle den Durchmesser als Sehne. Wie gross wird dann der
Peripheriewinkel?
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
11
Geometrische Grundbegriffe
1.6.2
DialogMathe
Anwendung Kreiswinkel
Partnerinterview (Zeit: 15 Minuten)
1) Winkel im Sehnenviereck
2) Konstruktion eines Ortsbogen
1) Winkel im Sehnenviereck
Definition:
Ein Viereck, dessen vier Seiten Sehnen in einem
Kreis sind, nennen wir Sehnenviereck. Vierecke mit
einem Umkreis (alle Ecken liegen auf dem Kreis),
sind Sehnenvierecke.
Satz:
In einem Sehnenviereck ist die Summe von zwei
gegenüberliegenden Winkel 180o :
Beweis:
α + γ = 180o und β + δ = 180o
Zeige in untenstehender Figur, dass α + γ = 180o beträgt.
2) Konstruktion eines Ortsbogen
Bei geometrischen Konstruktionen (siehe Kap. 5 Dreieckskonstruktionen) muss häufig die folgende Problemstellung als
Grundaufgabe gelöst werden.
Wir suchen alle Punkte P, von denen die Endpunkte A und B
einer Strecke unter dem gleichen Winkel α gesehen werden.
Analysiere das Problem! Auf welcher Linie liegen alle
möglichen Punkte P? Betrachte den Spezialfall α = 90o .
Wie kann diese Linie konstruiert werden, wenn die Strecke
AB und der Winkel α gegeben sind?
12
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Winkel im Dreieck
DialogMathe
2 Winkelberechnungen
Mit den folgenden geometrischen Denkaufgaben kannst du deine
mathematischen Fähigkeiten anwenden und weiter entwickeln.
Lernziele
− Erfassen von geometrischen Problemstellungen und entwickeln von
strukturierten Lösungewegen mit Hilfe von Schaufiguren und
mathematischen Sätzen.
− Training im Kopfrechnen
− Algebraische Behandlung: Einführen von Unbekannten und aufstellen von
Gleichungen (Lösungsprinzip: Pro Unbekannte brauchen wir eine
Gleichung, d.h. für n Unbekannte brauchen wir n Gleichungen, so ergeben
sich Gleichungssysteme, die der Rechner lösen kann).
− Einsatz des Rechners: Erhalten wir bei der Lösung einer Aufgabe
Gleichungen, die wir noch nicht lösen können, so hilft uns der Rechner mit
dem solve – Befehl. Interpretiere jeweils die vom Rechner vorgeschlagenen
Lösungen.
2.1 Geometrische Denkaufgaben Winkel im Dreieck
− Beschreibe und begründe deine Lösungswege!
− Entwickle Strategien und wende diese auf neue Aufgaben an!
− Überprüfe die erhaltenen Ergebnisse auf Plausibilität!
− Diskutiere deine Lösungswege mit anderen. Kommuniziere mit Hilfe der
mathematischen Fachsprache.
2.1.1 Musterbeispiel
Berechne α .
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
13
Winkelberechnungen
DialogMathe
Lösungsvariante 1 (sequentielle Lösung, schrittweise Berechnung)
1) Hilfslinie AD
2) Winkel ∢ABD = 1800 − 1410 = 390 (Nebenwinkel)
3) Winkel ∢DAB = ∢ABD = 390 ( ∆ABD gleichschenklig)
4) Winkel ∢ADC = 2 ⋅ 390 = 780 (Aussenwinkel ∆ABD )
5) Winkel ∢DCA = ∢ADC = 780 ( ∆ADC gleichschenklig)
6) Winkel ∢CAD = 1800 − 2 ⋅ 780 = 240 (Innenwinkelsumme ∆ADC )
7) α = 390 + 240 = 630
oder Innenwinkelsumme ∆ABC : α = 1800 − 390 − 780 = 630
Lösungsvariante 2 (Einführen von Unbekannten, aufstellen von Gleichungen)
Unbekannte α, β, γ Innenwinkel des Dreiecks ∆ABC , Schaufigur entwickeln:
1) Hilfslinie AD
3) Winkel ∢DAB = β ( ∆ABD gleichschenklig)
4) Winkel ∢ADC = γ ( ∆ADC gleichschenklig)
5) Winkel ∢CAD = 1800 − 2γ (Innenwinkelsumme ∆ADC )
Gleichungen (3 Unbekannte / 3 Gleichungen)
14
Gleichung 1:
1410 + β = 1800 (Nebenwinkel)
Gleichung 2:
γ = 2β (Aussenwinkel ∆ABD )
Gleichung 3:
α + β + γ = 1800 (Innenwinkelsumme ∆ABC )
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Winkel im Dreieck
DialogMathe
Ersetzen wir Gleichung 1 durch α = β + 1800 − 2γ (Winkel bei A zweimal
ausdrücken α = ∢DAB + ∢CAD ), so ist das Problem unterbestimmt, d.h. es
gibt unendlich viele Lösungen.
Interpretation und Analyse der Rechnerlösung
Taschenrechnerlösung: α = 180 0 − 32 ⋅ c1 und β = 21 ⋅ c1 und γ = c1 , wobei die
Variable c1 eine beliebige Zahl sein kann (Einschränkungen durch die
Problemstellung: α, β, γ sind Dreieckswinkel).
Z.B. c1 = 400
→
α = 1200 , β = 200 , γ = 400 . Diese Lösung erfüllt die
Gleichung 1410 + β = 1800 , welche den Winkel β bestimmt, nicht. Warum
ergibt das zweite Gleichungssystem nicht die korrekte Lösung?
Gleichung 1:
α = β + 1800 − 2γ
Gleichung 2:
γ = 2β
Gleichung 3:
α + β + γ = 1800
→
→
→
α − β + 2 γ = 1800
−2β + γ = 00
α + β + γ = 1800
Die Informationen der Gleichung 1 sind schon in den Gleichungen 2 und 3
enthalten. Gleichung 1 bekommen wir, indem wir Gleichung 2 und 3
addieren, Gleichung 1 ist also abhängig von Gleichung 2 und 3. Unser
Problem hat 3 Unbekannte aber nur 2 Gleichungen (Bedingungen). Wir sagen
das Problem ist unterbestimmt (zu wenige Bedingungen).
MERKE:
Anzahl Unbekannte: So wenig wie möglich, so viel wie nötig !..
Wird beim Aufstellen von Gleichungen eine gegebene Information eines
Problems zweimal benutzt, dann erhalten wir unendlich viele Lösungen.
Je weniger Unbekannte ein Problem hat, desto besser ist die Überischt!
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
15
Winkelberechnungen
DialogMathe
2.1.2 Übungsbeispiele Winkel im Dreieck
Aufgabe 1
(w = AF = Winkelhalbierende)
Aufgabe 2
Aufgabe 3
Aufgabe 4
Lösungen A1: α = 120
16
A2: α = 600 / β = 750 / γ = 82,50
A3: α = 660
A4: α = 11,5 0
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
DialogMathe
Geometrische Denkaufgaben Winkel im Dreieck
Aufgabe 5
Aufgabe 6
Aufgabe 7
Aufgabe 8
Lösungen A5: α = 780 / β = 510 / γ = 270
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A6: α = 680
A7: α = 420
A8: α = 115, 5 0
17
Winkelberechnungen
DialogMathe
Aufgabe 9
Aufgabe 10
Aufgabe 11
Aufgabe 12
Lösungen
18
A9: α = 510
A10: α = 510
A11: α = 61, 5 0
A12: α = 75 0
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Winkel im Dreieck
DialogMathe
2.1.3 Repetitionstest Winkel im Dreieck
Repetitionstest : Winkel im Dreieck
Zeit: 45 Minuten
Löse die 5 Aufgaben ohne Hilfsmittel als Test.
Simuliere eine Prüfungssituation, arbeite mit einer Uhr. Zeit für eine Augabe
ca. 9 Minuten. Falls dir der Zugang zu einer Aufgabe innerhalb nützlicher
Frist nicht gelingt, überspringe sie. Ziel: In der vorgegebenen Zeit möglichst
viele gelöste Aufgaben!
Aufgabe 1
Aufgabe 2
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
19
Winkelberechnungen
DialogMathe
Aufgabe 3
Aufgabe 4
Aufgabe 5
Lösungen A1: α = 67, 5 0
A 2: α = 450 / β = 67,50 / γ = 78,750
A4: α = 250 / β = 750 / γ = 500
20
A3: α = 1000
A5: γ = 440
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Winkel im Dreieck
DialogMathe
2.1.4 Berechnungsaufgaben mit Parametern
In den folgenden Aufgaben sind keine konkreten Zahlen gegeben. Die Winkel
werden mit Hilfe von Platzhaltern sogenannten Parametern gegeben. Für diese können dann im Resultat verschiedene Zahlen eingesetzt werden. Dies
bringt den Vorteil, dass durch eine Rechnung mit den Parametern, unendlich
viele Zahlenbeispiele durchgerechnet werden können. Weiter können Bedingungen für die Parameter diskutiert werden (welche Zahlen sind möglich,
welche nicht?).
Aufgabe 1 Gegeben Winkel α ; Gesucht Winkel ϕ
Musterlösung
Lösungsidee: Winkel β = ∢ABC zweimal ausdrücken und gleichsetzen:
Innenwinkelsumme ∆FBC : 900 + ϕ + β = 1800
Gleichschenkliges Dreieck ∆ABC : β =
900 − ϕ =
1800 − α
2
→
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
ϕ=
→
β = 900 − ϕ
1800 − α
2
α
2
21
Winkelberechnungen
DialogMathe
Aufgabe 2 Gegeben Winkel α ; Gesucht Winkel ϕ
Aufgabe 3 Gegeben Winkel α , AD = AB = BC = s ; Gesucht Winkel ϕ
22
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
DialogMathe
Geometrische Denkaufgaben Winkel im Dreieck
Aufgabe 4 Gegeben Winkel α ; Gesucht Winkel ϕ
Aufgabe 5 Gegeben Winkel α , β ; Gesucht Winkel ϕ
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
23
Winkelberechnungen
DialogMathe
Aufgabe 6 Gegeben Winkel α ; Gesucht Winkel ϕ
Aufgabe 7 Gegeben Winkel α , DE = MB = r ; Gesucht Winkel ϕ
24
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Winkel am Kreis
DialogMathe
Aufgabe 8 Es ist AC = BC und AE = DE . Berechne den Winkel ϕ aus den
gegebenen Winkeln α und β .
2.1.5 Lösungen Berechnungsaufgaben mit Parametern
Aufgabe 1: ϕ =
α
2
Aufgabe 2: ϕ = 135 0 −
α
2
Aufgabe 3: ϕ = 3 α
Aufgabe 4: ϕ = 900 +
α
2
Aufgabe 5: ϕ = 1800 − 2α − 2β
Aufgabe 6: ϕ = 4α
Aufgabe 7: ϕ = 3 α
Aufgabe 8: ϕ = β − α
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
25
Winkelberechnungen
DialogMathe
2.2 Geometrische Denkaufgaben Winkel am Kreis
2.2.1 Übungsbeispiele Kreiswinkel
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Lösungen
26
A1: α = 360
A2: α = 660
A3: α = 440
A4: α = 790
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Winkel am Kreis
DialogMathe
Aufgabe 5
Aufgabe 6
Aufgabe 7
Aufgabe 8
Lösungen
A5: α = 240
A6: α = 1050
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A7: α = 100
A8: α = 67, 5 0
27
Winkelberechnungen
DialogMathe
2.2.2 Repetitionstest Kreiswinkel
Repetitionstest: Kreiswinkel
Zeit: 45 Minuten
Löse die 5 Aufgaben ohne Hilfsmittel als Test.
Simuliere eine Prüfungssituation, arbeite mit einer Uhr. Zeit für eine Augabe
ca. 9 Minuten. Falls dir der Zugang zu einer Aufgabe innerhalb nützlicher
Frist nicht gelingt, überspringe sie.
Ziel: In der vorgegebenen Zeit möglichst viele gelöste Aufgaben!
Aufgabe 1
Aufgabe 2
28
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Winkel am Kreis
DialogMathe
Aufgabe 3
Aufgabe 4
Aufgabe 5
Lösungen A1: α = 112, 5 0
A2: α = 1060
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A3: α = 1000
A4: α = 680
A5: α = 480
29
Winkelberechnungen
DialogMathe
2.2.3 Berechnungsaufgaben mit Parametern
Aufgabe 1 Berechne den Winkel α mit Hilfe einer Gleichung.
Aufgabe 2 Berechne den Winkel α aus β !
Aufgabe 3 Berechne ε aus α und β .
30
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
DialogMathe
Geometrische Denkaufgaben Winkel am Kreis
Aufgabe 4 Berechne die Winkel α und β .
Aufgabe 5 Berechne den Winkel α aus β !
Lösungen Kreiswinkel Berechnungsaufgaben mit Parametern
Aufgabe 1: α = 540
β
Aufgabe 2: α =
3
Aufgabe 3: ε = 900 + α − β
Aufgabe 4: α = 180 ; β = 330
Aufgabe 5: α = 2β − 1800
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
31
Berechnungen von Dreieck und Viereck
DialogMathe
3 Berechnungen von Dreieck und Viereck
3.1 Symmetrien
Symmetrie als Strukturprinzip in Natur und
Technik ist ein faszinierendes und in der
Mathematik ein überaus bedeutsames Thema.
Symmetrie leitet sich vom altgriechischen
symmetria her und bedeutet "Ebenmass". Ein
Objekt wird als symmetrisch bezeichnet, wenn
es gegenüber bestimmten Transformationen
unverändert (invariant) bleibt.
Transformationen dieser Art werden als Symmetrieoperationen bezeichnet.
Symmetrien führen vielfach zur Vereinfachung von Problemlösungen.
In der Physik spricht man u. a. von Symmetrie, wenn ein System im Verlauf
von Operationen, beispielsweise bei Umkehr der Zeitrichtung und einer
Raum-Zeit-Verschiebung, unverändert bleibt. Viele physikalische Systeme
gehorchen solchen Symmetrien, auf die sich auch die Erhaltungssätze der
Physik beziehen. Alle fundamentalen Wechselwirkungen, Gravitation, die
elektromagnetische, schwache und starke Wechselwirkung werden nach
heutigem Wissen durch Symmetrien (Eichtheorien) beschrieben. Das
Fundament der Naturgesetze ist vermutlich eine perfekte, grossartige
Symmetrie. Seit Albert Einstein ist die Physik auf der Suche nach einer
»Theorie für Alles«. Zwei Kandidaten gelten derzeit als vielversprechend: die
Stringtheorie und die Schleifen-Quantengravitation (»loop quantum gravity«).
Die Schleifen-Quantengravitation beschreibt den geometrischen Raum als
Verkettung winziger Quanten und Schleifen.
Stringtheorie [englisch string »Faden«]
Die Stringtheorie ist eine Klasse physikalischer Theorien, die als fundamentale
Gebilde submikroskopische, schwingende »Fäden« betrachten. Diese werden
als Urgebilde des Weltalls angesehen und sollen nach einer möglichen Stringtheorie als geschlossene Schleifen (Umfang 10−33 cm) einen zehndimensionalen
Raum bilden, in dem sie miteinander in Wechselwirkung stehen.
32
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Symmetrien
DialogMathe
Möglicherweise gestattet die Stringtheorie beziehungsweise die mit AnwenAnwe
dung der Supersymmetrie
Supers
entstandene Superstringtheorie eine einheitliche
Quantenfeldtheorie aller Wechselwirkungen der Elementarteilchen.
Symmetrieverletzungen
Die meisten Theorien
Theo
erfüllen jeweils die vorgegebenen Symmetrien,
allerdings nicht alle: Die Thermodynamik ist nicht T-invariant
invariant (Zeitumkehr),
da die Zunahme der Entropie eine Zeitrichtung auszeichnet - alltägliches Beispiel ist die zerbrochene Tasse, die sich nicht von selbst wieder zusammenzusam
fügt. Asymmetrien sind oft Hinweise auf tiefere Strukturen, so kann heute die
Supraleitung durch eine Symmetriebrechung erklärt werden.
Chiralität (Händigkeit)
Beim sp3-hybridisierten
hybridisierten Kohlenstoffatom weisen die vier Bindungen in die
Ecken eines Tetraeders. Sind vier verschiedene Atome bzw. Gruppen an ein
C-Atom
Atom gebunden, gibt es zwei Konfigurationen, d.h. zwei unterschiedliche
Möglichkeiten, diese
Gruppen anzu-ordnen. Man nennt
ein solches C-Atom
Atom
ein asymmetrisches
C-Atom
Atom (da sich
durch das Atom keine Spiegelebene legen lässt)
lässt) oder Chiralitäts-Zentrum.
Chiralitäts
Besitzt ein Molekül ein solches chirales C-Atom,
C Atom, existieren zwei KonfigurationsKonfigurations
Isomere, die sich wie Bild und Spiegelbild
Spi
bild verhalten: die zwei Enantiomere.
Enantiomere unterscheiden sich nicht in ihrem chemischen Verhalten und, mit
Ausnahme ihrer optischen Aktivität,, auch nicht in physikalischen EigenschafEigenscha
ten. Unterschiede gibt es jedoch
j doch in ihrem biochemischen Verhalten, denn im
Organismus kommt es zu Wechselwirkungen mit anderen chiralen MoleküMolek
len, bei denen die Konfiguration
Konfigur tion einen wesentlichen Einfluss hat.
Beispiel: Struktur der beiden
Enantiomere von Milchsäure.
Links (S)-Milchsäure,
Milchsäure, rechts
(R)-Milchsäure.
Milchsäure.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
33
Berechnungen von Dreieck und Viereck
DialogMathe
Biochemie
Viele biologisch wichtige Substanzen sind chiral, nicht nur die kleineren
Moleküle von Aminosäuren und Zuckern, sondern auch biologische
Makromoleküle wie Enzyme oder Rezeptoren. Bei einigen Substanzklassen
überwiegt oft ein Chiralitätssinn, so herrscht beispielsweise bei den
natürlichen Aminosäuren die L-Form vor. Chiralität als Folge des räumlichen
Baus von Molekülen hat entscheidende Bedeutung für das Funktionieren
biologischer Systeme, die alle selbst chiral sind. So sind viele Enzymreaktionen auf ein Enantiomer, entweder das linksdrehende oder das rechtsdrehende, spezialisiert, die Reaktionsgeschwindigkeit mit dem spiegelbildlichen
Enantiomer als Substrat ist dann deutlich geringer oder es wird gar nicht umgesetzt. Gar nicht so selten entfaltet das „falsche“ Enantiomer auch eine völlig
andere biologische Wirkung. Beispielsweise schmeckt bei einer bestimmten
Verbindung das eine Enantiomer süss, während sein Partner bitter ist. Bei
zahlreichen Geruchsstoffen unterscheidet sich der Geruchseindruck hinsichtlich Intensität und Ausprägung. Auch bei Pharmazeutika treten solche Effekte
fast regelmässig auf. Bei einigen Betablockern wirkt das eine Enantiomer
selektiv auf das Herz, das andere an den Zellmembranen des Auges.
Enzymreaktionen sind oft spezifisch für bestimmte Enantiomere, da das
aktive Zentrum eines Enzyms vielfach das eine Enantiomer leichter
aufnehmen kann als das andere. Das Enantiomere des Pharmawirkstoffes
D-Penicillamin, also das L-Penicillamin, ist toxisch. Deshalb ist eine hohe
Enantiomerenreinheit bei Arzneistoffen von überragender Bedeutung.
Geometrie
In der Geometrie ist die Symmetrie ein Merkmal bestimmter ebener und
räumlicher Formen. Unter Symmetrieoperationen versteht man Bewegungen,
die eine symmetrische Figur mit sich selbst zur Deckung bringen.
Die Symmetrieoperationen sind bezüglich eines gegebenen Punktes (Symmetriezentrum), einer Linie (Symmetrieachse) und einer Ebene (Symmetrieebene)
definiert.
34
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Symmetrien
DialogMathe
3.1.1 Achsensymmetrie
Eine geometrische Figur heisst achsensymmetrisch, wenn sie
durch Umklappen um eine Gerade a (die Symmetrieachse)
mit sich selbst zur Deckung gebracht werden kann. P wird
durch Achsenspiegelung an der Achse a auf P' abgebildet.
Eigenschaften Achsenspiegelung
• Die Strecke [PP'] wird durch die Symmetrieachse senkrecht halbiert.
•
Zueinander achsensymmetrische Winkel sind gleich gross, aber
entgegengesetzt orientiert.
•
Zueinander achsensymmetrische Strecken sind gleich lang.
•
Geraden werden auf Geraden und Kreis auf Kreis abgebildet.
3.1.2 Drehsymmetrie
Eine Figur heisst drehsymmetrisch, wenn sie durch Drehung um einen Punkt
um einen von 360°verschiedenen Winkel mit sich selbst zur Deckung gebracht
werden kann. Bei der Drehsymmetrie unterscheidet man zwischen 2 (3, 4, 5,...)
zähliger Drehsymmetrie, je nachdem, ob eine Halb-, (Drittel-, Viertel-,...) Drehung möglich ist.
3.1.3 Punktsymmetrie
Die Punktsymmetrie ist ein Spezialfall der
Drehsymmetrie. Unter Punktsymmetrie versteht man die
2-zählige Drehsymmetrie. Eine geometrische Figur heisst
punksymmetrisch, wenn sie durch eine Drehung von 180°
um einen Punkt Z (Symmetriezentrum) mit sich selbst zur Deckung gebracht
werden kann. P wird durch Punktspiegelung am Zentrum Z auf P' abgebildet.
Eigenschaften Punktspiegelung
• Die Strecke [PP'] wird durch das Symmetriezentrum halbiert.
•
Zueinander punktsymmetrisch Winkel sind gleich gross und
gleichsinnig orientiert.
•
Zueinander punktsymmetrische Strecken sind gleich lang.
•
Geraden werden auf Geraden und Kreise auf Kreise abgebildet.
3.1.4 Schubsymmetrie
Eine Figur heisst schubsymmetrisch, wenn jeder ihrer Punkte durch eine
Verschiebung mit sich selbst zur Deckung kommt.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
35
Berechnungen von Dreieck und Viereck
DialogMathe
3.2 Übersicht Vierecke
Bestimmungsstücke
Ein Viereck wird im Allgemeinen eindeutig bestimmt, wenn von den vier
Seiten und vier Winkeln fünf Stücke gegeben sind. Ein Dreieck erfordert drei
Stücke, für den vierten Eckpunkt des Vierecks benötigt man zwei weitere. Hat
das Viereck spezielle Eigenschaften, so vermindert sich die Anzahl bis auf 1
beim Quadrat.
Symmetrie
Das symmetrische Drachenviereck hat eine Symmetrieachse und das
Parallelegramm ein Symmetriezentrum. Beide liegen deshalb in einer Zeile.
Dann liegen Raute und Rechteck nebeneinander. Beide haben zwei
aufeinander senkrecht stehende Symmetrieachsen und ein
Symmetriezentrum. Das Quadrat hat vier Achsen. Das Trapez passt nicht in
diese Anordnung. (Das gleichschenklige Trapetz hat eine Symmetrieachse).
36
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Übersicht Vierecke
DialogMathe
3.2.1 Quadrat
Definierende Eigenschaft
α = β = γ = δ = 900
a =b =c =d
Flächeninhalt und Umfang
A = a2 ;
U = 4a
Diagonalen
e = f = 2 ⋅a ; e ⊥ f
e und f halbieren einander
weitere Eigenschaften: vier Symmetrieachsen, Punktsymmetrie zu S
3.2.2 Rechteck
Definierende Eigenschaft
α = β = γ = δ = 900
Flächeninhalt und Umfang
A = a ⋅b
U = 2 ⋅ (a + b )
Diagonalen
e = f , e und f halbieren einander
weitere Eigenschaften
a = c und b = d , zwei Symmetrieachsen, Punktsymmetrie zu S
3.2.3 Raute (Rhombus)
Definierende Eigenschaft
a =b =c =d
Flächeninhalt und Umfang
A = 21 ⋅ e ⋅ f ; U = 4a
Diagonalen
e ⊥ f , e und f halbieren einander
weitere Eigenschaften
α = γ und β = δ , Punktsymmetrie zu S
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
37
Berechnungen von Dreieck und Viereck
DialogMathe
3.2.4 Parallelogramm
Definierende Eigenschaft
a c und b d
Flächeninhalt und Umfang
A = a ⋅ ha = b ⋅ hb
U = 2 ⋅ (a + b )
Diagonalen
e und f halbieren einander
weitere Eigenschaften: α = γ und β = δ , a = c und b = d
Benachbarte Winkel haben die Summe 1800 , Punktsymmetrie zu S
3.2.5 Drachenviereck
Definierende Eigenschaft
Eine Diagonale ist Symmetrieachse
Flächeninhalt und Umfang
A = 21 ⋅ e ⋅ f
U = 2 ⋅ (a + b )
Diagonalen
e ⊥ f , eine Diagonale wird halbiert
weitere Eigenschaften: a = d und b = c
3.2.6 Trapez
Definierende Eigenschaft
Mindestens zwei Seiten sind parallel
Flächeninhalt und Umfang
A = 21 ⋅ ( a + c ) ⋅ h = m ⋅ h
U=a+b+c+d
Diagonalen
Nichts Spezielles
weitere Eigenschaften
α + δ = 1800 ; β + γ = 1800
38
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Übersicht Vierecke
DialogMathe
3.2.7 Partnerinterview Vierecke
Partnerinterview Vierecke
Zeit: 15 Minuten
Löse den Multiple – Choice Test (Es sind mehrere Antworten pro Aufgabenstellung möglich). Diskutiere deine Ergebnisse mit deinem Lern-Partner. Falls
Fragen oder Unklarheiten auftauchen, notiere sie! Die Lösungen befinden sich
am Ende des Tests.
Multiple – Choice – Test Vierecke
1) Die Summe der Winkel im Viereck beträgt ...
B) 2700
C) Das Doppelte der Winkelsumme im Dreieck.
A) 1800
0
0
D) 360
E) 90
2) Ein allgemeines Trapez ...
A) hat zwei parallele Seiten.
B) hat vier gleich lange Seiten.
C) hat zwei gleich lange Diagonalen.
D) ist achsensymmetrisch
3) Gegenüberliegende Winkel sind gleich gross ...
A) beim Quadrat
B) beim Rechteck
C) beim Drachen
D) beim gleichschenkligen Trapez
E) bei der Raute
4) Ein Quadrat ist auch ...
A) ein Parallelogramm, dessen Diagonalen senkrecht aufeinander stehen.
B) ein Rechteck mit gleich langen Seiten.
C) eine Raute mit vier rechten Winkeln.
D) ein Trapez mit vier rechten Winkeln.
5) Welche Vierecke haben mindestens zwei Symmetrieachsen?
A) Drachen
B) Parallelogramm
C) Raute
D) Rechteck
E) Quadrat
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
39
Berechnungen von Dreieck und Viereck
DialogMathe
6) Welche Aussagen treffen zu?
A) Jedes Viereck hat mindestens zwei parallele Seiten.
B) Jedes Viereck lässt sich in zwei Dreiecke zerlegen.
C) Die Winkelsumme beträgt immer 360°.
D) Diagonalen liegen immer senkrecht zueinander.
E) Jedes Viereck hat genau zwei Diagonalen.
7) Was macht ein Viereck zu einem allgemeinen Trapez?
A) zwei senkrecht zueinander liegende Seiten
B) zwei gleich lange Seiten
C) zwei gleich grosse Winkel
D) zwei gleich lange Diagonalen
E) zwei parallele Seiten
8) Es gibt nur eine Symmetrieachse ...
A) beim gleichschenkligen Trapez
B) beim Rechteck
C) beim Quadrat
D) beim Drachen
E) beim Parallelogramm
9) Benachbarte Winkel sind immer 180° gross ...
A) beim Drachen
B) beim Trapez
C) beim Parallelogramm
D) beim Quadrat
E) beim Rechteck
10) Für jede Raute gilt:
A) Jede Raute ist auch ein Trapez.
B) Jede Raute ist auch ein Parallelogramm.
C) Jede Raute ist auch ein Drachen.
D) Jede Raute ist auch ein Rechteck
Lösungen: Multiple – Choice – Test Vierecke
1)
2)
3)
4)
5)
40
C, D
A
A,B,E
B,C
C,D,E
6) B,C,E
7) E
8) A, D
9) C,D,E
10) A,B,C
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Strecken – und Flächenberechnungen
DialogMathe
3.3 Strecken – und Flächenberechnungen
3.3.1 Dreiecksfläche und Heron
Grundformel Dreiecksfläche
A ∆ = 21 ⋅ Grundlinie ⋅ Höhe
A ∆ = 21 ⋅ a ⋅ ha
Heron’sche Flächenformel
A∆ =
s⋅(s − a)⋅(s − b)⋅(s − c)
Wobei a, b und c die Längen der Dreiecksseiten sind und s der halbe Umfang.
s=
1
2
⋅(a + b + c)
3.3.2 Berechnungen von Strecken über Flächen
Beispiel 1
Anwendung zur Heron‘schen Flächenformel
Berechne die Dreieckshöhe ha , wenn die Seiten a = 21cm , b = 10 cm und
c = 17 cm gegeben sind.
A ∆ = 21 ⋅ a ⋅ ha
s=
1
2
A∆ =
ha =
Beispiel 2
→
⋅(a + b + c) =
ha =
1
2
2 ⋅ A∆
a
⋅ ( 21 + 10 + 17 ) = 24
s⋅(s − a)⋅(s − b)⋅(s − c) =
24 ⋅ 3 ⋅ 14 ⋅ 7 =
2 ⋅ 4 ⋅ 3 ⋅ 3 ⋅ 2 ⋅ 7 ⋅ 7 = 84
2 ⋅ A ∆ 2 ⋅ 84
=
= 8cm
a
21
Abstand im Quadrat
Gegeben ist das Quadrat ABCD mit der
Seitenlänge a = 4 cm . BP = 1cm ,
M1 und M2 sind Seitenmitten.
Berechne den Abstand x von P zur Strecke M1M2 .
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
41
Berechnungen von Dreieck und Viereck
DialogMathe
Lösungsidee: x als Höhe des Dreiecks ∆PM1M2
berechnen.
A ∆ = A Quadrat − A1 − A 2 − A 3
= 16 − 2 − 3 − 6 = 5
M1M2 = 2 ⋅ 2 (Diagonale des Quadrates mit der
Seitenlänge 2)
x=
2 ⋅ A∆
M1M2
=
2⋅5
5
5⋅ 2
=
=
= 3,54
2
2⋅ 2
2
Nenner wurzelfrei machen
Beachte die Umformung:
5
5⋅ 2
.
=
2
2
Wir erweitern den Bruch
5
mit
2
2:
5⋅ 2
5⋅ 2
.
=
2
2⋅ 2
Warum machen wir diese Umformung?
Da
2 eine irrationale Zahl ist, können wir uns eine Teilung durch
2 nur
schwer vorstellen! Daher macht es Sinn generell Wurzeln im Nenner durch
Erweitern wegzuschaffen.
Teilen im Alltag: Du hast sicher schon einen Apfel halbiert oder in vier Teile
geteilt. Was würdest du machen, wenn du einen Apfel in
2 Teile teilen
müsstest?
Aufgabe
Das Quadrat ABCD hat die Seitenlänge 6cm.
M ist der Mittelpunkt der Quadratseite.
Berechne die schraffierte Dreiecksfläche, wenn
die Dreiecke AEM und BCE flächengleich sind.
[Lösung: A = 15cm 2 ]
42
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
CAS - Bausteine
DialogMathe
3.4 CAS - Bausteine
3.4.1
Rechner - Einsatz: CAS-Bausteine
(CAS = Computer-Algebra-System)
Die mühsame Berechnungsarbeit bei der Anwendung der Heron’schen
Flächenformel, kann mit dem Rechner automatiesiert werden.
Wir definieren einen CAS-Baustein heron(a,b,c):
Der CAS-Baustein h a ( a,b, c ) berechnet aus den Seiten eines Dreiecks die
Höhe. Beachte, dass die entsprechende Höhe h a ( a,… ,… ) durch die Eingabe
der ersten Seite festgelegt wird!
3.4.2
Arbeiten mit „CAS-Bausteinen“
Ein CAS-Baustein ist eine eindeutige Zuordung (siehe später Funktion).
Der Baustein heron(a,b,c) ordnet den drei Seiten a,b,c eines Dreiecks die
Fläche zu. Bausteine sind eine sinnvolle Anwendung, wenn es darum geht,
ein Problem schnell und immer wieder zu lösen. Da der Baustein vom
Benutzer selbst erarbeitet werden muss und der Baustein in der Regel eine
allgemeine Lösung ist (Baustein mit Variablen), ist es eine wunderschöne
Übung, um allgemeine Lösungsansätze herauszufinden. Mit einem Baustein
lässt es sich auch wunderbar experimentieren.
TI-Nspire: Bibliotheken
Eine Bibliothek ist ein TI-Nspire-Dokument, dessen Daten allen andern
Dokumenten zur Verfügung stehen. Objekte einer Bibliothek sind global zum
gesamten Nspire System, während normale Objekte lokal innerhalb eines
Problems sind. Bibliotheken lassen sich im Programmeditor erstellen.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
43
Berechnungen von Dreieck und Viereck
DialogMathe
Arbeiten mit dem Programmeditor von TI-Nspire
Programme werden in der Applikation Calculator erstellt. TI-Nspire verfügt
über einen Programmeditor, der über „menu“,9,1,1 gestartet wird. Gib im
sich öffnenden Fenster den Programmnamen „heron“ ein, als Typ Program
und für Bibliothekszugriff Lib Pub (im Katalog anzeigen).
Mit „OK“ öffnet sich eine geteilte Seite. Im rechten Fenster erscheint das
Programmgerüst unseres Programms. Mit „doc“,5,1 kann das rechte Fenster
verbreitert werden. Die Begrenzung wird mit den Pfeiltasten verschoben.
heron(a,b,c): Das Programm benötigt die drei Seiten des Dreiecks als Eingabe.
a,b,c,s und fläche werden als lokale Variablen definiert. Dann wird der halbe
Umfang s und die Fläche berechnet. Zuletzt wird die Fläche ausgegeben.
Der Stern (*heron) weist darauf hin, dass das Programm noch nicht gespeichert ist. Mit „menu“,2,1 kann die Syntax des Programms geprüft und das
44
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
CAS - Bausteine
DialogMathe
Programm als Variable gespeichert werden. Ist das Programm fehlerfrei, erscheint die Meldung „heron“ erfolgreich gespeichert.
Das Programm kann nun mit „Var“ als Variable „heron“ im Calculator (linke
Seite) aufgerufen werden. Dazu kann mit „doc“,5,1 das linke Fenster wieder
verbreitert werden. Um das Programm in allen Anwendungen zur Verfügung zu haben, muss es mit „Save“ in den Ordner MyLib gespeichert werden.
Gib als File Name „program“ ein (den File Name kannst du wählen! ).
Bevor die Variable „heron“ im Dokument „program“ mittels Katalog aufgerufen werden kann, muss mit „Doc“, 6 die Bibliothek aktualisiert werden.
Beachte: „heron“ ist nun eine Variable im Dokument „program“ und kann
über den Katalog in allen TI-Nspire Dokumenten aufgerufen werden.
Es können weitere Programme als Probleme ins Dokument „program“ geschrieben werden (maximal 30). Verlasse das Dokument „program“ und öffne
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
45
Berechnungen von Dreieck und Viereck
DialogMathe
ein neues. Wähle die Applikation Calculator. Unser Programm kann im Katalog im Register 6 durch „anklicken“ aufgerufen werden. Mit „menu“,1,7,3
kann für „program“ ein shortcut z.B. „p“definiert werden. Gib p. (p Punkt)
ein und es erscheint eine Liste aller Programme im Dokument „program“.
Partnerinterview: Erstellen von CAS-Bausteinen
Zeit: 15 Minuten
Überlege, wo dir die Anwendung von CAS-Bausteinen Vorteile bringen kann.
Erstelle einige nützliche CAS-Bausteine in der Mathematik oder in den
Naturwissenschaften.
CAS-Bausteine in der Mathematik
CAS-Bausteine in der Physik
CAS-Bausteine in der Chemie
46
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Dreieck und Viereck
DialogMathe
3.5 Geometrische Denkaufgaben Dreieck und Viereck
3.5.1
Übungsbeispiele Dreieck und Viereck
Aufgabe 1
Aufgabe 2
M = Mittelpunkt
Aufgabe 3
Aufgabe 4
Lösungen A1: x = 6 cm
A3: x = 12cm
A2: A 1 = 6 cm2 , A 2 = 20 cm2 , A3 = 14cm2
A4: x + y = 25 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
47
Berechnungen von Dreieck und Viereck
Aufgabe 5
DialogMathe
M = Mittelpunkt
Aufgabe 6
Aufgabe 7
Aufgabe 8
Lösungen
48
A5: 38
A6: x = 18 cm
A7: x = 20 cm
A8: x = 45 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Dreieck und Viereck
DialogMathe
Aufgabe 9
Aufgabe 10
Aufgabe 11
Aufgabe 12
Lösungen
A9: A = 28 cm2
A10: A = 28 cm2
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A11: A = 9 cm 2
A12: D = 15 cm2
49
Berechnungen von Dreieck und Viereck
DialogMathe
3.5.2 Repetitionstest Dreieck und Viereck
Repetitionstest: Dreieck und Viereck
Zeit: 45 Minuten
Aufgabe 1
M = Mittelpunkt
Aufgabe 2
Aufgabe 3
50
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Dreieck und Viereck
DialogMathe
Aufgabe 4
Aufgabe 5
Aufgabe 6
Lösungen
A1: x = 8 cm
A2: x = 4 cm
A5: x = 9 cm
A6: A = 26 cm2
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A3: A = 240 cm2
A4: x = 6 cm
51
Berechnungen am rechtwinkligen Dreieck
DialogMathe
4 Berechnungen am rechtwinkligen Dreieck
Bezeichnungen
a, b : Katheten
;
c : Hypotenuse
h : Höhe
;
p, q : Hypotenusenabschnitte
4.1 Sätze am rechtwinkligen Dreieck
Pythagoras : c 2 = a2 + b2
Höhensatz: h2 = p ⋅ q
Kathetensatz: a2 = p ⋅ c , b2 = q ⋅ c
4.1.1
Beweis Satz von Pythagoras
Partnerinterview: Beweis Satz von Pythagoras
Zeit: 15 Minuten
Für den Satz von Pythagoras gibt es zahlreiche Beweise!
Entwickle eine Idee, für einen Beweis des Satzes von Pythagoras.
Suche einen Beweis im Internet!
52
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
/ Sätze am rechtwinkligen Dreieck
DialogMathe
Beweis: Satz von Pythagoras
4.1.2 Beweis Höhensatz, Kathetensatz
Mit Hilfe des Satzes von Pythagoras lassen sich der Höhen- und Kathetensatz
rein algebraisch beweisen: Betrachte die beiden rechtwinkligen Teildreiecke
AFC und FBC (siehe Figur Seite 50).
Pythagoras: b2 = q2 + h2 und a2 = p2 + h2
Addiere die beiden Gleichungen: a2 + b2 = p2 + q2 + 2h2
Mit a 2 + b2 = c 2 = ( p + q )2 = p2 + 2pq + q2 erhalten wir
a 2 + b2 = c 2 = ( p + q ) = p2 + 2pq + q2 und damit
2
p2 + 2pq + q2 = p2 + q2 + 2h2
→
2pq = 2h2
→
h2 = pq
Kathetensatz: a2 = p2 + h2 = p2 + pq = p ( p + q ) = pc . Die beiden Sätze lassen
sich auch mit Hilfe der Ähnlichkeit beweisen (siehe Kap. 6.1.2 Seite 91)
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
53
Berechnungen am rechtwinkligen Dreieck
DialogMathe
4.2 Geometrische Denkaufgaben Pythagoras
4.2.1
Übungsbeispiele Pythagoras
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Lösungen A1: x = 10 cm
54
A2: A = 2100 / x + y + z = 240
A3: x = 17 cm
A4: x = 14 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Pythagoras
DialogMathe
Aufgabe 5
Aufgabe 6
Aufgabe 7
Aufgabe 8
Lösungen
A5: x = 4 cm
A6: x = 30 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A7: x = 26 cm
A8: A = 98 cm2
55
Berechnungen am rechtwinkligen Dreieck
DialogMathe
Aufgabe 9
Aufgabe 10
Aufgabe 11
Lösungen
56
A9: x = 13 cm
A10: x = 13 cm
A11: x = 6 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Pythagoras
DialogMathe
4.2.2 Repetitionstest Pythagoras
Repetitionstest: Pythagoras
Zeit: 45 Minuten
Löse die 5 Aufgaben ohne Hilfsmittel als Test.
Simuliere eine Prüfungssituation, arbeite mit einer Uhr. Zeit für eine Augabe
ca. 9 Minuten. Falls dir der Zugang zu einer Aufgabe innerhalb nützlicher
Frist nicht gelingt, überspringe sie.
Ziel: In der vorgegebenen Zeit möglichst viele gelöste Aufgaben!
Aufgabe 1
Aufgabe 2
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
57
Berechnungen am rechtwinkligen Dreieck
DialogMathe
Aufgabe 3
Aufgabe 4
Aufgabe 5
Lösungen A1: x = 28 cm
58
A2: x = 8 cm
A3: x = 7 cm
A4: x = 10 cm
A5: x = 74 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Pythagoras
DialogMathe
4.2.3 Berechnungsaufgaben mit Parametern
Aufgabe 1: Drücke x durch a aus.
Aufgabe 2: Berechne x aus a.
Aufgabe 3: Berechne den Abstand x der Ecke B von der Geraden AE,
ausgedrückt durch a.
Lösungen Berechnungsaufgaben mit Parametern
Aufgabe 1: x =
10 ⋅ a ≈ 3,16a
5
⋅ a ≈ 0,745a
3
30
Aufgabe 3: x =
⋅ a ≈ 5,14a
34
Aufgabe 2: x =
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
59
Berechnungen am rechtwinkligen Dreieck
DialogMathe
4.3 Spezielle rechtwinklige Dreiecke
4.3.1 Memo: Spezielle rechtwinklige Dreiecke
Memo
Spezielle rechtwinklige Dreiecke
900 − 450 − 450 − Dreieck / 900 − 600 − 300 − Dreieck
Das gleichschenklig rechtwinklige Dreieck ( 900 − 450 − 450 − Dreieck ) → halbes Quadrat !
AB = BC = s
AC = d =
2 ⋅s
(Diagonale)
Die Hypotenuse ist
2 mal die Kathete!
Pythagoras: d 2 = s2 + s2
d 2 = 2s2
d=
2s2 =
2 ⋅s
s=
d
2
=
⋅d
2
2
Das 900 − 600 − 300 − Dreieck → halbes gleichseitiges Dreieck
AB =
s
; BC = s
2
AC = h =
3
⋅s
2
Die Kathete h ist
(Höhe)
3
mal die Hypotenuse!
2
2
s
Pythagoras: h 2 = s2 −  
2
3
h 2 = ⋅ s2
4
3 2
3
h=
⋅s =
⋅s
4
2
2
2⋅ 3
s=
⋅h =
⋅h
3
3
60
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Spezielle rechtwinklige Dreiecke
DialogMathe
4.3.2 Repetitionstest: Spezielle Dreiecke
Repetitionstest: Spezielle Dreiecke
Zeit: 15 Minuten
Aufgabe 1
Gegeben: Gleichschenkliges
Dreieck ABC (a = b), Seite c
Gesucht: Seite a und Höhe h
Aufgabe 2
Gegeben: z
Gesucht: x und y
Aufgabe 3
Gegeben: Gleichseitiges Dreieck mit der Seitenlänge s.
Gesucht: Fläche des Dreiecks.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
61
Berechnungen am rechtwinkligen Dreieck
DialogMathe
4.3.3 Aufgaben: Spezielle Dreiecke
Aufgabe 1
Das rechtwinklige Dreieck ACD ist
gleichschenklig CD = AD .
Berechne die Fläche des Vierecks ABCD,
wenn die Seite AB =
2 ist. (Lösung exakt
angeben, d.h. nicht aufgehende Wurzeln
stehen lassen)
Aufgabe 2
Berechne die Fläche des Trapezes
ABCD aus DC = s .
Aufgabe 3
Die Geraden a und b sind Tangenten
an den Kreis.
Berechne aus h = 10 cm den Radius r
des Kreises.
Aufgabe 4
Das Dreieck ABC ist gleichseitig
und hat die Seitenlänge c = 5.
Berechne den Inhalt der
schraffierten Fläche BDEF.
62
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Spezielle rechtwinklige Dreiecke
DialogMathe
Aufgabe 5
In der nebenstehenden Figur ist D der
Schnittpunkt der Winkelhalbierenden
des Winkels ∢BCA = 600 mit dem
Umkreis des Dreiecks ABC.
Berechne den Flächeninhalt des
Dreiecks ABD aus der Länge c der
Seite AB
4.3.4 Lösungen Spezielle Dreiecke
Repetitionstest: Spezielle Dreiecke
c
2 ⋅c
=
2
2
c
h=
2
2
2⋅ 3
Aufgabe 2: x =
⋅z =
⋅z
3
3
3 2
Aufgabe 3: A =
⋅s
4
Aufgabe 1: a =
Aufgaben: Spezielle Dreiecke
Aufgabe 1: A = 32 +
1
3
Aufgabe 2:  +
2
12

3
 2
⋅s

Aufgabe 3: r = 20 ⋅ 3
Aufgabe 4: A schraffiert = 0,125 c 2 = 3,125
Aufgabe 5: A =
c2
4⋅ 3
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
63
Berechnungen am rechtwinkligen Dreieck
DialogMathe
4.4 Pythagoras und Kreisberührungen
Memos
Pythagoras und Kreisberührungen
Merke
Bei einer Berührung von zwei Kreisen k1 und k2 liegt der Berührungspunkt B
immer auf der Verbindungslinie M1 M2 der beiden Kreismittelpunkten
M1 und M2.
Für die Berührung von zwei Kreisen k1 und k2 können wir
zwei Fälle unterscheiden:
Äussere Berührung
Innere Berührung
Begründung
Die beiden sich berührenden Kreise k1 und k2 haben eine gemeinsame TanTa
gente t. Der Berührungsradius steht jeweils senkrecht zur Tangente. Damit ere
geben sich bei der äusseren Berührung beim Berührungspunkt B zwei 900
Winkel, d.h. ein gestreckter
gestreck Winkel (1800). Somit liegen die Kreismittelpunkte
M1 und M2 und der Berührungspunkt B auf einer Geraden. Bei der inneren BeB
rührung liegen die Berührungsradien aufeinander.
Wir können drei verschiedene Aufgabentypen (Lösungsideen) unterscheiden.
64
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Pythagoras und Kreisberührungen
DialogMathe
4.4.1 Typ 1: ein rechtwinkliges Dreieck
Berechne r aus b.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
65
Berechnungen am rechtwinkligen Dreieck
DialogMathe
4.4.2 Typ 2: Eine Strecke auf zwei verschiedene Arten berechnen
Berechne r aus a.
Lösungsvariante (Typ 1)
66
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Pythagoras und Kreisberührungen
DialogMathe
4.4.3 Typ 3: zwei rechtwinklige Dreiecke
Berechne r aus b.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
67
Berechnungen am rechtwinkligen Dreieck
DialogMathe
4.4.4 Lösungen der Beispiele Typ 1 , 2 und 3 mit dem Rechner
Interpretiere die Rechnerlösungen
4.4.5 Aufgaben: Kreisberührungen
Aufgabe 1
In einem Viertelkreis befinden sich zwei
Halbkreise, die sich berühren (siehe Figur).
Berechne den Radius x, wenn der Radius r
gegeben ist.
68
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Pythagoras und Kreisberührungen
DialogMathe
Aufgabe 2
Gegeben sei ein Quadrat ABCD mit
der Seitenlänge a. Berechne den
Radius x aus a.
Aufgabe 3
Gegeben ist ein Quadrat mit der
Seitenlänge 3a und ein Kreis mit
Radius a.
Wie gross ist der Radius x des
Halbkreises?
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
69
Berechnungen am rechtwinkligen Dreieck
DialogMathe
Aufgabe 4
Berechne aus der folgenden Figur
den Radius x aus r.
ZA = r ; ZP =
r
4
WZ =
r
2
Aufgabe 5
Gegeben: Rechteck mit den Seiten a
und b.
Gesucht: Radius x des kleinen
Kreises.
70
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Pythagoras und Kreisberührungen
DialogMathe
Aufgabe 6: Kirchenfenster
Berechne x aus r.
4.4.6 Lösungen der Aufgaben 1 bis 6 mit dem Rechner
Interpretiere die Rechnerlösungen!
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
71
Dreieckskonstruktionen
DialogMathe
5 Dreieckskonstruktionen
Kennen wir drei Stücke eines Dreiecks, so lässt es sich konstruieren.
Konstruieren heisst Punkte durch schneiden von geometrischen Örtern zu
bestimmen.
Später in der Trigonometrie werden wir sehen, dass sich ein Dreieck aus drei
gegebenen Stücken vollständig berechnen lässt.
5.1 Geometrische Örter
Geometrische Örter sind Punktmengen, die gewisse Bedingungen erfüllen.
5.1.1 Kreis
Wo liegen alle Punkte P, die von
einem Punkt M den gleichen
Abstand r haben?
5.1.2 Parallelenstreifen
Wo liegen alle Punkte P, die
von einer Geraden g den
gleichen Abstand h haben?
72
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Örter
DialogMathe
5.1.3 Mittelsenkrechte
Wo liegen alle Punkte P, die von
zwei Punkten A und B den
gleichen Abstand haben?
AP = BP
5.1.4 Winkelhalbierende
Wo liegen alle Punkte P, die
von zwei sich schneidenden
Geraden g und h den gleichen
Abstand haben?
5.1.5 Ortsbogen für einen Winkel α
Wo liegen alle Punkte P, von
welchen eine Strecke AB unter
einem beliebigen Winkel
α ∈ ] 0 ; 180 [ erscheint.
5.1.6 Speziell: Thaleskreis
Wo liegen alle Punkte P, von
welchen eine Strecke AB unter
einem rechten Winkel erscheint.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
73
Dreieckskonstruktionen
DialogMathe
5.2 Dreiecksstücke
Seiten a, b, c
Winkel α, β, γ
Höhen ha , hb , hc
Seitenhalbierende sa , sb , sc
Winkelhalbierende w a , w b , w c
Umkreisradius R,
R Inkreisradius r
5.2.1 Partnerinterview spezielle Linien im Dreieck
Partnerinterview spezielle Linien im Dreieck
Zeit: 15 Minuten
1. Höhen
Wie ist eine Höhe im Dreieck definiert?
2. Seitenhalbierende
Wie ist die Seitenhalbierende im Dreieck definiert?
Die drei Seitenhalbierenden in einem Dreieck schneiden sich in einem
Punkt. Wie nennen wir diesen Punkt und welche Eigenschaften hat er?
74
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Dreiecksstücke
DialogMathe
3. Winkelhalbierenden
Wie ist eine Winkelhalbierende im Dreieck definiert? Welche Eigenschaften
besitzen die Punkte auf der Winkelhalbierenden?
Die drei Winkelhalbierenden in einem Dreieck schneiden sich in einem
Punkt. Wie nennen wir diesen Punkt und welche Eigenschaften hat er?
4. Mittelsenkrechten
Wie ist eine Mittelsenkrechte im Dreieck definiert? Welche Eigenschaften
besitzen die Punkte auf der Mittelsenkrechten?
Die drei Mittelsenkrechten in einem Dreieck schneiden sich in einem Punkt.
Wie nennen wir diesen Punkt und welche Eigenschaften hat er?
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
75
Dreieckskonstruktionen
DialogMathe
5.2.2 Der Schwerpunkt eines Dreiecks
Der Schwerpunkt S eines beliebigen Dreiecks teilt jede Schwerelinie
(Seitenhalbierende) im Verhältnis 2 : 1.
5.2.3 Umkreismittelpunkt
Die drei Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt U.
Der Schnittpunkt ist Zentrum des Umkreises.
5.2.4 Inkreismittelpunkt
Die drei Winkelhalbierenden in einem Dreieck schneiden sich in einem Punkt
I. Der Schittpunkt ist Zentrum des Inkreises.
76
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Dreiecksstücke
DialogMathe
5.2.5 Die Winkelhalbierende im Dreieck
In jedem Dreieck gilt: Eine Winkelhalbierende ( w γ ) teilt die Gegenseite (c) im
Verhältnis der anliegenden Seiten.
u
a
=
v
b
5.2.6 Anwendungen Winkelhalbierende: Berechnungsaufgaben
Aufgabe 1
Berechne die Fläche A des rechtwinkligen Dreiecks ABC.
(w = CE = Winkelhalbierende)
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
77
Dreieckskonstruktionen
DialogMathe
Aufgabe 2
Berechne die schraffierte Fläche A. (w = BE = Winkelhalbierende)
Aufgabe 3
Strahlensatz, siehe Kap. 6.2 Seite 94
(w = Winkelhalbierende)
Lösungen
78
A1: A = 294 cm2
A 2: A = 54 cm2
A3: x = 60 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Dreiecksstücke
DialogMathe
5.2.7 Tangentenabschnitte
Die Tangentenabschnitte sind gleich lang: a1 = a2
(Die Dreiecke ∆PMB1 und ∆PMB2 sind deckungsgleich.)
Anwendung
Lösungen
x = 15 cm
Tangentenviereck
Vierecke, die einen Inkreis besitzen.
Zeige: Es gilt a + c = b + d .
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
79
Dreieckskonstruktionen
DialogMathe
5.2.8 Dynamisches Geometrieprogramm von TI-Nspire
Mit Hilfe von TI-Nspire lassen sich geometrische Sachverhalte dynamisch
veranschaulichen. Im Folgenden einige Beispiele:
Beispiel 1: Umkreismittelpunkt
Dreieck ABC zeichnen und die Mittelsenkrechten konstruieren. Diese
schneiden sich in einem Punkt U, dem Umkreismittelpunkt.
Nun können wir die Form des Dreiecks verändern und dabei die Lage von U
beobachten.
Spizwinkliges Dreieck
Umkreismittelpunkt U
liegt im Innern des
Dreiecks!
Rechtwinkliges Dreieck
Umkreismittelpunkt U
liegt auf der Hypotenuse
Stumpfwinkliges Dreieck
Umkreismittelpunkt U
liegt ausserhalb des
Dreiecks
80
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Dreiecksstücke
DialogMathe
Beispiel 2: Teilverhältnis der Winkelhalbierenden
Dreieck ABC zeichnen und eine Winkelhalbierende konstruieren.
Die Dreiecksseiten b und c , sowie die beiden Teilabschnitte u und v können
gemessen werden und damit die beiden Verhältnisse berechnet werden.
Analog lassen sich andere Eigenschaften im Dreieck veranschaulichen., z.B.,
Lage des Höhenschnittpunkts
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Teilverhältnis Seitenhalbierende
81
Dreieckskonstruktionen
5.3
DialogMathe
Konstruktionsbeschreibung
Ein Dreieck konstruieren heisst die drei Eckpunkte des Dreiecks bestimmen.
Die Eckpunkte erhalten wir durch schneiden von geometrischen Örtern.
Im folgenden wollen wir Dreiecke nicht mit Zirkel und Lineal konstruieren,
sondern mit Hilfe einer Schaufigur und einer Konstruktionsbeschreibung.
Diese soll sich auf die Schaufigur beziehen und in einer mathematischen
Sprache kompakt und verständlich die einzelnen Schritte der Konstruktion
wiedergeben.
5.3.1 Musterbeispiele
Beispiel 1
Gegeben: α, a, ha
KB (Konstruktionsbeschreibung):
1) Höhenstreifen ha → p, q
2) a auf p hinlegen → B, C
3) Ortsbogen für α über BC ∩ q → A
Kommentar
Schritt 1: Höhenstreifen ha → p, q
Auf q liegt der Punkt A, q ist der 1. geometrische Ort für die Ecke A.
p ist der 1. geometrische Ort für die Ecke B und C
Schritt 2: a auf p hinlegen → B, C
Schritt 3: Ortsbogen für α über BC ∩ q → A
Der Ortsbogen ist der 2. geometrischer Ort für A.
Die Ecke A ergibt sich als Schnittpunkt der beiden geometrischen Örter.
82
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Konstruktionsbeschreibung
DialogMathe
Beispiel 2
Gegeben: α, ha , hb
KB.
1) Teildreieck ABFb ( hb , α, 900 )
2) Thaleskreis über AB ∩ Kreis ( A,r = ha ) → Fa
3) BFa ∩ AFb → C
Oder
1) Höhenstreifen hb → p, q
2) A auf p wählen → A
3) Winkel α bei A an p antragen → AB
4) AB ∩ q → B
5) Thaleskreis über AB ∩ q → Fa
6) BFa ∩ p → C
Beispiel 3
Gegeben: β, γ, sa
KB.
Lösungsidee: B und C sind Punktsymmetrisch
1) sa hinlegen → A, Ma
2) Ortsbogen für β über AMa spiegeln an Ma → Ortsbogen∗
3) Ortsbogen für γ über AMa ∩ Ortsbogen∗ → C
4) C an Ma spiegeln → B
Oder
1) Ähnliches Dreieck AB 'C' mit β, γ, sa '
s
2) Zentrische Streckung  Strekungszentrum A,Streckungsfaktor z = a 
s

a'
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
83
Dreieckskonstruktionen
Beispiel 4
DialogMathe
Gegeben: sa , sb , γ
KB.
1) 2sb hinlegen → B, D
2) Kreis ( Mb ,r = 31 sb ) ∩ MbB → S
3) Kreis ( S,r = 32 sa ) ∩ Ortsbogen für γ über DMb → A
4) A an Mb spiege ln → C
Oder
1) sa hinlegen → A, Ma
2) Kreis ( A,r = 23 sa ) ∩ AMa → S
3) Ortsbogen für γ über AMa an Ma spiege ln → Ortsbogen∗
4) Kreis ( S,r = 32 sb ) ∩ Ortsbogen∗ → B
5) B an Ma spiegeln → C
5.3.2 Übungsbeispiele Dreieckskonstruktionen
Übung 1 Gegeben: b, c, ha
84
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
DialogMathe
Konstruktionsbeschreibung
Übung 2 Gegeben: β, γ, ha
Übung 3 Gegeben: a, ha , hb
Übung 4 Gegeben: a, sa , α
Übung 5 Gegeben: c, sa , γ
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
85
Dreieckskonstruktionen
DialogMathe
Übung 6 Gegeben: a, sa , sb
Übung 7 Gegeben: b, ha , sb
Übung 8 Gegeben: w α , hb , α
Übung 9 Gegeben: r, ha , α
86
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Konstruktionsbeschreibung
DialogMathe
Übung 10
Gegeben: R, ha , α
5.3.3 Partnerinterview Lösungsideen für Dreieckskonstruktionen
Partnerinterview Lösungsideen für Dreieckskonstruktionen
Zeit: 20 Minuten
Fasse die wichtigsten Lösungsideen für die Dreieckskonstruktionen
zusammen und diskutiere sie! Höhenstreifen, Ortsbogen, Teildreieck,
Symmetrie, Ähnlichkeit, Parallelogramm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
87
Streckenverhältnisse
DialogMathe
6 Streckenverhältnisse
Wir haben schon zwei wichtige Sätze kennengelernt, in denen
Streckenverhältnisse vorkommen.
1. Der Schwerpunkt teilt die Seitenhalbierende im Verhältnis 2:1.
2. Die Winkelhalbierende teilt die gegenüberleigende Seite im Verhältnis
der anliegenden Seiten.
Hier handelt es sich um Teilungsverhältnisse. Im Folgenden wollen wir die
Seitenverhältnisse von ähnlichen (formgleichen) Dreiecken betrachten.
Du kennst den wichtigen Begriff kongruente (deckungsgleiche) Dreiecke.
Dreiecke, die deckungsgleich sind, besitzen den gleichen Flächeninhalt und
die gleiche Form. (deckungsgleich = flächengleich + formgleich)
Flächengleichheit
Berechnung der Dreiecksfläche: A =
g ⋅ h Grundlinie mal Höhe
=
2
2
Begründe: Die Dreiecke ∆ABC , ∆ABC1 , ∆ABC2 und ∆ABC3 haben die
gleiche Fläche.
Formgleichheit
Wann sind Dreiecke formgleich?
88
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Ähnliche Dreiecke
DialogMathe
Bei kongruenten (deckungsgleichen) Dreiecken sind zwei entsprechende
Strecken (z.B. Seiten, Höhen usw.) gleich. Bei ähnlichen (formgleichen)
Dreiecken ist das Verhältis von zwei entsprechenden Strecken gleich.
Durch Gleichsetzen von Streckenverhältnissen ähnlicher Figuren erhalten wir
Gleichungen, aus denen jeweils eine Strecke berechnet werden kann. Dies
wollen wir im Kapitel 6.1 für Dreiecke anwenden.
Bei ähnlichen Dreiecken in perspektivischer Lage (zentrische Streckung)
kennen wir die Strahlensätze (Kap. 6.2), die uns bei Streckenberechnungen
helfen können.
Speziell untersuchen wir in Kap. 7.3 den Zusammenhang zwischen Winkel
und Seitenverhältnissen von ähnlichen rechtwinkligen Dreiecken. Wir
definieren Zuordungen (trigonometrische Funktionen) bei denen einem
Seitenverhältnis ein Winkel zugeordnet wird. Mit diesem Werkzeug lassen
sich Dreiecksberechnungen durchführen.
6.1 Ähnliche Dreiecke
Stimmen zwei Dreiecke in zwei Winkeln überein, dann sind sie ähnlich.
α = α ' und β = β '
⇒
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
∆ABC ∼ ∆A 'B ' C '
89
Streckenverhältnisse
DialogMathe
6.1.1 Partnerinterview ähnliche Dreiecke
Partnerinterview ähnliche Dreiecke
Zeit: 20 Minuten
Finde alle ähnlichen Dreiecke und beweise deren Ähnlichkeit.
Beispiel 1
Beispiel 2
Beispiel 3
90
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Ähnliche Dreiecke
DialogMathe
Berechnungen mit Ähnlichkeit
Wenn zwei Dreiecke ähnlich sind, dann haben zwei entsprechende Strecken
(z.B. Seiten, Höhen, Winkelhalbierende, Umkreisradien, Umfänge . . . . ) das
gleiche Längenverhältnis.
∆ABC ∼ ∆A 'B ' C '
⇒
k=
a ' h ' w ' R ' U'
=
=
=
=
a
h
w
R
U
6.1.2 Partnerinterview Berechnungen mit Ähnlichkeit
Partnerinterview Berechnungen mit Ähnlichkeit
Zeit: 10 Minuten
Zeige mit Hilfe ähnlicher Dreiecke, dass die folgenden Sätze am rechtwinkligen Dreieck gelten.
Höhensatz: h2 = p ⋅ q
Die beiden ähnlichen Dreiecke:
Seitenverhältnis:
Kathetensatz: a2 = p ⋅ c
Die beiden ähnlichen Dreiecke:
Seitenverhältnis:
Kathetensatz: b2 = q ⋅ c
Die beiden ähnlichen Dreiecke:
Seitenverhältnis:
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
91
Streckenverhältnisse
DialogMathe
Flächeninhalte ähnlicher Dreiecke
Die Flächeninhalte ähnlicher Dreiecke verhalten sich wie die Quadrate
entsprechender Strecken.
∆ABC ∼ ∆A 'B ' C '
⇒
A A 'B 'C '
= k2
A ABC
2
A A 'B 'C ' = k 2 ⋅ A ABC
⇒
2
2
a'
h'
w' 
k 2 =   =   = 
 = ⋯⋯
a 
h
 w 
6.1.3 Partnerinterview Flächeninhalte ähnlicher Dreiecke
Partnerinterview Flächeninhalte ähnlicher Dreiecke
Zeit: 10 Minuten
Gegeben ∆ABC ∼ ∆A 'B ' C '
Dreieck ABC: Grundlinie c und Höhe h
Dreieck A’B’C’: Grundlinie c’ = 2c und Höhe h’ = 2h
Streckenverhältnis:
k=
c ' h'
=
=
c
h
Flächenverhältnis:
92
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Ähnliche Dreiecke
DialogMathe
6.1.4 Aufgaben zur Ähnlichkeit
Aufgabe 1
Berechne im nebenstehenden Dreieck ABC die Seite AC = x , wenn BC = 5cm
und BD = 3cm gegeben sind.
Aufgabe 2
Für die Flächen der Dreiecke ASD und BCS gilt:
A ∆ASD
225
=
A ∆BCS
49
a) Zeige, dass die Dreiecke ASD und BCS ähnlich sind.
b) Berechne den Radius r = MA = MB des Halbkreises, wenn AD = 12 und
DS = 9 ist.
Lösungen
Aufgabe 1:
x=
Aufgabe 2:
a) Dreiecke haben gleiche Winkel (Thaleskreis, Scheitelwinkel)
b) r = 10
80
9
≈ 8,89
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
93
Streckenverhältnisse
DialogMathe
6.2 Strahlensätze
Eine Strahlensatzfigur besteht aus zwei sich schneidenen Geraden g und h
und zwei parallelen Geraden p und q.
Der Schnittpunkt Z von g und h nennen wir Strahlensatzzentrum.
Die Strecken auf den sich schneidenden Geraden g und h heissen
Strahlenabschnitte.
Die Strecken auf den Parallelen p un q heissen Parallelenabschnitte.
94
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Strahlensätze
DialogMathe
6.2.1 Erster Strahlensatz
Ohne Parallelenabschnitte (c, d) oder (m, n)
nur mit Strahlenabschnitten ( a1,a 2 ,b1,b 2 ) oder ( u1,u2 , v1,v 2 )
a1
b
= 1
a2
b2
oder
u1
v
= 1
u2
v2
a1
b1
=
a1 + a2
b1 + b2
Auch möglich
a1
a
= 2
b1
b2
6.2.2 Zweiter Strahlensatz
Mit Parallelenabschnitten (c,d) oder (m, n) und
mit Strahlenabschnitten ( a1,a 2 ,b1,b 2 ) oder ( u1,u2 , v1,v 2 )
c
a1
=
d
a1 + a2
oder
m
u
= 1
n
u2
c
b1
=
d
b1 + b2
Auch möglich
c
d
=
b1
b1 + b2
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
oder
m
v
= 1
n
v2
Auch möglich
v1
v
= 2
m
n
95
Streckenverhältnisse
DialogMathe
6.2.3 Partnerinterview Berechnungen mit den Strahlensätzen
Partnerinterview Berechnungen mit Strahlensätzen
Zeit: 10 Minuten
Berechnungen ohne Taschenrechner!
1. Strahlensatz : Berechne x und y. (Strahlenabschnitte)
2. Strahlensatz: Berechne x, y und z. (Strahlenabschnitte und
Parallelabschnitte)
Berechne x und die Fläche A1 , wenn A 2 = 4cm2
96
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Strahlensätze
DialogMathe
6.2.4 Aufgaben Strahlensätze
Aufgabe 1 : Geometrie im Garten
In einem Garten stehen zwei Pfähle mit den
Höhen a = 2m und b = 3m im Abstand d = 5m.
Jede Pfahlspitze ist mit dem Fuss des andern
Pfahles durch eine gespannte Schnur verbunden.
a) In welcher Höhe h treffen sich die Schnüre?
b) Wie ändert sich die Höhe h, wenn der Abstand d halbiert wird?
Aufgabe 2
Gegeben: Quadrat ABCD mit der Seite s = 10 cm ; FA = 2s
M = Mitte von BC
Gesucht: Strecke EM = x
Aufgabe 3
Gegeben:
rechtwinkliges Dreieck ABC mit
BC = 6 cm ; AC = 8 cm .
Gesucht: Strecke EF = x
Lösungen Aufgaben Strahlensätze
Aufgabe 1: a) h = 1,2 m b) h bleibt gleich (ist unabhängig von d)
Aufgabe 2: x = 10,14 cm
Aufgabe 3: x = 3,43 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
97
Streckenverhältnisse
DialogMathe
6.3 Geometrische Denkaufgaben Strahlensätze und Ähnlichkeit
6.3.1 Übungsbeispiele Strahlensätze und Ähnlichkeit
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Lösungen
98
A1: A = 27 cm2
A 2: A = 84 cm2
A3: A = 300 cm2
A4: x = 6 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Strahlensätze und Ähnlichkeit
DialogMathe
Aufgabe 5
Aufgabe 6
Aufgabe 7
Aufgabe 8
Lösungen
A5: x = 3 cm
A 6: x = 100 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A7: x = 6 cm
A8: x = 12cm
99
Streckenverhältnisse
DialogMathe
Aufgabe 9
Aufgabe 10
Aufgabe 11
Aufgabe 12
Lösungen
100
A9: x = 24 cm
A 10: x = 35 cm
A11: A = 42cm2
A12: x = 6 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Strahlensätze und Ähnlichkeit
DialogMathe
6.3.2 Repetitionstest Strahlensätze und Ähnlichkeit
Repetitionstest : Strahlensätze und Ähnlichkeit
Zeit: 25 Minuten
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Lösungen
A1: x = 10 cm
A2: A = 864 cm2
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A3: x = 45 cm
A4: A = 42cm2
101
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
7 Algebraische Behandlung von Geometrieaufgaben
7.1 Geometrische Denkaufgaben Lösungen mit dem CAS
Mathematisch arbeiten heisst Gleichungen aufstellen. Beim Lösen von
Problemen können wir Unbekannte einführen. Brauchen wir eine Grösse zur
Berechnung einer anderen und ist diese nicht bekannt, so geben wir ihr einen
Namen. Somit haben wir eine weitere Unbekannte in unser Problem
eingeführt. Die Anzahl der Unbekannten sollte möglichst klein sein, denn für
jede Unbekannte braucht es eine Gleichung, damit diese bestimmt werden
kann. In den Gleichungen, die wir aufstellen können mehrere Unbekannten
vorkommen. Da die Gleichungen miteinander gekoppelt sind, sprechen wir
von einem Gleichungssystem. Ein 2x2 Gleichungssystem besteht aus zwei
Gleichungen, die zwei Unbekannten bestimmen können. Das Auflösen von
Gleichungssystemen ist in der Regel sehr aufwendig (siehe später). Der
Rechner kann uns diese Arbeit mit Hilfe des „solve-Befehles“ abnehmen!
Dadurch gewinnen wir Zeit, vor allem wenn es sich um 3x3 oder grössere
Gleichungssysteme handelt. Jedoch müssen wir die vom Rechner
vorgeschlagene Lösung Interpretieren und auf ihre Richtigkeit überprüfen!
Im folgenden diskutieren wir einige schon gelöste geometrische
Denkaufgaben. Dabei verwenden wir jeweils die folgenden zwei
verschiedenen Lösungsansätze:
•
Algebraische Lösungsmethode (Gleichungssystem)
Wir führen Unbekannte ein und stellen Gleichungen auf. Die
Gleichungen erhalten wir durch Anwenden von geometrischen Sätzen.
Zum Auflösen des Gleichungssystems brauchen wir den Rechner!
•
Geometrische Lösungsmethode (sequentielle Lösung)
Wir berechnen Hilfsgrössen, die zur gesuchten Grösse führen, jeweils
nacheinander. Der Rechner wird nicht benötigt.
102
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Lösungen mit dem CAS
DialogMathe
7.1.1
Aufgabe 1 Seite 101: Vergleich von zwei verschiedenen Lösungen
Algebraische Lösung mit Hilfe von Gleichungen (Gleichungssystem)
Einführung von zwei Unbekannten:
y = DE und z = DB .
Wir brauchen drei Gleichungen für die Unbekannten x, y und z.
1. Strahlensatz Zentrum Punkt A:
12 : y = ( 12 + z ) : 24
2. Bestimmungsgleichung 5D = 4T:
5⋅
3. Pythagoras Dreieck EFC :
12 ⋅ y
y + 24
= 4⋅
⋅z
2
2
x 2 = z 2 + ( 24 − y )
2
Auflösen des Gleichungssystems mit Hilfe des Rechners.
Berechnung von y und z (2x2 – Gleichungssystem), anschliessend Berechnung
von x!
Berechnung von x , y und z (3x3 – Gleichungssystem)
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
103
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
Lösung ohne Rechner (geometrische Lösung mit Hilfe des Ähnlichkeitsfaktors)
Ähnliche Flächen:
→
k=
D
4
= = k2
D+T 9
2
(Ähnlichkeitsfaktor)
3
AE = 2x ; AC = 3x ;
AB =
3
⋅ AD = 18cm
2
Pythagoras im Dreieck ABC: →
7.1.2
3x =
18 2 + 24 2 = 30
→
x = 10cm
Aufgabe 8 Seite 99: Vergleich von zwei verschiedenen Lösungen
Lösung ohne Rechner (geometrische Lösung mit Hilfe des Ähnlichkeitsfaktors)
Hilfslinie M1 M3 , Strahlensatz Zentrum B
GM3 = 5
→
GM1 = 15
Ähnliche Dreiecke: ∆M1GE ∼ ∆CM2E
Ähnlichkeitsfaktors: k =
15 3
=
10 2
M1 E = 3T ; EC = 2T
Strahlensatz Zentrum M1 :
104
3T : x = 5T : 20
→
x=
3T ⋅ 20
= 12
5T
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Lösungen mit dem CAS
DialogMathe
Algebraische Lösung mit Hilfe von Gleichungen (Gleichungssystem)
Hilfslinie EH
Unbekannte y = CH einführen.
Wir brauchen zwei Gleichungen für die Unbekannten x und y.
Erste Lösungsvariante
1. Strahlensatz Zentrum B:
( 20 − y ) : ( 20 − x ) = 20 : 10
2. Strahlensatz Zentrum E:
( 20 − x ) : y = x : ( 10 − y )
Zweite Lösungsvariante
1. Strahlensatz Zentrum M1 :
x : ( 10 − y ) = 20 : 10
2. Höhensatz im rechtwinkligen Dreieck CEB:
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
y ⋅ ( 20 − y ) = ( 20 − x )
2
105
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
Interpretation der Taschenrechnerlösung
Analysiere die folgende Lösungsvariante.
Einführung von zwei Unbekannten:
y = M1E und z = M1F .
Wir brauchen drei Gleichungen für die
Unbekannten x, y und z.
M1C = 102 + 202 =
500
Strahlensatz Zentrum M1
Pythagoras
1.
x : y = 20 : 500
2.
z : x = 10 : 20
3. y 2 = x 2 + z2
Als Lösung erhalten wir vom Rechner ein Resultat mit einer Konstanten c1.
Diese kann durch eine beliebige Zahl ungleich Null belegt werden.
Das Gleichungssystem hat somit unendlich viele Lösungen, z.B. die Lösung
z = c1 = 1 , y = 2.236 , x = 2
Die Figur zeigt aber, dass es nur eine Lösung geben kann. Wo liegt der Fehler?
Die eingeführten Unbekannten x, y, z sind die Seiten des rechtwinkligen
Dreiecks EFM1, dadurch wird das Problem unterbestimmt.
Lösungsvariante
106
Strahlensatz Zentrum M1 :
x : z = 20 : 10
Strahlensatz Zentrum E:
x : z = ( 20 − x ) : ( 10 − z )
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Ansetzen einer Gleichung
DialogMathe
7.2 Geometrische Denkaufgaben Ansetzen einer Gleichung
7.2.1 Winkelaufgaben
Aufgabe 1
Musterlösung
Schaufigur entwickeln:
Hilfslinien AD und CD .
∆ABD gleichschenklig → ∡DAB = α
∆BCD gleichschenklig, Aussenwinkel bei B = α → ∡BCD =
α
2
1 Unbekannte braucht eine Gleichung:
Innenwinkelsumme ∆ACD : α +
5α
= 180 0 →
2
α
+ α = 1800
2
α = 720
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
107
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
Aufgabe 2
Musterlösung
Schaufigur entwickeln:
∆ABC gleichschenklig → ∡ABC = γ
und
∡CAB = 1800 − 2γ
3 Unbekannte benötigen 3 Gleichungen:
gestreckter Winkel bei F: 2α + β = 1800
Innenwinkelsumme ∆ADE : 1800 − 2γ + β + 900 = 1800
Innenwinkelsumme Viereck DBCF : 2γ + 2β + α = 3600
Gleichungssystem
2α + β = 1800
−β + 2γ = 900
α + 2β + 2γ = 3600
Lösung mit Taschenrechner
108
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Ansetzen einer Gleichung
DialogMathe
Aufgabe 3
Aufgabe 4
Aufgabe 5
Aufgabe 6
Lösungen A3: α = 720
A4: α = 200
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A5: α = 480 / β = 660 / γ = 840
A6: α = 1080
109
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
Aufgabe 7
Aufgabe 8
Aufgabe 9
Aufgabe 10
Lösungen
110
A7: α = 540
A8: α = 360
A9: α = 77 71
0
A10: α = 300
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Ansetzen einer Gleichung
DialogMathe
7.2.2 Flächen und Streckenberechnungen
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Lösungen
A1: A = 6 cm2
A2: x = 3 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A3: x = 21cm
A4: x = 12cm
111
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
Aufgabe 5
Aufgabe 6
Aufgabe 7
Aufgabe 8
Lösungen
112
A5: x = 17 cm
A6: x = 8 cm
A7: x = 5 cm
A8: x = 18 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Geometrische Denkaufgaben Ansetzen einer Gleichung
DialogMathe
7.2.3 Repetitionstest Ansetzen einer Gleichung
Repetitionstest Ansetzen einer Gleichung
Zeit: 25 Minuten
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Lösungen
A1: α = 900
A2: x = 48 cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
A3: x = 18 cm
A4: x = 21cm
113
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
7.3 Trigonometrie am rechtwinkligen Dreieck
7.3.1 Warum Trigonometrie?
Die Trigonometrie (griechisch „Dreiecksmessung“) beschäftigt sich mit der
Berechnung von Seiten und Winkeln in einem Dreieck. Darüber hinaus wird
sie aber auch in nichtgeometrischen Gebieten vielfältig angewendet.
Zusammenhang Streckenlänge und Winkel
Bis jetzt kennen wir in der Geometrie Sätze, die Aussagen über nur Winkel
oder nur Strecken machen.
Beispiele für geometrische Sätze
Dreieckswinkel
Innenwinkelsumme: α + β + γ = 1800 ,
Aussenwinkelsatz: α ' = β + γ
Strecken im rechtwinkligen Dreieck
Pythagoras: a2 + b2 = c 2 ,
Höhensatz: h2 = p ⋅ q
Sind drei Grössen eines Dreiecks bekannt, so kann dieses mit Zirkel und
Lineal konstruiert werden. Ziel der Trigonometrie ist es, ein Dreieck aus
beliebigen drei Stücken zu berechnen, z.B. aus zwei Dreiecksseiten und einem
Winkel können alle anderen Stücke des Dreiecks berechnet werden. Dazu
brauchen wir geometrische Sätze, die Strecken und Winkel enthalten.
Zuordnung zwischen Winkel und Seitenverhältnis
Wir werden sehen, dass es zwischen Winkeln und Strecken keinen direkten
Zusammenhang gibt, dass wir aber im rechtwinkligen Dreieck eine
Zuordnung zwischen Winkeln und Seitenverhältnissen definieren können.
Diese Zuordnungen werden wir Winkelfunktionen (trigonometrische
Funktionen) nennen. Die trigonometrischen Funktionen spielen in der
Technik und dort vor allem zur Beschreibung von periodischen Vorgängen
eine bedeutende Rolle. Ihre Ursprünge reichen sehr weit zurück und im
Gegensatz zu anderen Funktionen liegen ihre Wurzeln deutlich im
geometrischen Bereich. Grundlage aller Berechnungen ist das rechtwinklige
Dreieck. Jedes andere Dreieck können wir durch zeichnen einer Höhe in zwei
rechtwinklige Dreiecke zerlegen.
114
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Trigonometrie am rechtwinkligen Dreieck
DialogMathe
7.3.2 Definition am rechtwinkligen Dreieck
Untersuche den Zusammenhang zwischen den Seitenverhältnissen und den
Winkeln in rechtwinkligen Dreiecken.
Dyn. Arbeitsblatt Seitenverhältnisse rechtwinkliges Dreieck
Dynamisches Arbeitsblatt
GeoGebra: Seitenverhältnisse im rechtwinkligen Dreieck
Zeit: 10 Minuten
Schieberegler:
•
Winkel α für die zwei rechtwinkligen Dreiecke ∆ABC und ∆AB1C1 .
•
Mit dem Faktor k ∈ [ − 10 ; 20 ] kann das Dreieck ∆AB1C1 in der Grösse
verändert werden.
a, b,c sind die Seiten im rechtwinkligen Dreieck ∆ABC
(für den Winkel α sind: a = Gegenkathete, b = Ankathete, c = Hypotenuse)
a1, b1,c1 sind die Seiten im rechtwinkligen Dreieck ∆AB1C1
Arbeitsaufträge
1) Wir betrachten Seitenverhältnisse der drei Seiten a, b und c. Wie viele MögMö
lichkeiten zur Bildung von Verhältnissen gibt es? Notiere dir alle Verhältnisse
und versuche sie zu ordnen.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
115
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
2) Im Arbeitsblatt werden alle Verhältnisse für die zwei verschiedenen Dreiecke berechnet. Verändere den Winkel α und beobachte jeweils die entsprechenden Verhältnisse in den beiden Dreiecken. Was stellst du fest? Kannst du
diese Gesetzmässigkeit mit einem Satz aus der Geometrie begründen? Formuliere einen Satz über die Seitenverhältnisse und den Winkel α am rechtwinkligen Dreieck.
3) Verändere die Grösse des Dreiecks ∆AB1C1 mit Hilfe des Faktors k und
beobachte die Seitenverhältnisse. Was stellst du fest?
Ergebnis
Im rechtwinkligen Dreieck besteht ein Zusammenhang zwischen Winkeln
und Seitenverhältnissen. Ein Winkel im rechtwinkligen Dreieck wird durch
ein Seitenverhältnis eindeutig bestimmt. Und umgekehrt gilt: Wenn ein
Winkel gegeben ist, sind die Seitenverhältnisse eindeutig bestimmt. Es gilt:
Das Verhältnis zweier Seiten am rechtwinkligen Dreieck ist eine Funktion des
Winkels. Diese Zuordnungen ergeben die trigonometrischen Funktionen.
Definition der trigonometrischen Funktionen am rechtwinkligen Dreieck
(3 Winkelfunktionen genügen für die praktische Arbeit):
Definition
sin( α ) =
Gegenkathete
Hypotenuse
cos( α ) =
Ankathete
Hypotenuse
tan( α ) =
Gegenkathete
Ankathete
Zur Information: Die anderen möglichen Verhältnisse definieren den Sekans,
Kosekans und den Kotangens.
sec(α ) =
116
Hypotenuse
Hypotenuse
Ankathete
; csc(α ) =
; cot(α ) =
Ankathete
Gegenkathete
Gegenkathete
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Trigonometrie am rechtwinkligen Dreieck
DialogMathe
Dyn. Arbeitsblatt Definition der trigonometrischen Funktionen
Dynamisches Arbeitsblatt
GeoGebra: Definition_TrigoFunk am rechtwinkligen Dreieck
Zeit: 15 Minuten
Definition der trigonometrischen Funktionen am rechtwinkligen Dreieck
Schieberegler:: Winkel α für das rechtwinklige Dreieck ∆ABC
a, b,c sind die Seiten im rechtwinkligen Dreieck ∆ABC
(für den Winkel α sind: a = Gegenkathete, b = Ankathete, c = Hypotenuse)
Arbeitsaufträge
1) Von den 6 möglichen Seitenverhältnissen genügt es für die Praxis, wenn
wir drei als Winkelfunktionen definieren.
Wie sind die drei Winkelfunktionen sin ( α ) , cos ( α ) und tan ( α ) definiert?
2) Im Allgemeinen
Allgemein sind Berechnungen der Winkelfunktionen
nktionen nur durch den
Rechner
echner möglich (Beachte Einstellung Bogenmass / Gradmass).
Für einige spezielle Winkel gelingt uns die Berechnung von Hand. Berechne
sin ( α ) , cos ( α ) und tan ( α ) für die speziellen Winkel α = 30 0 , 45 0 , 60 0 .
[eventuell α = 150 und 22,50 ]
3) Die beiden Winkel α = 00 und 900 sind im rechtwinkligen Dreieck nicht
definiert. Welche Werte würdest du den drei Winkelfunktionen für diese beibe
den Winkel zuordnen?
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
117
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
Ergebnis
Seitenverhältnisse am rechtwinkligen Dreieck: Das Verhältnis entsprechender Seiten ist konstant. Wenn der Winkel α gegeben ist, sind die Seitenverhältnisse bestimmt. Einem Winkel α können Seitenverhältnisse zugeordnet
werden und umgekehrt kann den Seitenverhältnissen ein Winkel α zugeordnet werden.
Wir sagen: Das Verhältnis zweier Seiten am rechtwinkligen Dreieck ist eine
Funktion des Winkels α (Winkelfunktion = trigonometrische Funktion)
7.3.3 Repetitionstest: Definition trigonometrische Funktionen
Repetitionstest: Definition trigonometrische Funktionen
Zeit: 10 Minuten
Ergänze die fehlenden Winkel bzw. Seitenlängen!
cos
=
f
tan
=
f
sin
=
f
Ergänze sin, cos oder tan
c
(α ) =
d
(β ) =
c
d
(β ) =
e
c
Ergänze sin, cos oder tan und die zugehörigen Winkel
b
a
c
=
b
c
=
a
=
118
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Trigonometrie am rechtwinkligen Dreieck
DialogMathe
Beschrifte die beiden Dreiecke, so dass die dahinter stehenden Beziehungen
gelten.
c
a
b
tan β =
c
sin α =
sin γ =
d
e
tan ϕ =
d
f
Partnerinterview
Sinus Kosinus Tangens rechtwinkliges Dreieck
Zeit: 10 Minuten
Frage 1: Wie lauten die Verhältnisse für die folgenden Winkelfunktionen?
Ermittle aus der nebenstehenden
Figur:
sin(α ) =
cos(ε ) =
tan( ε ) =
cos(β) =
tan(α ) =
sin( γ ) =
Frage 2: Welche Winkel gehören zu den folgenden Verhältnissen?
Ergänze den Winkel (siehe Figur oben):
h
= tan(
u
h
= cos(
m
)
)
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
;
h
= sin(
m
)
;
v
= sin(
n
)
119
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
Diskutiere folgende Aussagen.
• Ein Sinuswert kann nicht über 1 liegen.
• Die Sinuswerte nehmen zu, wenn α von 00 bis 900 zunimmt.
• Ein Tangenswert kann niemals über 1 liegen.
• Ein Kosinuswert kann über 1 liegen.
• Die Kosinuswerte nehmen zu, wenn α von 00 bis 900 zunimmt.
• Der Tangens ist 1, wenn α = 450 ist.
Anwendung
Ein Ballon ist mit einem 300m langen Seil mit
dem Erdboden verbunden. In welcher Höhe
befindet sich der Ballon, wenn windbedingt
das Seil einen Winkel von 700 mit dem
Erdboden bildet?
Merke:
Zentrale Entdeckung der Trigonometrie
Die Beherrschung der Verhältnisse am rechtwinkligen Dreieck sind
fundamental. Durch sie lassen sich die Verhältnisse an beliebigen Dreiecken
ableiten. Mit Hilfe des Einheitskreises können die Definitionen am
rechtwinkligen Dreieck auf beliebige Winkel erweitert werden (siehe später).
120
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Trigonometrie am rechtwinkligen Dreieck
DialogMathe
7.3.4 Spezielle Dreiecke
Mit Hilfe von speziellen Dreiecken lassen sich die trigonometrischen
Funktionen für spezielle Winkel exakt berechnen.
30o – 60o – 90o Dreieck (halbes geleichseitiges Dreieck)
45o – 45o – 90o Dreieck (halbes Quadrat)
Damit lassen sich für die Winkel 30o , 45o und 60o die Seitenverhältnisse
berechnen.
Beispiel: sin ( 300 ) , cos ( 300 ) , tan ( 300 )
1
1
sin ( 300 ) = 2 =
1
2
cos ( 300 ) =
tan ( 30
0
)
3
2
1
=
3
2
1
1 2
2
=
= ⋅
=
3
2 3
2
1
3
=
3
3
Für die Winkel 15o und 22,5o lassen sich die
trigonometrischen Funktionen auch exakt
berechnen. Überlege wie?
Beispiel: sin ( 22,50 ) =
u
1
=
v
2
u+v =1
v=
w=
; w =
u
w
1 + u2
2 ⋅u → u + 2 ⋅u = 1 → u =
1 + u2 =
sin ( 22,50 ) =
1+ 2 − 2 2 + 1 =
u
=
w
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
2 −1
2⋅
2− 2
1
=
2 +1
4−2 2 =
=
2− 2
2⋅
2− 2
2 −1
2⋅
2−
=
2− 2
2
2
121
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
7.3.5 Partnerinterview spezielle Winkel im rechtwinkligen Dreieck
Partnerinterview
Trigo_spezielle Winkel im rechtwinkligen Dreieck
Zeit: 15 Minuten
Frage 1:
Wie kannst du die exakten Werte der Winkelfunktionen für spezielle Winkel ohne
Taschenrechner berechnen?
Berechne für die in unten stehender Tabelle aufgeführten Winkel die Werte mit
Hilfe eines speziellen Dreiecks!
Fülle die Tabelle aus!
α = 300
α = 450
α = 600
sin ( α )
cos ( α )
tan ( α )
Frage 2:
122
Was für Werte ergeben sich für die Winkel α = 00 und α = 900 .
Da diese im rechtwinkligen Dreieck nicht vorkommen, überlege dir die Verhältnisse mit Hilfe von „entarteten Dreiecken“.
sin ( 0 0 ) =
sin(900 ) =
cos ( 00 ) =
cos(900 ) =
tan ( 00 ) =
tan(900 ) =
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Trigonometrie am rechtwinkligen Dreieck
DialogMathe
7.3.6 Übersicht Berechnungen
Gegeben
Gesucht
Zusammenhang
zwei Seiten
dritte Seite
Satz des Pythagoras
zwei Winkel
dritter Winkel
Innenwinkelsumme
Hypotenuse, Winkel
beide Katheten
Kosinus, Sinus
Ankathete, Winkel
Gegenkathete, Hypotenuse
Tangens, Kosinus
Gegenkathete, Winkel
Ankathete, Hypotenuse
Tangens, Sinus
Gradmass / Bogenmass (Taschenrechner Einstellung)
Die folgenden Berechnungen führen wir im Gradmass durch. Du musst deinen Rechner auf das Gradmass (DEG) einstellen! Der Wechsel zum Bogenmass (RAD) wird später wichtig sein.
Beispiel 1:
Gegeben: Hypotenuse c = 9,3 ; Winkel α = 26o
Gesucht: Katheten a und b
sin ( α ) =
→
a = c ⋅ sin ( α ) = 9,3 ⋅ sin ( 26 0
cos ( α ) =
Beispiel 2:
a
c
b
c
→
) = 4,1
b = c ⋅ cos ( α ) = 9,3 ⋅ cos ( 26 0 ) = 8, 4
Gegeben: Hypotenuse c = 9,3 ; Kathete a = 3,1
Gesucht: Winkel α
sin ( α ) =
a
c
Wir kennen das Verhältnis
a 3,1 1
=
= .
c 9,3 3
Den Winkel α erhalten wir mit dem Taschenrechner mit Hilfe der
Umkehrfunktion arc sin ( x ) oder sin−1 ( x )
a
1
α = arc sin   = sin−1   = 19,50
c
3
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
123
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
Beispiel 3:
Für einen Brückenbau muss die Breite
b = FP einer Schlucht ausgemessen
werden. Dazu wird am linken
Schluchtrand eine Strecke AB = 50m
abgesteckt. An den Endpunkten A und
B wird ein Punkt P auf der anderen
Seite der Schlucht anvisiert und die
Winkel α = 420 und β = 670
gemessen. Berechne die Entfernung b = FP ( FP ist rechtwinklig auf AB ).
Einführen einer Unbekannten: x = BF
Dauraus ergibt sich für AF = 50 − x .
Für die beiden Unbekannten b und x
brauchen wir zwei Gleichungen. Diese
erhalten wir aus den zwei rechtwinkligen
Dreiecken ∆FPB und ∆FAP :
∆FAP : tan ( α ) =
b
50 − x
∆FPB : tan ( β ) =
b
x
Auflösen des Gleichungssystems: Beide Gleichungen nach x auflösen und
gleichsetzen b =
124
50 ⋅ tan ( α ) ⋅ tan ( β )
= 32,57m oder mit dem TR:
tan ( α ) + tan ( β )
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Trigonometrie am rechtwinkligen Dreieck
DialogMathe
7.3.7 Übungen Trigonometrie am rechtwinkligen Dreieck
Berechnungen am rechtwinkligen Dreieck
Figur für Aufgabe 1 bis 3
Aufgabe 1
Berechne die fehlenden Seiten.
a) a = 8,9cm , β = 34,80
b) b = 12,0cm , β = 21,80
c) c = 11,04cm , α = 50,10
d) c = 22,3cm , β = 34,30
Aufgabe 2
In einem rechtwinkligen Dreieck ist das folgende Seitenverhältnis bekannt.
Berechne den Winkel α .
a) a : c = 3 : 7
b) b : a = 2 : 3
c) b : c = 17 : 28
d) a : b = 1 : 38
e) a : c = 39 : 31
Aufgabe 3
Berechne die fehlenden Seiten und Winkel.
a) b = 31,4cm , β = 68, 40
b) c = 13,8m , α = 51, 2 0
c) a = 38,7cm , c = 36,3cm
d) c = 25,4dm , β = 85,10
e) a = 54,3cm , b = 18,2cm
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
125
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
Aufgabe 4
Berechne die Länge der Winkelhalbierenden w α eines rechtwinkligen Dreiecks, wenn die Katheten a = 16,6cm und b = 23,2cm messen.
Aufgabe 5
Von einem Dreieck ABC sind die Höhe hc = 6,3cm , die Winkelhalbierende
w γ = 6, 8cm und der Winkel γ = 700 gegeben.
Berechne die Seite c sowie die Winkel α und β .
Aufgabe 6
Ein Rechteck hat die Fläche A = 310cm2 , die Diagonalen schneiden sich unter
einem Winkel β = 1130 . Berechne die Seiten a und b des Rechtecks.
Aufgabe 7
Im quadratischen Einheits – Netz sind die Graden a und b, sowie die Punkte
A und B gegeben.
a) Berechne den Schnittwinkel γ zwischen den Geraden a und b.
b) Berechne die Fläche des Dreiecks ABC, wenn C der Schnittpunkt der Geraden a und b ist.
126
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Trigonometrie am rechtwinkligen Dreieck
DialogMathe
Aufgabe 8
In einem Fluss liegt eine Insel mit einem Turm (siehe Skizze). Am Ufer wird
eine Strecke AB = 50m abgesteckt. Um die Entfernung e = FE des Fusspunktes F des Turmes von der Strecke AB zu bestimmen, werden die beiden Winkel ∡(BAF) = α = 580 und ∡(FBA) = β = 470 gemessen.
Bestimme die Entfernung e?
Aufgabe 9
Wir sollen nach der untenstehenden Skizze den horizontalen Abstand x
zweier Punkte A und B im Gelände bestimmen. Dazu wird im Punkt B eine
Messlatte der Länge a = 2,00 m senkrecht aufgestellt. In A werden die
„Höhenwinkel“ zum unteren und oberen Ende der Messlatte gemessen
α = 15, 8 0 und β = 14,20 .
Aufgabe 10
M ist Kreismittelpunkt.
Radius r = 4
AB = AM
Berechne x = BC
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
127
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
7.3.8 Aufgaben mit Parametern
Aufgabe 1
Einem Quadrat mit der Seite a wird ein zweites
einbeschrieben. Bestimme die Seitenlänge b des
a
einbeschriebenen Quadrates aus a und α .
b
α
Aufgabe 2
Berechne die Strecke x, wenn
b, α und β gegeben sind.
Aufgabe 3
Zeige, ausgehend von den Definitionen der trigonometrischen Funktionen
am rechtwinkligen Dreieck,
dass:
a) tan(α ) =
b)
128
sin(α )
cos(α )
sin(α )
= 1
cos(β)
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Flächeninhalt eines Dreiecks mit Trigo
DialogMathe
7.3.9 Lösungen Übungen Trigonometrie am rechtwinkligen Dreieck
Aufgabe 1
a) b = 6,2cm , c = 10,8cm
c) a = 8,47cm , b = 7,08cm
b) a = 30,0cm , c = 32,3cm
d) a = 18,4cm , b = 12,6cm
Aufgabe 2
a) α = 25, 4 0 b) α = 56,3 0 c) α = 52, 6 0 d) α = 1, 510 e) keine Lösung
Aufgabe 3
a) a = 12,4cm , c = 33,8cm , α = 21, 6 0
b) a = 10,8m , b = 8,65m , β = 38,80
c) keine Lösung
d) a = 2,17dm , b = 25,3dm , α = 4, 9 0
e) c = 57,3cm , α = 71, 5 0 , β = 18,50
Aufgabe 4
w α = 24, 4cm
Aufgabe 5
c = 11,2cm , α = 77,10 , β = 32,90
Aufgabe 6
a = 21,6cm , b = 14,3cm
Aufgabe 7
a) γ = 63, 40 b) A = 6,4
Aufgabe 8
e = 32,1m
Aufgabe 9
x = 66,8m
Aufgabe 10
x = 5,37
Aufgaben mit Parametern
Aufgabe 1
b=
a
sin ( α ) + cos ( α )
Aufgabe 2
x=
b
tan ( α + β ) − tan ( α )
Aufgabe 3
sin ( α ) a c a
= ⋅ = = tan ( α )
cos ( α ) c b b
a) sin ( α ) =
a
b
; cos ( α ) =
c
c
b) cos ( β ) =
sin ( α ) a c
a
;
= ⋅ =1
c
cos ( β ) c a
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
;
129
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
7.4 Flächeninhalt eines Dreiecks mit Trigo
Gegeben:
zwei Dreiecksseiten p, q und der
Zwischenwinkel ϕ
Fläche des Dreiecks:
A = 1 ⋅ p ⋅ q ⋅ sin ( ϕ )
2
Ein beliebiges Dreieck kann durch die Höhe in zwei rechtwinklige Dreiecke
zerlegt werden.
sin ( ϕ ) =
hc
p
→ hc = p ⋅ sin ( ϕ )
A = 1 ⋅ q ⋅ hc = 1 ⋅ q ⋅ p ⋅ sin ( ϕ )
2
2
Aufgabe
Berechne den Flächeninhalt A des gleichschenkligen Dreiecks aus dem Umkreisradius R und dem Basiswinkel α = 630
130
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Pythagoras für beliebige Dreiecke
DialogMathe
7.5 Pythagoras für beliebige Dreiecke
7.5.1 Pythagoras für rechtwinklige Dreiecke
γ = 90o
c 2 = a2 + b2
7.5.2 Pythagoras für spitzwinklige Dreiecke
γ < 90o
Kosinussatz
c 2 = a2 + b2 − 2ab ⋅ cos ( γ )
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
131
Algebraische Behandlung von Geometrieaufgaben
DialogMathe
7.5.3 Dynamisches Arbeitsblatt Kosinussatz als Flächensatz
Dynamisches Arbeitsblatt
GeoGebra Datei: Kosinussatz als Flächensatz
Zeit: 15 Minuten
Die Ecke C des Dreiecks ABC kann mit der Maus bewegt werden.
Achtung: Die dynamische Konstruktion ist nicht definiert, wenn sich die Ecke
C innerhalb des Halbkreises befindet (stumpfwinklige Dreiecke).
Arbeitsaufträge:
1) Verschiebe die Ecke C auf den Halbkreis
Halb
(Thaleskreis,
kreis, rechtwinkliges
Dreieck). Überzeuge dich, dass der folgende Flächensatz gilt:
c 2 = a2 + b2 (Pythagoras)
2) Spezialfall: Ziehe C weg vom Halbkreis, so dass γ kleiner als 90o wird.
Verändere die Position von C so, dass der Winkel bei A
α = ∡ ( CAB ) = 90o wird.
3) Zeige, das für eine beliebige Position der Ecke C ausserhalb des HalbHal
2
2
2
kreises gilt: c = a + b − 2ab ⋅ cos ( γ ) . Benutze dazu rechtwinklige
Teildreiecke.
132
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Kreisumfang
DialogMathe
8 Kreisberechnungen
Definition Kreis
Der Kreis ist die Ortslinie aller Punkte, die von einem Punkt den gleichen Abstand haben.
Am Kreis werden die folgenden Bezeichnungen verwendet.
Bezeichnungen
Kreislinie k
Mittelpunkt M
Durchmesser d
Radius r
Sehne s
Sekante g
Tangente t
Passante p
Merke
• Der Radius r steht im Berührungspunkt B senkrecht auf der Tangente t.
• Das Lot (Rechtwinklige MF ) vom Mittelpunkt M auf eine Sehne s halbiert
die Sehne. Der Fusspunkt F ist Mittelpunkt der Sehne CD , d.h. CF = FD .
8.1 Kreisumfang
Ein Kreis mit Radius r hat den Umfang: U = 2 π ⋅ r , wobei π = 3,14159…… ist.
Herleitung als Grenzwert: Einem Kreis mit Durchmesser d lassen sich reguläre n – Ecke einbeschreiben und umschreiben. Der Umfang U des Kreises liegt
dann zwischen dem Umfang un des einbeschriebenen und dem Umfang Un
des umschriebenen n – Ecks. Mit zunehmender Eckenzahl kommen sich un
und Un beliebig nahe. Für den Kreisumfang U gilt dann un < U < Un .
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
133
Kreisberechnungen
DialogMathe
8.1.1 Das Bogenmass
Mit dem Kreisumfang lässt sich ein neues Winkelmass definieren:
Definition Bogenmass
Unter dem Bogenmass eines Winkels verstehen wir die Masszahl der Länge
des zugehörigen Bogens auf dem Einheitskreis.
Die in der Dreieckslehre übliche Methode, Winkel in Graden zu messen, ist
für unsere Zwecke ungeeignet. Ein geeignetes Mass, Winkel durch Zahlen
und nicht durch Grade, zu messen, ist das Bogenmass. Die Grundidee liegt
dabei in der Beobachtung, dass jeder Winkel, im Mittelpunkt eines
vorgelegten Kreises angetragen, einen Ausschnitt des Kreisesbogens liefert.
Da allerdings ein Winkel bei verschieden grossen Kreisen unterschiedliche
grosse Bögen ausschneidet, ist eine Festlegung auf einen bestimmten Kreis
zwingend.
Einheitskreis
Zur Winkelmessung durch Bögen
werden wir daher stets einen Kreis mit
Radius 1 und Mittelpunkt im Ursprung
des Koordinatensystems zugrunde
legen, den sog. Einheitskreis.
Jedem gemäss nebenstehender Skizze
eingetragenem Winkel α kommt nun
neben seinem (orientierten) Gradmass α
auch sein (orientiertes) Bogenmass
⌢
α = b , d.h. die Länge des von ihm ausgeschnittenen Bogens, zu. Dabei bezieht
sich der Zusatz "orientiert" auf die Vereinbarung, dass im Gegenuhrzeigersinn
eingezeichnete Winkel positive Masszahlen haben, und Winkeln, die im
Uhrzeigersinn eingetragen sind, negative Masszahlen zukommen. Der Winkel
im Bogenmass ist eine Zahl und hat somit keine Einheit (Masszahl der
Bogenlänge). Um den Winkel im Bogenmass trotzdem mit einer Einheit
nennen zu können, wird das rad (Radiant) verwendet.
134
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Kreisfläche
DialogMathe
8.1.2 Bogenlänge
= b = r ⋅α
AB
(Winkel im Bogenmass)
8.2 Kreisfläche
Ein Kreis mit Radius r hat die Fläche: A = r 2 ⋅ π , wobei π = 3,14159…… ist.
8.2.1 Kreissektor
A Kreissektor =
A Kreissektor =
b ⋅ r α ⋅ r2
=
2
2
b ⋅r
.
2
Vergleiche die Flächenberechnung mit derjenigen des Dreiecks A =
g⋅h
.
2
Die Bogenlänge b entspricht der Grundlinie g und der Radius der Höhe h.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
135
Kreisberechnungen
DialogMathe
8.2.2 Kreissegment
A Kreissegment = A Kreissektor − A Dreieck
Berechne A Kreissegment für α =
136
π
.
3
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Kreisfläche
DialogMathe
8.2.3 Partnerinterview Bogenmass, Bogenlänge, Kreissektor
Partnerinterview Kreis
Bogenmass, Bogenlänge, Kreissektor
Zeit: 10 Minuten
Frage 1: Wie ist das Bogenmass definiert? Erkläre anhand einer Figur!
Frage 2: Wie lassen sich Winkel im Gradmass ins Bogenmass umrechnen?
Entwickle eine Umrechnungsformel. Benutze dazu die Definition des Bogenmasses und den Dreisatz. Teste deine Formel für einige spezielle Winkel!
Frage 3: Wie lautet die Formel zur Berechnung einer Bogenlänge und eines Kreissektors
für einen gegebenen Winkel α und einen Kreis mit Radius r?
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
137
Kreisberechnungen
DialogMathe
8.2.4 Übungen schraffierte Kreisflächen
Berechne die schraffierten Flächen
138
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
DialogMathe
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Kreisfläche
139
Kreisberechnungen
8.2.5
DialogMathe
Übungen Kreis
Übung 1
Sektoren, Bogenlängen
a) Der wievielte Teil der Sektorfläche ASB ist
schraffiert?
b) Berechne das Verhältnis der Bogenlängen b : B , wenn α gegeben
, b = Bogen PQ
ist. B = Bogen RS
Übung 2
Gegeben ist die Höhe h = CD des Dreiecks ABC mit den Winkeln
α = ∡CAB = 45o und β = ∡ABC = 60o .
Der gezeichnete Kreis hat sein Zentrum in C und den Radius h.
Berechne:
a) den Umfang U des Dreiecks ABC.
b) die Fläche A des Dreiecks ABC.
c) die Länge des Bogens EF.
d) die schraffierte Fläche.
Übung 3
Berechne den Umfang UABC und den Flächeninhalt A der schraffierten Fläche,
wenn r gegeben ist.
140
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Kreisfläche
DialogMathe
Übung 4
Einem Kreisring mit gegebenem Aussenradius R
und dem Innenradius r wird ein gleichschenkliges
Dreieck ABC einbeschrieben. Die Schenkel AC
und BC sind doppelt so lang wie die Basis AB. Wie
gross muss r sein, damit die Flächen des Dreiecks
ABC und des Kreisrings gleich gross sind?
Übung 5
Berechne die Fläche des Kreissegments AB.
Gegeben: ∡(ASB) = 170 , AB = 34
Übung 6
In der Figur ist R = 2r. Berechne ausgedrückt durch r
a) die Länge von a
b) die schraffierte Fläche
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
141
DialogMathe
8.2.6 Lösungen Kreisberechnungen
Übungen schraffierte Kreisflächen
π
a) A Schraffiert = s2 ⋅  1 − 
4

π
c) A Schraffiert =
⋅ d2
16
b) A Schraffiert = s2
π
d) A Schraffiert = s2 ⋅  − 1 
2

 2π
3
e) A Schraffiert = r 2 ⋅ 
−
2 
 3
 3
π 
g) A Schraffiert = s2 ⋅ 
−

4
48


f) A Schraffiert = s2 ⋅  1 −

3 +
π 
3 
 3
π 
h) A Schraffiert = s2 ⋅ 
−

12
24


Übungen Kreis
A Schraffiert
3
=
A Sektor
4
Übung 1
a)
Übung 2
a) U = ( 1 +
2+
b) b : B = 1 : 1
3 ) ⋅ h = 4,146 ⋅ h
3+ 3 2
⋅ h = 0,789 ⋅ h2
6
= 5 π ⋅ h = 1,309 ⋅ h
c) b = EF
12
1
π
d) A =  −  ⋅ h2 = 0,1073 ⋅ h2
8
2
b) A =
142
r2
2+ 2
;
A
=
⋅
r
≈
3,27r
2
4 
Übung 3

UABC =  2 −

Übung 4
r = 0,881 ⋅ R
Übung 5
A Segment = A Sektor − A Dreieck = 1962,34 − 1933,75 = 28,59
Übung 6
a) a = 4 ⋅ 2 ⋅ r ≈ 5,657 r
2 + π⋅
b) A = 1,651 ⋅ r 2
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Oberflächen und Volumen einiger Körper
DialogMathe
9 Stereometrie
9.1 Oberflächen und Volumen einiger Körper
Körper
Prisma
Quader
Beschreibung und Figur
Prisma mit der Grundfläche G und der
Höhe h. Beispiel: Gerades fünfseitiges
Prisma (Kanten rechtwinklig zu G)
Quader mit den Kantenlängen a, b und c.
Prisma mit Rechteck als Grundfläche
Oberfläche
Volumen
O = 2G + M
V = G ⋅h
O=
V = a⋅b ⋅c
O = 6a2
V = a3
O = 2G + M
V = π ⋅ r2 ⋅ h
2 (a ⋅ b + b ⋅ c + a ⋅ c )
Würfel
Hexaeder
Quader mit gleichen Kantenlängen a
Zylinder
Zylinder mit dem Grundkreisradius r und
der Höhe h
= 2 π ⋅ r 2 + 2π ⋅ r ⋅ h
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
143
Stereometrie
DialogMathe
Pyramide Pyramide mit der Grundfläche G und der
Höhe h
O =G+M
V = 31 G ⋅ h
Beispiel: Quadratische Pyramide mit der
Grundseitenlänge a, der Höhe h und der
Dreieckshöhe hS der Seitenfläche.
O = a2 + 4 ⋅
Tetraeder
Reguläres Tetraeder (4 gleichseitige Dreiecke): Kantenlänge s
h=
Kegel
2
3
a ⋅ hS
2
V = 31 a 2 ⋅ h
O = 3 ⋅ s2
V = 122 ⋅ s3
O =G+M
V = 31 π ⋅ r 2 ⋅ h
⋅ s ; hS = 2s 3
Kegel mit dem Radius r, der Höhe h und
der Mantellinie m
= π ⋅ r2 + π ⋅ r ⋅ m
144
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Oberflächen und Volumen einiger Körper
DialogMathe
Oberfläche Kegel
G = π ⋅ r2
b = 2π ⋅ r
m⋅b
M=
= π ⋅r ⋅m
2
Kugel
Kugel mit Radius r
In der vorhergehenden ZuZ
O = 4π ⋅ r 2
Gerades Prisma
V = 34 π ⋅ r 3
Schiefes Prisma
sammenstellung sind die
Formeln für sogenannte
gerade Körper angegeben.
Diese gelten aber auch für
schiefe Körper, wie der Satz
von Cavalieri verdeutlicht.
Dass die Formel V = G ⋅ h auch
für schiefe Prismen gilt, zeigt
das Prinzip von Cavalieri. Ein
gerades Prisma werde durch
Schnitte parallel zur Grundfläche in Scheiben zerlegt. Bei seitlicher VerschieVerschi
bung bleibt das Volumen unverändert. Werden die einzelnen Scheiben immer
dünner, so stellt der Körper rechts im Grenzfall ein schiefes Prisma dar.
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
145
Stereometrie
DialogMathe
Satz von Cavalieri
Alle Körper, die in jeweils gleicher HöH
he die gleichen Querschnittsflächen
besitzen, haben das gleiche Volumen.
Volumen
Anwendung Kugelvolumen
Um die Formel für das Volumen der Kugel
gel herzuleiten, wird die Halbkugel
nach dem Satz von Cavalieri mit einem Körper verglichen, dessen Volumen
bekannt
kannt ist. Der Vergleichskörper
Vergleichskörper ist ein Zylinder, aus dem ein Kegel herausherau
genommen
nommen wurde. Der Zylinder hat den gleichen Radius wie die Halbkugel
und die Höhe ist ebenfalls r. Gelingt es zu beweisen, dass die QuerschnittsQuer
flächeninhalte
inhalte beider Körper in beliebiger
be
Höhee gleich sind, dann sind auch
ihre Volumeninhalte
meninhalte gleich.
Restkörper
körper = Zylinder – Kegel
Halbkugel
Schnittfläche = Kreisring
Schnittfläche = Kreis
Kreisring auf der Höhe x hat äusseren
Satz von Pythagoras:
Radius r und innneren Radius x (gleich(gleic
rx2 = r 2 − x 2
schenkliges Dreieck):
(
A Ring = π ⋅ r 2 − π ⋅ x 2 = π ⋅ r 2 − x 2
A Ring = A Kreis
Also: VKugel =
146
⇒
4
3
)
(
A Kreis = π ⋅ rx2 = π ⋅ r 2 − x 2
VHalbkugel = VZylinder − VKegel = π ⋅ r 2 ⋅ r − 31 ⋅ π ⋅ r 2 ⋅ r =
2
3
)
⋅ π ⋅ r3
⋅ π ⋅ r3
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Berechnungen mit Schnittebenen
DialogMathe
9.2 Berechnungen mit Schnittebenen
Um im dreidimensionalen Raum Berechnungen durchzuführen, verwenden
wir Schnittebenen. Diese sind so zu wählen, dass die zu berechnenden Winkel
oder Längen in wahrer Grösse erscheinen.
Beispiel 1: Volumen eines regulären Tetraeders
Das reguläre Tetraeder ist eine dreiseitige
dreiseitige Pyramide, deren Kanten alle die
gleiche Länge haben.
Räumliche Skizze des Tetraeders
Schnittebene UVW für Berechnung
Volumenberechnung
(
h2 = s2 − 32 h1
)
2
h2 = s2 − s3 = 2s
3
2
mit h1 = 2s 3
2
→
2
V = 31 G ⋅ h = 31 ⋅ s 4⋅ 3 ⋅
h=
2
3
2
3
⋅s
,
2
G = s 4⋅ 3
⋅ s = 122 ⋅ s3
Oberflächenberechnung
O = 4G = 4 ⋅ s 4⋅ 3 = 3 ⋅ s2
2
Zusatzaufgaben:
Das reguläre Tetraeder besitzt eine In – und eine Umkugel.
Berechne die Radien aus der Kantenlänge s.
Berechne den Winkel α zwischen Grundfläche und Seitenfläche.
s 6 ; r
s
Lösungen: rInkugel = 12
Umkugel = 4 6 ; cos ( α ) =
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
1
3
→
α = 70,53o
147
Stereometrie
DialogMathe
9.3 Ähnliche Körper
Eine quadratische Pyramide wird auf halber Höhe geschnitten. Die so entstandene kleine Pyramide ist ähnlich zur grossen Pyramide. Es gilt:
Streckenverhältnis (Höhen):
hgross
=2
hklein
Flächenverhältnis (Grundfläche):
Volumenverhältnis:
Ggross
= 22 = 4
Gklein
Vgross
= 23 = 8
Vklein
Das Volumen der kleinen angeschnittenen Pyramide beträgt: Vklein = 81 Vgross .
Das Volumen des Restkörpers (Pyramidenstumpf):
VPyramidenstumpf = Vgross − Vklein = 78 Vgross
Beispiel
Ein randvoll gefülltes kegelförmiges Glas beinhaltet
0,27 Liter Flüssigkeit. Wie viele Liter wurden dem Glas
entnommen, wenn der Flüssigkeitsspiegel um
h
gesunken ist?
3
V = VKegel − V1 ; VKegel = 0,27 Liter ;
h1 = 32 ⋅ h
3  2 ⋅ h 3
3
h1 
2
8

=   =  3  =   =
 h 
VKegel  h 
27
3


8
8
→ V1 =
⋅ VKegel =
⋅ 0,27 = 0,08 Liter
27
27
V1
148
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Stereometrieaufgaben
DialogMathe
9.4 Stereometrieaufgaben
Beispiel 1: Abgeschnittene Würfelkante
Eine Ecke eines Würfels wird abgeschnitten (siehe Figur). Es entsteht ein
Tetraeder mit den Kantenlängen a, a
und b. Berechne:
a) Das Volumen des Tetraeders (Es
gibt eine einfache Lösung)
b) Die Höhe des Tetraeders in Bezug
auf das Dreieck PQR als Grundfläche.
c) Das Volumen des Tetraeders mit Hilfe der Höhe hA und des Dreiecks
PQR als Grundfläche.
Zahlenbeispiel: a = 3 cm, b = 5cm
Beispiel 2: Pyramide mit einbeschriebenen Quader
Die Kanten einer Pyramide mit quadratischer Grundfläche haben alle die
Länge s. Auf der Grundfläche der Pyramide steht ein Quader mit quadratischer Grundfläche. Die Diagonale der Grundfläche des Quaders hat ebenfalls
die Länge s. Die Kanten der Deckfläche des Quaders liegen in den Seitenflächen der Pyramide.
Berechne das Verhältnis der Volumina VQuader : VPyramide .
Beispiel 3: Halbkugel mit einbeschriebenem Würfel
Einer Halbkugel mit dem Radius r wird ein Würfel einbeschrieben.
Berechne das Verhältnis der Volumina VWürfel : VHalbkugel .
Beispiel 5: Auftrieb eines Kreiskegels
Ein gerader Kreiskegel Mit dem Radius R, der Höhe H und der Dichte ρ
schwimmt im Wasser mit der Spitze nach unten ohne umzukippen.
Bestimme die Höhe der Wasserlinie am Kegel.
Zahlenbeispiel: R = 4 cm, H = 5 cm, ρ = 0,8kg / dm3 , ρ W = 1kg / dm3
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
149
Stereometrie
DialogMathe
Beispiel 6: Zwei Pyramiden in einem Würfel
In welchem Verhältnis steht das Volumen des
Würfels mit der Kantenlänge a zum Volumen
des stark ausgezogenen Körpers?
Der Lösungsweg muss ersichtlich sein!
Beispiel 7: Pyramide im Kegel
In einem mit der Spitze nach unten in die Erde
gesteckten geraden Kreiskegel mit dem Radius r
und der Höhe h = 3r wird eine gerade quadratische
Pyramide mit der Grundkantenlänge r und der
Höhe hP = 32 r gestellt. Wie viel Prozent des PyraPyr
midenvolumens sind innerhalb des Kegels?
Beispiel 8: Tetraeder im Würfel,
Wü
Oktaeder im Tetraeder
In einem Würfel mit der Kantenlänge a
kann durch sechs Flächendiagonalen
Flächendi
ein
Tetraeder festgelegt
festgel
werden. Verbindet
man die Kantenmitten
Kantenmi
des Tetraeders, so
entsteht ein Oktaeder.
Berechne das Verhältnis der drei Volumen.
150
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
Rotationskörper, Guldinsche Regel
DialogMathe
9.5 Rotationskörper, Guldinsche Regel
Lässt man eine ebene Fläche oder eine Linie
um eine Achse rotieren, so entsteht
en
ein Körper
bzw. eine Fläche
Volumenregel
Das Volumen eines Rotationskörpers ist gleich dem Produkt aus dem Inhalt
der auf einer Seite der Drehachse liegenden (erzeugenden) Fläche und der
Länge des Weges, den der Flächenschwerpunkt bei einer Volldrehung um die
Drehachse zurücklegt.
Weg des Flächenschwerpunkts:
Flächenschwerpunkts 2π ⋅ rA
Erzeugende Fläche: A (Dreiecksfläche)
Volumen des Rotationskörpers:
V = 2π ⋅ rA ⋅ A
Beispiel
Das schraffierte gleichseitige Dreieck wird 3600
360 um die
eingezeichnete Achse gedreht (Eine Ecke des Dreiecks
liegt auf der Achse und eine Seite ist parallel zur Achse).
Berechne das Volumen des so entstandenen RotationsRotation
körpers.
Guldin: V = A△⋅2πrS
3
3
A△= 21 ⋅ s ⋅ h = 21 ⋅ s ⋅ 2 ⋅ s = 4 ⋅ s2
rS = 32 ⋅ h = 32 ⋅ 23 ⋅ s = 33 ⋅ s
V = A△⋅2π ⋅ rS = 4 ⋅ s2 ⋅ 2π ⋅ 3 ⋅ s = 2π ⋅ s3
3
3
alternativ: V = VZylinder − 2VKegel
( 2 ⋅ s ) ⋅ π ⋅ s = 34π ⋅ s
= 31 ⋅ h π 21 s = 31 ⋅ ( 2 ⋅ s ) π ⋅ 21 s = 8π ⋅ s
VZylinder = h2 π ⋅ s =
VKegel
3
2
2
3
3
2
3
V = VZylinder − 2VKegel = 34π ⋅ s3 − 4π ⋅ s3 = 2π ⋅ s3
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF
151
Stereometrie
DialogMathe
Beispiel 1:: Volumen eines Torus (Autoreifen)
Berechne das Volumen des skizzierten
skiz
ten Torus mit R = 10 cm und r = 3 cm.
Beispiel 2: Schwerpunkt eines Halbkreises
Berechne die Lage des Schwerpunkts
Schwer
s einer Halbkreisfläche mit dem Radius r.
Mantelflächenregel
Der Inhalt der Mantelfläche eines Rotationskörpers ist gleich dem Produkt aus
der Länge des auf einer Seite der Drehachse liegenden (erzeugenden) KurvenKurve
stücks und der Länge des Weges, den der Schwerpunkt des erzeugenden
Kurvenstücks bei einer Volldrehung um die Drehachse zurücklegt.
Weg des Linienschwerpunkts:
Linien
2π ⋅ r L
Erzeugende Linie: L (Strecke)
Mantelfläche des Rotationskörpers:
M = 2π ⋅ rL ⋅ L
152
Lerneinheit 2 | Geometrisches Denken | 2013/14 | ©BF