Report als PDF - IWR - Universität Heidelberg
Werbung

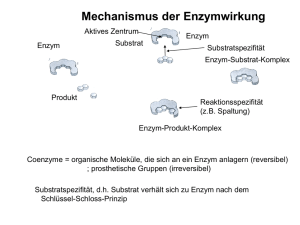
Von: Andrea Marschall Marion Braun David Owald Martin Schulz Mathematik-Projektarbeit im Rahmen des Studiengangs Molekulare Biotechnologie 2.Semester, SS2003 Ruprecht-Karls Universität Heidelberg INHALTSVERZEICHNIS 1. Einführung....................................................................................................... 1 2. Abkürzungsregister......................................................................................... 1 3. Modellierung................................................................................................... 2 3.1 Einleitung.............................................................................................. 2 3.2 Das Massenwirkungsgesetz................................................................... 2 3.3 Der Steady state ................................................................................... 3 3.4 Der Quasi steady state........................................................................... 4 3.5 Die Michaelis-Menten Gleichung ........................................................ 4 3.6 Der Einfluss der Michaelis-Menten Konstante..................................... 5 3.7 Der Einfluss der maximalen Umsetzungsgeschwindigkeit................... 7 3.8 Die Wechselzahl.................................................................................... 7 3.9 Inhibitoren............................................................................................. 8 4. Ausblick........................................................................................................ 11 4.1 MWC und Kooperative Kinetik.......................................................... 11 4.1.1 Das MWC-Modell............................................................................... 11 4.1.2 Allosterisch regulierte Enzyme........................................................... 12 4.2 Induced fit............................................................................................ 12 5. Anhang...............................................…........................................................ 13 1. Einführung Enzyme sind biochemische Katalysatoren und sind daher von entscheidender Bedeutung für Stoffwechselvorgänge. Sie ermöglichen und beschleunigen Stoffumwandlungen bei vergleichsweise niedrigen Temperaturen, wie der Körpertemperatur eines lebenden Organismus. Enzyme bestehen meist aus einem Protein, das eine Bindungsstelle für den umzusetzenden Stoff, das Substrat, besitzt. Enzym und Substrat passen hierbei wie Schlüssel und Schloss zueinander, Enzyme sind also substratspezifisch. Durch Bindung von Substrat an ein Enzym entsteht der Enzym-Substrat-Komplex (siehe hierzu Abbildung 1). Die Bindung des Substrats an das Enzym bewirkt dabei eine Abb.1 (aus [8]): Enzym-Substrat-Reaktion Absenkung der Aktivierungsenergie, so dass die Umsetzung in kurzer Zeit bei Körpertemperatur ablaufen kann. Nach Ablauf der Reaktion löst sich das Reaktionsprodukt vom Enzym. An die frei gewordene Bindungsstelle kann sich nun erneut Substrat anlagern. Enzyme regulieren den Stoffwechsel, können jedoch auch selbst reguliert werden. Zusätzlich zur Bindungsstelle für das Substrat können noch Bindungsstellen für Regulatoren vorliegen. Auf diese Weise können Enzyme durch andere Moleküle gehemmt oder aktiviert werden. Zum Verständnis der Rolle der Enzyme und der Reaktionsmechanismen im Organismus ist besonders die Enzymkinetik von Nutzen. Sie beschäftigt sich hauptsächlich mit Reaktionsraten und dem zeitlichen Verhalten der Reaktanden. Durch den Vergleich von experimentell ermittelten Graphen mit verschiedenen Theorien kann auf Reaktionsmechanismen geschlossen werden. Im Rahmen dieser Arbeit werden zwei Modelle der Enzymkinetik, der Steady state und der Quasi steady state, vorgestellt. Man benutzt in der Enzymkinetik solche Modelle, weil die ablaufenden biochemischen Prozesse sehr komplex sind und es ungünstig wäre, exakte mathematische Beschreibungen zur Untersuchung der Vorgänge zu verwenden. Hierbei ist es also sinnvoller, Näherungen zu machen, wobei nebensächliche Effekte vernachlässigt und wesentliche Aspekte im Modell erfasst werden. Zudem wird durch Approximation die Handhabbarkeit der beiden Modelle erheblich verbessert, so können die Differentialgleichungen relativ einfach gelöst werden. Ihre Ergebnisse leiten über in die MichaelisMenten Kinetik, die dann an zahlreichen Abbildungen erläutert wird. Aus ihr kann man nun Vorhersagen über experimentelle Prozesse machen, wenn die Anfangsbedingungen bekannt sind. Allerdings konnte man hier dann in manchen Fällen Abweichungen feststellen, die beispielsweise durch Inhibitoren, welche Enzyme hemmen, zustande kommen. Weitere Erklärungen werden im Ausblick genannt. 2. Abkürzungsregister Im Rahmen dieser Arbeit werden folgende Abkürzungen verwendet: S für Substrat [,-konzentration] P für Produkt [,-konzentration] E für freies Enzym [,-konzentration] ET für die Gesamtkonzentration an Enzym (gebunden und frei) C für Enzymsubstratkomplex [,-konzentration] KM für Michaelis-Menten Konstante 1 k1,k-1,k2 für geschwindigkeitsbestimmende Faktoren I für Inhibitor [,-konzentration] X für Enzyminhibitorkomplex [,-konzentration] KI für Dissoziationskonstante des Inhibitors 3. Modellierung 3.1 Einleitung Als Einstieg in die mathematischen Modelle der Enzymkinetik soll das Michaelis-MentenDiagramm (Abbildung 2) zur Veranschaulichung und zum besseren Verständnis dienen. Es beschreibt die Wechselwirkung zwischen Substrat- und Enzymkonzentration mit der Zeit. Abb. 2 (aus[9]): Michaelis-Menten Diagramm: Zur Zeit t=0 ist noch kein Enzymsubstratkomplex[ES] vorhanden, alles Enzym [E] liegt frei vor. Sobald Substrat [S] hinzugefügt wird, wird der Komplex gebildet und dann auch Produkt [P] umgesetzt. Diese Kurven lassen sich nun mit Funktionen beschreiben. Hierfür werden zuerst die Anfangsbedingungen festgelegt: (1) E(0) = E0 ; S(0) = S0 ; C(0) = C0 ; P(0) = P0 Meist geht man aber wie in Abbildung 2 davon aus, dass zur Zeit t = 0 noch kein Komplex vorliegt und deshalb gilt: E(0) = E0 ; S(0) = S0 ; C(0) = 0 ; P(0) = 0 3.2 Das Massenwirkungsgesetz Angenommen Substrat S reagiert nun mit Enzym E zu Enzymsubstratkomplex C, welcher aber zum Teil auch wieder in seine Edukte S und E zerfallen kann, dann kann man ihre jeweiligen Konzentrationen (Zahl der Moleküle pro Volumeneinheit) als Funktionen S(t), E(t) und C(t) darstellen. Dabei geht man davon aus, dass die Bildungsrate von C proportional ist zur Abnahme der Konzentrationen von S und E. Also führt eine Verdoppelung oder Verdreifachung der Konzentration von S dazu, dass auch die Bildungsrate von C verdoppelt 2 oder verdreifacht wird. Das liegt daran, dass durch die Zunahme der Konzentration die Zeit kürzer wird, in der sich die Moleküle S und E erst “finden“ müssen. Somit ist die Geschwindigkeit, mit der C gebildet wird, festgelegt durch die Konzentrationen von E und S und einem zu diesen Molekülen spezifischen geschwindigkeitsbestimmendem Faktor k: v = k*E*S Nun ist bekannt, dass die Geschwindigkeit eine nach der Zeit abgeleitete Funktion beschreibt. In diesem Fall wird die Konzentration nach der Zeit differenziert und es resultiert die Umsetzungsgeschwindigkeit v mit [v]=µg/mol. Für die Reaktion k2 k -1 E + S ' C E + P gilt deshalb: k1 (2) dE/dt = -k1 E*S + (k -1 + k2) C In Worten bedeutet dies, dass sich die Änderung der Konzentration an freiem Enzym E ergibt aus der Rückreaktion (Zerfall) des Enzymsubstratkomplexes, der Weiterreaktion des Komplexes zu freiem Enzym E und Produkt P abzüglich der Bildung des Enzymsubstratkomplexes, bei der ja der Reaktion freies Enzym entzogen wird, jeweils multipliziert mit den korrespondierenden Geschwindigkeitsfaktoren (oberhalb der jeweiligen Reaktionspfeile). Analog ergibt sich für die anderen Konzentrationsänderungen: (3) dS/dt = -k1 E*S + k -1C (4) dC/dt = k1 E*S – (k -1 + k2) C (5) dP/dt = k2 C wobei v(P)=dP/dt der geschwindigkeitsbestimmende Schritt ist, weil diese Reaktion am längsten dauert, oder anders ausgedrückt, weil v(P) am kleinsten ist. Addiert man nun Gleichung (2) und (4) stellt man fest: (6) dE/dt + dC/dt = 0 ⇔ d(E + C) / dt = 0; also E(t) + C (t) = konst. Die Gesamtkonzentration an gebundenem und freiem Enzym ist demnach zu jedem Zeitpunkt gleich der Gesamtkonzentration ET: (7) E(t) + C(t) = E0 + C0 = ET ⇔ E(t) = E0 + C0 – C(t) Der Steady state und der Quasi steady state sind nun zwei Annahmen der Enzymkinetik, mit deren Approximationsgrundlage die Differentialgleichungen solcher dynamischer Systeme einfacher zu lösen sind. Sie werden nachfolgend erläutert. 3.3 Der Steady state Beim Steady state nimmt man an, dass die Anfangskonzentration an Substrat so groß ist, dass die Abnahme durch die Umsetzung vernachlässigbar klein ist. Deshalb gilt hier S(t) = S0 zu jedem beliebigen Zeitpunkt, solange noch viel mehr Substrat vorhanden ist, als Enzyme besetzt werden können, also solange S>>E. Ersetzt man E in Gleichung (4) durch E(t) aus Gleichung (7) und berücksichtigt, dass hier S = S0 gilt, folgt: dC/dt = k1( E0 + C0 – C)S0 – (k -1 + k2)C (8) ⇔ dC/dt = k1( E0 + C0)S0 – (k1S0 + k -1 + k2)C 3 Die Lösung dieser Differentialgleichung liefert die Funktion (9) C(t) = (C0 + C°) exp [(-k1S0 + k –1 + k2) t ] + C° mit (10) C°≡(E0 – C0)S0/(KM + S0) (11) KM≡(k -1 + k2)/k1 Wobei KM Michaelis-Menten Konstante genannt wird ([KM]=mol). Sie setzt sich nur aus den geschwindigkeitsbestimmenden Faktoren zusammen und ist spezifisch für jedes EnzymSubstrat-Paar. C° ist ebenfalls eine Konstante; sie fungiert in der Funktion als Asymptote, an die sich die Komplexkonzentration mit der Zeit nähert. 3.4 Der Quasi steady state Auch im Quasi steady state wird zur Lösung der dynamischen Systeme eine Vereinfachung vorgenommen, welche aber die tatsächlich stattfindenden Prozesse genauer beschreibt. Solange die Substratkonzentration noch wesentlich höher ist als die Enzymkonzentration, dass folglich alle Enzyme gesättigt vorliegen können, betrachtet man die Substratkonzentration als eine Funktion S(t). Die Vereinfachung beim Quasi staedy state liegt also nur noch in der Annahme, dass sich die Komplexkonzentration der Asymptote C° annähert und dann nicht mehr steigt. Man setzt dann in Gleichung (8) dC/dt = 0 0 = k1 (E0 + C0)S0 – (k1S0 + k -1 + k2)C ⇔ C = k1 (E0 + C0)S0 / (k1S0 + k -1 + k2) = (E0 + C0)S0 / [(k1S0 + k -1 + k2) / k1] ⇔ C = (E0 + C0)S0 / [((k -1 + k2) / k1)+ S0] (11) C = (E0 + C0)S0 / (KM + S0) Unter Berücksichtigung dass S0 ≠S erhält man die Quasi steady state Gleichung, die eine gute Näherung liefert, solange sich S “langsam genug“ ändert: (12) C(t) = (E0 + C0)S(t) / (KM + S(t)) “Langsam genug“ bedeutet hier, dass sich die Änderung der Konzentration von S über einen im Vergleich zur Änderung von C viel größeren Zeitraum erstreckt. 3.5 Die Michaelis-Menten Gleichung Mit dem Ergebnis aus (12) ist es nun möglich, die Differentialgleichung (5) wie folgt auszudrücken: (13) dP/dt = k2 (E0 + C0)S / (KM + S) Michaelis und Abb.3 (aus[10]) Menten Wie bereits bekannt ist, definiert die Ableitung einer Konzentration nach der Zeit die Umsetzungsgeschwindigkeit und da diese vom Komplex zum Produkt am kleinsten ist, wird dP/dt oder auch dS/dtdie Geschwindigkeit der Reaktion genannt. Mit der Voraussetzung, dass zu Beginn noch kein Substratkomplex vorliegt, also C0=0, und ausgehend von der Tatsache, dass die Reaktionsgeschwindigkeit gemessen wird, ehe S beträchtlich von der Ausgangskonzentration S0 abweicht, kann man, ausgehend von (13), folgende Gleichung aufstellen: (14) v = k2E0S0 / (KM + S0) 4 Die Reaktionsgeschwindigkeit wächst also mit der Substratkonzentration und wird maximal, wenn S hinsichtlich KM sehr groß wird, also wenn gilt: (15) vmax = lim v = lim k2E0S0 / (KM + S0) = k2E0 S0→∞ S0→∞ Unter Berücksichtigung dieses Ergebnisses in Gleichung (14), ergibt sich die MichaelisMenten Gleichung: (16) v = vmax S0 / (KM + S0) Hier hilft jetzt die Michaelis-Menten Konstante, um genauere Aussagen über die Umsetzungsgeschwindigkeit v zu treffen: Ist ihr Wert gleich der der Anfangskonzentration an Substrat S0, also KM = S0, dann bedeutet das, dass die Reaktionsgeschwindigkeit die Hälfte ihres Maximalwertes erreicht, oder anders ausgedrückt, dass die Hälfte der aktiven Zentren besetzt sind. (17) v = vmax S0 / (S0 + S0) = ½ vmax für KM = S0 Diese Werte vmax und KM lassen sich in einer graphischen Auftragung der Geschwindigkeit gegen die Substratkonzentration leicht ablesen (Michaelis-Menten Diagramm), indem man durch Annäherung der Funktion gegen die Maximalgeschwindigkeit vmax diesen Funktionswert halbiert ( ½ vmax) und den korrespondierenden Wert auf der Abszisse abliest. Dieser entspricht der Michaelis-Menten Konstante KM: Abb. 4 (aus[11]): Zusammenhang von vmax und KM: Bei KM erreicht die Reaktionsgeschwindigkeit die Hälfte ihres Maximalwertes 3.6 Der Einfluss der Michaelis-Menten Konstante Werte der Michaelis-Menten Konstante bewegen sich in einem Bereich von 10-7 mol bis 10-1 mol. Ändert sich nun KM, hat dies Auswirkungen auf die Enzymumsetzung und somit auf die graphische Darstellung. Die maximale Umsetzungsgeschwindigkeit vmax bleibt gleich, aber sie wird bei einer Halbierung schon bei niedrigeren Substratkonzentrationen erreicht, als bei einer Verdoppelung (siehe Abbildung 5). Da KM die gleiche Einheit wie die Substratkonzentration hat, bedeutet eine kleine KM, dass ½ vmax schon bei einer geringen 5 Substratkonzentration erreicht wird. Im Gegensatz dazu stellt sich ½ vmax und damit schließlich vmax bei einer großen KM erst spät ein (vgl. Gleichung (17)). Wenn die Enzymkonzentration im Verhältnis zur Substratkonzentration sehr hoch ist und somit keinen Einfluss mehr auf die Umsetzungsgeschwindigkeit nimmt (da vmax nahezu erreicht ist), hängt sie nur noch von der Affinität des Substrats zum Enzym ab. Man sieht also, dass ein kleines KM das Substrat (gerade bei geringen Mengen) schneller umsetzt, das heißt das Enzym eine höhere Effizienz besitzt als ein Enzym mit großem KM. Diese Tatsache lässt sich am besten an einem „greifbaren“ Beispiel verständlich machen. Beim Konsum von Alkohol wird dieser durch die Alkoholdehydrogenase in einer NAD+ (Reduktionsäquivalent) abhängigen Reaktion zu Acetaldehyd abgebaut: Alkohol (CH3CHOH) + NAD+ Alkoholdehydrogenase Acetaldehyd (CH3CHO) + NADH + H+ Dieses führt im Körper zu den bekannten physiologischen Reaktionen (einem „Kater“). Die Fähigkeit viel Alkohol zu „vertragen“ hängt also davon ab, wie schnell der Organismus das Acetaldehyd unschädlich machen, d.h. abbauen kann: Acetaldehyddehydrogenase Acetaldehyd (CH3CHO) + NAD+ Acetat (CH3COO-) + NADH + H+ Hierfür bedient sich die Zelle zweier Isoenzyme, welche beide als Acetaldehyddehydrogenase bezeichnet werden. Zwar können sie dasselbe Substrat umsetzen, weisen aber eine unterschiedliche Struktur auf. Das Effizientere dieser beiden Enzyme mit einer kleinen KM (10-6 mol) ist in den „Kraftwerken der Zelle“, den Mitochondrien, lokalisiert. Das zweite, weniger effiziente Enzym (KM = 10-2 mol) befindet sich in der Zellflüssigkeit, dem Cytosol. Einige Menschen, besonders Südostasiaten und Indianer besitzen eine große Prävalenz für die Bildung einer funktionsuntüchtigen Version des mitochondrialen Enzyms. Die Folge ist, dass nur das ineffizientere, cytosolische Enzym den Abbau des Acetaldehyds katalysiert. Dadurch wird es wesentlich langsamer abgebaut und diffundiert durch einen Konzentrationsgradienten in den Blutstrom. v/ [µmol/s] vmax = 50 µmol/s Abb.5 (aus[12]): Die maximale Umsetzungsgeschwindigkeit vmax wird bei kleiner KM schneller erreicht. KM = 0,250 mmol ½KM = 0,125 mmol 2KM = 0,500 mmol [S] / [mmol] v / [µmol/s] Abb.6: In Scilab wird Gleichung (16) mit den Werten KM=0,25mmol und vmax=50µmol/s geplottet. Besonders für große Substratkonzentrationen S0 (wie vorausgesetzt) ist die Übereinstimmung mit der experimentell ermittelten Kurve der Umsetzungsgeschwindigkeit aus Abb.4 sehr gut. [S]/[mmol] 6 3.7 Der Einfluss der maximalen Umsetzungsgeschwindigkeit Verändert sich die maximale Umsetzungsgeschwindigkeit vmax und bleibt dabei KM konstant, stellt sich ½ vmax bei genau derselben Substratkonzentration ein, weil diese ja von KM abhängt (siehe Abbildung 7). Da vmax linear eingeht läuft die Substratumsetzung bei einer Verdoppelung von vmax doppelt so schnell ab. Eine besonders große Auswirkung hat eine Veränderung von vmax wieder bei geringen Substratkonzentrationen im Vergleich zur vorhandenen Menge an Enzym (wie sie im Körper bestehen). Hier steigt die Umsetzungsgeschwindigkeit bei großem vmax exponentiell an. Somit ist die Umsetzung um ein Vielfaches schneller als bei kleinem vmax. v/ [µmol/s] vmax = 50 µmol/s vmax*2 = 100 µmol/s vmax /2 = 25 µmol/s KM = 0,25 mmol [S] / [mmol] Abb.7 (aus[12]): Eine Änderung der Maximalgeschwindigkeit hat keine Auswirkung auf die MichaelisMenten Konstante 3.8 Die Wechselzahl Die effektive Umsetzungsgeschwindigkeit lässt sich auch quantitativ ausdrücken. Wie eingangs erwähnt hängt die Maximalgeschwindikeit der Reaktion von der Umsetzung des Enzymsubstratkomplexes zu Produkt und freiem Enzym ab. Im günstigsten Fall sind alle Enzyme gesättigt, also alle aktiven Zentren vollständig besetzt, und es gilt nach Gleichung (7) dann ET = C. Daraus folgt für Gleichung (5): (18) vmax = k2 * ET Durch Umformung erhält man die Wechselzahl k2 (in der Literatur auch kcat genannt): (19) k2 = vmax /ET Sie beschreibt die Anzahl der umgesetzten Substratmoleküle pro Sekunde durch ein Enzymmolekül (vergleichbar mit der Frequenz in der Physik). Eine andere Art der Beschreibung ist die Zeit, die pro Umsetzung eines Substratmoleküls vergeht. Enzym Carboanhydrase Acetylcholinesterase Penicillinase Chymotrypsin DNA-Polymerase 1 Lysozym Wechselzahl / s 600.000 25000 2000 100 15 0,5 Zeit / 1Umsatz 1,7 µs 40 µs 500 µs 10 ms 67 ms 2s 7 Die Carboanhydrase, ein zinkhaltiger Komplex, katalysiert die Hydratisierung von Kohlendioxid (CO2) im Blut zu Hydrogencarbonat (HCO3-). Dieser Prozess ist für den Abtransport des bei der Zellatmung entstandenen CO2 und zur Abgabe in der Lunge gleichermaßen wichtig, wie für das Konstanthalten des ph-Werts im Blut (7,2 bis 7,4). Zur Reizweiterleitung zwischen Neuronen wird Acetylcholin in den synaptischen Spalt entlassen und besetzt auf der postsynaptischen Seite (dem Empfängerneuron) die Acetylcholinrezeptoren. Um eine Dauerreizung zu verhindern und die Rezeptoren für den nächsten Nervenimpuls frei zu machen, wird Acetylcholin durch die Acetylcholinesterase zu Acetat und Cholin gespalten, welches wieder ins präsynaptische Neuron aufgenommen und für den nächsten Impuls zu Acetylcholin regeneriert wird. Sowohl die Carboanhydrase, als auch die Acetylcholinesterase besitzen essentielle Aufgaben im Körper, die sehr schnell ausgeführt werden müssen. Im Laufe der biochemischen Evolution haben diese Enzyme katalytische Perfektion erreicht, d. h. sie setzen vorhandenes Substrat, sobald es erst das aktive Zentrum erreicht hat, so schnell um, dass ihre Geschwindigkeit prinzipiell nur noch von der Substratfindung, also dem zufälligen Zusammentreffen von Enzym und Substrat in Lösung abhängt. Penicillase ist ein Abwehrstoff, den Bakterien zur Spaltung und damit Unschädlichmachung von Penicillinen benutzen. Chymotrypsin spielt zusammen mit Trypsin bei der Proteinspaltung im Dünndarm eine entscheidende Rolle. DNA-Polymerase 1 dient bei der Zellteilung zur Replikation (Vervielfältigung) der DNA. Ein Bespiel für ein sehr langsames Enzym stellt das Lysozym dar. Es befindet sich in Speichel und Tränenflüssigkeit und spaltet den Mureinsakkulus (die Zellwand) von Bakterien. Es wirkt somit antibakteriell. Sichtbar wird die langsame Katalyse durch die Tatsache, dass Karies-Bakterien im Mund den Zucker metabolisieren und damit Säure ausscheiden, die den Zahnschmelz zerstört. Würde das Lysozym schneller die Zellwand dieser Bakterien zerstören und durch den Überdruck damit die Bakterien lysieren, hätten viele Menschen wahrscheinlich weniger Probleme mit Karies. 3.9 Inhibitoren Inhibitoren sind Stoffe, die im Allgemeinen Enzyme hemmen, also in ihrer Funktion die Umsetzungsgeschwindigkeit negativ beeinflussen. Man unterscheidet zwei Arten: kompetitive und nicht-kompetitive Hemmung. Die Mathematik stellt uns nun Mittel zur Verfügung, um eine Aussage über das Vorhandensein und die Art von Inhibitoren zu treffen. Durch eine doppeltreziproke Auftragung der Geschwindigkeit gegen die Substratkonzentration im nach dem Namen seiner „Erfinder“ benannten Lineweaver-Burk Diagramm lässt sich sowohl die Michaelis-Menten Konstante KM und die maximale Umsetzungsgeschwindigkeit vmax, als auch gegebenenfalls die Art der Hemmung bestimmen. Die doppeltreziproke Michaelis-Menten Gleichung lautet: (20) 1/v = (1/vmax) *(1 + KM/S0) Durch Umformung lässt sich die Linearität besser darstellen: (21) 1/v = (KM/vmax) * 1/S0 + 1/vmax wobei nun (KM/vmax) die Steigung beschreibt und (1/vmax) der Ordinatenabschnitt der Funktion ist. 8 Im Diagramm entspricht der Schnittpunkt des Graphen mit der Abszisse dem negativen Kehrwert der Michaelis-Menten Konstante KM und der Schnittpunkt mit der Ordinate dem Kehrwert der maximalen Umsetzungsgeschwindigkeit vmax. Wie bereits aus dem Michaelis-Menten Diagramm hervorging, verändert sich KM bei einer Verdoppelung bzw. Halbierung von vmax nicht und umgekehrt. In der linearisierten Gleichung ändert sich also nur die Steigung: 1/v in [s/µmol] KM = 0,250 mmol 2KM = 0,500 mmol ½ KM = 0,125 mmol vmax = 50 µmol/s Abb.8 (aus[12]): Verdoppelung bzw. Halbierung von KM ändert vmax nicht 1 / [S] in [mmol] 1/v in [s/µmol] KM = 0,25 mmol vmax = 50 µmol/s vmax*2 = 100 µmol/s vmax/2 = 25 µmol/s Abb.9 (aus[12]): Verdoppelung bzw. Halbierung von vmax ändert den Wert von KM nicht 1 / [S] in [mmol] Zurück zu den Inhibitoren: Kompetitive Inhibitoren konkurrieren mit dem Substrat um das aktive Zentrum. Sie binden also an die Bindungsstelle des Substrats am Enzym, wodurch diese besetzt ist und kein Substratmolekül mehr akzeptieren kann. Man unterscheidet hierbei immer zwischen reversibler und irreversibler Hemmung. Während Drogen wie zum Beispiel Kokain und Heroin im Allgemeinen einen zeitbegrenzten Rauschzustand herstellen, nämlich genau solange, wie sie bis zu ihrem Abbau die Bindungsstellen besetzen, tritt bei einer Cyanidvergiftung (Cyankali z.B.) eine irreversible Bindung des Cyanats an das Hämoglobin auf, wodurch die Erythrozyten (roten Blutkörperchen) keinen Sauerstoff mehr aufnehmen können und der Organismus schließlich erstickt. Im Weiteren wird von reversibler Hemmung ausgegangen. 9 Eigentlich müsste durch diese Besetzung der aktiven Zentren mit Inhibitoren eine Geschwindigkeitsverminderung auftreten. Da sich aber durch Zugabe von zusätzlichem Substrat die maximale Umsetzungsgeschwindigkeit vmax wiederherstellen lässt, fließt sie nicht in unsere Berechnung mit ein. Das lässt sich dadurch erklären, dass durch einen enormen Überschuss an Substrat natürlich der Inhibitor verdrängt wird (vorausgesetzt die Affinität für den Inhibitor ist gleich der Affinität für das Substrat). Dadurch ist die Menge an EnzymInhibitor Komplex X und damit blockiertem Enzym gering gegenüber dem Enzym-Substrat Komplex C. Da allerdings durch die Bildung des Enzym-Inhibitor Komplexes der Reaktion vorübergehend Enzym für die Umsetzung von Substrat zu Produkt entzogen wird, scheint sich die Effizienz der Umsetzung zu verändern. Es wird durch Unwissen weiterhin davon ausgegangen, dass das gesamte Enzym ET nur Enzym-Substrat Komplexe bildet, aber man stellt fest, dass weniger C als normal vorliegt. Dadurch scheint sich die Michaelis-Menten Konstante KM verändert zu haben. Sie scheint größer geworden zu sein, da ja die Effizienz gesunken ist. Diese angebliche Änderung von KM wird als KMapp (vom engl. apparent) bezeichnet. Mathematisch lässt sich die kompetitive Hemmung durch das Aufstellen einer Dissoziationskonstanten KI für den Inhibitor beschreiben: (22) KI = E*I /X KMapp lässt sich dann folgendermaßen bestimmen: (23) KMapp = KM * (1 + I/KI) Im Lineweaver-Burk Diagramm (Abbildung 10) äußert sich dies in einer (angeblichen) Vergrößerung vom KM und damit in einer Vergrößerung des negativen Kehrwerts. (Achtung: die Bezeichnungen größer und kleiner sind hier irreführend, da im Lineweaver-Burk Diagramm ja der negative Kehrwert von KM aufgetragen wird). Damit wird die Steigung größer. Wenn man nun die tatsächliche MichaelisMenten Konstante dieser Umsetzung kennt und im Diagramm feststellt, dass sich die Steigung in diesem Versuch erhöht hat, während sich gleichzeitig der Schnittpunkt mit der Abszisse verschoben hat, kann man mit Sicherheit sagen, dass ein kompetitiver Inhibitor vorliegt. Abb.10 (aus[13]): Kompetitive und nicht kompetitive Hemmung und deren Auswirkungen auf vmax und KM Nicht-kompetitive Hemmung liegt immer dann vor, wenn ein Inhibitor (oder allgemeiner: Stoff) nicht das aktive Zentrum besetzt, sondern das Enzym auf andere Weise behindert. Am bekanntesten ist hier die allosterische Hemmung, bei der der Inhibitor eine eigene Bindungsstelle am Enzym besitzt. Bindet der Inhibitor nun an diese Stelle, führt das Enzym eine Konformationsänderung durch und versiegelt somit das aktive Zentrum für das Substrat. Effektiv werden alle betroffenen Enzymmoleküle der Umsetzung entzogen und die Gesamtenzymkonzentration ET scheint sich zu vermindern. Alle nicht betroffenen Enzyme setzen weiterhin mit derselben Affinität und Effizienz Substrat um, nur dass eben ihre Anzahl gesunken ist. Dadurch erniedrigt sich die erreichbare maximale Umsetzungsgeschwindigkeit vmax, was sich im Lineweaver-Burk Diagramm in einer Erhöhung der Steigung bei einer gleichzeitigen Verschiebung des Ordinatenabschnitts äußert (siehe Abbildung 10). Ist diese 10 Tatsache im Vergleich zum erwarteten Graphen feststellbar, so kann mit Sicherheit davon ausgegangen werden, dass eine nicht-kompetitive Hemmung vorliegt. 4. Ausblick 4.1 MWC und Kooperative Kinetik Die Vorhersagen des Lineweaver-Burk Diagramms über die reziproke Reaktionsgeschwindigkeit wurden in zahlreichen experimentellen Beobachtungen bestätigt. Dennoch konnten in anderen Fällen Abweichungen festgestellt werden, welche sich durch die nachfolgenden Theorien erklären lassen: 1. Allosterische Theorie von Monod, Wyman, Changeux, welche auch MWC Theorie genannt wird, aus dem Jahre 1965 2. „Induced-fit Theorie von Koshland, Nemethy, Filmer aus dem Jahre 1966 4.1.1 Das MWC-Modell Bei dem MWC-Modell wird angenommen, dass ein Enzym aus vielen gleichen Untereinheiten besteht und diese in zwei verschiedenen Formen existieren können. Das Enzym muss also als Oligomer betrachtet werden, wobei das Enzym einmal als inaktive (nicht reaktive) T-Form und zum anderen als aktive (reaktive) R-Form vorliegen kann. Der Übergang findet statt, sobald Substrat zum gebunden werden vorhanden ist. Im Folgenden soll ein Protein mit nur zwei Bindungsstellen als einfachster Fall betrachtet werden. Hierfür geht man davon aus, dass das Protein nur von der aktiven Phase in die inaktive übergehen kann, solange kein Ligand gebunden ist: T0 R0 b ' f R1 k- ' 2k+s R2 2k- s ' s s k+s Abb.11 (nach[1]): Beschreibung des Proteins, wobei f die Reaktionsrate vom inaktiven T0-Zustand zum aktiven R0-Zustand und b umgekehrt darstellt, analog gilt dies auch für die Reaktionsraten k. s symbolisiert gebundenes Substrat bzw. Liganden. Das Substrat bindet an eine Untereinheit mit der Rate k+ und dissoziiert mit der Rate k-. Bei der Hinreaktion von R0 zu R1 wird der statistische Faktor 2 eingefügt, welcher durch die Möglichkeit des Liganden, an zwei Stellen gebunden werden zu können, zustande kommt. Aus diesem Grund und wegen der Tatsache, dass die Übergänge zwischen T- und R-Formen im selben Enzym konzertiert vorliegen, also in einem Enzym gleichzeitig verlaufen, ändert sich die Umsetzungsgeschwindigkeit der Reaktion. Sie weicht also von den Vorhersagen des Lineweaver-Burk Diagramms ab. 11 Eine genauere mathematische Ausarbeitung des Modells ist im Rahmen dieser Arbeit nicht möglich. 4.1.2 Allosterisch regulierte Enzyme Wie bereits in 3.9 angesprochen lassen sich allosterische Enzyme durch andere Moleküle regulieren. Sie besitzen Bindungsstellen außerhalb der katalytischen Untereinheit, welche vom aktiven Zentrum abgetrennt sind. So verschiebt ein Inhibitor, gebunden an das Enzym, das Gleichgewicht in Richtung inaktiver T-Form. Folglich wird die Nettoreaktivität des Enzyms konzertiert herabgesetzt und damit die Produktbildungsgeschwindigkeit erniedrigt. Allosterische Enzyme können also nicht konsequent der Michaelis-Menten Kinetik folgen. Vielmehr zeigt die Kurve der Produktbildung als Funktion der Substratkonzentration einen sigmoiden Verlauf, wie er in Abbildung 12 zu sehen ist. Das lässt sich nun dadurch erklären, dass die Untereinheiten konzertiert von der Tin die R-Form und umgekehrt reagieren. Dieses wird Kooperativität genannt. Die sigmoide Kurve stellt also eine Überlagerung zweier Michaelis-Menten Kurven dar, von denen eine der T-Form und eine der R-Form entspricht, wobei eine Substratzunahme die R-Form begünstigt. Inhibitoren bzw. Regulatoren wirken sich nun auf das R-T-Gleichgewicht aus. Somit bewirkt ein Inhibitor beispielsweise, dass die durch Substratbindung entstehenden kooperativen Effekte herabgesetzt werden (aus[14]): Allosterisch regulierte Enzyme weisen und zum Erreichen einer bestimmten Abb.12 einen sigmoiden Verlauf der Reaktionsgeschwindigkeit Reaktionsgeschwindigkeit dann mehr bei steigender Substratkonzentration auf Substrat benötigt wird. Bildlich kann man sich daher vorstellen, dass die erste Phase der sigmoiden Kurve eine flachere Steigung besitzt. Ein allosterischer Aktivator hingegen stabilisiert die R-Form, wodurch die Reaktivität erhöht wird und die Kurve eine größere Steigung annimmt. 4.2 Induced fit Das „Induced fit“ Modell geht im Gegensatz zum konzertierten Modell nicht davon aus, dass ein Enzym entweder in der R-Form oder in der T-Form vorliegt, sondern dass die Strukturveränderung des aktiven Zentrums sequentieller Natur ist. Hierbei beeinflusst die Bindung eines Substrats an eine Bindungsstelle nur die benachbarten Zentren, nicht aber alle Zentren des Enzyms. Es muss somit nicht zu einem Übergang eines ganzen Enzyms von der einen in die andere Form kommen; die Zentren wechseln den Umständen entsprechend von der R-Form in die T-Form und umgekehrt. Im sequentiellen Modell kann also auch negative Kooperativität stattfinden. 12 Abb.13 (aus[15]): Binden eines Substrats an eine Untereinheit und resultierende Konformationsänderung der Bindungsstelle. 5. Anhang Literaturverzeichnis 1. Segel, Lee A., Modeling dynamic phenomena in molecular and cellular biology, chapter 4 2. Yeargers, Edgar K. et al, An Introduction to the Mathematics of Biology 3. Murray, J. D., Mathematical Biology 4. Berg, Jeremy M.; Stryer, Lubert; Tymoczko, John L.; Biochemie 5. Bisswanger, Hans, Enzymkinetik, 3.dt.Auflage ISBN 3-527-30343-3 6. Ahlers, J.; Arnold, A., Enzymkinetik, 2.Auflage ISBN 3-437-20253-7 7. Fromm, H.J.,Inicial Rate Enzyme Kinetics ISBN 3-540-07375-2 8. http://omega.dawsoncollege.qc.ca/ray/metabol/metabol.htm 9. http://wine1.sb.fsu.edu/kinetics/kinetics.htm 10. http://cwx.prenhall.com/horton/medialib/media_portfolio/text_images/FG05_0301C.JPG 11. http://www.fst.rdg.ac.uk/courses/fs916/lect9/lect9.htm 12. www.stark.kent.edu/~cearley/PChem/Kinetics/Kinetics.htm 13. http://users.rcn.com/jkimball.ma.ultranet/BiologyPages/E/EnzymeKinetics.html 14. http://www.ehu.es/biomoleculas/ENZ/ENZ3.htm 15. http://www.emc.maricopa.edu/faculty/farabee/BIOBK/BioBookEnzym.html 13