Karl-Heinz Pfeffer Analysis für technische Oberschulen
Werbung

Karl-Heinz Pfeffer
Analysis für technische Oberschulen
Karl-Heinz Pfeffer
Analysis für
technische Oberschulen
Ein Lehr- und Arbeitsbuch
8., überarbeitete und erweiterte Auflage
Mit 311 Abbildungen und über 1650 Aufgaben
STUDIUM
Bibliografische Information der Deutschen Nationalbibliothek
Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der
Deutschen Nationalbibliografie; detaillierte bibliografische Daten sind im Internet über
<http://dnb.d-nb.de> abrufbar.
Bis zur 6. Auflage erschien das Buch unter dem Titel Analysis für Fachoberschulen
beim gleichen Verlag.
1. Auflage 1981
Nachdruck 1983
2., durchgesehene Auflage 1985
Nachdruck 1986
3., verbesserte Auflage 1988
3 Nachdrucke
4., verbesserte und erweiterte Auflage 1998
5., durchgesehene Auflage 2000
6., überarbeitete Auflage 2003
Nachdruck 2004
7., überarbeitete und erweiterte Auflage 2007
Nachdruck 2009
8., überarbeitete und erweiterte Auflage 2010
Alle Rechte vorbehalten
© Vieweg+Teubner Verlag | Springer Fachmedien Wiesbaden GmbH 2010
Lektorat: Thomas Zipsner | Imke Zander
Vieweg+Teubner Verlag ist eine Marke von Springer Fachmedien.
Springer Fachmedien ist Teil der Fachverlagsgruppe Springer Science+Business Media.
www.viewegteubner.de
Das Werk einschließlich aller seiner Teile ist urheberrechtlich geschützt. Jede
Verwertung außerhalb der engen Grenzen des Urheberrechtsgesetzes ist ohne
Zustimmung des Verlags unzulässig und strafbar. Das gilt insbesondere für
Vervielfältigungen, Übersetzungen, Mikroverfilmungen und die Einspeicherung
und Verarbeitung in elektronischen Systemen.
Die Wiedergabe von Gebrauchsnamen, Handelsnamen, Warenbezeichnungen usw. in diesem Werk
berechtigt auch ohne besondere Kennzeichnung nicht zu der Annahme, dass solche Namen im
Sinne der Warenzeichen- und Markenschutz-Gesetzgebung als frei zu betrachten wären und daher
von jedermann benutzt werden dürften.
Umschlaggestaltung: KünkelLopka Medienentwicklung, Heidelberg
Technische Redaktion: Stefan Kreickenbaum, Wiesbaden
Bilder: Graphik & Text Studio, Dr. Wolfgang Zettlmeier, Barbing
Druck und buchbinderische Verarbeitung: MercedesDruck, Berlin
Gedruckt auf säurefreiem und chlorfrei gebleichtem Papier.
ISBN 978-3-8348-1024-3
V
Vorwort
Analysis für technische Oberschulen ist das Nachfolgewerk der seit 1981 aufgelegten „Analysis für
Fachoberschulen“, ergänzt durch Elemente der analytischen Geometrie und Grundlagen zum Rechnen
mit komplexen Zahlen. Es ist ein Lehr- und Arbeitsbuch für Lernende an Fach- und Berufsoberschulen
sowie an Fachgymnasien und für Studierende an Fachhochschulen im Erstsemester, ausgerichtet auf die
Fachrichtung Technik.
Die spezifisch technische Akzentuierung der Inhalte ist dabei so behutsam erfolgt, dass innermathematische Problemstellungen nicht zu kurz kommen und eine Verwendung des Buches in beruflichen Oberschulen nichttechnischer Fachrichtungen ebenfalls gut möglich ist.
Es berücksichtigt in besonderem Maße unterschiedliche mathematische Vorkenntnisse, indem wiederholende Thematik angeboten wird, die je nach Bedarf mehr oder weniger selbstständig von den Nutzern
erarbeitet werden kann.
Der didaktische Leitgedanke dieses Buches beinhaltet, grundlegende Kenntnisse über Funktionen zu
vermitteln, ohne dabei die Theorie überzubewerten. Dazu gehört es, hinführend zu den klassischen Methoden der Analysis auch die hierfür wesentlichen elementaren Rechentechniken und geometrischen
Denkweisen bereitzustellen und einzuüben.
Das geschieht zunächst durch bewusst breit angelegte Überlegungen zu den linearen und quadratischen
Funktionen, an die sich die einschlägigen Nullstellenermittlungen ganzrationaler Funktionen höheren
Grades anschließen. Abgerundet wird die elementare Funktionenlehre durch Betrachtung der trigonometrischen Grundfunktionen und mündet ein in die Erarbeitung der allgemeinen Sinusfunktion.
Dieser Einstieg in die Analysis, je nach Lerngruppe und Lernintention abkürzbar, hat den Vorteil, dass
nach der sich anschließenden optionalen Erarbeitung des Grenzwertbegriffes über Folgen bzw. über
Funktionen den Lernenden die Problemstellungen der Differential- und der Integralrechnung durchsichtiger erscheinen: Grundsätzliche Vorgehensweisen werden wieder aufgegriffen (Wiederholungseffekt!)
und gemäß Spiralprinzips in erweitertem Zusammenhang angewandt.
Besonders erwähnenswert ist, dass die Integralrechnung nicht über Ober- und Untersummenermittlung,
sondern anschaulich-direkt über Flächeninhaltsfunktionen eingeführt wird.
Neu ist der Einbezug von Elementen der Analytischen Geometrie und grundlegender Ausführungen zum
Rechnen mit komplexen Zahlen; auf „Nahtstellen“ zur Analysis wird bewusst hingewiesen.
Viele Beispielaufgaben mit Lösungen (Ź) erleichtern das selbstständige Einüben des Stoffes. Das umfangreiche, zum großen Teil ganzheitlich-anwendungsbezogene Aufgabenmaterial ermöglicht handlungsorientierte Unterrichtsansätze, schülerorientierte Übungsphasen und intensive Vorbereitung auf
Lernkontrollen. Die Aufgabenanordnung ist innerhalb derselben Thematik weitmöglichst im Sinne einer
methodischen Reihe schwierigkeitsgraddifferenziert erfolgt; besonders schwierige Aufgaben sind kursiv
gekennzeichnet.
Die mit * versehenen Inhalte dienen der Abrundung. Sie können ohne Einfluss auf das weitere Vorgehen
auch weggelassen werden. - Im Unterricht bieten sie sich durchaus als Themen für Referate an.
Meinen Kolleginnen und Kollegen danke ich für die über die Jahre hinweg erfolgten hilfreichen Anregungen und Bestätigungen, meiner Ehefrau Gertrud Annedore für unermüdliches Korrekturlesen.
Besonderer Dank gilt Herrn Thomas Zipsner aus dem Lektorat des Vieweg+Teubner Verlages für konstruktive Hinweise und kritische Sichtung des Manuskriptes.
Hannover, im Februar 2010
Karl-Heinz Pfeffer
VII
Inhaltsverzeichnis
Mathematische Zeichen und Begriffe ..............................................................................
X
Teil A: Analysis .................................................................................................................
1
1 Die reellen Zahlen ........................................................................................................
2
1.1
Die Grundeigenschaften der reellen Zahlen .........................................................
1.1.1 Von den natürlichen zu den reellen Zahlen .............................................
1.1.2 Lagebeziehungen reeller Zahlen .............................................................
Das Rechnen in R .................................................................................................
1.2.1 Der binomische Satz ................................................................................
1.2.2 Gleichungen und Ungleichungen ............................................................
2
2
11
15
15
19
2 Funktionenlehre ...........................................................................................................
39
1.2
2.1
2.2
2.3
2.4
2.5
Grundlagen ...........................................................................................................
2.1.1 Paarmengen .............................................................................................
2.1.2 Funktionen ..............................................................................................
Ausgewählte elementare Funktionen ....................................................................
2.2.1 Lineare Funktionen .................................................................................
2.2.2 Quadratische Funktionen ........................................................................
*2.2.3 Lineare und quadratische Betragsfunktionen ..........................................
Ganzrationale Funktionen .....................................................................................
2.3.1 Reine Potenzfunktionen ..........................................................................
2.3.2 Ganzrationale Funktionen als verknüpfte Potenzfunktionen ..................
2.3.3 Nullstellen ganzrationaler Funktionen ....................................................
2.3.4 Kurvenverlauf und Symmetrie ................................................................
Wurzelfunktionen .................................................................................................
2.4.1 Umkehrfunktionen (Umkehrrelationen) ..................................................
2.4.2 Wurzelfunktionen im engeren Sinn .........................................................
Trigonometrische Funktionen (Kreisfunktionen) .................................................
2.5.1 Die Eigenschaften der trigonometrischen Grundfunktionen ...................
2.5.2 Die allgemeine Sinusfunktion .................................................................
39
39
42
47
47
74
94
95
95
96
98
109
113
113
118
120
120
129
3 Folgen und Reihen ....................................................................................................... 133
3.1
3.2
Grundlagen ...........................................................................................................
3.1.1 Folge als Funktion ...................................................................................
3.1.2 Schreibweise von Folgen ........................................................................
3.1.3 Eigenschaften von Folgen .......................................................................
3.1.4 Reihen .....................................................................................................
Spezielle (endliche) Folgen ..................................................................................
3.2.1 Arithmetische Folgen und Reihen ...........................................................
3.2.2 Geometrische Folgen und Reihen ...........................................................
133
133
134
136
138
140
140
147
VIII
3.3
Inhaltsverzeichnis
Grenzwert von Folgen .......................................................................................... 155
3.3.1 Unendliche geometrische Folgen und Reihen ......................................... 155
*3.3.2 Verallgemeinerung des Grenzwertbegriffes ............................................ 162
4 Grenzwert von Funktionen – Stetigkeit ...................................................................... 165
4.1
Grenzwerte von Funktionen ..................................................................................
4.1.1 Erfordernis diverser Grenzwertbetrachtungen ........................................
4.1.2 Rechnerischer Umgang mit Grenzwerten ................................................
*4.1.3 Anwendung auf Kurvenuntersuchungen einfacher gebrochenrationaler Funktionen ..............................................................................
4.2 Stetigkeit ...............................................................................................................
4.2.1 Begriff der Stetigkeit ...............................................................................
4.2.2 Globale Stetigkeit ....................................................................................
165
165
169
176
183
183
186
5 Differentialrechnung ................................................................................................... 187
5.1
Das Tangentenproblem .........................................................................................
5.1.1 Die Differenzenquotientenfunktion .........................................................
5.1.2 Allgemeine Definition des Differentialquotienten ..................................
5.1.3 Einfache Differentiationsregeln ..............................................................
*5.1.4 Differenzierbarkeit und Stetigkeit ...........................................................
*5.1.5 Anwendung in der Physik .......................................................................
5.1.6 Newton’sches Näherungsverfahren .........................................................
5.2 Anwendung auf Kurvenuntersuchungen ..............................................................
5.2.1 Extremstellen von Funktionen – Krümmungsverhalten ..........................
5.2.2 Wendepunkte ...........................................................................................
5.2.3 Kurvendiskussion ganzrationaler Funktionen .........................................
5.2.4 Funktionssynthese ...................................................................................
5.3 Extremwertaufgaben mit Nebenbedingungen .......................................................
187
187
191
192
198
199
202
203
204
208
213
218
221
6 Integralrechnung ......................................................................................................... 228
6.1
Das bestimmte Integral .........................................................................................
6.1.1 Das Flächenproblem ................................................................................
6.1.2 Die Berechnung des bestimmten Integrals ganzrationaler Funktionen ...
*6.2 Die Integration als Umkehrung der Differentiation ..............................................
6.2.1 Stammfunktion und unbestimmtes Integral .............................................
6.2.2 Die Berechnung bestimmter Integrale mit Hilfe von Stammfunktionen .
228
228
238
251
251
254
7 Vertiefung der Differential- und Integralrechnung .................................................. 255
7.1
Weitere Differentiationsregeln ..............................................................................
7.1.1 Produktregel ............................................................................................
7.1.2 Quotientenregel .......................................................................................
7.1.3 Kettenregel ..............................................................................................
7.2 Kurvendiskussion gebrochen-rationaler Funktionen ............................................
7.3 Kurvendiskussion trigonometrischer Funktionen .................................................
7.3.1 Die Differentiation der trigonometrischen Grundfunktionen ..................
7.3.2 Zusammengesetzte trigonometrische Funktionen ...................................
255
255
256
257
261
273
273
278
Inhaltsverzeichnis
7.4
Exponentialfunktionen ..........................................................................................
7.4.1 Allgemeine Exponentialfunktionen .........................................................
7.4.2 Euler’sche Zahl und e-Funktion ..............................................................
7.4.3 Wachstum und Zerfall .............................................................................
7.4.4 Kurvendiskussion verknüpfter e-Funktionen ..........................................
*7.5 Krümmung und Krümmungsradius einer Kurve ..................................................
IX
281
281
283
289
293
296
Teil B: Analytische Geometrie .......................................................................................... 301
8 Vektoren ....................................................................................................................... 302
8.1
8.2
8.3
Grundlagen ...........................................................................................................
8.1.1 Skalare und vektorielle Größen ...............................................................
8.1.2 Der Vektorbegriff ....................................................................................
8.1.3 Eigenschaften von Vektoren ...................................................................
8.1.4 Vektoren im Anschauungsraum ..............................................................
Elementare Rechenoperationen ............................................................................
8.2.1 Vektoraddition und -subtraktion .............................................................
8.2.2 Multiplikation eines Vektors mit einem Skalar (S-Multiplikation) .........
Vektormultiplikationen .........................................................................................
8.3.1 Das Skalarprodukt ...................................................................................
8.3.2 Das Vektorprodukt ..................................................................................
8.3.3 Das Spatprodukt ......................................................................................
302
302
302
305
307
313
313
323
333
333
344
349
9 Vektorgeometrie .......................................................................................................... 352
9.1
9.2
Vektorgeometrie der Geraden ...............................................................................
9.1.1 Die vektorielle Geradengleichung in Parameterform ..............................
9.1.2 Lagebeziehungen von Punkt und Gerade ................................................
9.1.3 Schnittpunkt zweier Geraden ..................................................................
9.1.4 Abstand Punkt – Gerade ..........................................................................
9.1.5 Abstand windschiefer Geraden ...............................................................
Vektorgeometrie der Ebene ..................................................................................
9.2.1 Die vektorielle Ebenengleichung in Parameterform ...............................
9.2.2 Koordinatenform der Ebenengleichung ..................................................
9.2.3 Schnittpunkt Gerade – Ebene ..................................................................
9.2.4 Abstand Punkt – Ebene ...........................................................................
352
352
355
358
361
364
366
366
368
370
372
10 Komplexe Zahlen ......................................................................................................... 374
10.1 Grundlagen ...........................................................................................................
10.1.1 Zahlenbereichserweiterung von R auf C ................................................
10.1.2 Darstellung komplexer Zahlen ................................................................
10.2 Grundrechenarten .................................................................................................
10.2.1 Addition und Subtraktion komplexer Zahlen ..........................................
10.2.2 Multiplikation komplexer Zahlen ............................................................
10.2.3 Division komplexer Zahlen .....................................................................
374
374
375
376
376
377
378
Ausblick .............................................................................................................................. 379
Sachwortverzeichnis .......................................................................................................... 382
X
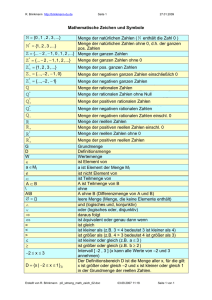
Mathematische Zeichen und Begriffe
1 Logik
:=
definitionsgemäß gleich; Kennzeichnung einer
Definitionsgleichung, bei welcher der zu definierende Begriff auf der Seite des Doppelpunktes steht.
∧
und (im Sinne von sowohl ... als auch)
∨
oder (im nicht-ausschließenden Sinn)
daraus folgt; wenn ..., dann
(p q: Aus p folgt q, d. h. p ist hinreichende
Bedingung für q und q ist notwendige Bedingung für p.)
⇔
äquivalent (gleichwertig); genau dann ..., wenn
(p ⇔ q: Aus p folgt q und umgekehrt)
2 Relationen zwischen Zahlen
a=b
a gleich b
a≠b
a ungleich b
a<b
a kleiner b
a>b
a größer b
a≤b
a kleiner oder gleich b
a≥b
a größer oder gleich b
a≈b
a ungefähr gleich b
ˆb
a=
a entspricht b (gebräuchlich z. B. bei Maßstabsangaben)
3 Mengen
A, B, C, ..., M, N, ...
Mengen
a ∈ M (M ∋ a )
a ist Element von M (M enthält a)
a∉M
a ist nicht Element von M
{a, b, c, d}
Menge mit den Elementen a, b, c und d
{x | ...}
Menge aller x, für die gilt ...
{x | ...}M
Menge aller x ∈ M, für die gilt ...
{}
leere Menge
A=B
A gleich B, d. h. x ∈ A ⇔ x ∈ B
A ⊂ B (B ⊃ A)
A ist (echte) Teilmenge von B: x ∈ A x ∈ B
und A ≠ B (B ist (echte) Obermenge von A)
A⊆B
A ist echte oder unechte Teilmenge von B
(d. h. A ⊂ B oder A = B)
Mathematische Zeichen und Begriffe
XI
A ⊆/ B
A ist nicht Teilmenge von B
A ∩ B := {x | x ∈ A ∧ x ∈ B}
A geschnitten B
Schnittmenge (Durchschnitt) von A und B
Technik: Zwei Schalter in Reihe geschaltet
A ∪ B := {x | x ∈ A ∨ x ∈ B}
A vereinigt B
Vereinigungsmenge von A und B
Technik: Zwei Schalter parallel geschaltet
B \ A := {x | x ∈ B ∧ x ∉ A}
:= {x | x ∉ A}B für A ⊆ B
A´B
A × B := {(x; y) | x ∈ A ∧ y ∈ B}
B ohne A; Differenzmenge von B und A
Ergänzungsmenge von A zu B, d. h. A ∪ A´B = B
A kreuz B; Paarmenge von A und B (kartesisches Produkt)
charakteristische Mengen
N:= {0, 1, 2, 3, ...}
Menge der natürlichen Zahlen
N* := N \ {0}
Menge der natürlichen Zahlen ohne 0
Z:= {..., – 1, 0, 1, 2, ...}
Menge der ganzen Zahlen
Z* := Z \ {0}
Menge der ganzen Zahlen ohne 0
Q:={
p
| p∈Z ∧ q∈Z*}
q
Menge der rationalen Zahlen
R
Menge der reellen Zahlen
:= {x | x ∉ Q}R
Menge der irrationalen Zahlen
R+
Menge der positiven reellen Zahlen
R 0+
:= R+ ∪ {0}
R– := R
\R 0+
Menge der positiven reellen Zahlen einschl. 0
Menge der negativen reellen Zahlen
R* := R \ {0}
Menge der reellen Zahlen ohne 0
C := {z| z = x + iy ∧ x, y ∈ R}
Menge der komplexen Zahlen
i=
imaginäre Einheit, definiert zu i2 = -1
−1
z = x + iy
z = x - iy
konjugiert-komplexe Zahlen
[a; b] := {x | a ≤ x ≤ b}R
geschlossenes Intervall
]a; b[ := {x | a < x < b}R
offenes Intervall
[a; b[ := {x | a ≤ x < b}R
]a; b] := {x | a < x ≤ b}R
|x| :=
+ x für x ∈ R 0+
– x für x ∈ R–
halboffene Intervalle
Betrag einer (reellen) Zahl x
XII
Mathematische Zeichen und Begriffe
4 Funktionen
→
Zahlen- und Mengenzuordnungspfeil
R
Relation als Teilmenge eines kartesischen Produkts
f (auch g oder h)
Funktion als Spezialfall einer Relation
f: x → f (x)
Funktionsvorschrift
f (x)
Funktionswert (Bild von x); aber auch Funktionsterm
y = f (x)
Funktionsgleichung
f:
D→W
x → f (x)
Funktion f mit Definitionsmenge D und Wertmenge W
f –1 (R–1)
Umkehrfunktion (Umkehrrelation)
Gf ∋ P
Graph von f (Punktmenge) mit dem Punkt P(x|y)
P(x|y)
Punkt der x, y-Ebene: R2-Ebene
P(x|y|z)
Punkt des (Anschauungs-) Raumes: R3
≡
Identitätszeichen („ist identisch gleich“); z. B.
Gerade g ≡ y = 2x-1
f ° g (g ° f )
Verknüpfungszeichen für verkettete Funktionen ( f nach g bzw. g nach f )
f ', f ", f '", ..., f (n)
1., 2., 3., ..., n-te Ableitungsfunktion von f
b
³ f ( x) dx
bestimmtes Integral der Funktion f über [a; b]
³ f ( x) dx
unbestimmtes Integral der Funktion f
F ( x) = ³ f ( x) dx
Stammfunktionen von f mit F '(x) = f (x).
a
5 Weitere Zeichen
(an)
Folge mit den Gliedern (a1, a2, ..., an, ...)
n
¦ ak
Summationssymbol: a1 + a2 + ... + an–1 + an
∞
unendlich
k =1
lim an
Grenzwert einer Folge für n gegen ∞
lim f ( x)
Grenzwert einer Funktion f für x gegen x0
n →∞
x→ x 0
Mathematische Zeichen und Begriffe
XIII
6 Zeichen aus der analytischen Geometrie
G G G G G G
a , b , c ,..., x , y , z
Vektoren
JJJG
G
G
v = AB
AB als Repräsentant von v
-v
Gegenvektor zu v
|v |
Betrag von v
G
G
G
G
G
G
G
v ° oder ev
Einheitsvektor in Richtung v
ex , e y , ez
Basisvektoren des R3
0
Nullvektor
G
G
G
G
G
Ortsvektor zu einem Punkt P : rP = OP
rP
⎛v ⎞
x
G ⎜ ⎟
G
v =⎜ v y ⎟
⎜ ⎟
⎝ vz ⎠
Spaltenschreibweise von v : Spaltenvektor
v = (v x , v y , v z )
Zeilenschreibweise von v : Zeilenvektor
a
a12
§ a11 a12 ·
¨¨
¸¸ bzw. 11
a21 a22
© a21 a22 ¹
2×2-Matrix bzw. 2-reihige Determinante
(a , b) = a ⋅b
Skalar- oder Punktprodukt
[a , b]= a × b
Vektor- oder Kreuzprodukt
G
G
GG
G G
GG
G G
GG G
Spatprodukt
a , b, c
G
G
G
G
G
G
x = r0 + λ⋅v
vektorielle Geradengleichung
G
x = r0 + λ⋅v + μ⋅ w
vektorielle Ebenengleichung
7 Wichtige Begriffe
Definition
Die Bedeutung eines verwendeten Namens
oder Zeichens wird erklärt bzw. festgelegt.
Satz
Unter Beachtung der Gesetze der Logik werden aus bereits bekannten Aussagen Schlussfolgerungen (Behauptungen) gezogen, die es
zu beweisen gilt. – Zur Beweisführung darf auf
Definitionen zurückgegriffen werden.
Axiom
Anerkannter, nicht beweisbarer Grundsatz, aus
dem sich Sätze ableiten lassen.
1
Teil A: Analysis
Eines der bedeutsamsten Gebiete der Mathematik ist die Analysis, unter der man ganz allgemein die Lehre von den Funktionen versteht. Ihre charakteristischen Methoden finden inzwischen1) mannigfaltig Anwendung in Wirtschaft, Wissenschaft und Technik; sie basieren auf
den Begriffen
Zahl, Funktion, Grenzwert.
Zahl und Funktion dürften aus vorangegangener Beschäftigung mit der Mathematik mehr oder
weniger gut bekannt sein und müssen nunmehr im Rahmen eines systematischeren Aufbaus
ergänzt und vertieft werden. - Elementare Funktionsuntersuchungen rücken dabei zunächst in
den Vordergrund der Überlegungen.
Mit dem Begriff Grenzwert, sowohl über Folgen als auch über Funktionen eingeführt, erschließt sich das Rechnen mit infinitesimalen Größen. Damit werden die Grundlagen geschaffen für die Differential- und Integralrechnung mit ihren grundlegenden Problemstellungen,
nämlich der Tangenten- und der Flächenproblematik und ihren verwandten Themenbereichen.
1)
d. h. seit dem 18. Jahrhundert
2
1 Die reellen Zahlen
1 Die reellen Zahlen
1.1 Die Grundeigenschaften der reellen Zahlen
1.1.1 Von den natürlichen zu den reellen Zahlen
Peter Hoeg hat es in „Fräulein Smillas Gespür für Schnee“ in schöner Prosa festgehalten:
„Weißt du, was hinter der Mathematik steckt? Hinter der Mathematik stecken die Zahlen. Wenn mich
jemand fragen würde, was mich richtig glücklich macht, dann würde ich antworten: die Zahlen. Schnee
und Eis und Zahlen. Und weißt du warum? …
Weil das Zahlensystem wie das Menschenleben ist. Zu Anfang hat man die natürlichen Zahlen. Das
sind die ganzen und positiven. Die Zahlen des Kindes. Doch das menschliche Bewusstsein expandiert.
Das Kind entdeckt die Sehnsucht, und weißt du, was der mathematische Ausdruck für die Sehnsucht
ist? …
Es sind die negativen Zahlen. Die Formalisierung des Gefühls, dass einem etwas abgeht. Und das Bewusstsein erweitert sich immer noch und wächst, das Kind entdeckt Zwischenräume. Zwischen den
Steinen, den Moosen auf den Steinen, zwischen den Menschen. Und zwischen den Zahlen. Und weißt
du, wohin das führt? Zu den Brüchen. Die ganzen Zahlen plus die Brüche ergeben die rationalen Zahlen. Aber das Bewusstsein macht dort nicht halt. Es will die Vernunft überschreiten. Es fügt eine so
absurde Operation wie das Wurzelziehen hinzu. Und erhält die irrationalen Zahlen. …
Es ist ein Wahnsinn. Denn die irrationalen Zahlen sind endlos. Man kann sie nicht schreiben. Sie zwingen das Bewusstsein ins Grenzenlose hinaus. Und wenn man die irrationalen Zahlen mit den rationalen
zusammenlegt, hat man die reellen Zahlen. …
Es hört nicht auf. Es hört nie auf. Denn jetzt gleich, auf der Stelle, erweitern wir die reellen Zahlen um
die imaginären, um die Quadratwurzeln der negativen Zahlen. Das sind Zahlen, die wir uns nicht vorstellen können. Zahlen, die das Normalbewusstsein nicht fassen kann. Und wenn wir die imaginären
Zahlen zu den reellen Zahlen dazurechnen, haben wir das komplexe Zahlensystem. Das erste Zahlensystem, das eine erschöpfende Darstellung der Eiskristallbildung ermöglicht. Es ist wie eine große, offene Landschaft. Die Horizonte. Man zieht ihnen entgegen, und sie ziehen sich immer wieder zurück.
…“ 1)
Die natürlichen Zahlen
Sie sind Grundlage für den Zahlenaufbau und gemäß DIN 1302 wie folgt definiert:
Menge der natürlichen Zahlen:
N: = {0, 1, 2, 3,...} .
Die wesentlichsten Merkmale dieser Zahlenmenge:
1. 0 ist die kleinste natürliche Zahl.
2. Zu jeder natürlichen Zahl n existiert ein eindeutig bestimmter Nachfolger n' = n + 1
(Also: 0' := 1 = 0 + 1; 1' := 2 = 1 + 1; 2' := 3 = 2 + 1; usw.)
3. Es gibt keine letzte (= größte) natürliche Zahl.
(Zu einer vermeintlich letzten natürlichen Zahl ließe sich wiederholt die 1 addieren.)
1)
Peter Hoeg, Fräulein Smillas Gespür für Schnee. Roman. Aus dem Dänischen von Monika Wesemann. © 1994 Carl Hanser Verlag, München.
1.1 Die Grundeigenschaften der reellen Zahlen
3
N ist angeordnet
Die natürlichen Zahlen sind gemäß Kleiner-Relation 1) geordnet: So ist z. B. 2 < 5 und 5 < 7,
was auf 2 < 7 schließen lässt.
Der in Bild 1.1 dargestellte Zahlenstrahl veranschaulicht die
Grundsätze, wobei die Pfeilrichtung das Größerwerden anzeigt.
Bild 1.1
¾ Eine wichtige Teilmenge von N ist die der positiv-ganzen Zahlen: N* = N\{0} = {1, 2, 3, ...}.
Meinungsstreit, die Zahl 0 betreffend
In der mathematischen Literatur findet sich auch, dass die Zahl 1 kleinste natürliche Zahl sei.
Um die Zahl 0 als neutrales Element der Addition einzubeziehen, wird entsprechend wie folgt
definiert: N0 = {0}∪{1, 2, 3, ...}= {0, 1, 2, 3, ...}.
Zur Klarstellung: Für die Beschäftigung mit der Mathematik ist es letztendlich unerheblich, ob
die Zahl 0 der Menge Nzugerechnet wird oder aber nicht; es ist einzig Definitionssache.
Sonderfall: Die Zahl 1
Sie ist neutrales Element der Multiplikation und erwirkt keine Veränderung eines Produktes.
N ist abgeschlossen
Die Summe und das Produkt zweier natürlicher Zahlen sind wieder natürliche Zahlen. Die
beiden Verknüpfungen „ + “ und „ · “ führen nicht aus N heraus.
Die Notwendigkeit von Zahlenbereichserweiterungen
Die Menge N bietet wenig Möglichkeiten, Rechenoperationen ohne Einschränkungen gelten
zu lassen. Algebraisch leistungsfähigere Zahlen müssen her, was prinzipiell wie folgt geschieht:
1. Der neue Zahlenbereich lässt sich mit Hilfe bereits definierter Zahlen beschreiben.
2. Die für die ursprünglichen Zahlen formulierten Grundsätze gelten auch in der erweiterten
Zahlenmenge (Permanenzprinzip).
3. Für den erweiterten Zahlenbereich werden – soweit nötig – zusätzliche, widerspruchsfreie
Axiome formuliert.
Ganze Zahlen
Die Einführung der negativ-ganzen Zahlen mit Z– := {x | x = – n ∧ n ∈ N*}
ermöglicht die Zahlenbereichserweiterung von N zur
Menge der ganzen Zahlen:
Z:= Z– ∪ N
, also Z = {..., – 3, – 2, – 1, 0, 1, 2, 3, ...}.
N und Z– sind ebenso in Z enthalten wie die positiv-ganzen Zahlen2) mit Z+ = N*.
Erwähnenswert sind ferner Z 0+ := Z+ ∪ {0} (= N), Z 0− := Z– ∪ {0} und Z * := Z \ {0} .
1)
2)
von relatio (lat.): Beziehung
somit gilt + n = n (n ∈ N*)
4
1 Die reellen Zahlen
Entsprechend gilt Z = Z+ ∪ Z– ∪ {0},
was Bild 1.2 veranschaulicht.
Bild 1.2 Z: = Z+ ∪ Z– ∪ {0}
¾ Sonderformen 1)
Z + steht für die nicht-negativen ganzen Zahlen incl. der Zahl 0 und Z *+ := Z + \ {0}.
Z ist angeordnet
Zu jeder positiv-ganzen Zahl n existiert eine negativ-ganze Zahl – n mit n + (–n) = 0.
Bild 1.3 zeigt die orientierte Zahlengerade und veranschaulicht das Größerwerden:
Je weiter die Zahlen links von der 0 stehen, desto kleiner sind sie,
je weiter sie rechts davon angeordnet sind, desto größer werden sie.
Bild 1.3 Z ist angeordnet
Rationale Zahlen
Die ganzen Zahlen leisten algebraisch mehr als die natürlichen Zahlen. Aber auch mit ihnen ist
es nicht möglich, für Gleichungen wie z. B. 2x = 3 eine Lösung anzugeben. Bruchzahlen werden benötigt (Quotient, bestehend aus Zähler und Nenner), was eine nochmalige Zahlenbereichserweiterung erfordert:
⎧p
⎫
Menge der rationalen 2) Zahlen mit Q = ⎨ p ∈ Z ∧ q ∈ Z *⎬ .
⎩q
⎭
Die Elemente von Z sind in Q enthalten, was die folgenden Beispiele zeigen:
Beispiele: 2 = +2 = +4 = ... = −2 = ...; − 3 = +3 = −3 = ...
+1
+2
−1
−1
+1
Wie die ganzen Zahlen lassen sich auch die rationalen Zahlen weiter unterteilen, und zwar in
– negativ-rationale Zahlen, bezeichnet mit Q– und
– positiv-rationale Zahlen, bezeichnet mit Q+.
Folglich gilt Q :=Q+ ∪Q– ∪ {0}, also ist auch 0∈ Q .
Die Null kann in der Form
0
q
mit q ∈ Z* geschrieben werden.
Erwähnenswert sind ferner Q 0− :=Q– ∪ {0}, Q 0+ :=Q+ ∪ {0} sowie Q* :=Q \ {0} .
¾ Sonderformen 3)
Q + steht für die nicht-negativen rationalen Zahlen incl. der Zahl 0 und Q *+ := Q + \ {0}.
1)
2)
3)
Sie sind nach DIN 5473 auch zugelassen, werden in diesem Rahmen jedoch nicht verwandt.
ratio (lat.): Vernunft, Verstand, aber auch Verhältnis
wie 1)
1.1 Die Grundeigenschaften der reellen Zahlen
5
Konstruktion rationaler Zahlen
Wie Q aus der Menge N bzw. Z hervorgeht, veranschaulicht Bild 1.4:
Mittels 1. Strahlensatzes wird exemplarisch der Bildpunkt der rationalen Zahl r =
2
3
konstruiert.
¾ Q ist gemäß Permanenzprinzip angeordnet1).
Bild 1.4
Konstruktion der rationalen Zahl r =
2
3
Q ist dicht
1. Keine rationale Zahl weist einen unmittelbaren Vorgänger oder Nachfolger auf.
2. Zwischen zwei rationalen Zahlen (a < b) existiert mindestens eine weitere rationale Zahl
r=
a+b
mit a < r < b gemäß Bild 1.5.
2
Bild 1.5
a<
a+b
<b
2
Also: Zwischen zwei verschiedenen rationalen Zahlen existieren unendlich viele weitere davon.
¾ Die Elemente vonQ liegen dicht2).
Der Kehrwert
Zu jeder Zahl r∈Q* existiert eine reziproke Zahl (= Kehrwert)
mit der Eigenschaft
r⋅
1
=1
r
.
Hinweis: Für
1
r
1
r
∈ Q*
wird auch r –1 geschrieben.
Achtung: Im Nenner eines Bruches darf die Zahl 0 nicht auftreten(ĺ Definition vonQ).
Dieses „Teile niemals durch 0“ wird „roter Faden“ bis hin zur Differentialrechnung sein.
¾ Q ist nullteilerfrei.
Beispiel:
Es sei x = 1 x2 = 1 ⇔ x2 – 1 = x – 1
Faktorisieren des linken Terms: (x – 1) (x + 1) = x – 1
Division mit (x – 1):
x+1=1
x = 0.
(Somit wäre 1 = 0, oder ...?)
1)
2)
Man beachte: – 1 < – 1/1000
Die Elemente von Z liegen nicht dicht; denn es gibt z. B. zwischen 1 und 2 keine weitere ganze Zahl.
6
1 Die reellen Zahlen
Dezimalbrüche als rationale Zahlen
Für eine nochmalige Zahlenbereichserweiterung werden vorab Dezimalbrüche betrachtet:
a) endliche Dezimalbrüche
Die dekadische Schreibweise kann nicht verunsichern: Endliche Dezimalbrüche lassen sich
exakt in Form eines Bruches schreiben und ggf. so weit kürzen, dass Zähler und Nenner
keinen gemeinsamen Teiler mehr haben.
1
1
1
Beispiele: 0,5 = 5 = ; 0,25 = 25 = ; 0,125 = 125 = .
10
2
100
1000
4
8
b) unendliche periodische Dezimalbrüche
Ein klassisches Beispiel ist die Dezimalzahl 0,333 …, was kürzer durch die Schreibweise
0, 3 (gelesen: 0 Komma Periode 3) angegeben wird.
Sie lässt sich gemäß Bild 1.6 einschachteln durch endliche Dezimalbrüche:
0
<
0,3
<
0,33
<
0,333 <
1
3
1
3
1
3
1
3
<l
< 0,4
< 0,34
< 0,334 usw.
Bild 1.6 Einschachtelung der rationalen Zahl
Problem: Steht 0, 3 exakt oder annähernd für die rationale Zahl
Heißt es also korrekt
0, 3 =
1
3
oder 0, 3 ≈
1
3
1
3
1
?
3
?
Multiplikation mit Faktor 3 liefert 0, 9 = 1 bzw. 0, 9 ≈ 1,
was Veranlassung sein mag, dem ungefähr gleich (≈) zuzuneigen.
Dass dem nicht so ist, zeigt nachfolgende Rechnung:
Aus r = 0, 3 folgt
10r = 3, 3 ; eine Subtraktion lässt die Periode verschwinden:
r = 0, 3 −
1
1
; d. h. ∈ Q.
3
3
¾ Fazit: Jeder unendliche periodische Dezimalbruch ist eine rationale Zahl.
9r = 3 r =
c) unendliche nicht-periodische Dezimalbrüche
Es sei vorweggenommen: Sie gehören nicht zuQ.
Grund genug, den Zahlenbereich nochmals zu erweitern.
Irrationale Zahlen
Die dicht liegenden Bildpunkte rationaler Zahlen füllen die Zahlengerade nicht vollständig
aus. Das lässt sich konkret anhand der algebraischen Gleichung x2 = 2 zeigen.
1.1 Die Grundeigenschaften der reellen Zahlen
7
2 (bzw. – 2 ) sind Lösungen dieser Gleichung. Der vom ET-Rechner für 2 ausgewiesene endliche (!) Dezimalbruch stellt nur eine Näherung dar, das dürfte klar sein. Inwieweit
dieser sich abzuzeichnende unendliche Dezimalbruch irgendwann einmal periodisch werden
könnte und damit der Menge Q zuzurechnen wäre, ist bisher noch ungeklärt.
Das Prinzip der Einschachtelung , wie für r =
1
3
angewandt,
lässt vermuten, 2 letztendlich exakt in Form eines Bruches
schreiben zu können.
<
2 <2
1,4
<
2 < 1,5
1,41
<
2 < 1,42
<
2 < 1,415
1,414
usw.
Dass dem nicht so ist, kann bewiesen werden.
Indirekter Beweis1) zu
1
2∉Q
Annahme: Es gibt für x2 = 2 doch eine rationale Variable x als Lösung.
Schreiben lässt sich das in der Form
2
§ p·
2)
x 2 = ¨¨ ¸¸ = 2 , wobei p ∈ Z u. q ∈ Z*, ferner p und q teilerfremd zueinander sind.
©q¹
Dann gilt
p2
q2
= 2 p2 = 2q2; Faktor 2 zeigt, dass p2 und damit p eine gerade Zahl ist,
also: p = 2r, r ∈ Z*.
Eingesetzt: (2r)2 = 2q2 ⇔ 2r2 = q2, somit wäre wegen des Faktors 2 auch q eine gerade Zahl.
Das steht im Widerspruch zu der Annahme, p und q seien teilerfremd zueinander.
Die eingangs aufgestellte Behauptung, x sei eine rationale Zahl, kann nicht richtig sein:
x ist irrational, d. h. nicht-rational.
¾ Irrational nennt man Zahlen, die nicht exakt in Form eines Bruches p/q darstellbar sind.
Konstruktion von 2
Der irrationalen Zahl 2 kann genau ein
Punkt auf der Zahlengeraden zugeordnet werden. Die Konstruktion (Bild 1.7) basiert auf
dem Lehrsatz des Pythagoras3):
( 2 )2 = 12 + 12.
Bild 1.7 Konstruktion der irrationalen Zahl
1)
2)
3)
2
Prinzip: Das Gegenteil der zu beweisenden Behauptung als wahr anzusehen und daraus einen Widerspruch abzuleiten.
Der Quotient p/q ist so weit wie möglich gekürzt.
benannt nach Pythagoras (um 570 v. Chr. – 497/96 v. Chr.); griech. Philosoph
8
1 Die reellen Zahlen
Diese Überlegungen sind übertragbar auf irrationale Zahlen wie 3 ,
(p: Primzahl)
1)
5 und allgemein
p
sowie auf die entsprechend negativen Wurzelwerte.
Noch allgemeiner: Das Symbol
a mit a∈ N*\{1} steht genau dann für eine irrationale Zahl,
wenn nicht a das Quadrat einer rationalen Zahl ist ( 9 ∈ Q; denn 9 = 3).
Weitere Beispiele für irrationale Zahlen
a) Zahlen der Form
n
a mit n ∈ N*\{1} und a ∈ Q+, z. B.
3 5, 4 10, 5
27 usw.
Gegenbeispiele: 3 27 , 5 32 usw.
b) die Zahl π ≈ 3,14159... (andere Näherung: π ≈
c)
355
113 );
die Zahl e ≈ 2,71828 ... (ĺ Kapitel 7, Abschnitt 7.4.2);
d) Logarithmen, z. B.
lg 22), definiert als diejenige (positive) Hochzahl, für die gilt 10lg2 = 2;
lb 33), definiert als diejenige (positive) Hochzahl, für die gilt 2lb3 = 3;
ln 44), definiert als diejenige (positive) Hochzahl, für die gilt eln4 = 4;
Gegenbeispiele: lg 100 = 2 ⇔ 102 = 100, lb 8 = 3 ⇔ 23 = 8 u.a.;
e) trigonometrische Funktionswerte wie sin r ⋅ π , cos r ⋅ π , tan r ⋅ π , cot r ⋅ π , wobei r∈Q;
Beispiele: sin
π 1
π 1
π
= ⋅ 2 , cos = ⋅ 3 , tan =
4 2
6 2
3
Gegenbeispiele: sin
3 , cot
π 1
=
6 3
⋅ 3 u.a.
π 1
π
π
= , cos 0 ⋅ π = 1, tan = 1, cot = 0 u.a.
6 2
4
2
¾ Die irrationalen Zahlen bilden in ihrer Gesamtheit die Menge .
Reelle Zahlen
Die Existenz irrationaler Zahlen bestätigt es: Die Zahlengerade mit den dicht angeordneten
rationalen Zahlen ist nicht vollständig ausgefüllt; es bestehen Lücken.
Um diese zu beseitigen, werden rationale und irrationale Zahlen zusammengefasst zur
Menge der reellen Zahlen: R := Q ∪ Das Einschachtelungsprinzip, exemplarisch gezeigt für 0, 3 und
jede reelle Zahl. Entsprechend erfolgt ihre Definition.
2 , ist charakteristisch für
Definition 1.1
Zahlen, durch Intervallschachtelung rationaler Zahlen bestimmt, heißen reelle Zahlen.
¾ Q und ergänzen sich zu R: Die reellen Zahlen füllen die Zahlengerade vollständig aus.
1)
2)
3)
4)
Primzahlen p ∈ N*\ {l} sind Zahlen, die genau zwei Teiler haben, nämlich sich selbst und die 1.
log n := log10 n (dekadischer Logarithmus)
lb n := log2 n (binärer Logarithmus)
ln n := loge n (natürlicher Logarithmus); e ≈ 2,71828… wird Euler’sche Zahl genannt
1.1 Die Grundeigenschaften der reellen Zahlen
9
Bild 1.8 R:= Q ∪ 1)
Bild 1.9 Übersicht über die Zahlenbereiche
Es gilt N ⊂ Z ⊂ Q ⊂ R, was sich anhand von Bild 1.9 zeigt.
Weitere Teilmengen von R sind
die positiven reellen Zahlen R+ := {x | x > 0}R,
die negativen reellen Zahlen R– := {x | x < 0}R,
ferner R 0+ := R+ ∪ {0}, R 0− := R– ∪ {0} und R* := R \{0} .
¾ Sonderformen 2)
R + steht für die nicht-negativen reellen Zahlen incl. der Zahl 0 und R *+ := R + \ {0}.
Anmerkung
Jede irrationale Zahl lässt sich durch rationale Zahlen beliebig genau annähern (z. B. 2 ≈ 1,414 oder
π ≈ 3,14159). Für die praktische Mathematik ist die Existenz irrationaler Zahlen und die damit verbundene Zahlenbereichserweiterung von Q auf R ohne Bedeutung. – Der Hinweis auf den Zahlentyp
Real (= Q) in der PC-Anwendung mag die Ausführungen bekräftigen.
Arithmetische Eigenschaften der reellen Zahlen
Die Gesetzmäßigkeiten bezüglich der Verknüpfungen „ + “ und „·“ sind diese:
1. R ist abgeschlossen,
2. besitzt ein neutrales Element der Addition (=0) und der Multiplikation (=1),
3. weist
– zu jeder Zahl r ∈ R ein additiv-inverses3) Element – r ∈ Rauf mit r + (– r) = 0 und
1
=1.
– zu jeder Zahl r* ∈ R* ein multiplikativ-inverses Element 1/r* mit r * ⋅
r*
4. Kommutativ-, Assoziativ- und Distributivgesetz gelten.
Hinweis: Diese Struktur wird auch algebraischer Körper genannt.
Der Wichtigkeit halber wird Position 4 aufgeschlüsselt:
1)
2)
3)
Q und sind disjunkt (= elementefremd) zueinander: Keine reelle Zahl ist rational und irrational.
Sie sind gemäß DIN 5473 auch zugelassen, werden in diesem Rahmen jedoch nicht verwandt.
invers (lat.): umgekehrt