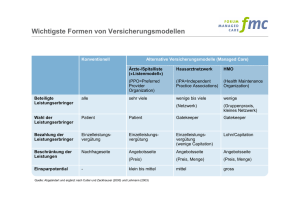
Grundlagen

Vorraussetzungen der Modellierung
Nachfrageseite:
I
I
I
I
Nutzenmaximierung
Nachfragefunktion
Wohlfahrt
partielles Gleichgewicht
Angebotsseite:
1. Modellierung von Firmen
I
I
Verhalten
Kostenfunktionen
2. Wettbewerbsumfeld
I
I
I
vollständige Konkurrenz: sehr viele Firmen
Monopol: eine Firma
unvollständige Konkurrenz: wenige Firmen (Oligopole)
1 / 33
Nachfragefunktion
Nachfrage: viele Käufer die sich nicht strategisch verhalten
können (Konsumenten, eventuell Zwischenhändler und
Inputfaktormärkte), d.h. sie sind Preisnehmer
diese Konsumenten verhalten sich rational und versuchen ihren
Nutzen zu maximieren ( utility maximising behaviour“)
”
das Resultat daraus wird durch eine Nachfragefunktion
beschrieben; häufig verwendet wird die einfache lineare Form
2 / 33
Wiederholung Haushaltstheorie
Ausgangspunkt: Haushalte haben Präferenzen über Güter; die
Präferenzen müssen bestimmte weitere Annahmen erfüllen; im
wesentlichen: Güterbündel für jede Person lassen sich stetig ordnen
als besser oder gleich gut; seien x und y zwei k-dimensionale
Güterbündel (Vektoren) bestehend aus den Mengen jeden Gutes
als Einträge, x 6= y ; x wird bevorzugt gegenüber y sei ausgedrückt
durch x y
die Annahmen erlauben, dass die Präferenzen einer Person durch
eine Funktion dargestellt werden, die Nutzenfunktion“ genannt
”
wird; das ist sehr praktisch für analytische Zwecke, z.B. Herleitung
einer Nachfragefunktion xi = xi (pi ) für ein Gut xi .
Die Nutzenfunktion u ordnet jedem Güterbündel eine Rangzahl zu:
u : X → R. Die Rangzahl spiegelt die Präferenzen insofern wider,
dass einem besseren Bündel ein höherer Wert zugeschrieben wird:
x y ⇔ u(x) > u(y ).
3 / 33
Indifferenzkurve
Eine einzelne Indifferenzkurve, die ein konstantes Nutzenniveau
aufweist:
{x|u(x) = ū}
aber es gibt Beschränkungen für die Auswahlmöglichkeiten: Güter
muss man bezahlen;
4 / 33
Budgetbeschränkung
Mittel sind beschränkt, für den Haushalt das Budget“, w . Die
”
Beschränkung ist:
w=
X
pi xi .
L
Gesamtausgaben für Bündel x bei Preisen p dürfen Budget
(Einkommen) w nicht überschreiten; 2-Güter-Fall:
5 / 33
Entscheidung unter Nebenbedingung
Wie kann Nutzen u(x) möglichst groß werden, gegeben Güterpreise
p und Einkommen w ?
Budget liegt fest bei w , alles darauf und darunter ist leistbar; je
weiter ein Nutzenniveau (Indifferenzkurve) weg vom Ursprung,
desto besser; höchstes leistbares Nutzenniveau ist das Optimum
6 / 33
Nachfragekurve: Graphische Herleitung
Ein Individuum gibt das Budget für 2 Güter aus, Bier und Wein.
Bierpreis sei ursprünglich pb0 = 12, pb sinkt dann.
Abbildung zeigt, wie sich
Optimum wegen
Preisänderung ändert.
Nachfrage nach Bier steigt,
wenn der Preis sinkt.
7 / 33
Nachfragefunktion
so erhält man für jedes Gut eine Nachfragefunktion
xi = xi (w , p1 , . . . , pi , . . . , pk );
sie hängt ab vom Einkommen, w , und vom Preisvektor p aller
Güter, insbesondere auch vom Preis des Gutes selbst, pi
8 / 33
Nachfragefunktion und Wohlfahrt
wenn Firmen als Ziel die Maximierung ihrer Profite verfolgen, kann
man veschiedene Situationen leicht dadurch vergleichen, dass man
die Höhe der Profite vergleicht, etwa bei einem Monopol
gegenüber freiem Wettbewerb (unten mehr dazu)
für Konsumenten/Haushalte kann man sich etwas ähnliches
überlegen
9 / 33
Nachfragefunktion und Wohlfahrt
sei Gut i ein Gut das in diskreten (ganzen) Einheiten verkauft wird;
Nachfrage:
(1) geordnete Zahlungsbereitschaft für jedes Stück
(2) Differenz zw. Zahlungsb. und Marktpreis p0 ist eine
pro-Stück-Rente für die Konsumenten, die graue Fläche die
gesamte Konsumentenrente
(3) rechts die Konsumentenrente beim Übergang zur
kontinuierlichen Nachfragekurve; wird (oft) als Wohlfahrtsmaß
verwendet
10 / 33
Veränderung der Konsumentenrente
interessant sind meistens Wohlfahrtsvergleiche; z.B. werde der
Markt zu einem Monopol und der Preis dadurch höher; wie
verändert sich die Situation für die Konsumenten?
Wohlfahrt auf diesem Markt hat sich verändert, und die
Veränderung wurde richtig berechnet, weil alles andere “ konstant
”
geblieben ist:
x10 = x1 (w , p10 , p2 , . . . , pk ),
x1M = x1 (w , p1M , p2 , . . . , pk )
11 / 33
Partielles Gleichgewicht
obige Herangehensweise berücksichtigt aber das neue
Gleichgewicht nur partiell“; die Nachfrage auf den anderen
”
Märkten verändert sich (außer unter sehr speziellen
Nachfragebedingungen, d.h. Nutzenfunktionen):
Konsumentenrente auf anderen Märkten verändert sich; das wird
in den in der LV verwendeten Analyse partieller Gleichgewichte“
”
aber vernachläßigt; bzw. die Annahme getroffen, dass diese Effekte
sehr klein“ sind
”
12 / 33
Nachfragekurve
Nachfragefunktion X (p) beschreibt wie groß die nachgefragte
Menge X ist, gegeben den Preis p. Z.B. linear:
I
X (p = 0): Sättigungsmenge; Bsp.: X (p = 0) = d
I
X (p) = 0: p ist der Prohibitivpreis; Bsp.:
X (p) = 0 = d − ep ⇔ p = de
I dX :
dp
Mengeneinheiten, um die sich Nachfrage erhöht wenn sich
p um eine Einheit erhöht; Bsp.: dX
dp = −e
13 / 33
Nachfragefunktion
Anstatt der Ableitung der Nachfrage ist manchmal die
mengeneinheitenunabhängige Preiselastizität informativer:
∆X
X ∆p→0
→
∆p
p
dX p
= X ,p
dp X
Interpretation: gibt die Prozent der Veränderung der Menge an,
pro Prozent Veränderung des Preises
X ,p =
dX p
dp X
p
= −e d−ep
14 / 33
Angebotsseite: Firmenverhalten
Modellierung von Firmen:
I
Als Ziel der Eigentümer wird die Maximierung der Profite
gesehen ( powerful representation as rational profit
”
maximisers“)
I
Firma wird als einzelner Entscheidungsträger betrachtet; die
einfachste Vorstellung ist die eines Eigentümer-Managers, bei
dem die Interessen einer Firma einheitlich sind und nicht etwa
das Management eigene Interessen verfolgt, die dem Ziel der
Eigentümer abträglich sind
15 / 33
Angebotsseite: Firmenverhalten
Zielkonflikte:
I
Hauptproblem ist die unvollständige Kontrolle über das
Verhalten des Managements
I
das führt dazu, dass z.B. zu wenig Anstrengung erbracht wird
um möglichst hohe Gewinne zu machen, oder zu schnelles
Wachstum verfolgt wird um eine möglichst große Firma zu
beherrschen (empire building, gut für Manager), usw.
I
Principal-Agent-Modelle befassen sich mit diesen
Zielkonflikten
16 / 33
Angebotsseite: Firmenverhalten
Auch bei der Zulassung von Principal-Agent-Problemen gibt es
Argumente, die die Annahme der Profitmaximierung plausibel
machen; z.B.:
I
Reputation von Managern und deren zukünftige Löhne
I
Beschränkung durch den Markt für Unternehmenskontrolle“
”
(market for corporate control): jemand der bei besserer
Leitung höhere Gewinne erwartet kann die schlecht geleitete
Firma aufkaufen und das Management ersetzen; das ist
gewinnbringend; Management muss sich anstrengen, da es
sonst den Job sofort wieder verliert
I
evolutionäre Perspektive: nur die Firmen die am besten
geführt werden können langfristig am Markt überleben
17 / 33
Angebotsseite: Abgrenzung der Firma
Abgrenzung der Aktivitäten einer Firma ( boundaries of the firm“)
”
wird ebefalls als gegeben betrachtet. In einer allumfassenden“
”
Darstellung müßte das auch berücksichtigt werden. Grundlegende
Fragestellungen sind:
I
Wie groß darf eine Firma werden, um nicht den Schwächen
einer planned economy“ zu erliegen? (Ronald Coase, NP
”
1991)
I
Wann führen wiederholte Transaktionen zwischen zwei Firmen
oder spezielle Abnahmeverträge zu Firmenverbindungen, und
wann bleiben sie getrennt? (Oliver Williamson, NP 2009)
18 / 33
Angebotsseite: Abgrenzung der Firma
Allerdings sind einige der Modelle für unvollständigen Wettbewerb
tatsächlich relevant für diese Frage der Firmenabgrenzung:
I
Verbundvorteile (economies of scope) für Mehrproduktfirmen
I
Verkaufsstrategien, wie das Bündeln bestimmter Produkte
(Microsoft Windows und Office)
I
Firmenverbindungen (Mergers und Acquisitions) um
Marktmacht von Inputfaktormärkten (upstream) oder
Vertriebsmärkten (downstream) zu übernehmen
Im Kurs werden wir diese Fragen höchstens streifen. Die
Abgrenzung der Firmen wird meist als exogen betrachtet.
19 / 33
Produktionsprozess: Bsp. Mikrochipherstellung
I
Halbleiterhersteller kaufen Siliciumscheiben (Wafer), und
tragen mehrere Schichten darauf auf (. . . ); um die Schichten
genau übereinander zu bringen, gibt es drei Möglichkeiten:
1. Aligner : mit dem Mikroskop werden die Schichten von
einem Arbeiter in die richtige Position gebracht;
arbeitsintensiv, ermöglicht 250 Schichten pro Tag (25
10-Schichten Chips)
2. Stepper : Schichten werden automatisch positioniert; ein
Arbeiter kann 2 Stepper bedienen, 500 Schichten pro Tag
produzierbar
3. Stepper mit Wafer-Führungsanlage: automatische Führung
zu den Steppern, sehr kapitalintensiv, am wenigsten
arbeitsintensiv; ein Arbeiter kann 4 Maschinen bedienen und
1000 Schichten pro Tag produzieren
(Perloff, J., Microeconomics, 2004, S. 163)
20 / 33
Isoquante: Illustration für Mikrochips
I
alle 3 Arten verwenden K und L in fixen Proportionen; für 200
q200,1 q200,2 q200,3
Chips braucht man:
(Li ,Maschinei ) (8,8) (3,6) (1,4)
I
manche Firmen verwenden Kombinationen und produzieren
entlang der Linien; mit der Erfindung neuer Prozesse wird die
Isoquante immer glatter“
”
21 / 33
Stetige Isoquante
Analog zur Haushaltstheorie unterstellt man die Existenz einer
stetigen Produktionsfunktion:
22 / 33
Minimalkostenkombination
ebenfalls ähnlich wie in der Haushaltstheorie nimmt man an, die
Firmen minimieren die Kosten, gegeben ein Outputniveau:
r1 und r2 sind die Kosten der Inputfaktoren; die parallelen Geraden
stellen Isokostenlinien“ dar, d.h. Inputfaktorkombinationen, die
”
die gleichen Kosten verursachen
23 / 33
Angebotsseite: Produktionsprozess
die verfügbaren Technologien ordnen den Inputfaktoren
Outputmengen zu; das wird in der Produktionsfunktion
zusammengefasst:
q = q(x1 , ..., xm )
das Optimierungsproblem, dass die Firmen lösen:
min(C = x1 r1 + . . . + xm rm ) s.t. q = q(x1 , ..., xm )
x
minimiere die Kosten C , die von der Outputhöhe q und den
Inputfaktorpreisen rj , j = 1, . . . , m abhängen, gegeben die
technologischen Möglichkeiten, die durch die Produktionsfunktion
q(·) beschrieben werden; wähle x optimal
24 / 33
Angebotsseite: Produktionsprozess
daraus resultiert eine Kostenfunktion, die jedem Vektor von Preisen
eine eindeutige kostengünstigste Inputfaktorkombination zuordnet,
gegeben man möchte Outputniveau q erreichen; diesen Prozess
betrachten wir als gegeben und verwenden nur das vereinfachte
Resultat:
C (q, r1 , ..., rm ) = C (q)
wenn die Firmen verschiedene Kostenfunktionen haben, dann ist
die Kostenfunktion von Firma i: Ci (qi ).
25 / 33
Vollkommene Konkurrenz
Vollkommener Wettbewerb: grundlegendes Modell des Marktes;
Annahmen sind:
I
viele Käufer und viele Verkäufer (sodass beide keinen“
”
Einfluß auf den Marktpreis p haben)
I
homogene (identische) Produkte
I
vollkommene Information über Preise und Homogenität der
Produkte
I
keine Transaktionskosten
I
Markteintritt und -austritt ist jederzeit möglich
Daher: Produzenten kalkulieren unter der Annahme eines fixen
Marktpreises p. Sinnvoll z.B. für Agrarmärkte.
26 / 33
Angebotsseite: Vollkommene Konkurrenz
vollkommene Konkurrenz ( perfect competition”): erster
”
Extremfall“ eines Wettbewerbsumfelds; kann auch als Spezialfall
”
der strategischen Interaktion gesehen werden;
grundlegende Annahme: die Firmen wissen nicht, dass ihr
Verhalten sich auf die anderen auswirkt und verhalten sich daher
nicht strategisch; tatsächlich ist ihr Einfluß auf den Markt auch
äußerst klein, weil es so viele von ihnen gibt; konkret: Preis wird
von Firmen als exogener Parameter betrachtet, daher ihr
Maximierungsproblem
max (Π(x) = px − C (x))
x
27 / 33
Angebotsseite: Vollkommene Konkurrenz
FOC:
!
dΠ(x)/dx = p − MC (x) = 0 ⇒
p = MC (x)
Preis gleich Grenzkosten” ist hier ein Spezialfall von Grenzerlös
”
”
gleich Grenzkosten”
Beachte: p = MC (q) ist daher eine individuelle (inverse)
Angebotsfunktion. Die individuell Angebotsfunktion für diese
Firma i ist q = Si (p)
28 / 33
Graphische Darstellung
29 / 33
Vollkommene Konkurrenz in der Kurzen Frist
Beachte: Produktionsentscheidung festgelegt ( Kapitalstock
”
fixiert“), Anzahl der Firmen fixiert; seien alle Firmen identisch:
SGES = S1 (p) + S2 (p) + . . . + SN (p) =
N
X
Si (p) = N · Si (p).
i=1
30 / 33
Vollkommene Konkurrenz in der Langen Frist
langfristig treten mehr und mehr Firmen in den Markt ein, solange
es positive (ökonomische) Gewinne gibt; gibt es sehr (sehr) viele
Firmen, dann wird die Angebotskurve annähernd horizontal
alternativ: es gibt ein Durchschnittskostenminimum, das alle
Firmen als Preis setzen müssen, um am Markt bestehen zu
können; ebenfalls (annähernd) horizontale Angebotskurve
31 / 33
Angebotsseite: Monopol
Monopol: entgegengesetztes Extrem eines Wettbewerbumfelds; es
gibt nur einen einzigen Anbieter am Markt; genaueres im nächsten
Kapitel;
32 / 33
Angebotsseite: Unvollständige Konkurrenz
unvollständige Konkurrenz: einige wenige Firmen (Duopol,
Oligopole) bedienen den Markt; dieser Fall liegt zwischen
vollständiger Konkurrenz und Monopol; strategische Interaktionen
werden relevant,
I
weil es, nicht wie im Monopol, mehrere Firmen gibt, also das
eigene Verhalten Auswirkungen auf die anderen Firmen hat
I
es nur so wenige Firmen gibt, dass das individuelle Verhalten
einer Firma eine Auswirkung auf den Markt hat und daher
auch auf die anderen Firmen; diese berücksichtigen daher das
Verhalten jeder anderen Firma; strategische Interaktionen
werden relevant
der Fall der unvollständigen Konkurrenz ist die interessante
Situation, die die Basis der Modelle für strategisches Verhalten des
Kurses bildet; Monopol und vollständige Konkurrenz werden als
Referenzfälle immer wieder zum Vergleich herangezogen
33 / 33