Lösungsvorschläge zu Blatt 3: 10) x1 x2 x3 -1 0 3 -2 -6 10 0 6 1

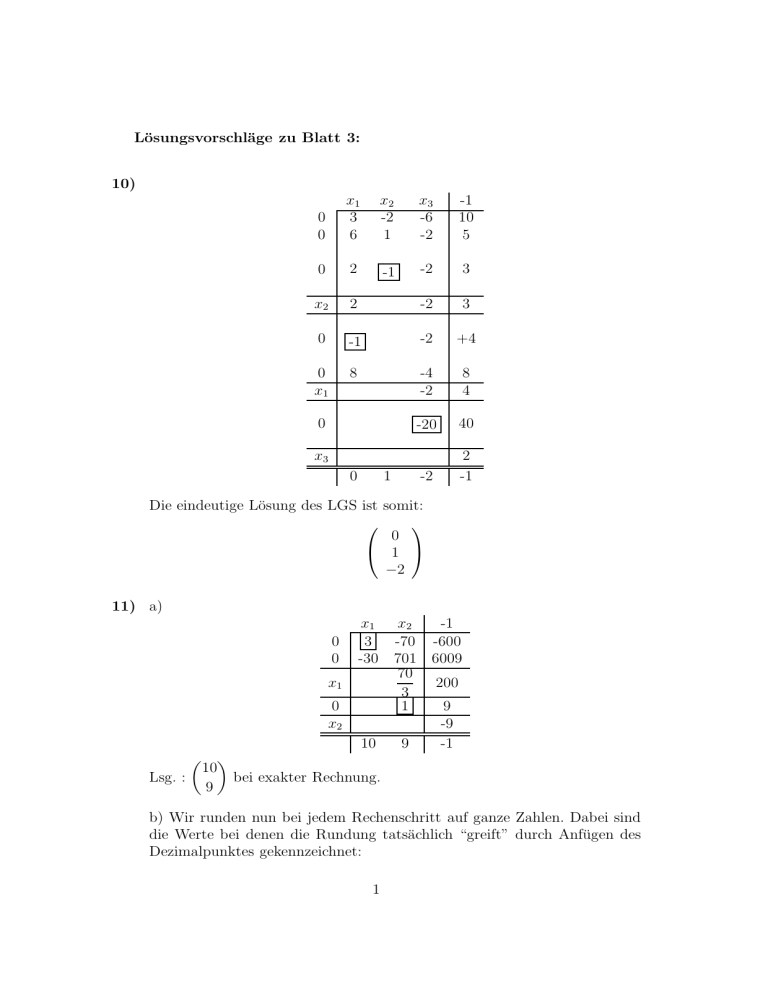
Lösungsvorschläge zu Blatt 3:
10)
0
0
x1
3
6
x2
-2
1
x3
-6
-2
-1
10
5
0
2
-1
-2
3
x2
2
-2
3
0
-1
-2
+4
0
x1
8
-4
-2
8
4
-20
40
-2
2
-1
0
x3
0
1
Die eindeutige Lösung des LGS ist somit:


0
 1 
−2
11) a)
0
0
x1
0
x2
-1
x1 x2
3 -70 -600
-30 701 6009
70
200
3
1
9
-9
10
9
-1
10
bei exakter Rechnung.
Lsg. :
9
b) Wir runden nun bei jedem Rechenschritt auf ganze Zahlen. Dabei sind
die Werte bei denen die Rundung tatsächlich “greift” durch Anfügen des
Dezimalpunktes gekennzeichnet:
1
0
0
x1
0
x2
x1
3
-30
x2
-70
701
23.
11.
-1
-600
6009
200
9
-1.
-1
-177.
1.
−177.
, die wir bei Rundung auf ganze Zahlen nach jedem ReDie Lsg.
1.
chenschritt erhalten, ist also als Näherung für die ”wirkliche” Lsg. völlig
unbrauchbar.
12)
0
0
0
0
x4
0
0
0
x2
0
0
x1
2
4
2
4
2
2
6
10
-2
0
0
1
0
x2
1
2
1
2
1
1
3
5
-2
2
x3
-2
-4
-2
-4
-2
-2
-6
-10
2
0
0
0
1
x4
0
1
-1
3
0
0
x1 , x3 sind frei wählbar. Die Dimension der Lösungmenge ist also = 2 und
die Lösungsmenge selbst besteht aus allen Linearkombinationen der ermittelten Fundamentallösungen (1, −2, 0, 0)⊤ und (0, 2, 1, 0)⊤ und ist also die
lineare Hülle dieser Fundamentallösungen:

 

 
0 1





 



2
−2
 + t2   t1 , t2 ∈ R
L = t1 
 1 
 0 






0
0
2
Die zweite und dritte Zeile im zweiten Tableau können gestrichen werden,
da sie sich aus der ersten Zeile durch Multiplikation mit 3 bzw. mit 5 ergeben und somit keine neue Information liefern.
Die Dimension der Lösungsmenge ist gleich der Zahl der benötigten Fundamentallösungen und damit = 2.
13)
0
0
0
0
x3
0
0
0
x2
0
0
x4
0
x1
x2
1
1
1
0
2
5
4
3
1
0
-2
1
2
5
9
3
+2
12
15
1.5
0
1
0.5
0 −0.5
2
1
1
0
x3
-3
-1
0
5
x4
-2
-1
-3
-2
-1
1
-3
-7
-1
-8
-10
−0.5
−0.5
−1
-1
1.5
−0.5
3
1
s
2
1
-1
0
1
-1
-1
5
1
4
8
0.8
−2.4 6= 0
0
0
0
0
u
2
1
-1
-3
1
-1
-1
2
1
4
5
0.5
0
0
-1
0
-1
Die Zahlenwerte, die festgelegt sind, sind wieder durch unterstreichen gekennzeichnet. Die übrigen Zahlenwerte werden über die Kellerzeilen berechnet.
Für das homogene LGS setzen wir s = u = 0 und erhalten die in der
ersten Auswertungszeile ermittelte Fundamentallösung (1, 0.5, −0.5, 1.5)⊤
und damit die Lösungsmenge:


 1






 0.5


t
∈
R
t
L= 
−0.5  





1.5
Zusatzbemerkung: Statt die frei wählbare Koordinate x1 = 1 zu setzen,
können wir sie auch = 2 setzen, was in der dritten Auswertungszeile geschieht. Wir erhalten so die Fundamentallösung (2, 1, 1, 3)⊤, die nur ganze
3
Zahlen enthält und damit die Lösungsmenge:


 2







1
 t t ∈ R .
L= 
 −1  





3
a) Hier ist s := −1 und u := 0 zu setzen und damit führt das letzte Tableau
zum Widerspruch. Das LGS ist also nicht lösbar.
b) Hier ist s := 0 und u := −1 zu setzen und damit führt das letzte
Tableau nicht zum Widerspruch. Das LGS ist also lösbar, aber nicht eindeutig. Da wir eine Fundamentallösung des zugehörigen homogenen LGS
schon bestimmt haben, brauchen wir nur noch eine spezielle Lösung des inhomogenen LGS zu finden, indem wir s := 0, u := −1 und die frei wählbare
Koordinate x1 := 0 setzen. Wir erhalten so über die zweite Auswertungszeile (0, −0.5, −0.5, −0.5)⊤ als eine spezielle Lösung und damit


  
1
0






  0.5  −0.5




t
∈
R
t
+
L= 
−0.5   −0.5  





1.5
−0.5
als Lösungsmenge.
Zusatzbemerkung: Statt die frei wählbare Koordinate x1 = 0 zu setzen,
können wir sie auch = 1 setzen, was in der vierten Auswertungszeile geschieht. Wir erhalten so die (1, 0, −1, 1)⊤ als eine spezielle Lösung, die nur
ganze Zahlen enthält und damit die Lösungsmenge:


  
2
1






  1  0




t
∈
R
t
+
L= 
−1   −1  





3
1
14) a)
A Halbwertzeit 1h
B Halbwertzeit 2h
C Halbwertzeit 3h
x1,2,3 =?
4
Anfangsmasse
x1 mg
x2 mg
x3 mg
nach 6h : Masse von A
Masse von B
Masse von C
nach 12h : Masse von A
Masse von B
Masse von C
nach 18h : Masse von A
Masse von B
Masse von C
x3
x2
x1
2−6
2−12
2−18
−2−4
−2−12 · 15
−2−18 · 255
−2−6 · 15
+2−18 · 105
x2
2−3
2−6
2−9
−2−1
−2−6
−2−9 · 3
98304
2176
x1
x1
x1
= 6
6/1
2x
2
x
2
2
=
2x6/2 x
23
3
3
= 2
6/3
2x
2x
1
1
=
12/1
2x
2x12
2
2
= 6
12/2
2x
2
x
3
3
=
12/3
4
2x
2x
1
1
=
18/1
2x
2x18
2
2
= 9
18/2
2x
2
x
3
3
=
18/3
6
2
2
-1
x3
2−2
2132
2−4
139
−6
2
24.875
-8528
-394
-108.375
-25216
39.375
-98304
1296
-1
Wir erhalten somit die Anfangsmasse von 98304mg für Komponente A, von
2176mg für Komponente B, von 1296mg für Komponente C.
Wir betrachten nun ein neues Präparat mit einer Halbwertzeit von 2h bei
A und einer Halbwertzeit von 3h bei B und C. Am Anfang haben wir die
gleiche Mengen x1,2,3 für A, B bzw. C wie oben.
Gewicht des Präparats beträgt nach
98304 2176 1296
+ 2 + 2 = 13156
2+3
2
2
98304 2176 1296
+ 4 + 4 = 1753
12h :
26
2
2
98304 2176 1296
18h :
+ 6 + 6 = 246.25
29
2
2
6h :
5
x3
x1
2−3
2−6
2−9
−2−1
2−6
−3 · 2−9
x2
2−2
2−4
2−6
-1
0
0
0
0
0
1
x1
98304
0
x3
2−2
2−4
2−6
3472
-1
s
13156
1753
246.25
-52624
-1536
-576
-98304
0
-1
0
LGS nicht eindeutig lösbar; Rekonstruktion nicht möglich.
Dies kann man auch ohne Lösung des LGS sofort erkennen; denn die Koeffizientenmatrix hat den Rang ≤ 2, da zwei Spalten gleich und damit erst
recht l.a. sind.
14) b)
x1 (g) Äpfel
x2 (g) Bananen
x3 (g) Orangen
x1,2,3 =?
x1 · 0.3 + x2 · 1.1 + x3 · 1.0 !
= 9
Eiweiß :
100
x1 · 0.6 + x2 · 0.2 + x3 · 0.2 !
Fett :
= 5
100
x1 · 15 + x2 · 22 + x3 · 12 !
Kohlehydrate :
= 194
100
x1
x2
x3
-1
0
0.3
1.1
1.0
900
0
0.6
0.2
0.2
500
0
15
22
12
19400
x3 -0.3
-1.1
-900
0 0.54 -0.02
320
0 11.4
8.8
8600
x2
27
16000
0
249
149400
x1
-600
600
200
500
-1
Somit brauchen wir 600g Äpfel, 200g Bananen und 500g Orangen.
6