ferienkurs experimentalphysik 4 - TUM

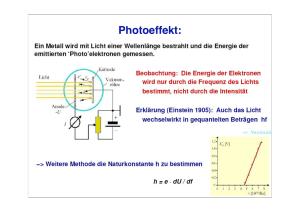
F ERIENKURS E XPERIMENTALPHYSIK 4
Vorlesung 1
Einführung in die Quantenmechanik
Felix Bischoff, Christoph Kastl, Max v. Vopelius
24.08.2009
Vorbemerkung
Dieses Skript ist Teil des Ferienkurses Experimental Physik IV im Sommersemester
2009 und im Rahmen von diesem erstellt worden. Es basiert auf der Vorlesungsmitschrift von Prof. Kruecken (SS09) [1], dem Experimental Physik IV Skript von Prof.
Gross (SS03) [2], der Vorlesungsmitschrift aus Theoretical Physics II von Prof. Vogl
(WS07/08) [3] und dem Skript zum Ferienkurs im SS08 [4]. Wir erheben keinen Anspruch auf Vollständigkeit, vielmehr sollen nur die wichtigsten Sachverhalte mit Hinblick auf bevorstehende Prüfungen nochmals wiederholt werden. Für weitere Vertiefung empfehlen wir die angegebenen Quellen und verweisen auf die darin empfohlene Literatur.
1 Einführung in die Quantenphysik
Situation in der Physik Anfang des 20. Jahrhunderts:
• Teilchenbild in der klassischen Mechanik: jedem Teilchen kann bei bekannten
Anfangsbedingungen eine eindeutige Teilchenbahn zugeordnet werden, d.h.
Ort und Impuls sind wohldefiniert
• Wellenbild in der klassischen Wellentheorie: elektromagnetische Wellen sind
durch die Maxwell Gleichungen vollständig beschrieben und können mit der
ebenen Welle
E(r, t) = E0 · exp [i (k · r − ωt + φ)] mit Amplitude E0 , Wellenvektor k, Kreisfrequenz ω und Phasenkonstante φ gelöst werden
• Mit klassische Theorien lassen sich zu dieser Zeit experimentelle Ergebnisse
vorhersagen und bekannte Phänomene erklären, scheitern jedoch an neuen experimentellen Befunden der Hohlraumstrahlung, des Compton Effekst, des Photoeffekts, des Frank-Hertz-Versuchs und der Elektronenbeugung.
• Diskrepanz zwischen Theorie und Experiment führte zur Entwicklung neuer Hypothesen und schließlich zu neuen Theorien wie der Quantenmechanik
(QM)
2 Welle-Teilchen Dualismus
Jedes physikalische Objekt (Photon, Elektron, Helium Kerne, Fußball) zeigt sowohl
Teilchen- als auch Wellencharakter. Unterschiedliche physikalischen Eigenschaften
müssen mit unterschiedlichen Modellen erklärt werden, wobei allerdings die gleichzeitige Anwendung beider Modelle zu Widersprüchen führt. Diese Problematik heißt
Komplementarität. Es kann nicht entschieden werden, ob ein Teilchen oder eine Welle
1
vorliegt. Im Folgenden wird die Komplementarität von klassischen Wellen und klassischen Teilchen mit Beispielen aus den oben erwähnten, klassisch widersprüchlichen
Phänomenen gezeigt.
2.1 Photoeffekt: Dualismus des Lichtes
Es wurde beobachtet, dass Elektronen durch Bestrahlen mit elektromagnetischen Wellen aus Materie herausgelöst werden können. Der Effekt an sich war klassisch leicht
erklärbar und man erwartete ein kontinuierliches Energiespektrum der ausglösten
Photoelektronen proportional zur eingestrahlten Intensität. Stattdessen wurde eine
diskrete Energiequantelung der Photoelektronen in Abhängigkeit von ihrer Frequenz
(Ee− = h̄ω − EB ) beobachtet und dass der Photoeffekt unabhängig von der Intensität
der Strahlung nur oberhalb einer Grenzfrequenz auftritt.
Auf Grundlage des Plank’schen Strahlungsgesetzes, das die Strahlungsverteilung
von Hohlraumstrahlung beschreibt, entwickelte Einstein die Quantenhypothese und
ordnete elektromagnetischer Strahlung einen Teilchencharakter zu. Er postulierte,
dass die Energie von Licht durch Photonen gequantelt mitgeführt wird und mit der
Frequenz verknüpft ist: E = hν = h̄ω. Ein Photon kann in einem Einzelprozess also
maximal die Energie E = h̄ω auf ein Elektron übertragen, die größer oder gleich der
Austrittsarbeit EB des Elektrons aus der Materie sein muss, um ein Photoelektron mit
Energie Ee− = h̄ω − EB zu erzeugen. Einstein erhielt fuer seine Quantenhypothese
1921 den Nobel Preis.
Zusammen mit der Beziehung E = mc2 lässt sich einem Photon die relativistische
Masse m = h̄ω/c2 und damit einen Impuls
p = mv =
h̄ω
2π
ĉ = h̄ ĉ = h̄k
c
λ
zuordnen, der den dualen Charakter von Licht beschreibt und andere Phänomene
wie z.B. den Comptoneffekt erklärt.
2.2 Elektronenbeugung: Dualismus der Materie
Die Verknüpfung p = h̄k zwischen dem Teilchen- und Wellencharakter von Photonen wurde dann von de Broglie allgemein auf mikroskopische Teilchen der Masse m
übertragen, denen er die Wellenlänge
λ=
h
h
h
=
=√
p
mv
2mEkin
2
zuordnete (de Broglie Wellenlänge). Experimentell wurde diese Materiewellenhypothese durch die Beugung von Elektronen an Kristalloberflächen und dünnen Metallfolien und durch Elektronenbeugung an einem Doppelspalt belegt. Wird zum Beispiel
bei Beugung an einem MgO Einkristall für Licht und Elektronen das Produkt aus Monitorabstand und Wellenlänge r0 λgleich eingestellt, werden gleiche Beugungsmuster
beobachtet. Dieser direkte Vergleich demonstriert sehr überzeugend den Wellencharakter von mikroskopischen Teilchen.
Jedem Teilchen mit Ruhemasse m0 6= 0 und Impuls p = mv T kann also durch eine
Materiewelle mit Wellenlänge λ, Kreisfrequenz ω und Phasengeschwindigkeit v ph
beschrieben werden, wobei
h
p
E
ω =
h̄
c2
v ph =
vT
λ =
2.3 Heisenberg’sche Unschärferelation
Man kann ein Teilchen als Wellenpaket durch die Überlagerung unendlich vieler Wellen mit gaußförmiger Amplitudenverteilung beschreiben. Die volle (räumliche) Breite des Maximums ∆x eines solchen normierten Wellenpakets zum Zeitpunkt t = 0
und die volle Breite ∆k der zugehörigen Amplitudenverteilung haben folgende Beziehung:
∆x∆k ≥ 1
Wobei der kleinste Wert ∆x∆k = 1 für eine gaußförmige Amplitudenverteilung eintritt und alle anderen Verteilungen größere Werte liefern. Mit p = h̄k folgt die Heisenberg’sche Unschärferelation
∆x∆p ≥ h̄
Die Konsequenz der (Orts-Impuls-)Unschärferelation ist, dass der Ort und der Impuls eines Teilchens nicht beliebig genau bestimmbar, sondern immer mit einer Unschärfe behaftet sind. Diese Unschärfe ist dabei kein systematischer Fehler der Messung sondern prinzipieller Natur. Man bezeichnet die Messgrößen, deren Genauigkeit durch die Heisenberg’sche Unschärferelation bestimmt ist als komplementär. Weitere komplementäre Größen sind beispielsweise Energie und Zeit:
∆E∆t ≥ h̄
Zur Veranschaulichung der Unschärferelation betrachten wir das Doppelspaltexperiment mit einem einzelnen Elektron. Ein von einer Quelle ausgesandtes Elektron trifft
3
auf einen Doppelspalt, interferiert mit sich selbst und erzeugt einen Punkt irgendwo
auf einem Monitor. Bei genügend häufiger Wiederholung erscheint ein Interferenzmuster auf dem Bildschirm. Möchte man z.B. mit einem Detektor bestimmen durch
welchen Spalt das Elektron geflogen ist, d.h. ∆x → 0, wird die Impulsunschärfe so
groß, dass die Ungenauigkeit des Elektrons auf dem Schirm größer ist als die Entfernung zweier benachbarter Maxima und es somit zu keinem Interferenzmuster kommen kann (Beweis siehe Übung). Die Messung beeinflusst also die Eigenschaften des
Elektrons.
Das Doppelspaltexperiment lässt sich verallgemeinern. Das genaue Verhalten eines
einzelnen Teilchens in einem Experiment kann nicht deterministisch vorhergesagt
werden. Man kann allerdings eine Wahrscheinlichkeit für ein Ergebnis angeben und
durch genügend häufige Wiederholung verifizieren. Für mikroskopische Systeme geht
die deterministische Beschreibung (genaue Zustände) in eine statistische Beschreibung (Zustandswahrscheinlichkeiten) über.
3 Fundamental Begriffe der Quantenmechanik
Die mathematische Beschreibung eines klassischen Teilchens mit Wellencharakter,
die physikalisch sinnvoll ist, stellt sich als kompliziert heraus. Die naive Zuordnung
einer einzelnen Materiewelle zu einem Teilchen ist unzureichend (z.B. Ausbreitung
im gesamten Raum vs. lokalisiertes Teilchen) , wie auch die Assoziation eines Teilchens mit einem Wellenpaket. Obwohl das Wellenpaket den richtigen Ansatz zeigt
und man daraus wichtige Ergebnisse wie die Heisenberg’sche Unschärferelation ableiten kann, beinhaltet es immer noch physikalisch nicht sinnvolle Aussagen. So dispergiert ein Wellenpaket beispielsweise, obwohl sich die Form eines klassischen Teilchens nicht verändert und es ist mit einem Strahlteiler teilbar, ein klassisches Teilchen
wie ein Elektron allerdings nicht. Um die Welleneigenschaften eines klassischen Teilchens physikalisch korrekt beschreiben zu können wurde die Quantenmechanik entwickelt. In dieser Vorlesung wird im Wesentlichen ein nicht-relativistischer Teil der
Quantenmechanik vorgestellt: die Wellenmechanik mit Schrödinger-Darstellung.
3.1 Zustand
Der Zustand eines mikroskopischen Systems in der Quantenmechanik wird als Ψ
oder in der bra-ket-Notation als |Ψi bezeichnet und ist ein Element des abstrakten
Hilbertraums. Für den Gebrauch im Rahmen dieses Repetitoriums wird allerdings
hauptsächlich die Projektion des Zustandes in den Ortsraum Ψ(r, t) (auch bekannt
als Zustands- oder Wellengleichung) verwendet. Um die räumliche und zeitliche Entwicklung einer Zustandsgleichung beschreiben zu können, wird eine Differentialglei-
4
chung benötigt (Schrödingergleichung) und um die Zustände durch messbare Eigenschaften (Observablen) charakterisieren zu können werden Operatoren benötigt.
3.2 Wahrscheinlichkeitsinterpretation
Die Heisenberg’sche Unschärferelation und das Doppelspatlexperiment zeigen, dass
keine deterministischen Aussagen über quantenmechanische Objekte mehr gemacht
werden können. Statt dessen werden nur Wahrscheinlichkeitsaussagen gemacht, wobei die Zustandsfunktion Ψ nach Born als Wahrscheinlichkeitsdichteamplitude aufzufassen ist und sich somit die Wahrscheinlichkeit W (r, t)dV ein Objekt zum Zeitpunkt t
im Volumen dV zu finden aus der Wahrscheinlichkeitsdichte |Ψ(r, t)|2 berechnet.
W (r, t)dV = Ψ∗ ΨdV = |Ψ|2 dV
Dabei muss die Normierungsbedingung
Z +∞
−∞
|Ψ|2 dV = 1
erfüllt sein muss, da sich das Teilchen rigendwo im Raum befinden muss.
3.3 Die Schrödingergleichung
Die Schrödingergleichung (SE) ist die Grundgleichung der nicht-relativistischen Quantenmechanik, die die Entwicklung einer Zustandsfunktion Ψ(r, t):
i
Ψ(r, t) = Ψ0 ei(kr−ωt = Ψ0 e h̄ (pr−Et)
beschreibt. Aus Analogieüberlegungen zur Wellenoptik heraus postulierte Schrödinger die Gleichung
!
∂
h̄2 2
ih̄ Ψ(r, t) = −
∇ + E pot (r, t) Ψ(r, t)
∂t
2m
Dies ist die zeitabhängige Schrödingergleichung für den allgemeinen Fall E(t) = Ekin (t) +
E pot (t) und p = p(t). Im stationären Fall E = const lässt sich über den Separationsansatz
Ψ(r, t) = Ψ(r, 0) · e−iωt
5
die stationäre Schrödingergleichung
−h̄2 2
∇ + E pot
2m
!
Ψ(r) = EΨ(r)
herleiten.
3.3.1 Eigenschaften der Schrödingergleichung
• relativistisch nicht invariant
• lineare, homogene DGL ⇒ Lösungen Ψ1 , Ψ2 können linear zu Lösung Ψ3 überlagert werden (Superposition): Ψ3 = aΨ1 + bΨ2
• Eigenwertgleichung für die Zustandsfunktion Ψ
3.4 Observable und Operator
Die klassische Messgröße wird durch die Observable ersetzt und jeder dieser physikalischen Größen ein Operator zugeordnet, der sie mit der Zustandsfunktion verknüpft.
Aufgrund der Wahrscheinlichkeitsinterpretation sind nur Erwartungswerte von Observablen zugänglich. Für den Erwartungswert h Ai einer Observable A gilt:
h Ai =
Z +∞
−∞
Ψ∗ ÂΨdV
Dabei ist  der der Observablen zugeordnete Operator, der eine bestimmt mathematische Operation an der Zustandsfunktion ausübt. Im Ortsraum gelten folgende
Zuordnungen:
r → r̂
E pot → V (r)
Ekin → Êkin = −
h̄2 2
∇
2m
h̄2 2
∇ + V (r)
2m
p → p̂ = −ih̄∇
E → Ĥ = −
L → L̂ = −ih̄(r × ∇)
6
3.4.1 Eigenwert und Eigenfunktion
Wendet man einen Operator  auf eine Zustandsfunktion Ψ an und dieser reproduziert Ψ lediglich bis auf einen konstanten Faktor a, so heißt Ψ Eigenfunktion und der
Erwartungswert h Ai heißt Eigenwert:
ÂΨ = ZaΨ
Z
Z
∗
∗
h Ai =
Ψ ÂΨdV = Ψ aΨdV = a Ψ∗ ΨdV = a
Dabei ist a das messbare Ergebnis der Observale A (d.h. A = a), deren mittlere quadratische Schwankung (h∆A2 i) gleich null ist (d.h. A ist zeitlich konstant; man misst
immer den gleichen Wert). Für die Standardabweichung ∆A gilt:
q
∆A = h A2 i − h Ai2
Alle Operatoren sind hermitesch, d.h. ihre Eigenwerte sind reell, da sie eine physikalisch messbare Größe darstellen.
3.5 Anmerkung zur Schrödingergleichung
Die SG ist das mathematische Werkzeug um quantenmechanische Probleme zu lösen. Physikalisch sinnvolle Lösungen ergeben sich dabei aus der Normierung der Zustandsfunktion und physikalisch begründeten Neben- und Randbedingungen. Wichtig ist dabei auch die Transformation der SG, d.h. in erster Linie des ∇-Operators,
in dem Problem entsprechende Koordinaten und die Wahl des Ansatzes für die Zustandsfunktion. Für entsprechende Standardbeispiele zu speziellen Lösungen der SG
(Potentialtstufe, -wall, -topf, Harmonischer Oszillator, Kugelsymmetrisches Potential) sollte unbedingt ein Blick in die Vorlesungsskripte oder in ein Buch geworfen werden. Einige Beispiele und Anwendungen werden auch in der Übung gegeben, bzw.
in folgenden Vorlesungen (z.B. Ein-Elektronensystem).
4 Spin
Stern und Gerlach beobachteten, dass sich ein Strahl aus Silberatomen (Silber enthält genau ein ungepaartes Elektron) beim Durchlaufen eines inhomogenen magnetischen Feldes in zwei Teilstrahlen aufspaltet. Daraus schlossen sie, dass Elektronen
außer ihrer Ruhemasse m0 und der Ladung −e noch eine weiter Eigenschaft besitzen müssen, durch die die Elektronen mit einem magnetischen Feld wechselwirken.
Diese Eigenschaft ist der Eigendrehimpuls der Elektronen: der Elektronenspin S. Der
Elektronenspin (bzw. dessen z− Komponente) kann zwei Einstellungen haben: ± 12 .
7
Aus der Definition des Betrages und der z−Komponente ergeben sich die zwei Quantenzahlen s und ms .
4.1 Fermionen und Bosonen
Ähnlich dem Elektronenspin lässt sich allen Quantenteilchen eine Drehimpuls- Eigenschaft, also ein Spin, zuordnen. Diese Quanteneigenschaft, die zur Drehimpulserhaltung notwendig ist und sich wie ein Drehimpuls transformiert, hat allerdings
kein klassisches Analogon. Alle Teilchen lassen sich dadurch in zwei Arten aufteilen: Fermionen und Bosonen. Fermionen haben einen halbzahligen Spin und eine antisymmetrischen Austauschsymmetrie (alle realen Elementarteilchen wie z.B. Elektronen, Protonen, Neutronen, Quarks, Neutrinos) und Bosonen besitzen einen ganzzahligen Spin (z.B. Photonen, Phononen) und eine symmetrische Austauschsymmetrie.
Wichtige Folgen des Spins sind unterschiedliche Intensitäten bei Streuexperimenten
und das Pauli-Verbot für Fermionen. Das Pauli Verbot besagt, dass zwei Fermionen
mit identischem Satz an Quantenzahlen nicht gleichzeitig in einem System existieren
können.
Literatur
[1] http://av.ph.tum.de/
[2] http://www.wmi.badw.de/teaching/Lecturenotes/index.html
[3] Online nicht mehr verfügbar
[4] http://www.physik.tu-muenchen.de/studium/betrieb/ferienkurse/2008s/exphys4/inde
8