Grundlegende Begriffe: Funktionen

2
Grundlegende Begriffe:
Funktionen
Hohe Gedanken brauchen eine hohe Sprache
Aristophanes
In diesem Kapitel werden wichtige Eigenschaften von Funktionen besprochen. Dazu werden zunächst die grundlegenden mathematischen Begriffe
zusammengefaßt. In der funktionalen Programmierung sind definierende
Gleichungen von Funktionen das A und O. Definitionen sind funktionale
Programme.
Abstraktion ist ein fundamentales Prinzip der Informatik. Eine Funktion
kann als Abstraktion eines Ausdrucks aufgefaßt werden. Wie das technisch
aussieht, wird ebenfalls in diesem Kapitel diskutiert.
Die Lernziele im Einzelnen:
• Den mathematischen Funktionsbegriff verstehen
• Unterschied zwischen partiellen und totalen Funktionen
• Definierende Gleichungen
• Funktionen als Abstraktion von Ausdrücken
• Funktionen als Argumente von Funktionen
• Klammerfreie Schreibweise von Funktionen nach Curry
• Fallunterscheidung zur Funktionsdefinition
Vers. 7.11.98
6
Funktionen
2.1 Funktionen
Funktionen sind aus der Mathematik bekannt. Mit Funktionen kann man nicht
nur rechnen sondern auch Algorithmen formulieren. Davon handelt diese Vorlesung. Die Begriffsbildungen in Mathematik und Informatik sind völlig gleichartig. Allerdings interessiert man sich im allgemeinen in der Mathematik für die
Eigenschaften einer Funktion (z.B. Stetigkeit, Differenzierbarkeit), in der Informatik dagegen konkret für die Berechnung von Funktionswerten.
Eine der einfachsten denkbaren Funktionen ist die Identität:
> id’ x = x
?: id’ hello world
„hello world“
Diese Funktion1 liefert ihr Argument x als Funktionswert. Etwas anspruchvoller
ist die Funktion:
> quadrat x = x*x
?: quadrat 4
16
Die Definition von quadrat stützt sich auf die primitive Funktion * ab2.
Konstanten sind 0-stellige Funktionen:
> seite = 5
> flaeche = quadrat seite
?: flaeche
25
Wir klären zunächst einige Begriffe:
DEF.:
Eine Funktion f ist eine rechtseindeutige Relation f ⊆ A × W über der
Argumentmenge A und der Wertemenge W,
d.h: (a,w), (a,w’) ∈ f ⇒ w = w’.
1. Folgende Konventionen gelten in diesem Text:
> steht am Beginn einer Zeile, die eine Definitionsgleichung oder Teil davon enthält.
?: steht am Beginn einer Zeile, die Eingabe für das Haskell-System ist. In der / den Folgezeile(n) steht das Ergebniss.
2. Operatoren wie +, * usw. können als Funktionen aufgefaßt werden. Dazu später mehr.
Vers. 0.2 / 10-98
7
Grundlegende Begriffe: Funktionen
Für (a,w) ∈ f schreibt man: f(a) = w oder (f a) = w oder f a == w . In Definitionen und allgemeinen Erörterungen verwenden wir die mathematische
Schreibweise f(a) , in HASKELL-Programmen die klammerfreie Schreibweise f a.
Die Vorteile werden später klar, anfangs ist sie etwas gewöhnungsbedürftig.
Statt Argument- bzw. Wertemenge sagt man oft Argumentbereich und Wertebereich.
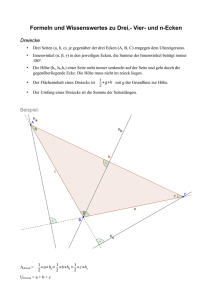
ABBILDUNG 1.
Funktion dargestellt als Relation
Einem Argument
werden nie
zwei verschiedene
Werte zugeordnet
A
W
Die in Abb. 1. dargestellte Funktion f ist so zu verstehen: Die Pfeile verlaufen
vom Argumentbereich zum Wertebereich. Ein Argument x besitzt den Wert w ,
auf den der Pfeil zeigt, der bei x beginnt. f besitzt einige typische Eigenschaften:
• Die Elemente des Argumentbereichs sind gleichartig. Man sagt: sie haben
den gleichen Typ .
• Gleiches gilt für den Wertebereich, dessen Typ sich von dem des Argumentbereichs — wie im Beispiel — unterscheiden kann, nicht muß.
• Die Anzahl der Elemente von Argument- und Wertbereich ist unterschiedlich. Auch das kann, muß nicht so sein. A oder W können auch unendlich
sein.
• Es gibt einen Wert v, der mehrere Urbilder a, a’ hat, d.h.
f(a) = f(a’) = v . Deshalb ist die dargestellte Funktion nicht injektiv .
• Nicht alle Elemente des Wertebereichs treten als Wert eines Arguments auf.
Die Funktion ist nicht surjektiv.
8
Funktionen
• Nicht jedes Argument besitzt einen Funktionswert. Die Funktion ist partiell .
Die Menge der Argumente, auf der eine Funktion definiert ist, heißt Definitionsbereich von f .
Partielle Funktionen
sind gefährlich!
Partielle Funktionen machen dem Programmierer das Leben schwer: vor einer
Funktionsapplikation f(a) muß nämlich geprüft werden, ob f für a überhaupt
definiert ist. Sonst kann die Ausführung des Programms zur Katastrophe führen.
Das beliebteste Beispiel ist die Division durch 0. Die (ganzahlige) Division kann
man offenbar als Funktion div : Int × Int→ Int auffassen. div ist eine zweistellige Funktion. Der Argumentbereich besteht aus Paaren von ganzen Zahlen
— Divident und Divisor —, der Wertebereich ebenfalls aus ganzen Zahlen,
deren Typ hier mit Int bezeichnet wird. Ob div (4711 , (a - b) ) wohldefiniert ist,
hängt davon ab, ob a ≠ b . Die Division ist nämlich partiell. Bekanntlich ist sie
auf der Menge {(x,0) | x aus Int } undefiniert.
Die einführten Begriffe werden zusammengefaßt in:
DEF.:
Eine Funktion f : A → W heißt
•injektiv, wenn a,a’ ∈ A : a ≠ a’ ⇒ f(a) ≠ f(a’)
•surjektiv, wenn ∀ w ∈ W ∃ a ∈ A : f(a) = w
•bijektiv, wenn f injektiv und surjektiv ist
•total, wenn ∀ a ∈ A : ∃ w ∈ W : f(a) = w
•partiell, wenn sie nicht total ist.
•Der Definitionsbereich von f ist die Teilmenge A’ ⊆ A , auf deren Elementen f definiert ist. Wenn A’ ⊂ A , dann ist f partiell.
•Eine Funktionen von n Elementen f : A → W,
A = A1 ×… × An , heißt n-stellig.
Unter der Komposition von Funktionen
f : A → W und g : W→ V
versteht man die Funktion
h = g . f , h : A → V mit
h(a) = g( f(a) ).
Injektive Funktionen f besitzen eine Umkehrfunktion f -1. Für alle Argumente x,
für die f definiert ist, gilt:
f -1 ( f(x)) = x oder f -1. f = id
Vers. 0.2 / 10-98
9
Grundlegende Begriffe: Funktionen
2.2 Funktionsdefinition,Variablen, Parameter
Funktionen werden durch Gleichungen definiert. Diese bilden die Grundlage der
Berechnung von Funktionswerten. Kommt auf der rechten Seite der definierenden Gleichung einer Funktion f eine Funktion g vor, sagen wir: f stützt sich auf
g ab, z.B f(x) = g(x) + k .
Um den Wert f(a) zu berechnen, muß der Wert g(a) berechnet und um k
erhöht werden. Funktionen, die im Rahmen der Programmiersprache nicht definiert zu werden brauchen, heißen primitive Funktionen. Dazu gehören insbesondere die arithmetischen Funktionen. Primitive Funktionen sind im allgemeinen
keine Bibliotheksfunktionen. Jedes Programmiersystem kennt Programmbibliotheken, in funktionalen Programmiersprachen auch Funktionsbibliotheken
genannt. Sie enthalten nützliche, häufig verwendete Programme (Funktionen), so
daß nicht jeder Programmierer das Rad neu erfinden muß.
Beispiele: quadrat stützt sich auf die primitive Funktion (hier besser Operation) * ab. Die Funktion
> quaderVol h = flaeche * h
Definierende
Gleichungen sind
das A und O der
funktionalen
Programmierung
stützt sich auf die oben definierte Funktion flaeche und die primitive Funktion
* ab. Sie berechnet das Volumen eines Quaders der Grundfläche flaeche mit
der Kantenlänge seite und der Höhe h. Die nicht sonderlich interessante
Funktion:
> id’’ x = sqrt (quadrat x)
stützt sich auf die Bibliotheksfunktion sqrt sowie auf quadrat ab.
Die Klammerung von quadrat x ist wichtig, sonst würde sqrt auf die Funktion quadrat angewendet und nicht auf den Wert, der sich bei Berechnung von
quadrat x ergibt.
Hinter dieser Feststellung stecken mehrere wichtige Fragen: Wie wird ein Funktionswert eigentlich berechnet? In welcher Reihenfolge werden Teile einer Definition berechnet? Wie wird der Versuch der Berechnung von Funktionswerten
für nicht erlaubte Argumente von z.B. von quadrat ’’Hello World’’ verhindert? Dazu später.
Funktionsdefinitionen sind strikt von der Berechnung von Funktionswerten zu
unterscheiden. Ist f eine bereits definierte Funktion und a ein Wert aus dem
Definitionsbereich der Funktion, so ist f a ein Funktionswert aus dem Wertebereich von f . Werte werden berechnet, wenn f aufgerufen wird, sei es interaktiv
10
Funktionsdefinition,Variablen, Parameter
vom Benutzer, sei es im Zuge der Berechnung einer Funktion h, auf die sich die
Definition von h abstützt. f a nennt man auch eine Funktionsapplikation.
Wir wollen einen ersten Eindruck davon vermitteln, wie die Berechnung von
Funktionswerten stattfindet. Der Ausdruck
Berechnung von
Ausdrücken
erfolgt durch
Reducktion
quaderVol 10
soll berechnet werden. Dazu wird die Definition von quaderVol eingesetzt.
Alle Vorkommen des formalen Parameters h müssen durch den aktuellen Parameter 10 ersetzt werden. Wir erhalten
flaeche * 10
Im nächsten Schritt wird flaeche durch seine Definition (s.o.:
flaeche = quadrat seite) ersetzt. Das Ergebnis ist:
quadrat seite 10
Unter Verwendung der Definitionen von seite bzw quadrat erhält man in den
folgenden Schritten:
seite * seite * 10
seite * 5 * 10
seite * 50
5 * 50
250
Einen Ersetzungsschritt nennt man Reduktion. Beachte, daß die Folge der
Reduktionsschritte nichtdeterministisch sein kann. Im Beispiel hätte z.B. seite
vor quadrat reduziert werden können. Ein reduzierbarer (Teil-)Ausdruck heißt
Redex (reducible expression). Das Verfahren ist nichtdeterministisch, wenn
irgendwann im Verlauf der Reduktion mehr als eine Redex im zu reduzierenden
Ausdruck vorkommt. Das Reduktions- oder Berechnungsverfahren endet, wenn
es keinen Redex mehr gibt. Entweder ist dann bereits der Funktionswert berechnet oder der Ausdruck enthält nur noch primitive Funktionen, die systemintern
ausgewertet werden. Dazu gehört die Multiplikation * . Ein nicht mehr reduzierbarer Ausdruck wird Normalform genannt.
Es schließen sich mehrere Fragen an: terminiert die Folge von Reduktionen
immer? Angenommen, man könnte quadrat x durch x*x und umgekehrt ersetzen. Dann gäbe es offensichtlich eine nichtterminierende Folge von Reduktionen. Liefern verschiedene Reduktionsfolgen dieselbe Normalform? Sind
Vers. 0.2 / 10-98
11
Grundlegende Begriffe: Funktionen
primitive Funktionen unverzichtbar oder dienen sie nur einer effizienteren Ausführung? Wir werden den Fragen später nachgehen.
In Definitionen:
formale Parameter
In Ausdrücken:
Argumente oder
aktuelle Parameter
Variablen sind in
funktionalen
Sprachen nicht
veränderlich!
Folgende Sprechweise hat sich in der Informatik eingebürgert: die im Zuge der
Definition einer Funktion verwendeten Variablen werden oft (formale) Parameter genannt, die Werte, für die ein Funktionswert berechnet werden soll, heißen
Argumente, oder aktuelle Parameter.
Die Bezeichung Variable ist eigentlich unpassend. Sie entstammt der Mathematik, wo man gelegentlich von einer unabhängigen Veränderlichen spricht, womit
nichts anderes gemeint ist, als daß für eine Variable x ein beliebiger Wert des
Definitionsbereichs eingesetzt werden kann.
In einem funktionalen Programm ist eine Variable ein Bezeichner für einen Wert.
Im Gegensatz zu imperativen Programmiersprachen1 wie Pascal, Java oder C ist
der Wert, den eine Variable bezeichnet, nicht veränderbar. Als wichtige Konsequenz halten wir fest, daß Funktionen für gleiche Argumentwerte immer das
gleiche Ergebnis liefert — eine in der Mathematik selbstverständliche Eigenschaft, die in imperativen Programmiersprachen nicht erfüllt ist.
2.3 Funktionen als Abstraktion von Ausdrücken
Funktionsapplikationen gehören zur den Ausdrücken oder Formeln (expressions)
der Sprache. Sie besitzen einen Wert, z.B.
?: sqrt (quadrat 5 + quadrat 7)
8.60233
Mit arithmetischen Ausdrücken verhält es sich selbstverständlich genau so:
?: 3+5*(3-7)
-17
ist kein besonders aufregendes Exemplar. Wie die Menge aller Ausdrücke genau
definiert ist — ihre Syntax von Ausdrücken — wird in der Programmiersprache
festgelegt; dazu später mehr.
Wir wollen vielmehr der Frage nachgehen, wie sich Funktionsdefinitionen und
Ausdrücke zueinander verhalten. Ausdrücke werden, wie eben festgestellt, im
1. Später werden die Untersschiede von funktionalen und imperativen Programmiersprachen genauer herausgearbeitet.
12
Funktionen als Abstraktion von Ausdrücken
wesentlichen durch Funktionsapplikation gebildet. Umgekehrt kann eine Funktion auch als Abstraktion eines Ausdrucks aufgefaßt werden kann:
Abstraktion von
Konstanten in
Ausdrücken
liefert Funktionen
> abstr3 x = x+5*(x-7)
ist eine Funktion, die von der Konstanten 3 abstrahiert. Manchmal nennt man das
auch Parametrisierung des Ausdrucks. Nicht überraschend, daß
?: abstr3 3
-17
den gleichen Wert liefert wie der ursprüngliche Ausdruck, in dem der hier als
Argument verwendete Wert 3 ,,fest verdrahtet”1 ist. Durch Abstraktion sind aus
einem Ausdruck unendlich viele entstanden, u.a.
?: abstr3 4711
28231
was dem Ausdruck 4711+5*(4711-7) entspricht.
Die Abstraktion von Ausdrücken zu Funktionen ist so wichtig, daß HASKELL dafür
eine spezielle Notation bereitstellt, die sogenannte λ−Abstraktion. Sie besteht
aus einem Ausdruck, in dem sogenannte freie Variablen vorkommen und Variablenbindungen der Form λ x .
?: \x -> x+5*(x-7)
<<function>>
Auch anonyme
Funktionen
können
nützlich sein
Das liest sich so: \x -> x+5*(x-7) ist die Funktion von x, die als Wert die
Zahl liefert, die sich ergibt, wenn man für x eine Zahl a als Argument einsetzt
und a+5*(a-7)ausrechnet, z.B:
?: (\x -> x+5*(x-7)) 4711
28231
Das Ergebnis überrascht nicht. Der einzige Unterschied zu abstr3 besteht
darin, daß wir im zweiten Fall eine anonyme Funktion verwendet haben. Das ist
manchmal nicht nur praktisch, sondern hat einen tiefliegenden theoretischen
Hintergrund, auf den wir noch ausführlich zu sprechen kommen.
Abstraktion ist ein zentrales Prinzip der Informatik. Es geht im Kern darum,
durch Abschwächen von bestimmten Randbedingungen — im Beispiel das Vorkommen der Konstante 3 in einem auszuwertenden Ausdruck — ein allgemeineres Problem zu lösen, von dem das ursprüngliche ein Spezialfall ist.
1. Informatikjargon für alles, was nicht parametrisiert ist
Vers. 0.2 / 10-98
13
Grundlegende Begriffe: Funktionen
2.4 Funktionen von Funktionen: Curry-Darstellung
Von der ungeklammerten Schreibweise von Funktionsdefinitionen und -applikationen, der Curry-Notation (currying),1 haben wir schon Gebrauch gemacht.
Was hat es damit auf sich? Als erstes ist festzustellen, daß die Definition von
Funktionen (Def 1.1) nahezu beliebige Argument- und Wertebereiche zuläßt.
Argumente können Paare sein — wie im Fall der Division, auch Zeichenketten,
sogar Funktionen. Tatsächlich ist dies der Schlüssel zum Verständnis der CurryNotation von Funktionen. Wir betrachten eine Funktion max’2, die das Maximum von zwei Zahlen berechnet:
> max’ y x = if x > y then x else y
3
Die Funktion max0:
> max0 x = max’ 0 x
hat nur ein Argument. Sie entsteht aus max’ durch Fixieren des ersten Arguments von max’. Das läßt sich auch direkt machen:
?: max’ 0
<<function>>
(max’ 0) ist also eine Funktion, und zwar eine Funktion mit einem Parameter.
Sie bildet das Maximum von 0 und dem aktuellen Parameter:
?: (max’ 0) 23
23
D.h.: die Funktion verhält sich wie max0. Tatsächlich ist es die gleiche Funktion!
max’ angewandt auf sein erstes Argument y liefert eine Funktion, die angewandt auf das zweite Argument x das Maximum von x und y berechnet. Es
besteht aber kein Anlaß, der Funktion einen Namen zu geben. Das wäre lästig,
denn es gibt ziemlich viele davon: max0, max1,.., max4711,..,
maxMinus1,.., für jedes mögliche erste Argument eine. Es reicht also, (max’
x) wie eine anonyme Funktion zu behandeln, gleich wie das konkrete Argument
x aussieht.
Das mag etwas kompliziert erscheinen, hat aber den großen Vorteil der Einheit1. Benannt nach dem Logiker Haskell Curry, gleichzeitig Namenspatron für die Programmiersprache HASKELL. Die nach
Curry benannte Notation wurde zuerst von dem Logiker M. Schönfinkel vorgeschlagen.
2. Bezeichner dürfen das Zeichen ’ enthalten. Wir verwenden die "gestrichene" Schreibweise bessonders, um Namenskollisionen mit in der Standardbibliothek zu vermeiden. max ist so eine Bibliotheksfunktion. Der Versuch, eine eigene Funktion max zu definieren, führt zu einem Fehler.
3. Fallunterscheidungen if .. then .. else werden im nächsten Abschnitt behandelt.
14
Funktionen und Operatoren — Präzedenz und Assoziation
n-stellige Funktionen lassen
sich durch einstellige ausdrücken
lichkeit: es gibt intern nur Funktionen mit einem Argument. Abgesehen vom
praktischen Vorteil, den Einheitlichkeit immer mit sich bringt, gibt es dafür eine
wichtige theoretische Grundlage, die in Kapitel 5 behandelt wird.
Zur Klarstellung: Funktionsdefinitionen (des Programmierers) können selbstverständlich wie bisher ein oder mehrere Argumente haben, die klammerfrei
geschrieben werden. Daß es sich tatsächlich im wesentlichen um Funktionen
handelt, die Funktionen auf Funktionen abbilden -- sogenannte Funktionale -spielt nur hinter den Kulissen eine Rolle.
Wir fassen die Erörterung von Funktionen in Curry-Notation zusammen:
Es gilt: Zu jeder n-stelligen Funktion
f : A1 × … × An → W
gibt es eine Folge fc1, ... fcn von einstelligen Funktionen , so daß für alle
(a1,...,an), für die f(a1,...,an) definiert ist, gilt:
fc1(a1) = fc2, fc2(a2) = fc , ...., fcn-1(an-1) = fcn, fcn(an) = f(a1,...an) .
Da auch das Umgekehrte gilt, handelt es sich wirklich nur um zwei verschiedenen Darstellungsformen.
Das alles klingt komplizierter als es ist, da die Funktionen fcn , von denen eben
die Rede war, für den Programmierer (fast) gar nicht sichtbar sind. Allerdings
sind manche Fehlermeldungen des HUGS-Systems ohne ein Verständnis der
Curry-Notation nicht interpretierbar. Dazu in Kürze mehr.
2.5 Funktionen und Operatoren — Präzedenz und
Assoziation
Operatoren können
geklammert wie
Funktionen behandelt werden
(Abschnitt, section)
Operatoren sind Funktionen in anderer Schreibweise: Infix-Operatoren stehen im
allgemeinen zwischen zwei Argumenten — wie das von arithmetischen Ausdrücken bestens bekannt ist. Manchmal ist für Operatoren die Präfix-Schreibweise nützlich. In HUGS setzt man dazu einfach das Operatorsymbol in
Klammern. (+) ist die Funktion, die die Summe ihrer Argumente als Wert liefert. (+) kann jetzt überall stehen, wo ein Funktionssymbol erlaubt ist.
Umgekehrt kann man Operatoren wie Funktionen definieren. Das Operatorsymbol wird, wenn es an der Stelle einer Funktion steht, in Klammern gesetzt.
Vers. 0.2 / 10-98
15
Grundlegende Begriffe: Funktionen
Besonders in Verbindung mit der im vorigen Abschnitt besprochenen Möglichkeit, Funktionen mit mehreren Argumenten teilweise anzuwenden, erweist sich
die Präfixschreibweise als nützlich:
Ist ⊗ ein zweistelliger Operator und a, b gültige Argumente, so heißen (a ⊗ )
und (⊗ b) Abschnitte (sections), die durch
(a ⊗ ) y = a ⊗ y
(⊗ b) x = x ⊗ b
definiert sind.
Naheliegende Beispiele sind die Verdopplung (2*) oder der Test, ob ein Wert
positiv ist: (> 0)
‘ und ´
haben verschiedene
Bedeutung
?: (> 0) (-3 * -3)
True
Eine Ausnahme bildet (-x): ’-’ ist die einstellige numerische Negation, die den
negativen Wert ihres numerischen Arguments x liefert.
Funktionsbezeichner können ihrerseits so syntaktisch verändert werden, daß sie
wie Operatoren einsetzbar sind. Dazu muß der Bezeichner in rückwärts gerichtete einfache Anführungszeichen (backquotes) ‘ gesetzt werden. Operatorschreibweise und die Schreibweise für Funktionsapplikation können gemischt
verwendet werden.
?: max (7*2) ((+) 3 12)
15
Vorrangregeln
helfen Klammern sparen
Ein gutes Beipiel für dei Nützlichkeit der Schreibweise sind boolesche Funktionen: Definiert man eine Funktion implies für die aussagenlogische Implikation und sind a und b aussagenlogische Werte1, dann ist die erste der beiden
“aquivalenten Formulierungen offenbar angemessener:
?: a ‘implies‘ b
True
?: implies a b
True
Wie der Ausdruck a*a + 2*a*b + b*b zu berechnen ist, ist jedem geläufig,
wenn a und b wohldefiniert sind: ,,Punktrechnung geht vor Strichrechnung”.
Solche Vorrangregeln (Prioritäts-, Präzedenzregeln) von Operatoren helfen
Klammern sparen. Operatoren höherer Priorität werden vor denen niedrigerer
1. Wie man boolsche Werte ausdrückt, behandeln wir im nächsten Abschnitt.
16
Funktionen und Operatoren — Präzedenz und Assoziation
Priorität angewendet — es sei denn, man setzt Klammern. Das kann zum Beispiel bei Operatoren gleicher Priorität zwingend sein. Vorrangregeln sind
Bestandteil der Sprachdefinition — und wenn man sie ignoriert, nicht selten
Anlaß zu großer Verwirrung. Der folgende Versuch, die Funktion max’ anzuwenden, endet mit einer vorerst noch kryptischen Fehlermeldung:
?: max’ 3 * 4 7
ERROR: a -> b -> b is not an instance of class „Num“
Die Ursache ist im Gegensatz zur Fehlermeldung einfach erklärt: Die Funktionsapplikation besitzt höhere Priorität als alle Operatoren. Im vorliegenden Fall
scheitert die Applikation, weil max’ auf das vermeintlich erste Argument 3 und
danach die entstandene Funktion (Currying!) (max 3) auf * angewendet wird.
* ist keine gültige Zahl, also scheitert die Berechnung. Wegen der dominierenden Priorität der Funktionsapplikation sind hier Klammern zwingend:
?: max’ (3 * 4) 7
12
Klammern besitzen Vorrang vor Applikationen und diese vor Operatoren. Dies
ist in HASKELL so festgelegt. Die Priorität der Operatoren selbst kann dagegen
festgelegt werden. Das ist für selbstdefinierte Operatoren sinnvoll, weil man
Klammern spart.
Eine weitere verbreitete Konvention, die Klammern sparen hilft, ergibt sich aus
der Assoziativität eines Operators. Ob a+b+c als (a+b)+c oder als a+(b+c)
ausgewertet wird, ist bekanntlich gleichgültig, denn + ist rechts- und linksassoziativ. Anders verhält es sich mit der Division:
a / (b / c) ≠ (a / b) / c
In der Mathematik hat man die erste der beiden Klammerungen als verbindlich
festgelegt: Die Division assoziiert rechts. Damit sind die Klammern entbehrlich.
assoziativ =
linksassoziativ
und
rechtsassoziativ
DEF.:
EIN OPERATOR ⊗
heißt rechtsassoziativ, wenn gilt : für alle xi
x1 ⊗ x2 ⊗... ⊗ xn = x1 ⊗ (x2 ⊗...( xn-1 ⊗ xn )...))
Ein Operator ist linksassoziativ wenn gilt:
x1 ⊗ x2 ⊗... ⊗ xn = ((...(x1 ⊗ x2 ) ⊗... xn-1 ) ⊗ xn
Ein links- und rechtsassoziativer Operator heißt assoziativ. Er erfüllt das Assoziativgesetz:
x1 ⊗ ( x2 ⊗ x3 )= ( x1 ⊗ x2 ) ⊗ x3
Vers. 0.2 / 10-98
17
Grundlegende Begriffe: Funktionen
Nicht für jeden Operator ist eine Festlegung zwingend erforderlich, allerdings
muß man in diesem Fall explizit Klammern setzen.
2.6 Funktionen höherer Ordnung
Funktionen, die Funktionen als Parameter besitzen oder deren Wertebereich
Funktionen enthält, nennt man Funktionen höherer Ordnung. Nach den Ausführungen zur Curry-Darstellung ist das eigentlich nichts besonders. Hier geht es
aber nicht um implizit auftretende Funktionale, sondern um eine höhere Stufe
der Abstraktion. In einem Ausdruck kann man nicht nur von Werten abstrahieren, sondern auch von ganzen Teilausdrücken — selbst Funktionen. Das folgende Beispiel macht das Prinzip deutlich:
?: abs’ ( quadrat 3.0 - quadrat (3.0 + 0.01) ) < 0.1
True
Abstrahiert man von den Werten, kann man das in mathematischer Scheibweise
so ausdrücken:
| x2 - (x + δ)2 | < ε
oder als Definition in HASKELL:
> genuegendKleinQuadrat x delta epsilon =
>
(quadrat x - quadrat (x+delta) ) < epsilon
Offensichtlich ist wäre es nützlich, auch von der speziellen Funktion quadrat
abstrahieren zu können. Genau das kann man mit Funktionen höherer Ordnung
machen: Der mathematische Ausdruck:
Abstraktion von
Funktionen (oder
Verfahren) führt
zu allgemeineren
Funktionen:
Funktionalen
(Funktionen höher
Ordnung)
| f(x) - f(x + δ) | < ε
kann in HASKELL unmittelbar mit f als Argument — deshalb nennen wir die
Funktion Funktional oder Funktion höherer Ordnung — definiert werden:
> genuegendKlein f x delta epsilon =
>
abs’ (f x - f (x+delta) ) < epsilon
Den oben berechneten Ausdruck mit den Werten x = 3.0, epsilon = 0.01 und
delta = 0.1 schreibt man jetzt einfach:
18
Fallunterscheidungen
?: genuegendKlein quadrat
True
3.0
0.01
0.1
Das Wesen der funktionalen Abstraktion besteht darin, ein allgemeineres Problem zu lösen, von dem das ursprüngliche ein Spezialfall ist.
Abstraktion von Funktionen ist ganz offensichtlich ein kraftvolles Programmierprinzip. Wir werden davon noch oft Gebrauch machen. Später wird von einem
anderen, ebenso wichtigen Prinzip der Entwicklung von Software die Rede sein:
Datenabstraktion, eine Technik zur Abstraktion von der Repräsentation von
Daten.
2.7 Fallunterscheidungen
Fallunterscheidungen
gehören zu den
wichtigsten Konstrukten von Programmiersprachen.
Wir haben bereits im vorigen Abschnitt eine Fallunterscheidung verwendet.
Fallunterscheidungen gehören zu den wichtigsten Sprachkonstrukten, die zur
Definition von Funktionen verwendet werden. Sie finden sich in ähnlicher Form
in allen Programmiersprachen. Um etwas anspruchsvollere Beispiele für Funktionsdefinitionen angeben zu können, sollen Fallunterscheidungungen schon hier
eingeführt werden.
In Programmen ist es wie im richtigen Leben oft nötig, Entscheidungen auf der
Basis von bekannten Tatsachen zu treffen.
Das vielleicht einfachste Programmbeispiel ist der Test, ob ein Wert x kleiner als
0 ist.
Der Absolutwert einer Zahl x berechnet sich z.B. so:
wenn x < 0 dann -x sonst x
Beachte: jeder Zweig der Fallunterscheidung, und damit der gesamte Ausdruck,
liefert einen Wert1. In HASKELL notiert man die Fallunterscheidung folgendermaßen:
> abs’ x =
>
if x < 0 then -x else x
?: abs’ (-7)
7
Wohlgemerkt: Fallunterscheidungen liefern einen Wert und gehören deshalb zu
den Ausdrücken der Sprache. Die Fallunterscheidung hat also die Syntax:
1. In anderen Programmiersprachen ist das nicht immer der Fall.
Vers. 0.2 / 10-98
19
Grundlegende Begriffe: Funktionen
if
<Ausdruck_der_Wahrheitswert_liefert> then <Wert1> else <Wert2>
<Wert1> und <Wert2> müssen den gleichen Typ haben, sonst enthielte der Werteberecht des if-Ausdrucks Elemente unterschiedlichen Typs.
Fallunterscheidungen können in HASKELL auch durch sogenannte Wächter ( | )
ausgedrückt werden. Jeweils eine Bedingung ’bewacht’ einen Ausdruck, der nur
dann für die Berechnung des Werts der Fallunterscheidung verwendet wird,
wenn die Bedingung erfüllt ist. Ist mehr als eine erfüllt, wird der erste Ausdruck
verwendet, für den die Bedingung zutrifft. Deshalb heißen Fallunterscheidungen
auch bedingte Ausdrücke (conditional expressions).
Dazu ein weiteres kleines Beispiel:
> max’ x y
>
| x >= y
>
| x < y
= x
= y
?: max’ (-17) 12
12
Die Fallunterscheidung zur Berechnung der größeren von zwei Zahlen ist vollständig: alle Möglichkeiten sind explizit genannt. In der folgenden Formulierung
ist das nicht so. Alle restlichen Fällen — im Beispiel gibt es nur einen nicht
explizit behandelten Fall, nämlich x ist gleich y — werden hinter otherwise
zusammengefaßt:
> max’’ x y
>
| x > y
= x
>
| x < y
= y
>
| otherwise = x
Fallunterscheidungen sollen möglichst disjunkt und vollständig sein. Eine Fallunterscheidung ist disjunkt, wenn es keine zwei überlappenden Fälle gibt. Beispiele für Überlappung sind : x > 0 und x > 10 oder x >= 0 und x == 0.
Im zweiten Beispiel wird die zweite Alternative x == 0 nie erreicht, da sie im
vorherigen x >= 0 enthalten ist. Manche Übersetzer bzw. Interpretierer von
Programmiersprachen weisen Alternativen, die nicht erreichbar sind, zurück.
PROGRAMMIERSTIL:
Fallunterscheidungen sollen vollständig und disjunkt sein.
Vollständigkeit erzwingt man gegebenenfalls mit otherwise.
Ein Fall darf nicht in einem anderen enthalten sein.
20
Fallunterscheidungen
Eine nützliches, in vielen Programmiersprachen anzutreffendes Konstrukt für
Fallunterscheidungen ist case. Für die Maximumsbestimmung sieht das so aus:
> maxCase x y =
>
case (x >= y) of
>
True -> x
>
False -> y
?: maxCase 53 (-(-232))
232
-- warum soviele Klammern?
Der Wert des nach dem reservierten Wort case stehenden Ausdrucks — hier
(x>=y) — steuert die Alternativen. Jeder mögliche Wert — hier nur True und
False — führt zur Berechnung eines Wertes, dem des gesamten case-Ausdrucks. Das ist in diesem Fall eines der Argumente x und y selbst. Auch für
case ist eine abschließende Bedingung otherwise möglich, die alle restlichen
Fälle abfängt. Die Werte aller Alternativen müssen gleichen Typ haben.1 Dies ist
gleichzeitig der Typ des gesamtem case-Ausdrucks.
Übungen
1.
2.
3.
4.
5.
Definiere die Funktion signum, die -1 liefert, wenn ihr Argument eine negative Zahl
ist, 0 sonst.
Der Ausdruck f x . g y bedeutet:
a f ( x . (g y))
b f (x . g) y
c ((f x) . g) y
d (f x) . (g y)
Definiere unter Verwendung von quadrat eine Funktion hochVier.
Argumentbereich für hochVier seien die ganzen Zahlen, Wertebereich die natürlichen Zahlen. ist die Funktion
a total
b surjektiv
c injektiv?
Welche Funktionen besitzen keine Inverse?
1. Warum?
Vers. 0.2 / 10-98
21
Grundlegende Begriffe: Funktionen
6.
a) Entwickeln Sie eine Haskellfunktion abl , die für eine beliebige differenzierbare
Funktion f :: Float -> Float den Wert der Ableitung an der Stelle x annähert. Der Differenzenquotient an der Stelle x0 für eine differenzierbare Funktion f ist:
(f(x0+dx) - f(x0) ) / dx
b) Schreiben Sie eine Funktion
ablDiff::Float-> Float -> (Float->Float)->(Float->Float)
-> Float-> Float
, die die absolute Differenz der obigen Approximation und der tatsächlichen Ableitung berechnet.
Wenden Sie die Funktion für dx = 0.01 , x = 3.0 auf die folgenden Funktionen an:
(1) f(x) = x2 mit f’(x) = 2*x
(2) f(x) = log x
mit f’(x) = 1/x (Bibliotheksfunktion: log)
(3) f(x) = sqrt(x), x >= 0 mit f’(x) = 1/(2*sqrt(x)) (Bibliotheksfunktion sqrt)
(4) f(x) = ex mit f’(x) = ex (Bibliotheksfunktion exp )
22