Aussagenlogik
Werbung
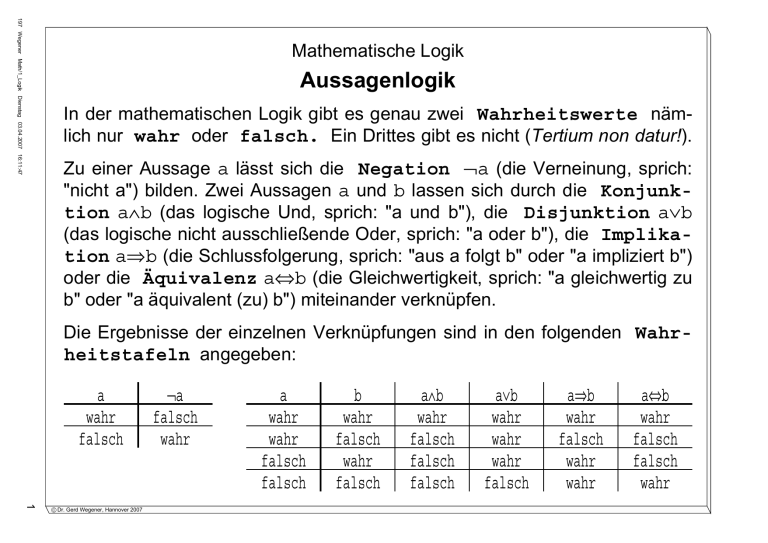
197 Wegener Math/1_Logik Dienstag 03.04.2007 16:11:47 Mathematische Logik Aussagenlogik In der mathematischen Logik gibt es genau zwei Wahrheitswerte nämlich nur wahr oder falsch. Ein Drittes gibt es nicht (Tertium non datur!). Zu einer Aussage a lässt sich die Negation ¬a (die Verneinung, sprich: "nicht a") bilden. Zwei Aussagen a und b lassen sich durch die Konjunktion a∧b (das logische Und, sprich: "a und b"), die Disjunktion a∨b (das logische nicht ausschließende Oder, sprich: "a oder b"), die Implikation a⇒b (die Schlussfolgerung, sprich: "aus a folgt b" oder "a impliziert b") oder die Äquivalenz a⇔b (die Gleichwertigkeit, sprich: "a gleichwertig zu b" oder "a äquivalent (zu) b") miteinander verknüpfen. Die Ergebnisse der einzelnen Verknüpfungen sind in den folgenden Wahrheitstafeln angegeben: a wahr falsch 1 © Dr. Gerd Wegener, Hannover 2007 ¬a falsch wahr a wahr wahr falsch falsch b wahr falsch wahr falsch a∧b wahr falsch falsch falsch a∨b wahr wahr wahr falsch a⇒b wahr falsch wahr wahr a⇔b wahr falsch falsch wahr Mathematische Logik Aussagenlogik Die Konjunktion ist also nur dann wahr, wenn beide Aussagen wahr sind, während die Disjunktion wahr ist, wenn eine oder beide der verknüpften Aussagen wahr sind. Nur die Implikation, aus etwas Wahrem etwas Falsches zu schließen, ist falsch. Alle anderen Implikationen sind wahr. Man sagt auch aus Unsinn kann alles geschlossen werden. Folgende Zusammenhänge bestehen zwischen den Verknüpfungen: a⇒b ⇔ ¬a∨b ¬(a∧b) ⇔ ¬a∨¬b a⇒b ⇔ ¬b⇒¬a ¬(a∨b) ⇔ ¬a∧¬b Die letzten zwei Beziehungen werden auch Regel von de Morgan genannt. Beispiel: Es regnet und die Sonne scheint. (Dann gibt es einen Regenbogen!) Das negiert: Es regnet nicht oder die Sonne scheint nicht. (Dann gibt es keinen Regenbogen!) © Dr. Gerd Wegener, Hannover 2007 2 Mathematische Logik Aussagenlogik Wenn man sich nicht sicher ist, ob eine zusammengesetzte Aussage wahr ist, prüft man diese mit Hilfe einer Wahrheitstafel, in der alle möglichen Kombinationen von Wahrheitswerten der benutzten Variablen ausprobiert werden. a wahr wahr falsch falsch a wahr wahr falsch falsch © Dr. Gerd Wegener, Hannover 2007 b wahr falsch wahr falsch b wahr falsch wahr falsch c=(a⇒b) wahr falsch wahr wahr c=(a⇒b) wahr falsch wahr wahr ¬a falsch falsch wahr wahr ¬a falsch falsch wahr wahr d=(¬a∨b) wahr falsch wahr wahr c⇔d wahr wahr wahr wahr ¬b d=(¬b⇒¬a) falsch wahr wahr falsch falsch wahr wahr wahr c⇔d wahr wahr wahr wahr 3 Mathematische Logik Aussagenlogik Die folgenden Wahrheitstafeln beweisen die Regel(n) von de Morgan. a wahr wahr falsch falsch b wahr falsch wahr falsch a∧b wahr falsch falsch falsch c=¬(a∧b) falsch wahr wahr wahr ¬a falsch falsch wahr wahr ¬b d=(¬a∨¬b) falsch falsch wahr wahr falsch wahr wahr wahr c⇔d wahr wahr wahr wahr a wahr wahr falsch falsch b wahr falsch wahr falsch a∨b wahr wahr wahr falsch c=¬(a∨b) falsch falsch falsch wahr ¬a falsch falsch wahr wahr ¬b d=(¬a∧¬b) falsch falsch wahr falsch falsch falsch wahr wahr c⇔d wahr wahr wahr wahr © Dr. Gerd Wegener, Hannover 2007 4 Mathematische Logik Prädikatenlogik Logische Aussagen haben zwar einen Wahrheitswert, aber keinerlei Bezug zu den Objekten der Welt. Um also Aussagen über Objekte (z.B. Zahlen) zu machen, bedarf es sog. Quantoren. Will man ausdrücken, dass für alle Elemente a einer Menge A ein bestimmtes Prädikat (=Aussage) P(a) gilt, so schreibt man das folgendermaßen: ∀ P(a) a∈A Das Zeichen ∀ wird auch Allquantor genannt (sprich: "für alle"). Soll notiert werden, dass es mindestens ein Element a einer Menge A gibt, für das ein bestimmtes Prädikat P(a) gilt, so schreibt man das folgendermaßen: ∃ P(a) a∈A Das Zeichen ∃ wird auch Existenzquantor genannt (sprich: "es gibt"). © Dr. Gerd Wegener, Hannover 2007 5 P(a) ∃ P(a) ∀ Mathematische Logik Prädikatenlogik Für beide Quantoren gilt ¬( ∀ P(a)) a∈A ⇔ ∃ ¬P(a) a∈A In Worten: Die Negation von für alle a aus A gilt P(a) ist gleichwertig zu es gibt ein a aus A, so dass P(a) nicht gilt. Beispiel: Das Gegenteil der Aussage alle Kreter sind Lügner lautet es gibt (mindestens) einen Kreter, der kein Lügner ist. © Dr. Gerd Wegener, Hannover 2007 6 ¬( ∀ P(a)) ⇔ ∃ ¬P(a) Mathematische Logik Definitionen, Sätze und Beweise In der Mathematik beschäftigt man sich mit Objekten des Denkens, die zwar aus der realen Welt abstrahiert (abstrahere = (etwas) abstreifen) sind, innerhalb der Mathematik jedoch keinerlei Bezug zur Welt außerhalb benötigen. Zuerst legt man die Objekte, von denen man spricht, in einer Definition fest. Dann formuliert man Aussagen oder Sätze über diese Objekte. Anschließend muss man für jeden Satz einen Beweis angeben, bei dem man sich natürlich auf bereits bewiesene Sätze stützen kann. Einige grundlegende Sätze muss man jedoch meistens voraussetzen, die man nicht beweisen will oder kann. Diese Sätze werden Axiome genannt. © Dr. Gerd Wegener, Hannover 2007 7 Mathematische Logik Definitionen, Sätze und Beweise Ein Beweis ist nichts Anderes als eine Kette von Schlussfolgerungen, die mit einer unbestritten wahren Aussage beginnt und bei der behaupteten Aussage endet. Diese muss dann nämlich wahr sein (wenn man richtig geschlossen hat), da aus etwas Wahrem nur etwas Wahres gefolgert werden kann. Manchmal gelingt es nicht, eine solche Beweiskette zu führen. Dann kann man auch mit der Negation der behaupteten Aussage beginnen und versuchen, durch korrekte Schlussfolgerungen auf einen Widerspruch zum Anfang zu kommen. Wenn die Negation einer Aussage falsch ist, so schließt man, muss diese richtig sein. (Nicht alle Mathematiker erkennen diese Beweismethode an. Deswegen ist es immer besser, einen direkten Beweis zu haben.) © Dr. Gerd Wegener, Hannover 2007 8 Mathematische Logik Beweis durch Widerspruch Im folgenden der Beweis für den Euklidischen Satz gegeben, dass es unendlich viele Primzahlen gibt. Satz: Es gibt unendlich viele Primzahlen. Beweis: Angenommen, es gäbe endlich viele Primzahlen und ihre Anzahl sei n. Dann bezeichnen wir diese mit p1, p2, p3, ... pn. Wir bilden nun das Produkt p aller dieser Primzahlen und zählen eins dazu. p = p1·p2·p3·...·pn q = p + 1 Die Zahl p ist durch alle Zahlen pi (1≤i≤n) teilbar. Die Zahl q hingegen ist durch keine Zahl pi teilbar. Deswegen muss es selbst eine Primzahl oder mindestens durch eine -bisher unbekannte- teilbar sein. Das aber steht im Widerspruch zur Ausgangsannahme, womit der Satz bewiesen ist. (Man schreibt dann q.e.d. (= quod erat demonstrandum = was zu beweisen war (manche schreiben auch w.z.b.w.)) und versucht, möglichst cool dreinzuschauen.) 9 © Dr. Gerd Wegener, Hannover 2007 Beweis durch vollständige Induktion Im folgenden ist ein Beweis für die Formel von Gauß über die Summe der Zahlen von 1 bis n gegeben. ∀ Satz: n ∑i = n∈IN i=1 Beweis: n·(n+1) 2 Die Formel ist richtig für n=1. Sei sie richtig für ein n>0, dann ist n+1 n ∑ i = ∑ i + (n+1) = i=1 i=1 = n·(n+1) 2 + (n+1) = n·(n+1)+2·(n+1) 2 = (n+2)·(n+1) 2 (n+1)·((n+1)+1) 2 Die Formel gilt offensichtlich auch für n+1. Dann gilt sie auch für n+2, n+3, n+4, etc. (q.e.d.) Der Schluss wenn etwas für ein n richtig ist, dann ist es auch für n+1 richtig, zusammen mit es ist für n=1 richtig, woraus folgt dann ist es für alle n richtig, heißt Beweis durch vollständige Induktion. © Dr. Gerd Wegener, Hannover 2007 10 ∀ Mathematische Logik n ∑i = n·(n+1)











