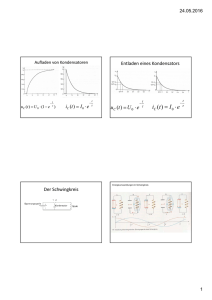
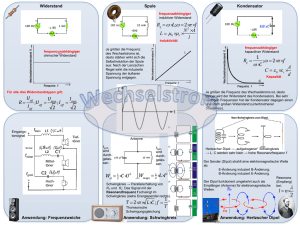
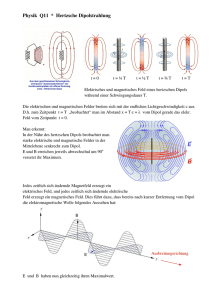
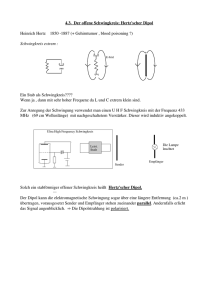
Vom Schwingkreis zum strahlenden Dipol
Werbung

Vom Schwingkreis zum strahlenden Dipol Im Jahr 1886 entdeckte der Physiker Heinrich H ertz die elektro­ magnetischen Wellen. Wir nutzen sie heute auf vielfältige Weise: Bei Rundfunk, Fernsehen oder Handy übertragen sie Daten, im Mikro­ wellenherd erhitzen sie Speisen. Dreipunktschaltung zur Erzeugung ho­ her Frequenzen: Der Schwingkreis besteht aus einer Spule mit 13 Windungen der Länge 11 cm und 3 cm Durchmesser. Ihre Induktivi­ tät ist also L = µ 0 µ r n 2 A/l = 1,36 · 10 − 6 H. Die beiden Kapazitäten C 1 ≈ 50 pF und C 2 = C GD bilden die Schwingkreiskapazität C = 25 pF (als Reihenschaltung). C GD ist die Kapazität zwischen Gate G und Drain D des FET-Tran­ sistors (hier z. B. VN88AFD). V 1 Sie entziehen sich aber unserer unmittelbaren Wahrnehmung. Schall­ wellen sind dagegen hörbar, Seilwellen sogar sichtbar. Diese mecha­ nischen Wellen brauchen materielle Träger, elektromagnetische ­Wellen kommen dagegen als Schwingungen des E- und B-Vektors ohne jedes Medium aus. Doch zeigen sich formale Ähnlichkeiten zu mechanischen Wellen. So ist ihre Ausbreitungsgeschwindigkeit end­ lich. Analogien beider Wellenarten begegnen uns in diesem Kapitel auch bei stehenden Wellen sowie bei Eigenschwingungen. Wie entstehen elektromagnetische Wellen? An unserem Radio lesen wir für verschiedene Sender hohe Frequenzen ab. Wir müssen also sehr schnelle Schwingungen erzeugen. 1. Erzeugung hochfrequenter Schwingungen Zur Erzeugung hochfrequenter elektromagnetischer Schwingungen braucht man nach der thomsonschen Gleichung Schwingkreise möglichst kleiner Kapazität und Induktivität. Man benutzt dazu meist die so genannte Dreipunktschaltung ‹ V 1 . Der Schwingkreis dort hat für C = 25 pF und L = 1,36 · 10 −6 H die Eigenfrequenz 1 _______ 1 __________________________ 1___ ___ 1 f 0 = __ = _________________________ = 27 MHz. = T 2 π √ L C 2 π √ 1,36 · 10 −6 H · 25 · 10 −12 F Schaltungsaufbau nach ‹ V 1 : C 1 ≈ 50 pF ist hier ein Schwingquarz. B 1 Einen Versuchsaufbau dazu zeigt ‹ B 1 . Als Kondensator der Kapa­ zität C 1wird hier ein Schwingquarz von etwa 50 pF verwendet. Bei ihm befindet sich zwischen den Kondensatorplatten ein Quarzplätt­ chen. Es hat eine bestimmte Dicke, sodass es bei der Frequenz f = 27,120 MHz mechanisch in Resonanz zum Oszillator schwingt. Es zwingt sogar dem Oszillator seine Frequenz auf, wenn dieser nach der thomsonschen Gleichung eine Frequenz in der Nähe der Quarzfrequenz hat ‹ Vertiefung. In ‹ V 2 wird die Oszillatorschwingung mit einem Prüfkreis nach­ gewiesen. Dieser ist ein Schwingkreis aus einer Spule mit Lämpchen und einem Drehkondensator einstellbarer Kapazität. Seine flache Spule wird dazu zwischen die Windungen der Oszillatorspule ge­ schoben. Das magnetische Wechselfeld durchsetzt teilweise diese Flachspule und erzeugt in ihr durch Induktion Wechselströme der Oszillatorfrequenz. Prüfkreis aus Drehkondensator (30 … 100 pF) und Flachspule (3 Windungen) mit Glühlämpchen (2,5 V/0,1 A). Der Prüf­ kreis ist hier am Drehkondensator auf ­Resonanz abgestimmt (f = 27,12 MHz). V 2 152 Das Glühlämpchen in diesem Kreis leuchtet besonders hell, wenn dessen Frequenz mit der des Oszillators übereinstimmt (f = 27,10 MHz). Man erreicht dies durch Verändern der Kapazität des Drehkonden­ sators. In ‹ B 2 sind zur Erzeugung noch höherer Frequenzen die Kapazi­ täten C 1 und C 2 weiter verringert. Die Schwingkreiskapazität C ­beträgt dort weniger als 5 pF. Außerdem ist die Windungszahl der Oszillatorspule so weit verringert, dass nur noch eine einzige Win­ dung übrig bleibt. Bei einem Windungsdurchmesser von 3 cm schwingt der so aufgebaute Oszillator ‹ B 3 mit etwa 400 MHz. Elektromagnetische Wellen Vom Schwingkreis zum strahlenden Dipol Der Prüfkreis in ‹ B 3 besteht aus zwei 1-Cent-Stücken und einer Drahtschleife mit einem Lämpchen (2,5 V; 0,1 A) in seiner Mitte. Um ihn auf Resonanz mit der Oszillatorfrequenz abzustimmen, ver­ ändert man den Abstand der Kondensatorplättchen geringfügig. 2. Schwingungen in einer Dreipunktschaltung Bei der Meißnerschaltung wird die Steuerspannung zum Schalten des Transistors durch Induktion in einer Rückkopplungsspule er­ zeugt. Bei der Dreipunktschaltung ‹ V 1 benutzt man stattdessen die Teilspannung U zwischen Punkt 1 und 3 der Schwingkreisspule. B 2 Schaltung für sehr hohe Frequenzen Die Rückkopplung geschieht folgendermaßen: Die Schwingkreis­ spule liegt mit ihren Anschlüssen 1 und 2 an den in Reihe geschal­ teten Kondensator C 1 und C 2, die zusammen die Kapazität C des Schwingkreises bilden. Die Teilspannung U (t) zwischen Punkt 1 und 3 wird zur Rückkopp­ lung genutzt. Vom Minuspol der Quelle (U 0) aus gesehen, hat Punkt 3 das Potential U 0, Punkt 1 also U 0 + U (t). Über den Konden­ sator der Kapazität C 1 gelangt nur der Wechselspannungsanteile U (t) an die Steuerelektrode G des Transistors. Ist der Schwing­ kreiskondensator also gerade entladen (U 1, 2 = 0), so hat Punkt 1 das Potential U 0; die Steuerelektrode G hat davon unbeeinflusst das am Potentiometer voreingestellte Potential U V. Wird nun der Kondensator C 1 oben positiv geladen, so erhöht sich das Potential an 1 um U (t). Dadurch wird über C 1auch das Poten­tial an G erhöht. Der Transistor wird leitend und führt dem Schwingkreis Energie zu, so wie bei der Meißner-Schaltung. Wird die obere Kon­ densatorplatte negativ, so wird das Potential an G verringert, der Transistor sperrt. 400 MHz-Oszillator. Die Glühlampe im Prüfkreis leuchtet hell, wenn dieser auf die Oszillatorfrequenz abgestimmt ist. B 3 Vertiefung Der Schwingquarz ‹ B 4 zeigt vereinfacht einen Quarzkristall (SiO 2). Die roten Kugeln (1, 3, 5) bedeuten Si 4+-Ionen, die blauen (2, 4, 6) je zwei O 2−-Ionen. In einem äußeren, nach unten gerichteten Feld werden die Si 4+-Ionen nach ­unten, die O 2−-Ionen nach oben verschoben. Dabei drängt sich Ion 1 zwischen 2 und 6, Ion 4 zwischen 3 und 5 ‹ B 4 b . Der Kristall wird etwas breiter und nied­ riger. Bei umgekehrter Feldrichtung wird er höher und schmaler. Solche Schwingquarze lassen sich im elek­ trischen Wechselfeld bei passender Frequenz zu mecha­ nischen Resonanzschwingungen anregen. Sie geben Quarzuhren ihre enorme Präzision. a) Berechnen Sie in ‹ B 1 die Kapazität C 2 = C GD des Transistors. b) Die Kapazitätsangaben auf Kondensatoren sind meist ungenau (±20 bis ±30 %). Erläutern Sie, wie Sie für die Frequenz f = 27 MHz A 1 Schwingquarz a) normal, b) deformiert, c) im Glas­ gehäuse B 4 im Fall einer zu kleinen Kapazität dies durch die Induktivität mög­ lichst einfach korrigieren können. c) Bestimmen Sie nach ‹ V 1 die Induktivität L so, dass f = 13,5 MHz ist. Der Abstand der Cent-Stücke des Resonanzkreises in ‹ B 3 wird halbiert. Beurteilen Sie die Ände­ rung der Kapazität, der Induktivität und der Eigenfrequenz des Schwing­ kreises. A 2 Vom Schwingkreis zum strahlenden Dipol Elektromagnetische Wellen 153 B 1 Elektromagnetische Schwingung eines Leiters nach dem Berühren seines Endes mit einem geladenen Stab 3. Der Hertz-Dipol Bringt man nach ‹ B 1 einen geladenen Stab nahe genug an das Ende des isoliert aufgehängten 5 m langen Drahtes, so springt – hörbar durch einen winzigen Funken – Ladung auf diesen über. Die Induk­ tionsschleife am Speicheroszilloskop registriert einen abklingenden hochfrequenten Wechselstrom der Frequenz 30 MHz. Ein gerader Leiter kann also offensichtlich eine elektromagnetische Eigen­ schwingung ausführen. Wie kommt es dazu? Wir entwickeln dies an einem Schwingkreis für 434 MHz, ‹ V 1 und ‹ B 2 . Die Drahtschleife des Schwingkreises in ‹ B 2 a hat einen Durch­ messer von 5 cm. Zwei 1-Cent-Stücke an den Enden bilden den Plat­ tenkondensator. Bei etwa 5 mm Abstand zwischen den Platten leuchtet das Lämpchen besonders hell ‹ V 1 a . Wir beobachten sogar Resonanz, wenn wir auf die Plättchen ganz verzichten und dafür die Drahtschleife noch etwas länger wählen ‹ V 1 b und ‹ B 2 b . Wir biegen die Drahtschleife noch weiter aus­ einander, bis wir schließlich einen geraden Leiter erhalten ‹ B 2 c . Kann auch er zu Resonanzschwingungen angeregt werden? Zu Resonanzschwingungen mit einem Dezimeterwellensender (links) angeregt: a) Schwingkreis, b) offene Drahtschleife, c) Dipol, in dessen Mitte eine Glühlampe Wechselströme anzeigt, d) Dipol, an dessen Enden eine Glimmlampe elektrische Wechsel­ felder anzeigt. B 2 ‹ B 2 Wir bringen den Schwingkreis mit Lämpchen (2,5 V/0,1 A) nahe an die Oszilla­ torspule und verändern geringfügig den Ab­ stand der Kondensatorplatten, bis das ­Lämpchen hell leuchtet. b) Ohne Kondensator­ platten muss die Schleife etwa den doppelten Durchmesser haben um ein helles Leuchten einzustellen. c) Das Lämpchen leuchtet auch in einem geraden Draht bzw. Metallstab ­richtiger Länge (der Stab kann durch über­ geschobene Hülsen in der Länge verändert werden). d) Um elektrische Felder aufzu­ spüren, überstreichen wir mit einer Glimm­ lampe den Stab. In der Mitte ist sie dunkel, an den Enden leuchtet sie am hellsten. V 1 154 In ‹ V 1 c bringen wir in die Nähe der Oszillatorspule einen leiten­ den Stab, dessen Länge durch übergeschobene Metallhülsen verän­ dert werden kann. Bei der Länge l = 34 cm leuchtet das in der Mitte des Stabes eingebaute Lämpchen besonders hell. Der Stab schwingt also bei l = 34 cm in Resonanz. Doch wo ist bei diesem Stab der Kondensator mit seinem elektrischen Feld, wo die Spule mit Magnet­ feld geblieben? Die in ‹ V 1 d benutzte Glimmlampe zeigt nicht den Strom im Stab, sondern die Ladung auf ihm. Sie bleibt in der Mitte des Stabes dun­ kel, an seinen Enden leuchtet sie jedoch ‹ B 2 d . Für die im Stab hin- und herschwingenden Elektronen gibt es an dem einen Stab­ ende kein Weiterkommen, am anderen fehlt der Nachschub. In der einen Stabhälfte häufen sie sich, in der anderen herrscht Mangel. An den Stabenden entstehen also im ständigen Wechsel Plus- und ­Minuspole. Deshalb wird der stabförmige Schwinger Hertz-Dipol genannt (nach Heinrich H ertz , 1857 – 1894). An den Stabenden ist die Ladungsanhäufung am größten. Dort herr­ schen starke elektrische Felder. Die Stromstärke ist dort jeweils null. Dagegen ist die Stromstärke in der Mitte maximal, also auch das den Strom umgebende Magnetfeld. Spule und Kondensator sind beim Dipol nicht mehr getrennt. Magnetische und elektrische Felder grei­ fen fließend ineinander. Elektromagnetische Wellen Vom Schwingkreis zum strahlenden Dipol 4. Faradays Feldidee bestätigt sich Der Dipol lässt sich ebenso zu Schwingungen anregen wie der ge­ schlossene Schwingkreis. Was ist das Besondere am Dipol? In ‹ V 2 a bringt die Oszillatorschleife O das Lämpchen des Dipols E nur zum Leuchten, wenn dieser sich in unmittelbarer Nähe der Schleife befindet. Fügen wir aber nach ‹ V 2 b zusätzlich den Dipol S ein, so zeigt das Leuchten des Lämpchens in Dipol E auch in ­größerer Entfernung noch kräftige Schwingungen. Warum? S wird wie ein geschlossener Schwingkreis zum Schwingen angeregt. Im Schwingkreis war das elektrische Feld auf den kleinen Bereich zwischen den Kondensatorplatten konzentriert, das magnetische praktisch auf die Spule. Das elektrische und das magnetische Feld des langgestreckten Dipols S reichen aber weit nach außen. Wir ­nennen ihn deshalb Sendedipol S. Mit dem Empfangsdipol E registrieren wir auch noch in großem Abstand vom Sendedipol S die von ihm ausgehenden Wechselfelder. ‹ V 2 c zeigt, wie die Amplitude E dieser elektrischen Wechselfelder mit dem Abstand abnimmt. Was erwarten wir nach bisherigen Kenntnissen? a) Wir vergrößern den Abstand des ­Dipols E zur Oszillatorschleife O. Sein Lämpchen er­ lischt. b) Es leuchtet erneut, wenn wir nahe der Schleife O den weiteren Dipol S einfügen. c) Wir ersetzen das Lämpchen in E durch ein 10 V-Drehspulinstrument. Da es dem hoch­ frequenten Wechselstrom nicht folgen kann, schalten wir eine Gleichrichterdiode parallel. Jetzt können wir mit dem Instrument Feld­ stärken vergleichen. Im Abstand r = 0,2 m vom Sender messen wir etwa 10 V; bei r = 2 m noch etwa 1 V, also ein Zehntel der Feldstärke und nicht ein Tausendstel, wie nach dem Cou­ lomb-Gesetz und ‹ B 3 erwartet würde. V 2 Nach ‹ B 3 seien die Enden eines Dipols der Länge l entgegen­gesetzt __› geladen. Der Vektor der elektrischen Feldstärke E in__einem Punkt P __› › der Mittelachse setzt sich aus den Komponenten E 1 und E 2 zu­ sammen. Den ähnlichen Dreiecken entnehmen wir die Beziehung E/E 1 = l/r; daraus folgt E = E 1 l/r. Nach dem Coulomb-Gesetz ist ­außerdem E 1 = 1/r 2. Also gilt für die im Punkt P herrschende elek­ trische Feldstärke dieses elektrostatischen Feldes E ~ 1/r 3. Die Ladungen des Dipols erzeugen im __› Punkt P die elektrische Feldstärke E . B 3 Um dies zu prüfen, vergrößern wir in ‹ V 2 c den Abstand des ­Empfangsdipols E vom Sendedipol S auf das Zehnfache. Die Emp­ fangsfeldstärke müsste nach E ~ 1/r 3 auf den tausendsten Teil zu­ rückgehen. Dies tritt aber überraschenderweise nicht ein. Selbst wenn wir den Abstand noch weiter vergrößern, geht die Amplitude der hochfrequenten elektrischen Feldstärke nicht so stark zurück wie die Feldstärke des elektrostatischen Dipolfeldes in ‹ B 3 . Was also liefert dort das starke E-Feld? Der Strom im Dipol erzeugt ein sich schnell veränderliches B-Feld. Es induziert elektrische Feld­ linien. Wie wir von elektrischen Wirbelfeldern wissen, sind sie in sich geschlossen. Sie lösen sich also von den Dipolladungen und erobern den Raum um den Dipol. Faraday nahm an, dass alle Felder zum Ausbreiten im Raum Zeit brauchen, also eine endliche Geschwindigkeit haben. Er dachte ­bereits an eine wellenförmige Ausbreitung ähnlich wie bei Schall­ wellen ‹ Interessantes. Interessantes F araday mit Weitblick Faraday legte am 12. März 1832 folgen­ den Gedanken schriftlich bei der Royal ­Society in London nieder: „Gewisse Ver­ suchsergebnisse bringen mich zu der Über­ zeugung, dass sich magnetische Wirkun­ gen ausbreiten und dafür Zeit benötigen. … Ich meine, dass sich die Wellentheorie auf diese Erscheinungen ebenso anwenden lässt wie auf den Schall und sehr wahr­ scheinlich auch auf Licht. Ich denke, dass die Wellentheorie analog dazu auf die Er­ scheinungen der elektrischen Induktion (gemeint ist das elektrische Feld) ange­ wandt werden kann …“ Merksatz Ein Sendedipol hat weitreichende elektrische Wechselfelder um sich. Sie können mit dem Coulomb-Gesetz, also mit den Ladungen des Dipols, nicht erklärt werden. Vielmehr entstehen Sie durch Induk­ tion aus den sie begleitenden Magnetfeldern. n Formulieren Sie eine Hypothese über den Zusammenhang von Dipollänge und dessen Eigenfrequenz. Begründen Sie diese. A 1 Vom Schwingkreis zum strahlenden Dipol Elektromagnetische Wellen 155