Zwischenklausur zur Mathematik A, WiSe 11/12

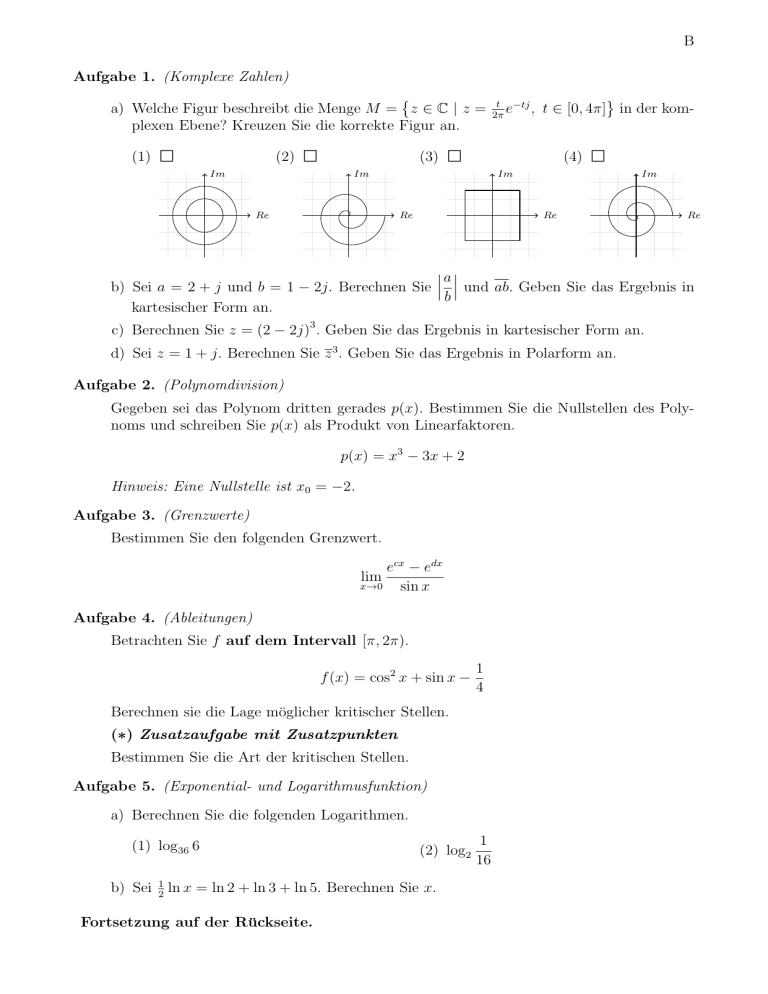
B
Aufgabe 1. (Komplexe Zahlen)
a) Welche Figur beschreibt die Menge M = z ∈ C | z =
plexen Ebene? Kreuzen Sie die korrekte Figur an.
(1)
2
(2)
Im
2
(3)
Im
Re
2
t −tj
e ,
2π
t ∈ [0, 4π] in der kom-
(4)
Im
Re
2
Im
Re
Re
a
b) Sei a = 2 + j und b = 1 − 2j. Berechnen Sie und ab. Geben Sie das Ergebnis in
b
kartesischer Form an.
c) Berechnen Sie z = (2 − 2j)3 . Geben Sie das Ergebnis in kartesischer Form an.
d) Sei z = 1 + j. Berechnen Sie z 3 . Geben Sie das Ergebnis in Polarform an.
Aufgabe 2. (Polynomdivision)
Gegeben sei das Polynom dritten gerades p(x). Bestimmen Sie die Nullstellen des Polynoms und schreiben Sie p(x) als Produkt von Linearfaktoren.
p(x) = x3 − 3x + 2
Hinweis: Eine Nullstelle ist x0 = −2.
Aufgabe 3. (Grenzwerte)
Bestimmen Sie den folgenden Grenzwert.
ecx − edx
lim
x→0
sin x
Aufgabe 4. (Ableitungen)
Betrachten Sie f auf dem Intervall [π, 2π).
f (x) = cos2 x + sin x −
1
4
Berechnen sie die Lage möglicher kritischer Stellen.
(∗) Zusatzaufgabe mit Zusatzpunkten
Bestimmen Sie die Art der kritischen Stellen.
Aufgabe 5. (Exponential- und Logarithmusfunktion)
a) Berechnen Sie die folgenden Logarithmen.
(1) log36 6
b) Sei
1
2
(2) log2
ln x = ln 2 + ln 3 + ln 5. Berechnen Sie x.
Fortsetzung auf der Rückseite.
1
16
B
Aufgabe 6. (Winkelfunktionen)
π
. Wie sieht der Graph von f (x) aus?
Gegeben sei die Funktion f (x) = sin2 x +
2
(1)
2
(3)
y
1
π
−π
2
y
1
x
π
−π
−1
(2)
2
x
−1
(4)
y
1
π
−π
2
y
1
x
π
−π
−1
x
−1
Aufgabe 7. (Beträge)
Ordnen Sie den Funktionen jeweils den korrekten Graphen zu. Tragen Sie die Nummer
des zugehörigen Graphen jeweils in das freie Feld ein.
(b) f (x) = |x − 1| − 1
(a) f (x) = ||x − 1| − 1|
y
y
1
y
1
1
x
1
(1)
x
1
(3)
y
1
x
1
(5)
y
y
1
1
x
(2)
1
1
x
x
(4)
(6)
1
Aufgabe 8. (Funktionen)
Gegeben sei die folgende Funktion.
f : R → R, f (x) = −x2 + 2x − 4
Markieren Sie alle korrekten Aussagen.
2
2
2
2
f ist injektiv.
f ist surjektiv.
f ist bijektiv.
f ist weder injektiv noch surjektiv.
2
2
2
2
f ist invertierbar.
f ist gerade.
f ist ungerade.
f ist weder gerade noch ungerade.