4112 1)1(2 =+⋅+ = T 2 4 8 )2( 19 )13( 1 )3( )3( == − − = +− − − =− T

Lösungen zu den Grundwissensaufgaben Algebra – Jahrgangsstufe 7
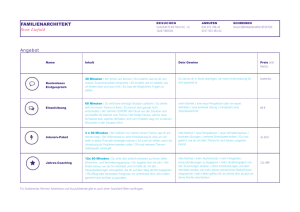
1. Beispiele: T1 (1) = 12 + 2 ⋅ 1 + 1 = 4
T2 (−3) =
(−3) 2 − 1 9 − 1 8
=
= =2
(−3 + 1) 2 ( −2) 2 4
3
4
1
2
1
2
–3
–1,5
n2+2n+1
4
9
4
0,25 2 14
3 1
n 2 −1
( n +1) 2
0
1
3
2
–1
–1
5
16
3
9. a) 4x + 3 = 2x + 9
-2x
2x + 3 = 9 -3
2x = 6
:2
x=3
L={3}
b, 17x – 33 + 12x – 16 = 4x + 56 + 10x
29x - 49 = 14x + 56 -14x
+49
15x - 49 = 56
15x = 105
:15
x=7
L={7}
10. Gesuchte Zahl: x
c) 10 – 3(5 – 4x) = 15x + 40
10 – 15 + 12x = 15x + 40
– 5 + 12x = 15x + 40 -12x
– 5 = 3x + 40 -40
–45 = 3x :3
-15 = x
L = { –15 }
11. Preis pro kg der Mischung: x
50 ⋅ 8 + 150 ⋅ 12 = 200 ⋅ x
6x = 2x + 12
7
2200 = 200x
x=3
2.
3.
Die gesuchte Zahl ist 3.
T(-2;1,5) = (-2)2-(-2) · 1,5+2,5· 1,5 = 4 + 3 + 3,75 = 10,75
T(-2;1,5) = 3 · (-2) – 3(1 – 2·1,5) = -6-3(-2) = -6 + 6 = 0
T(x; y) = 13,60 + (x − 8) · 0,05 + y · 0,15
Hilfe zur Termaufstellung durch Zahlenbeispiele:
Für 20 Nah- und 10 Ferngespräche muss man zahlen: 13,60 + (20 − 8) · 0,05 + 10 · 0,15
Für 30 Nah- und 20 Ferngespräche muss man zahlen: 13,60 + (30 − 8) · 0,05 + 20 · 0,15
4.a
Figur Nr
Anzahl der Plättchen
b, 4n+4 = 68 -4
1
8
2
12
;
3
16
4n = 64
:4
4
20
;
11 = x
1 kg der Mischung kostet 11 €
12. Basiswinkel: x ; Winkel an der Spitze: x – 30
x + x + x − 30 = 180
x = 70
13.
n
4n+4
Produktion
n = 16
Prozentwerte
Winkel im Kreisdiagramm
45
= 36
P = 80 ⋅
100
100% =
ˆ 360°; 1% =ˆ 3,6°
5.
45%
Anzahl der Tische
Anzahl der Personen
1
6
2
10
3
14
4
18
n
4n+2
6. a. Der Flächeninhalt ändert sich nicht.
Zahlenbeispiel: A = 12 (2 + 3) ⋅ 4 = 10 im Vergleich zu A = 12 (2 + 1 + 3 − 1) ⋅ 4 = 10
Eigentliche Begründung: A = 12 (a + 1 + c − 1) ⋅ h = A = 12 (a + c) ⋅ h
b. Der Flächeninhalt verdoppelt sich. (wieder Zahlenbeispiel möglich )
A = 12 (2a + 2c) ⋅ h = A = 2 ⋅ 12 (a + c) ⋅ h
Begründung:
7.
15
= 12
100
43,2°
30
= 24
100
86,4°
10
=8
100
28,8°
Außendienst:
P = 80 ⋅
Verwaltung
P = 80 ⋅
Konstruktion:
P = 80 ⋅
14. 30% von x = 3852€ ; x = 3852€ : 30% = 12 840 €
oder 30% entspricht 3852€ ; 1% entspricht 3852€ : 30= 128,40 € ; 100% entspricht 12 840 €
a) 14mn – 4m² + 5mn – 18mn + 5m² = mn + m²
b) 7ab – ba – 4a²b² – 3ab + 5b²a² = 3ab + a²b²
c) 7a – (3b + 4c) + (2a – 5b) = 7a – 3b - 4c + 2a – 5b = 9a – 8b – 4c
d, 14x – (13 – 17x) + (–21y + 11x – 7) = 14x – 13 + 17x –21y + 11x – 7 = 42x – 21y – 20
15.
f) 18a² – 4a(3a – 2) + 15a² = 18a² – [12a2 –8a] + 15a² = 18a² –12a2 + 8a + 15a² = 21a² + 8a
315
435
= 42% Jungen und
= 58% Mädchen
750
750
16.
106% von x = 143,10€ ; x = 143,10€ : 106% = 135 €
Alter Preis: 135 €; Preiserhöhung: 8,10 €
17.
92,5% von x = 203,50€ ; x = 203,50€ : 92,5% = 220€
Alter Preis: 220,00 € Preissenkung: 16,50 €
e) 5(2a – b) + (a + 3b) . 4 = 10a – 5b + 4a + 12b = 14a + 7b
2
=ˆ 45.3,6° =162°
2
g) (3y – 5)(7y – 11) – (2y – 1)(3y – 4) = 21y – 33y -15y + 55 – [6y - 8y - 3y + 4] =
21y2 – 33y -15y +55 – 6y2+ 8y + 3y – 4 = 15y² – 57y + 51
18.
2
17xy – 32x + 8x y -24xy + 6y = xy – 32x² + 6y²
8.
a) 5a4 – 6a3 + a2 = a2(5 a2 - 6a + 1)
b) –6a2 + 12ab + 8ac = 2a(-3a + 6b + 4c)
c) 3x2y-5x3 y = x2 y( 3 - 5x )
92 110
⋅
= 253 €
100 100
; Der endgültige Preis beträgt 253 €.
Oder : 92% von 250€ = 230€ ; 110% von 230€ = 253€
h) 17xy – (4x + 3y)(8x – 2y) =17xy – [32x2 - 8x y + 24xy -6y2] =
2
P = 250 ⋅
19.
(Oder: Dreisatz wie bei Aufgabe 14)
94% von(110% von x) = 517 €
oder: 94% von x = 517 € ; x = 550 € ; 110% von y = 550 € ; y = 500€
Der ursprüngliche Preis betrug 500 €.