Ablaufen der möglichen Kopfpos. Simulation von M Realisierung

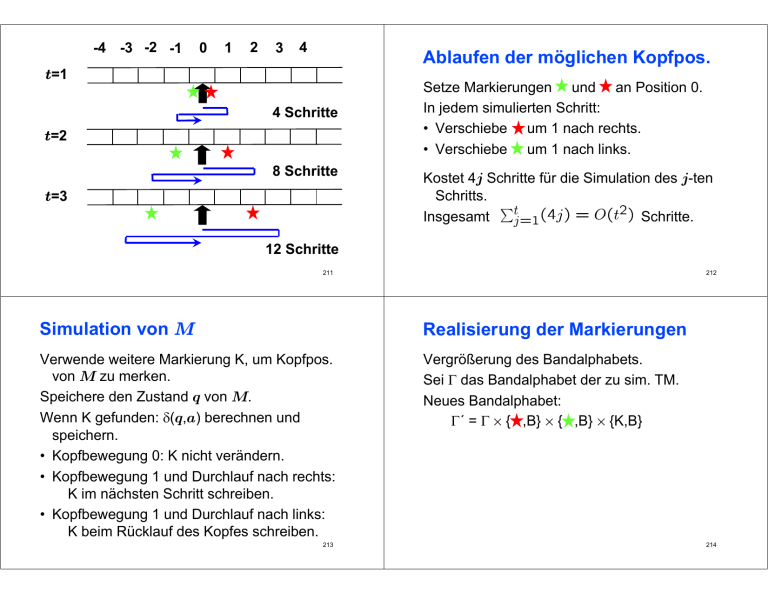
-4 -3 -2 -1
0
1
2
3
4
Ablaufen der möglichen Kopfpos.
t=1
t=2
4 Schritte
8 Schritte
t=3
Setze Markierungen und an Position 0.
In jedem simulierten Schritt:
• Verschiebe um 1 nach rechts.
• Verschiebe um 1 nach links.
Kostet 4j Schritte für die Simulation des j-ten
Schritts.
Insgesamt
Schritte.
12 Schritte
211
Simulation von M
212
Realisierung der Markierungen
Verwende weitere Markierung K, um Kopfpos.
von M zu merken.
Speichere den Zustand q von M.
Wenn K gefunden: δ(q,a) berechnen und
speichern.
• Kopfbewegung 0: K nicht verändern.
• Kopfbewegung 1 und Durchlauf nach rechts:
K im nächsten Schritt schreiben.
• Kopfbewegung 1 und Durchlauf nach links:
K beim Rücklauf des Kopfes schreiben.
213
Vergrößerung des Bandalphabets.
Sei Γ das Bandalphabet der zu sim. TM.
Neues Bandalphabet:
Γ´ = Γ × { ,B} × { ,B} × {K,B}
214
Der Satz von Cook [K5.4]
Nutzen
Satz K5.4.3: SAT ist NP-vollständig.
Weitere NP-Vollständigkeitsbeweise werden
einfacher.
Zur Erinnerung:
Definition von SAT
Eingabe: Formel F in konjunktiver Form.
Frage: Gibt es eine Belegung x der
Variablen, so dass F (x)=1?
Lemma: Sei A NP-vollständig, ApB und
B∈NP. Dann ist auch B NP-vollständig.
Beweis:
∀L∈NP: LpA p B
Aufwändiger Beweis.
215
SAT ist NP-vollständig
Trans. von p: ∀L∈NP: LpB
⇒B NP-vollständig
B∈NP
216
SAT ist NP-vollständig
2. ∀L∈NP: LpSAT:
1. SAT∈NP:
- Variablenbelegung auswürfeln.
- Teste, ob geg. Formel erfüllt.
Sei L∈NP gegeben.
Wir wissen nur: Für L gibt es eine TM, die
• p(n) zeitbeschränkt ist,
• stereotyp ist,
• nichtdeterministisch mit Zufallsbits
Z(1),...,Z(p(n)) arbeitet.
217
218
Reduktion mit verb. Komponenten
Codierung
Sei Q={q0,...,qk–1} u. Γ={a1,...,am} mit am=B.
Idee:
• Für jeden Zeitpunkt t∈{0,...,p(n)}
- den Zustand der TM,
- den Bandinhalt und
- das verwendetes Zufallsbit
durch boolesche Variablen codieren.
• Klauseln konstruieren, die nur dann erfüllt
sind, wenn
- alle Rechenschritte korrekt sind
- am Ende akzeptiert wird.
Variablen Q(i,t) mit 0ik–1 und 0tp(n).
Q(i,t)=1 ⇔ Zustand nach t-ten Schritt ist qi.
Variablen S(i,t) mit 1im und 1tp(n).
S(i,t)=1 ⇔ Im t-ten Schritt wird ai gelesen.
Variablen Z(t) mit 1tp(n).
Im t-ten Schritt wird Zufallsbit Z(t) verwendet.
219
220
Bedingungen an akzept. Rechnung
Letzte Konfiguration akzeptierend
1. Letzte Konfiguration ist akzeptierend.
2. Variablen stellen Konfigurationen dar.
3. Beschreibung für Zeitpunkt t ergibt sich
durch Anwendung der Übergangsfunktion
aus Beschreibung für Zeitpunkt t–1.
4. Variablen für t=0 repräsentieren
Anfangskonfiguration.
Klausel:
221
Hierbei nutzen wir aus, dass die TM in
akzeptierenden Zuständen endlos
weiterrechnet.
222
Variablen codieren Konfigurationen
Codierung d. Bed. „genau eine 1“
Zu jedem Zeitpunkt muss gelten:
• TM ist in genau einem Zustand.
→Für jedes t∈{0,…,p(n)} gibt es genau ein i
mit Q(i,t)=1.
• TM liest genau ein Zeichen.
→Für jedes t∈{1,…,p(n)} gibt es genau ein i
mit S(i,t)=1.
Variablen Y1,...,Yn:
• Klausel, die sicherstellt, dass nicht alle
Variablen gleich 0 sind:
Y1∨...∨Yn
• Klauseln, die sicherstellen, dass höchstens
eine Variable gleich 1 ist.
Für jedes {i,j}: Yi∨Yj
→ Insgesamt O(n2) Klauseln.
223
Variablen codieren Konfigurationen
Zu jedem Zeitpunkt muss gelten:
• TM ist in genau einem Zustand.
→Für jedes t∈{0,…,p(n)} gibt es genau ein i
mit Q(i,t)=1.
• TM liest genau ein Zeichen.
→Für jedes t∈{1,…,p(n)} gibt es genau ein i
mit S(i,t)=1.
⇒ Für jedes t genügen O(|Q|2) bzw. O(m2)
Klauseln (von Eingabelänge unabh.)
⇒ Insgesamt O(p(n)) Klauseln.
225
224
Variablen cod. korrekte Rechnung
• Zustand nach dem t-ten Rechenschritt und
das geschriebene Zeichen hängen ab von
– Zustand nach d. (t–1)-ten Rechenschritt,
also von Q(0,t–1),...,Q(k–1,t–1),
– dem t-ten Zufallsbit, also von Z(t),
– gelesenen Zeichen, also von
S(1,t),...,S(m,t),
• sind also Funktionen in k+m+1 Variablen.
• haben KNF mit 2k+m+1=O(1) Klauseln.
226
Welche Var. müssen korrekt sein?
Codierung d.Anfangskonfiguration
Sei N(t) der erste Zeitpunkt nach t, wo auf die
TM auf dieselbe Bandzelle wie in Schritt t
zugreift.
• Zustand nach dem t-ten Schritt:
Q(0,t),...,Q(k–1,t).
• Geschriebener Bandinhalt:
S(1,N(t)),...,S(m,N(t)) (falls N(t)p(n)).
• Zustand ist q0:
Q(0,0)=1, Q(i,0)=0 für alle i≠0.
Jede dieser Variablen kann durch KNF mit
O(1) Klauseln dargestellt werden.
• Auf dem Band steht an Positionen 0,...,n–1
die Eingabe x0,...,xn–1 (und sonst B=am).
t(j): erster Zeitpunkt, wo Pos. j gelesen wird.
Für j∈{0,...,n–1} und xj=ai :
S(i,t(j))=1.
Für j∈{–p(n),..., –1,n,...,p(n)}: S(m,t(j))=1.
Alle diese Var. wie angegeben konstantsetzen.
227
Zusammenfassung
228
Korrektheit
• Insgesamt O(p(n)) Klauseln.
• Können in polyn. Zeit berechnet werden:
– Simuliere die Kopfbewegungen der
stereotypen TM, um t(j) und N(t) zu
berechnen.
– Dann können die Klauseln wie angegeben
berechnet werden.
229
1. Sei x∈L.
Dann gibt es eine akzeptierende Rechnung
der TM und somit eine Variablenbelegung,
die diese codiert.
Diese erfüllt alle Klauseln.
2. Sei eine erfüllende Belegung der Klauseln
bei Eingabe x gegeben.
Dann gibt es eine akzeptierende Rechnung
für x und somit ist x∈L.
Also haben wir LpSAT bewiesen.
230
Fazit
Bew. d. NP-Vollst. f. neue Probleme
Der Beweis war zwar lang und kompliziert. Die
Leserin und der Leser sollten aber noch einmal
die Beweisidee herausarbeiten und erst
zufrieden sein, wenn sie mit mir der Meinung
sind, dass die Beweisidee und der
Beweisgang einfach sind.
(Ingo Wegener, S. T51)
Sei ein neues Problem X gegeben.
Rezept:
1. Zeige X∈NP ist (meist einfach).
2. Suche ein geeignetes NP-vollständiges
Problem L für die Reduktion.
Literaturtipp: M.R. Garey, D.S. Johnson:
Computers and Intractability, A Guide to
the Theory of NP-Completeness, 1979.
Anhang mit ca. 500 NP-vollst. Problemen
231
Fortsetzung des Rezepts
232
Zusammenfassung
3. Entwirf eine polyn. berechenbare Funktion f.
4. Beweise, dass f die Red. LpX realisiert:
– x∈L ⇒ f(x)∈X.
– x∉L ⇒ f(x)∉X.
Wenn man keine Reduktion findet:
... vielleicht gibt es einen polyn. Algo für X.
... vielleicht findet man eine Idee für einen
solchen Algo, wenn man erkennt, woran die
Reduktion scheitert.
233
• Wenn ein NP-vollständiges Problem einen
polyn. Algo hat, haben alle NP-vollständigen
Probleme polyn. Algos und es ist P=NP.
• Wenn man beweisen kann, dass ein NPvollständiges Problem keinen polyn. Algo
hat, gilt dies für alle NP-vollst. Probleme und
es ist P≠NP.
• Es gibt viele praktisch wichtige NP-vollst.
Probleme.
• Da man für keines einen polyn. Algo kennt,
wird vermutet, dass P≠NP ist.
234
NP-vollst. u. NP-äquiv. Probleme
Bisher bewiesen (vgl. Folie 189)
Literatur: Kapitel K6.
Ziel:
• Weitere Probleme kennen lernen
(und damit weitere Basisprobleme für eigene
Reduktionen)
• Weitere Beispiele für
NP-Vollständigkeitsbeweise kennen lernen.
Partition p BP
SAT =p 3-SAT
p IS =p Clique =p VC
p
DHC =p HC =p TSP2,∆,sym
NP-vollständig
2-SAT∈P (Übungen)
235
236
Folgerung
Rucksackprobleme [K6.3]
Die Optimierungsvarianten von IS, Clique, VC
und TSP sind NP-äquivalent.
Subset Sum Problem (SSS)
Eingabe: Zahlen a1,...,an, G.
Frage: Gibt es eine Menge I⊆{1,...,n}, so
dass ∑i∈I=G?
Satz K6.3.1: SSS ist NP-vollständig.
Beweis: 1. SSS∈NP.
2. Reduktion von 3-SAT.
237
Reduktion mit
verbundenen
Komponenten
238
Für jede Variable xi:
3. Angabe der Funktion f.
Eingabe für 3-SAT: Variablen x1,...,xn,
Klauseln C1,...,Cm.
Zahlen der SSS-Eingabe:
- n+m Ziffern in Dezimaldarstellung.
- Für jede Variable xi zwei Zahlen ai und bi:
C1 C2
ai
bi
... Cm x1 x2
0 0
0 0
... Cj
1
1
...
0
0
ai
bi
xi
1
1
... xn
0 0
0 0
falls Cj xi enthält
239
b1
a2
a3
a4
d1
e1
e2
C2
1
C3
1
C4
x1
1
1
1
1
2
3
x3
x4
1
1
1
x2
1
1
1
1
2
1
1
1
1
1
1
1
1
1
1
1
d4
1
3
3
3
3
C1 = x1 ∨ x2 ∨ x3, C2 = x1 ∨ x2 ∨ x4,
C3 = x1 ∨ x3 ∨ x4, C4 = x2 ∨ x3 ∨ x4.
... Cj
1
1
... Cm x1 x2
0 0
0 0
...
0
0
Für jede Klausel Cj:
falls Cj xi enthält
C1
C1 C2
241
dj
ej
C1 C2
... Cj
... Cm x1 x2
...
xi
... xn
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
... Cm x1 x2
3 3 1 1
...
1
xi
... xn
1 1
Summe G:
G
1
1
... xn
0 0
0 0
xi
C1 C2
3 3
... Cj
3 3
1
240