z. B. BCH-Codes oder Reed-Solomon

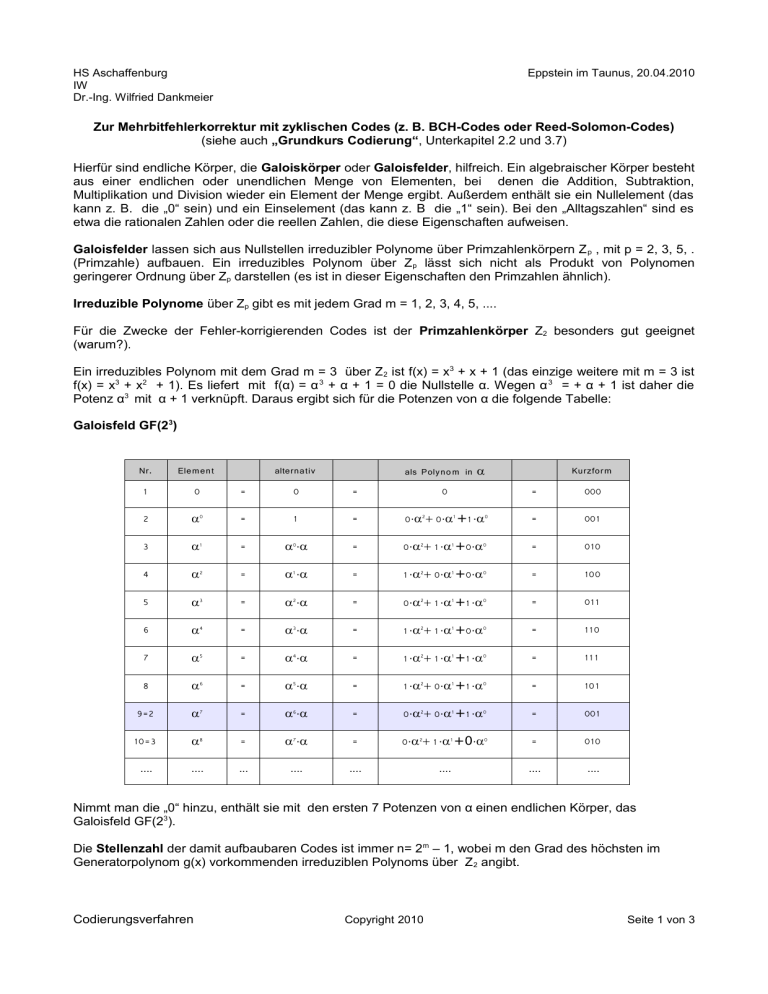
HS Aschaffenburg
IW
Dr.-Ing. Wilfried Dankmeier
Eppstein im Taunus, 20.04.2010
Zur Mehrbitfehlerkorrektur mit zyklischen Codes (z. B. BCH-Codes oder Reed-Solomon-Codes)
(siehe auch „Grundkurs Codierung“, Unterkapitel 2.2 und 3.7)
Hierfür sind endliche Körper, die Galoiskörper oder Galoisfelder, hilfreich. Ein algebraischer Körper besteht
aus einer endlichen oder unendlichen Menge von Elementen, bei denen die Addition, Subtraktion,
Multiplikation und Division wieder ein Element der Menge ergibt. Außerdem enthält sie ein Nullelement (das
kann z. B. die „0“ sein) und ein Einselement (das kann z. B die „1“ sein). Bei den „Alltagszahlen“ sind es
etwa die rationalen Zahlen oder die reellen Zahlen, die diese Eigenschaften aufweisen.
Galoisfelder lassen sich aus Nullstellen irreduzibler Polynome über Primzahlenkörpern Z p , mit p = 2, 3, 5, .
(Primzahle) aufbauen. Ein irreduzibles Polynom über Z p lässt sich nicht als Produkt von Polynomen
geringerer Ordnung über Zp darstellen (es ist in dieser Eigenschaften den Primzahlen ähnlich).
Irreduzible Polynome über Zp gibt es mit jedem Grad m = 1, 2, 3, 4, 5, ....
Für die Zwecke der Fehler-korrigierenden Codes ist der Primzahlenkörper Z2 besonders gut geeignet
(warum?).
Ein irreduzibles Polynom mit dem Grad m = 3 über Z 2 ist f(x) = x3 + x + 1 (das einzige weitere mit m = 3 ist
f(x) = x3 + x2 + 1). Es liefert mit f(α) = α 3 + α + 1 = 0 die Nullstelle α. Wegen α 3 = + α + 1 ist daher die
Potenz α3 mit α + 1 verknüpft. Daraus ergibt sich für die Potenzen von α die folgende Tabelle:
Galoisfeld GF(23)
als Polynom in α
Nr.
Element
alternativ
Kurzform
1
0
=
0
=
0
=
000
2
α0
=
1
=
0⋅α2 + 0⋅α1 +1 ⋅α0
=
001
3
α1
=
α0⋅α
=
0⋅α2+ 1 ⋅α1 +0⋅α0
=
010
4
α2
=
α1 ⋅α
=
1 ⋅α2+ 0⋅α1 +0⋅α0
=
100
5
α3
=
α2⋅α
=
0⋅α2+ 1 ⋅α1 +1 ⋅α0
=
011
6
α4
=
α3⋅α
=
1 ⋅α2+ 1 ⋅α1 +0⋅α0
=
110
7
α5
=
α4⋅α
=
1 ⋅α2+ 1 ⋅α1 +1 ⋅α0
=
11 1
8
α6
=
α5⋅α
=
1 ⋅α2+ 0⋅α1 +1 ⋅α0
=
101
9=2
α7
=
α6⋅α
=
0⋅α2+ 0⋅α1 +1 ⋅α0
=
001
10=3
α8
=
α7⋅α
=
0⋅α2+ 1 ⋅α1 +0⋅α0
=
010
....
....
...
....
....
....
....
....
Nimmt man die „0“ hinzu, enthält sie mit den ersten 7 Potenzen von α einen endlichen Körper, das
Galoisfeld GF(23).
Die Stellenzahl der damit aufbaubaren Codes ist immer n= 2m – 1, wobei m den Grad des höchsten im
Generatorpolynom g(x) vorkommenden irreduziblen Polynoms über Z 2 angibt.
Codierungsverfahren
Copyright 2010
Seite 1 von 3
HS Aschaffenburg
IW
Dr.-Ing. Wilfried Dankmeier
Eppstein im Taunus, 20.04.2010
Hier einige Polynome über Z2 für die Grade m = 1, 2 , 3, 4:
m
m
m
m
=
=
=
=
1:
2:
3:
4:
x 1 1
x 2 x 1 1
x 3 x 1 1 u n d x 3 x 2 1
x 4 x 1 1 u n d x 4 x 3 x 2 x 1 1
Ein Galoisfeld GF(24) kann über
u n d x 4 x 3 1
das definierende Polynom f(x) = x4 + x + 1 für das Element β wie
folgt aufgebaut werden:
als Polynom in β
Nr.
Element
alternativ
Kurzform
1
0
=
0
=
0
=
0000
2
β0
=
1
=
0⋅β3+0⋅β2 + 0⋅β1 +1 ⋅β0
=
0001
3
β1
=
β0⋅β
=
0⋅β3+0⋅β2 +1 ⋅β1 +0⋅β0
=
0010
4
β2
=
β1 ⋅β
=
0⋅β3+1 ⋅β2 + 0⋅β1 +0⋅β0
=
0100
5
β3
=
β2 ⋅β
=
1 ⋅β3+0⋅β2 + 0⋅β1 +0⋅β0
=
1000
6
β4
=
β3 ⋅β
=
0⋅β3+0⋅β2 + 1 ⋅β1 +1 ⋅β0
=
0011
7
β5
=
β4 ⋅β
=
0⋅β3+1 ⋅β2 + 1 ⋅β1 +0⋅β0
=
0110
8
β6
=
β5 ⋅β
=
1 ⋅β3+1 ⋅β2 + 0⋅β1 +0⋅β0
=
1100
9
β7
=
β6 ⋅β
=
1 ⋅β3+0⋅β2 + 1 ⋅β1 +1 ⋅β0
=
101 1
10
β8
=
β7 ⋅β
=
0⋅β3+1 ⋅β2 + 0⋅β1 +1 ⋅β0
=
0101
11
β9
β8 ⋅β
1 ⋅β3+0⋅β2 + 1 ⋅β1 +0⋅β0
1010
12
β10
β9 ⋅β
0⋅β3+1 ⋅β2 + 1 ⋅β1 +1 ⋅β0
011 1
13
β11
β10 ⋅β
1 ⋅β3+1 ⋅β2 + 1 ⋅β1 +0⋅β0
1110
14
β12
β11 ⋅β
1 ⋅β3+1 ⋅β2 + 1 ⋅β1 +1 ⋅β0
111 1
15
β13
β12 ⋅β
1 ⋅β3+1 ⋅β2 + 0⋅β1 +1 ⋅β0
1101
16
β14
β13 ⋅β
1 ⋅β3+0⋅β2 + 0⋅β1 +1 ⋅β0
1001
17
β15
β14 ⋅β
0⋅β3+0⋅β2 + 0⋅β1 +1 ⋅β0
0001
Der damit konstruierbare Code hat die Länge n = 2 4 – 1 = 15. Er ist zur Korrektur von tko = 1, 2, oder 3
Fehlern (Voraussetzung immer: HD-Demodulation. Für Soft-Decision SD kann man bessere = geringere
Restfehlerraten erwarten ).
Aber Vorsicht: Für Codes zur Korrektur von tkor Fehlern sind nur ganz bestimmte Kombinationen
irreduziblen Polynomen geeignet (Begründung siehe „Grundkurs Codierung“, Unterkapitel 3.7).
von
Hier der prinzipielle Weg zur Erzeugung von zyklischen Codewörtern und zur Decodierung der HDCodierungsverfahren
Copyright 2010
Seite 2 von 3
HS Aschaffenburg
IW
Dr.-Ing. Wilfried Dankmeier
Eppstein im Taunus, 20.04.2010
Empfangswörter w(x):
Nullstellen im GF(2 m )
a 1 , a 2, ..... , a t
irreduzible Teilpolynome hierzu
g 1 (a1 )= 0, g 2 (a)= .0, ....., g(t )= 0
Generatorpolynom
g(x) = g 1 (x)·g 2(x)· ...... g t(x)
Infopolynom
u(x)
Codewortpolynom
u(x)·x grad g(x) + [u(x)·xgrad g(x)] MOD g(x)
Fehlerpolynom
e(x)
Empfangswortpolynom
w(x) = v(x) + e(x)
Syndrompolynom
s(x) = w(x) MOD g(x) = e(x) MOD g(x)
Werte von s(x) an den Null stellen:
- für x= a 1
s(a1 )= v(a1 )+ e(a1 )= 0 + e(a1 )= e(a1 )
- für x = a 2
s(a2 )= v(a2)+ e(a2)= 0 + e(a2)= e(a2)
-.........
.........
- für x = a t
s(at )= v(at)+ e(at)= 0 + e(at)= e(at)
Codierungsverfahren
Copyright 2010
Seite 3 von 3