1_3_Kraftwirkungen
Werbung
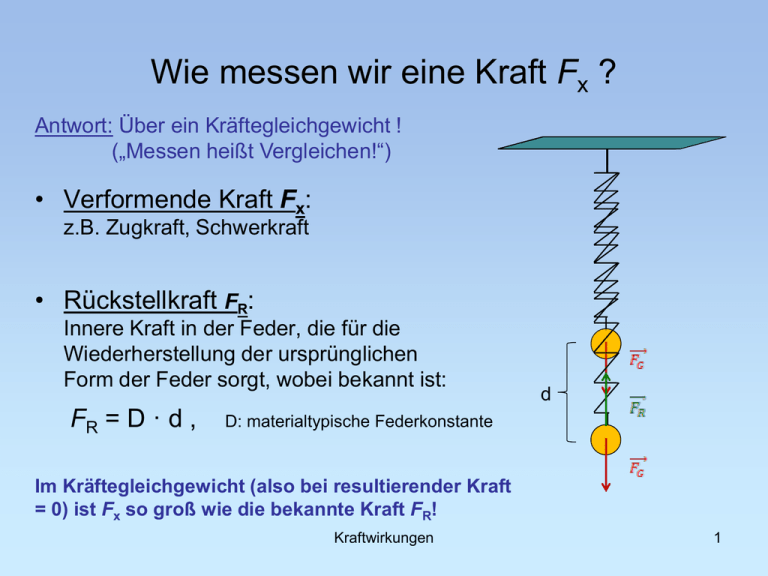
Wie messen wir eine Kraft Fx ? Antwort: Über ein Kräftegleichgewicht ! („Messen heißt Vergleichen!“) • Verformende Kraft Fx: z.B. Zugkraft, Schwerkraft • Rückstellkraft FR: Innere Kraft in der Feder, die für die Wiederherstellung der ursprünglichen Form der Feder sorgt, wobei bekannt ist: FR = D · d , d D: materialtypische Federkonstante Im Kräftegleichgewicht (also bei resultierender Kraft = 0) ist Fx so groß wie die bekannte Kraft FR! Kraftwirkungen 1 Elastische Kräfte Statischer Fall: Kräftegleichgewicht: Hooke‘sches Gesetz Dynamischer Fall: Zusätzliche verformende Kraft fällt nach kurzer Zeit wieder weg, rücktreibende Kraft und Gewichtskraft überwiegen abwechselnd: Schwingung um die Gleichgewichtslage im elastischen Fall: harmonische Schwingung: y ( t ) y 0 sin( t ) mit v ( t ) y 0 cos( t ) 2 ,y 1 0 T d d 2 y a ( t ) y 0 ² sin( t ) Kraftwirkungen 2 Reibungskräfte Ursache: Oberflächenrauhigkeit Kleine Unebenheiten der Oberflächen verhaken sich und hemmen so die Verschiebung. Die Schwerkraft/Gewichtskraft FG drückt den Gegenstand in die Unterlage. Genauer: Die Kraft, die senkrecht auf die Unterlage wirkt (Auflagekraft FN ) Starke Vergrößerung Verzahnung der Oberflächen bei der Reibung FR Die Reibung wird gekennzeichnet durch den Reibungskoeffizienten FR FN Kraftwirkungen 3 Reibungskräfte Wechselwirkung zwischen den Oberflächen eines (ruhenden oder bewegten) Gegenstandes und seines Untergrundes. Haftreibung: Bewegung wird verhindert Gleitreibung und Rollreibung: Bewegung wird durch eine konstante Kraft gebremst. Kraftwirkungen 4 Reibungskräfte Die Gleitreibungskraft ist kleiner als die Haftreibungskraft ! Kräfte bei der Rotation Kräftefreie Bewegung: geradlinig, gleichförmig Drehbewegung: Fortlaufende Richtungsänderung aufgrund einer wirkenden Kraft. Bei einer Bewegung mit konstanter Geschwindigkeit wirkt eine konstante Zentralkraft. Richtungsänderung auf den Mittelpunkt der Kreisbahn hin: Zentripetalkraft Beispiel: Schleuderversuch Kraftwirkungen 6 Kräfte bei der Rotation • Beschreibung der Drehbewegung über die Winkeländerung: a t s „Winkelgeschwindigkeit” a r • Geschwindigkeit einer Masse ist tangential zur Kreisbahn gerichtet: v t (Bahngeschwindigkeit) Wie bestimme ich v t ? a 2 s 2 r pro Zeit: a t s r t Kraftwirkungen vt r vt r 7 Kräfte bei der Rotation • Die Beschleunigung (und damit die Kraft) der rotierenden Masse besitzt sowohl eine tangentiale at vt / t als auch radiale Komponente a r . Wie bestimme ich a r ? Die Bahngeschwindigkeiten in Abb. a) zu den jeweiligen Zeitpunkten 1, 2, 3 und 4 sind in Abb. b) von einem gemeinsamen Punkt M aus aufgetragen. Kraftwirkungen 8 Kräfte bei der Rotation Die Zusatzgeschwindigkeit v a t in je einem Zeitintervall verbindet benachbarte Pfeilspitzen. Für eine Beschleunigung gilt immer: a Dreiecke (0,1,2). und (M,v1,v2) auch v vt s r a vt r s t s t v t , und wegen der Ähnlichkeit der Für t 0 : a r lim a v t r 2 t 0 Jetzt steht a r senkrecht auf v t ! (Zentripetalbeschleunigung) F m ar m r 2 (Zentripetalkraft) 9 Planetenbahnen Zentripetalkraft: Gravitation FG Γ m Planet M Sonne r² Kepler´sche Gesetze: 1. Die Umlaufbahnen aller Planeten haben die Form von einer Ellipse, wobei die Sonne in einem ihrer Brennpunkte steht. Δt2 2. Die Verbindungslinie von der Sonne zu einem Planeten (Fahrstrahl) überstreicht in gleichen Zeitintervallen gleiche Flächen. (Δt1 = Δt2; A1 = A2) A2 A1 3. m P lanet r 2 r 3 T 2 m P lanet M Sonne r Δt1 2 2 M Sonne const. 10 Gezeiten Ebbe FZF SPErde SPErde-Mond Flut FG Mond Flut Innerhalb von 24 h: 2 x Ebbe 2 x Flut Ebbe Kraftwirkungen 11 Gezeiten Erde R X R Schwerpunkt Mond Für Punkte A, B, C, D auf Erdoberfläche gilt: Fg nimmt mit der Entfernung vom Mond ab. FZ aber ist konstant, da jeder Punkt auf einer Kreisbahn mit gleichem Radius liegt (R = Erdmittel- zu Schwerpunkt). 12 Scheinkräfte Betrachtet man die Bewegung eines Massenpunktes in einem rotierenden Bezugssystem, kann ein außenstehender Beobachter Scheinkräfte sofort aufklären. Ein Beteiligter (mitrotierender Beobachter) sucht vergebens nach dem Wechselwirkungspartner!!! Scheinkräfte: - Zentrifugalkraft - Corioliskraft Zentrifugalkraft: Die Zentrifugalkraft wirkt immer in rotierenden Bezugssystemen: Ein mitbewegter Beobachter fühlt sich aus der Kreisbewegung hinaus gedrückt (Trägheitseffekt) Kraftwirkungen 13 Scheinkräfte Corioliskraft: Die Corioliskraft wirkt nur bei bestimmten Relativbewegungen in einem rotierenden Bezugssystem: Durch die Rotation der Erde entstehen aufgrund der Corioliskraft verschiedene Wetterphänomene: • Durch die Drehbewegung in den Südwind bzw. Nordwind hinein, entsteht der Eindruck des Südost- bzw. Nordost-Passats 30° Nord 30° Süd • Tiefdruckgebiete drehen sich auf der Nordhalbkugel gegen den Uhrzeigersinn und auf der Südhalbkugel im Uhrzeigersinn. (Hochdruckgebiete drehen sich genau anders herum.) Kraftwirkungen 14