Vorlesung 6b

Vorlesung 6b
1
Vorlesung 6b
Von der Binomial-zur
Normalverteilung
Binomialverteilungen mit großem n und großer Varianz npq
sehen “glockenförmig” aus,
wenn man sie geeignet “ins Bild holt”.
2
Binomialverteilungen mit großem n und großer Varianz npq
sehen “glockenförmig” aus,
wenn man sie geeignet “ins Bild holt”.
0.03
0.000
0.010
0.020
n = 1000, p = 0.3
0
200
400
600
800
1000
0.030
n = 1000, p = 0.3
0.000
0.010
0.020
270 ≤ k ≤ 330
270
280
290
300
310
320
330
0.000
0.004
0.008
0.012
n = 4000, p = 0.3
0
1000
2000
3000
4000
0.01
n = 4000, p = 0.3
0.000
0.005
0.010
1140 ≤ k ≤ 1260
1140
1160
1180
1200
1220
1240
1260
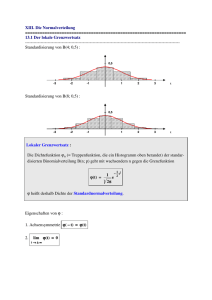
Bezeichne
7
Bezeichne
1 −x2/2
ϕ(x) := √ e
2π
Bezeichne
1 −x2/2
ϕ(x) := √ e
2π
die Dichte der Standard-Normalverteilung.
Bezeichne
1 −x2/2
ϕ(x) := √ e
2π
die Dichte der Standard-Normalverteilung.
Warum und in welchem Sinn lassen sich Binomialgewichte
Bezeichne
1 −x2/2
ϕ(x) := √ e
2π
die Dichte der Standard-Normalverteilung.
Warum und in welchem Sinn lassen sich Binomialgewichte
durch die Normaldichte annähern?
Für n ∈ N und p ∈ (0, 1) sei
8
Für n ∈ N und p ∈ (0, 1) sei
µ := np,
σ :=
√
npq.
Für n ∈ N und p ∈ (0, 1) sei
µ := np,
σ :=
√
npq.
Für die Binomialgewichte schreiben wir kurz
Für n ∈ N und p ∈ (0, 1) sei
µ := np,
σ :=
√
npq.
Für die Binomialgewichte schreiben wir kurz
n k n−k
p q
.
w(k) :=
k
Es stellt sich heraus (eine Heuristik dafür folgt gleich):
9
Es stellt sich heraus (eine Heuristik dafür folgt gleich):
Für großes σ
Es stellt sich heraus (eine Heuristik dafür folgt gleich):
Für großes σ
und k nicht allzu weit vom Zentrum np ist
Es stellt sich heraus (eine Heuristik dafür folgt gleich):
Für großes σ
und k nicht allzu weit vom Zentrum np ist
1 k − µ
w(k) ≈ ϕ
σ
σ
Es stellt sich heraus (eine Heuristik dafür folgt gleich):
Für großes σ
und k nicht allzu weit vom Zentrum np ist
1 k − µ
w(k) ≈ ϕ
σ
σ
Zur Erinnerung:
Es stellt sich heraus (eine Heuristik dafür folgt gleich):
Für großes σ
und k nicht allzu weit vom Zentrum np ist
1 k − µ
w(k) ≈ ϕ
σ
σ
Zur Erinnerung:
1 x − µ
ϕ
dx
σ
σ
Es stellt sich heraus (eine Heuristik dafür folgt gleich):
Für großes σ
und k nicht allzu weit vom Zentrum np ist
1 k − µ
w(k) ≈ ϕ
σ
σ
Zur Erinnerung:
1 x − µ
ϕ
dx
σ
σ
ist die Dichte der Normalverteilung
mit Erwartungswert µ und Varianz σ 2.
1 k − µ
w(k) ≈ ϕ
σ
σ
10
1 k − µ
w(k) ≈ ϕ
σ
σ
k−µ
Mit zk :=
wird dies zu:
σ
1 k − µ
w(k) ≈ ϕ
σ
σ
k−µ
Mit zk :=
wird dies zu:
σ
w(k) ≈ (zk − zk−1)ϕ(zk ).
Daraus bekommt man für Binom(n, p)-verteiltes K
√
mit großem σ = npq:
11
Daraus bekommt man für Binom(n, p)-verteiltes K
√
mit großem σ = npq:
K−µ
≤ b}
P{a ≤
σ
Daraus bekommt man für Binom(n, p)-verteiltes K
√
mit großem σ = npq:
K−µ
≤ b}
P{a ≤
σ
=
X
k:a≤zk ≤b
w(k)
Daraus bekommt man für Binom(n, p)-verteiltes K
√
mit großem σ = npq:
K−µ
≤ b}
P{a ≤
σ
X
=
w(k)
k:a≤zk ≤b
≈
X
(zk − zk−1)ϕ(zk )
k:a≤zk ≤b
Daraus bekommt man für Binom(n, p)-verteiltes K
√
mit großem σ = npq:
K−µ
≤ b}
P{a ≤
σ
X
=
w(k)
k:a≤zk ≤b
≈
X
(zk − zk−1)ϕ(zk )
k:a≤zk ≤b
≈
Z b
a
ϕ(z) dz.
Fazit:
12
Fazit:
√
Für großes σ = npq ist die Standardisierung
einer binomialverteilten Zufallsvariablen K,
Fazit:
√
Für großes σ = npq ist die Standardisierung
einer binomialverteilten Zufallsvariablen K,
K − np
K −µ
= √
,
σ
npq
Fazit:
√
Für großes σ = npq ist die Standardisierung
einer binomialverteilten Zufallsvariablen K,
K − np
K −µ
= √
,
σ
npq
approximativ so verteilt
wie eine standardnormalverteilte Zufallsvariable Z:
Fazit:
√
Für großes σ = npq ist die Standardisierung
einer binomialverteilten Zufallsvariablen K,
K − np
K −µ
= √
,
σ
npq
approximativ so verteilt
wie eine standardnormalverteilte Zufallsvariable Z:
K−µ
∈ [a, b] ≈ P{Z ∈ [a, b]}.
P
σ
Abraham de Moivre
1667-1754
13
Jetzt die versprochene Heuristik für
14
Jetzt die versprochene Heuristik für
1 k − µ
n k n−k
p q
≈ ϕ
w(k) =
:
k
σ
σ
Jetzt die versprochene Heuristik für
1 k − µ
n k n−k
p q
≈ ϕ
w(k) =
:
k
σ
σ
Idee: Betrachte die “sukzessiven Quotienten”
Jetzt die versprochene Heuristik für
1 k − µ
n k n−k
p q
≈ ϕ
w(k) =
:
k
σ
σ
Idee: Betrachte die “sukzessiven Quotienten”
n−k+1 p
w(k)
=
,
w(k − 1)
k
q
Jetzt die versprochene Heuristik für
1 k − µ
n k n−k
p q
≈ ϕ
w(k) =
:
k
σ
σ
Idee: Betrachte die “sukzessiven Quotienten”
n−k+1 p
w(k)
=
,
w(k − 1)
k
q
aufmultipliziert beginnend vom “Zentrum”
Jetzt die versprochene Heuristik für
1 k − µ
n k n−k
p q
≈ ϕ
w(k) =
:
k
σ
σ
Idee: Betrachte die “sukzessiven Quotienten”
n−k+1 p
w(k)
=
,
w(k − 1)
k
q
aufmultipliziert beginnend vom “Zentrum”
ℓ := ⌊(n + 1)p⌋.
Ein paar Zeilen Rechnung (vgl. Skript Wak S. 80) ergeben für
j = 1, 2, , . . . mit j ≪ n:
15
Ein paar Zeilen Rechnung (vgl. Skript Wak S. 80) ergeben für
j = 1, 2, , . . . mit j ≪ n:
j
w(ℓ + j) ≈ − 2.
ln
w(ℓ + j − 1)
σ
Ein paar Zeilen Rechnung (vgl. Skript Wak S. 80) ergeben für
j = 1, 2, , . . . mit j ≪ n:
j
w(ℓ + j) ≈ − 2.
ln
w(ℓ + j − 1)
σ
Aufsummiert zwischen j = 1 und j = k − ℓ :
Ein paar Zeilen Rechnung (vgl. Skript Wak S. 80) ergeben für
j = 1, 2, , . . . mit j ≪ n:
j
w(ℓ + j) ≈ − 2.
ln
w(ℓ + j − 1)
σ
Aufsummiert zwischen j = 1 und j = k − ℓ :
1 (k − ℓ)2
1 k − µ 2
w(k) ln
≈− 2
≈−
w(ℓ)
σ
2
2
σ
Ein paar Zeilen Rechnung (vgl. Skript Wak S. 80) ergeben für
j = 1, 2, , . . . mit j ≪ n:
w(ℓ + j) j
ln
≈ − 2.
w(ℓ + j − 1)
σ
Aufsummiert zwischen j = 1 und j = k − ℓ :
1 (k − ℓ)2
1 k − µ 2
w(k) ≈− 2
≈−
ln
w(ℓ)
σ
2
2
σ
√
1 k − µ
1 k − µ 2
= w(ℓ)σ 2π ϕ
w(k) ≈ w(ℓ) exp −
2
σ
σ
σ
√
1 k − µ
w(k) ≈ w(ℓ) σ 2π ϕ
σ
σ
16
√
1 k − µ
w(k) ≈ w(ℓ) σ 2π ϕ
σ
σ
Summation über k:
√
1 k − µ
w(k) ≈ w(ℓ) σ 2π ϕ
σ
σ
Summation über k:
√
1 ≈ w(ℓ)σ 2π
√
1 k − µ
w(k) ≈ w(ℓ) σ 2π ϕ
σ
σ
Summation über k:
√
1 ≈ w(ℓ)σ 2π
1 k − µ
w(k) ≈ ϕ
σ
σ
√
1 k − µ
w(k) ≈ w(ℓ) σ 2π ϕ
σ
σ
Summation über k:
√
1 ≈ w(ℓ)σ 2π
1 k − µ
w(k) ≈ ϕ
σ
σ
So weit die Heuristik.
Den folgenden “lokalen Grenzwertsatz” bekommt man
mit der (erstmals von de Moivre entdeckten) Stirling-Formel
17
Den folgenden “lokalen Grenzwertsatz” bekommt man
mit der (erstmals von de Moivre entdeckten) Stirling-Formel
(vgl. Skript Wa S. 84-85, auf S. 82 ff findet sich dort
auch ein Beweis der Stirling-Formel).
Satz
18
Satz
Sei p ∈ (0, 1) fest, und kn eine Folge natürlicher Zahlen mit
Satz
Sei p ∈ (0, 1) fest, und kn eine Folge natürlicher Zahlen mit
2
|kn − np|
= 0).
(d.h. n→∞
lim
|kn − np| = o(n 3 )
2
n3
Satz
Sei p ∈ (0, 1) fest, und kn eine Folge natürlicher Zahlen mit
2
|kn − np|
= 0).
(d.h. n→∞
lim
|kn − np| = o(n 3 )
2
n3
Dann gilt für die Binomialgewichte b(n, p; kn) mit n → ∞
2
−np)
1
1
− (kn2npq
√
b(n, p; kn) ∼ √
.
e
npq 2π
Satz
Sei p ∈ (0, 1) fest, und kn eine Folge natürlicher Zahlen mit
2
|kn − np|
3
|kn − np| = o(n )
= 0).
(d.h. n→∞
lim
2
n3
Dann gilt für die Binomialgewichte b(n, p; kn) mit n → ∞
2
−np)
1
1
− (kn2npq
√
.
e
b(n, p; kn) ∼ √
npq 2π
bn ∼ an,
dass die Folge der Quotienten bn/an gegen Eins konvergiert.
Dabei bedeutet
Aus dem lokalen Grenzwertsatz ergibt sich durch Summieren
und Kontrollieren der Fehlerterme (vgl. Skript Wa S. 86) ein
19
Aus dem lokalen Grenzwertsatz ergibt sich durch Summieren
und Kontrollieren der Fehlerterme (vgl. Skript Wa S. 86) ein
1)
Globaler Grenzwertsatz, von de Moivre (1733, für p = 2
und Laplace (1810, für p allgemein))
Aus dem lokalen Grenzwertsatz ergibt sich durch Summieren
und Kontrollieren der Fehlerterme (vgl. Skript Wa S. 86) ein
1)
Globaler Grenzwertsatz, von de Moivre (1733, für p = 2
und Laplace (1810, für p allgemein))
Für n = 1, 2, . . . sei Kn eine binomial(n, p)-verteilte
−np
ihre Standardisierung.
Zufallsvariable, und Kn∗ := K√nnpq
Aus dem lokalen Grenzwertsatz ergibt sich durch Summieren
und Kontrollieren der Fehlerterme (vgl. Skript Wa S. 86) ein
1)
Globaler Grenzwertsatz, von de Moivre (1733, für p = 2
und Laplace (1810, für p allgemein))
Für n = 1, 2, . . . sei Kn eine binomial(n, p)-verteilte
−np
Zufallsvariable, und Kn∗ := K√nnpq
ihre Standardisierung.
Dann gilt für alle a < b ∈ R:
∗
lim
P
({K
n ∈ [a, b]}) =
n→∞
Zb
a
ϕ(z)dz,
1 − z2
mit ϕ(z) = √ e 2 .
2π
Man sagt dafür auch kurz:
20
Man sagt dafür auch kurz:
Die Folge der Zufallsvariablen Kn∗
konvergiert in Verteilung
gegen eine standard-normalverteilte Zufallsvariable Z.