Elektrostatik
Werbung

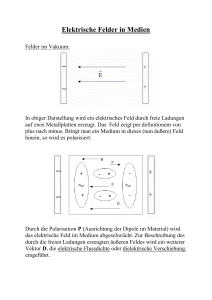
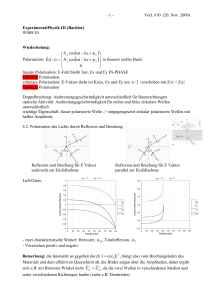
Elektrostatik ~ in Anwesenheit einer Polarisation P~ kann auf verschiedene Arten Das elektrische Feld E berechnet werden. Einerseits kann die Polarisation als Quelle von Polarisationsladungen betrachtet und dann das elektrische Feld wie gewöhnlich aus dieser effektiven Ladungsverteilung berechnet werden. Andererseits kann die Polarisation aber auch selbst als Bestandteil des elektrischen Feldes betrachtet werden. In diesem Fall ist ein Hilfsfeld einzuführen. Rechnen mit effektiven Ladungsdichten In Anwesenheit einer Polarisation P~ (~r ) wird die Elektrostatik durch die beiden folgenden Maxwell-Gleichungen beschrieben: 1 (ρfrei + ρpol ) ε0 ~ = 0 , rotE ~ = divE , wobei ρpol = −divP~ . Die effektive Ladungsdichte ist jetzt ρeff = ρfrei + ρpol . Das elektrische Feld lässt sich damit über Z 1 ~r − ~r ′ ′ ′ ~ E (~r ) = ρeff (~r ) · 3 dV ′ 4π V ′ |~r − ~r | berechnen. Es ergibt sich auch aus dem elektrostatischen Potenzial: Z 1 ρeff (~r ′ ) ~ E = −grad Φe , wobei Φ (~r ) = dV ′ ′ 4πε0 V ′ |~r − ~r | . Rechnen mit Hilfsfeldern ~ ein: Wir führen die so genannte dielektrische Verschiebung D ~ := ε0 E ~ + P~ D . ~ mit Die dielektrische Verschiebung verknüpft das physikalisch messbare elektrische Feld E ~ der Polarisation P : ~ = 1 D ~ − P~ E . ε0 ~ gelten die Gleichungen Für D ~ = ρfrei , divD ~ = rotP~ . rotD 1 ~ nun in ein Gradientenfeld D ~ g und ein Rotationsfeld D ~ r: Wir zerlegen D ~ =D ~g +D ~r D . ~ wie folgt: Mit dieser Zerlegung lautet das elektrische Feld E ~ = 1 D ~g + D ~ r − P~ E ε0 . ~ g und D ~ r erfüllen die Gleichungen Die Felder D ~ g = ρfrei divD ~g = 0 rotD , und ~r = 0 , divD ~ r = rotP~ rotD . ~ g und D ~ r lassen sich als Lösungen direkt berechnen: Die Felder D Z 1 ~r − ~r ′ ~ dV ′ , Dg (~r ) = ρfrei (~r ′ ) · 4π V ′ |~r − ~r ′ |3 Z 1 ~r − ~r ′ ′ ~ r (~r ) = D . rotP~ (~r ′ ) × 3 dV ′ 4π V ′ |~r − ~r | Sie lassen sich aber auch aus Potenzialen bestimmen: ~ g = −grad Φe D ~ r = rot C ~e D , , 1 wobei Φe (~r ) = 4π ρfrei (~r ′ ) dV ′ , ′ |~ r − ~ r | V′ Z rotP~ (~r ′ ) ~ e (~r ) = 1 wobei C dV ′ . 4π V ′ |~r − ~r ′ | Z Zürich, November 2006 Oliver Portmann 2