normalverteilung
Werbung
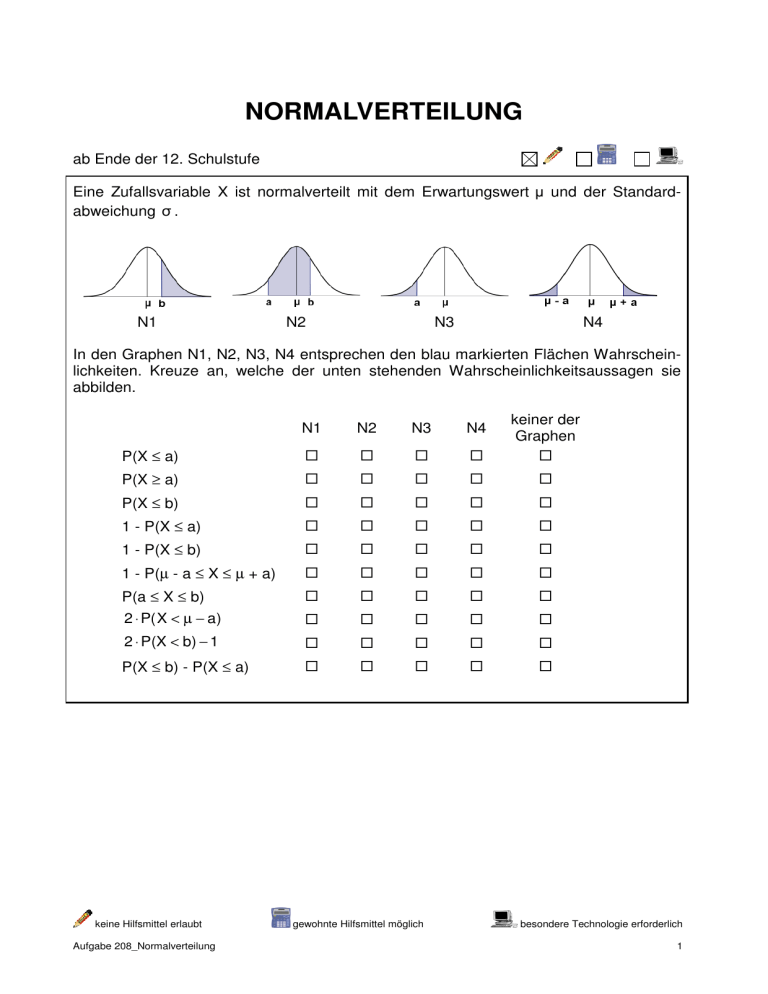
NORMALVERTEILUNG ab Ende der 12. Schulstufe Eine Zufallsvariable X ist normalverteilt mit dem Erwartungswert µ und der Standardabweichung σ . N1 N2 N3 N4 In den Graphen N1, N2, N3, N4 entsprechen den blau markierten Flächen Wahrscheinlichkeiten. Kreuze an, welche der unten stehenden Wahrscheinlichkeitsaussagen sie abbilden. N1 N2 N3 N4 P(X ≤ a) keiner der Graphen P(X ≥ a) P(X ≤ b) 1 - P(X ≤ a) 1 - P(X ≤ b) 1 - P(µ - a ≤ X ≤ µ + a) P(a ≤ X ≤ b) 2 ⋅ P( X < µ − a) 2 ⋅ P(X < b) − 1 P(X ≤ b) - P(X ≤ a) keine Hilfsmittel erlaubt Aufgabe 208_Normalverteilung gewohnte Hilfsmittel möglich besondere Technologie erforderlich 1 Möglicher Lösungsweg N1 N2 N3 N4 P(X ≤ a) keiner der Graphen P(X ≥ a) P(X ≤ b) 1 - P(X ≤ a) 1 - P(X ≤ b) 1 - P(µ - a ≤ X ≤ µ + a) P(a ≤ X ≤ b) 2 ⋅ P( X < µ − a) 2 ⋅ P(X < b) − 1 P(X ≤ b) - P(X ≤ a) Normalverteilung 2 Klassifikation Wesentliche Bereiche der Handlungsdimension H3 • Werte aus Tabellen oder grafischen Darstellungen ablesen, sie im jeweiligen Kontext deuten Wesentliche Bereiche der Inhaltsdimension I4 • stetige Verteilung: Normalverteilung Wesentliche Bereiche der Komplexitätsdimension K3 • Einsetzen von Reflexionswissen, Reflektieren Nachhaltigkeitserwartung N1 • immer verfügbar Technologieeinfluss Für das Lösen dieser Aufgabe ist regelmäßiger Technologieeinsatz im Unterricht erforderlich. vorteilhaft. neutral. Kommentar Online-Vergleichsarbeit September 2009 Normalverteilung 3