Wahrscheinlichkeitsrechnung und Zufallsvariablen

1 Wahrscheinlichkeitsrechnung und Zufallsvariablen
Zoltán Zomotor
Versionsstand: 18. Mai 2015, 09:29
Die nummerierten Felder bitte während der Vorlesung ausfüllen.
This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Germany License.
To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/de/ or send a letter to Creative
Commons, 171 Second Street, Suite 300, San Francisco, California, 94105, USA.
Bitte hier notieren, was beim Bearbeiten unklar geblieben ist:
Inhaltsverzeichnis
1 Einleitung
2
2 Wahrscheinlichkeitsrechnung
2.1 Zufallsvorgänge . . . . . . . . . . .
2.2 Ereignisse und ihre Darstellung . .
2.3 Wahrscheinlichkeit von Ereignissen
2.4 Übungsaufgaben . . . . . . . . . .
3 Zufallsvariablen
3.1 Diskrete Zufallsvariablen
3.2 Stetige Zufallsvariablen
3.2.1 Eigenschaften . .
3.2.2 Beispiel . . . . .
3.3 Übungsaufgaben . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
2
2
3
8
.
.
.
.
.
8
8
10
10
11
11
1 Einleitung
1
1 Einleitung
Dieses und die folgenden Skripte basieren auf dem Foliensatz zum Buch [BBK12] sowie auf
[Pap11]. Für die Vorlesung benötigen Sie nur [Pap11], das Sie als eBook aus dem Netz der
DHBW-Stuttgart kostenlos herunterladen können.
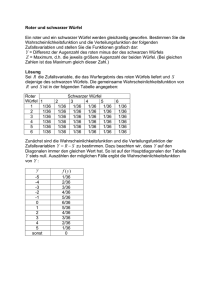
2 Wahrscheinlichkeitsrechnung1
2.1 Zufallsvorgänge
Zufallsvorgang
1
Geschehen mit ungewissem Ausgang, z.B. Münzwurf
Elementarereignis ω
2
3
Ein möglicher Ausgang, z.B. „Kopf“
Elementarereignisse schließen sich gegenseitig aus „Kopf“ XOR „Zahl“
Ergebnismenge Ω
4
Menge aller Elementarereignisse
Ergebnis
5
Tatsächlich eingetretenes Elementarereignis
Beispiel: Werfen zweier Würfel
6
n
Ω = (x1 , x2 ): x1 , x2 ∈ {1, . . . , 6}
o
2.2 Ereignisse und ihre Darstellung
Ereignis A
7
8
1
Folgeerscheinung eines Ergebnisses, A ⊂ Ω
Ereignisse schließen sich nicht gegenseitig aus
[Pap11, Teil II, Kapitel 1 bis 3]
2
2 Wahrscheinlichkeitsrechnung
1
Beispiel: Werfen zweier Würfel
Ereignis
verbal
formal
9
A
Augensumme = 4
10
B
Erste Zahl = 2
{(1, 3), (2, 2), (3, 1)}
{(2, 1), (2, 2), . . . , (2, 6)}
Tabelle 1: Sprech-/Schreibweisen bei Bildung von Ereignissen
Beschreibung des zugrundeliegenden Sachverhalts
Bezeichnung
(Sprechweise)
Darstellung in Ω
(Schreibweise als
Teilmenge)
11
1.
A tritt sicher ein
A ist sicheres Ereignis
12
2.
A tritt sicher nicht ein
A ist unmögliches Ereignis
A=Ω
A=∅
13
3.
wenn A eintritt, tritt B ein
4.
genau dann, wenn A eintritt, A und B sind äquivalente
tritt B ein
Ereignisse
5.
wenn A eintritt, tritt B
nicht ein
A⊂B
A ist Teilereignis von B
14
15
A und B sind disjunkte Ereignisse
A=B
A∩B =∅
16
6.
7.
8.
genau dann, wenn A eintritt,
tritt B nicht ein
genau dann, wenn mindestens ein Aj eintritt (auch: genau
dann, wenn A1 oder A2 oder . . . eintritt),
tritt A ein
genau dann, wenn alle Aj
eintreten (auch: genau dann, wenn
A und B sind komplementäre Ereignisse
A ist Vereinigung der Aj
17
A=
[
Aj
j
A ist Durchschnitt der Aj
18
A=
\
j
A1 und A2 und . . . eintreten)
2.3 Wahrscheinlichkeit von Ereignissen
Wahrscheinlichkeit P (A)
19
B = Ā
Chance für das Eintreten von A
3
Aj
2 Wahrscheinlichkeitsrechnung
1
Axiome der Wahrscheinlichkeitsrechnung
20
1.
21
2.
22
3.
P (A) = 0 für alle A
P (Ω ) = 1
P (A1 ∪ A2 ∪ · · · ) = P (A1 ) + P (A2 ) + · · · , falls alle Aj disjunkt
Laplace-Wahrscheinlichkeit
23
P (A) =
|A|
Anzahl der für A günstigen Fälle
=
|Ω |
Anzahl aller möglichen Fälle
24
Voraussetzung: Alle ω ∈ Ω
gleich wahrscheinlich
Beispiel: Werfen zweier Würfel, Augensumme gleich vier: A = {(1, 3), (2, 2), (3, 1)}
25
|Ω | = 36, |A| = 3 ⇒ P (A) =
3
1
=
= 0.083
36
12
Urnenmodell: Ziehe k Objekte aus einer Menge von n verschiedenen Objekten ([Pap11, Tabelle
1, Seite 264])
ohne
mit
Wiederholung
Wiederholung
26
27
C(n, k) =
Kombinationen
k-ter Ordnung
n
k
!
!
Cw (n, k) =
28
Variationen
k-ter Ordnung
n+k−1
k
ungeordnete
Stichproben
29
Vw (n, k) = nk
n!
V (n, k) =
(n − k)!
geordnete
Stichproben
Ziehung ohne
Zurücklegen
Ziehung mit
Zurücklegen
Beispiel: Parallelschaltung von vier Widerständen, wobei insgesamt 6 verschiedene Widerstände
R1 , R2 , . . . , R6 zur Verfügung stehen. Wie viele verschiedene Schaltmöglichkeiten gibt es,
wenn jeder der 6 Widerstände a) höchstens einmal und b) mehrmals, also bis zu viermal
verwendet werden darf? ([Pap11, Seite 259])
4
2 Wahrscheinlichkeitsrechnung
1
30
Kombination ohne Wiederholung,
n = 6, k = 4
a)
C(6, 4) =
6
4
!
=
6!
= 15
4!2!
31
b)
9 9!
= 126
4 4!5!
!
Kombination mit Wiederholung,
n = 6, k = 4
Cw (6, 4) =
Rechenregeln für Wahrscheinlichkeiten
32
1.
33
2.
34
3.
P (a) 5 1
P (∅) = 0
A ⊂ B ⇒ P (A) 5 P (B)
35
P (Ā) = 1 − P (A)
4.
36
5.
37
P (A ∪ B) = P (A) + P (B) − P (A ∩ B)
P (A ∪ B ∪ C) = P (A) + P (B) + P (C) − P (A ∩ B) − P (A ∩ C) − P (B ∩ C)
+P (A ∩ B ∩ C)
38
6.
P (B) =
X
P (B ∩ Ai ), falls alle Aj disjunkt und
i
[
A3
C
A
Aj = Ω
j
B
A1
A
B
5
A2
2 Wahrscheinlichkeitsrechnung
1
Beispiel: Einmaliges Würfeln
P (A) = P („Augenzahl = 5“)
39
= 1 − P (Ā)
40
= 1 − P („Augenzahl = 6“)
41
= 1 − 1/6 = 5/6
Bedingte Wahrscheinlichkeiten
• Wahrscheinlichkeit B hängt von Ereignis A ab.
42
P (B|A) =
P (B∩A)
P (A)
• Formal:
7. Zufallsvorg
änge, Ereignisse und Wahrscheinlichkeiten
• Im Mengendiagramm:
Baumdiagramm
Beispiel:
Ω
3
5
A
4
6
Urne: 5 rote, 2 schwarze Kugeln;
3-mal Ziehen ohne Zurücklegen
P .r; r; rB
/D
5
7
! 46 ! 35 D
2
7
5
7
2
6
P . 2"r , 1"s“/ D P .r; r; s/ C P .r; s; r / C P .s; r; r /
43 ”
44
Kreis
5 4 2
5 2 4
D 7 ! 6 ! 5 C 7 ! 6 ! 5 CP27(B|A)
! 65 ! 45 = Halbkreis
P (B) =
$
Quadrat
D
4
7
r
2
5
4
5
r
B
1
5
4
5
5
6
2
7
Generell:
Baumdiagramm
s
$
A
P .BjA/
B
P .B \ A/ D P .BjA/ ! P .A/
1
6
r
s
r
r
45
P .A/
s
s
Dreieck
# 0;571
r
1
5
s
1
r
0
s
s
65 j 223
Bamberg et al.: Statistik
6
2 Wahrscheinlichkeitsrechnung
1
hkeiten
7. Zufallsvorgänge, Ereignisse und Wahrscheinlichkeiten
Beispiel: Urnenmodell, 5 rote, 2 schwarze Kugeln, 3-mal Ziehen ohne Zurücklegen.
3
5
2
5
4
5
r
2
7
5
7
C P .r; s; r / C P .s; r; r /
! 26 ! 45 C 27 ! 65 ! 45
jA/
2
6
s
Urne: 5 rote, 2 schwarze Kugeln;
3-mal Ziehen ohne Zurücklegen
P .r; r; r / D
s
$
s
s
1
6
r
D
1
5
s
! 46 ! 35 D
2
7
1
r
Generell:
0
s
$
4
7
# 0;571
P .A/
A
P .BjA/
B
P .B \ A/ D P .BjA/ ! P .A/
65 j 223
Totale Wahrscheinlichkeit: Unbedingte aus bedingten Wahrscheinlichkeiten erschließen. Aus
Bamberg et al.: Statistik
Lücke 38 und 42 folgt:
47
P (B) =
X
P (B ∩ Ai ) =
X
P (B|Ai ) · P (Ai )
i
i
Formel von Bayes: Umkehren von Argument und Bedingung.
48
P (Aj ∩ B) = P (B ∩ Aj )
Lücke 42: ⇒
Lücke 47 ⇒
5
7
$
2
7
s
P .A/
5
7
P . 2"r , 1"s“/ D P .r; r; s/ C P .r; s; r / C P .s; r; r /
”
D 75 ! 46 ! 25 C 75 ! 26 ! 45 C 27 ! 65 ! 45
r
5
6
B
Beispiel:
r
1
5
4
5
2
7
r
r
4
6
ugeln;
klegen
5
7
Baumdiagramm
46
P (Aj |B) · P (B) = P (B|Aj ) · P (Aj )
P (B|Aj ) · P (Aj )
P (Aj |B) = P
P (B|Ai ) · P (Ai )
i
Unabhängigkeit von Ereignissen: A, B unabhängig: Das Eintreten von A ist nicht informativ
bezüglich P (B) und umgekehrt.
49
• Formal: P (B|A) = P (B)
50
• Äquivalent zu: P (B ∩ A) = P (B) · P (A)
7
3 Zufallsvariablen
1
51
• Dann gilt: P (A ∪ B) = P (A) + P (B) − P (A) · P (B)
• Beispiel: Zwei Würfel unabhängig werfen.
A : „erster Würfel gleich 6“
B : „zweiter Würfel gleich 6“
)
52
1 1 1 1
11
⇒ P (A ∪ B) = 6 + 6 − 6 · 6 = 36
2.4 Übungsaufgaben
[Pap11, Teil II, Zu Abschnitt 1 bis 3, Seite 451ff]
3 Zufallsvariablen2
• Beschreibung von Ereignissen durch reelle Zahlen.
53
Formal: Ergebnismenge Ω → R, d.h. ω ∈ Ω → X(ω)
• Vor Durchführung des Zufallsvorgangs:
54
X
Zufallsvariable oder Wertebereich:
• Nach Durchführung des Zufallsvorgangs:
55
Wert oder Realisation:
x
• Beispiel: Würfeln mit Farbwürfel mit der Ergebnismenge
Ω = {blau, grün, lila, rot, schwarz, weiß}
Wir ordnen jeder Farbe eine (sinnvolle) reelle Zahl zu, zum Beispiel b = 0, g = 1, . . .
56
somit ist der Wertebereich =
{0, 1, 2, 3, 4, 5}
57
1
P (X = 0) = ,
6
4
2
=
6
3
P (X 5 3) =
3.1 Diskrete Zufallsvariablen
58
• X heißt diskret, falls ihr Wertebereich
2
endlich
[Pap11, Teil II, Kapitel 4]
8
ist.
3 Zufallsvariablen
1
59
• Dann ist P (X = x) nicht
konstant 0
• Die Funktion
60
f (x) = P (X = x)
61
heißt Wahrscheinlichkeitsfunktion oder
einfache
Wahrscheinlichkeit.
• Für die Verteilungsfunktion gilt dann:
62
F (x) =
P (X 5 x) =
X
f (xi )
xi 5x
63
Die Verteilungsfunktion heißt daher auch
kumulierte
Wahrscheinlichkeit.
• Beispiel: Münze 2 mal werfen, X: Anzahl „Kopf“
8. Zufallsvariablen und
Verteilungen und Verteilungen
8. Zufallsvariablen
Beispiel Beispiel
(Z, Z)
65
(Z,K), (K,Z)
0,
(K,K)
64
0
1Anzahl X
Münzex2i malMwerfen;
X : werfen;
Kopf“
ünze
2 mal
:2 Anzahl Kopf“
”
”
xi
f .xi /
8̂
01
12
11
42
11
24
x<0
falls
05x<1
8̂
fallsx <1 05 x < 2
0; falls
x<0
ˆ
ˆ
ˆ
falls
0<
!41 ;x <falls
1 x0=!2 x < 1
4;
F.x/ D
2 3 F.x/ D
ˆ!3 ;x <falls
2 1!x<2
1 ˆ
ˆ
ˆ 4 ; falls 1ˆ
ˆ4
4 :̂
:̂
1; falls
2
1;x "falls
x"2
F (x) = 0;
1
1
1
ˆ
ˆ
f .Z;
(xi ) Z/ 4 .Z;.Z;
ˆ
2 Z/
4 Z/ .K; K/
K/;Z/
.K;
.K;.K;
K/
.Z; K/;
<1
0 xi
1
4 f .xi /
1
,
4
3
,
falls
4
1,
falls
falls
66
67
f .x/
F.x/
1
f .x/
3
4
1
2
1
!
4
!
0
1
1
2
1
!
4
!
0 2
!
x
1
1!
!
4
20
!
x
Bamberg et al.: Statistik
Bamberg et al.: Statistik
F.x/
!
1
3
4
1
!
4
1
0 2
!
x
1
!
2
x
71 j 223
9
71 j 223
3 Zufallsvariablen
1
3.2 Stetige Zufallsvariablen
• X heißt stetig, falls F (x) stetig ist.
68
• Dann gilt:
F (x) =
Zx
f (t) dt
−∞
• F 0 (x) = f (x) heißt Dichtefunktion von X.
• Zudem gilt:
69
3.2.1 Eigenschaften
70
•
f (x) = 0
für alle x ∈ R
71
Z∞
• Wegen F (∞) = 1 muss stets gelten:
f (x) dx = 1
−∞
72
•
73
•
P (X = x) = 0
für alle x ∈ R
F 0 (x) = f (x)
• Intervallgrenzen spielen keine Rolle:
74
P (X ∈ [a, b]) = P (X ∈ (a, b]) = P (X ∈ [a, b)) = P (X ∈ (a, b))
= F (b) − F (a)
10
Literatur
1
3.2.2 Beispiel
f (x) =


 0,
1
10 ,

 0,
falls
falls
falls
x < 0
0 5 x 5 10
x > 10
• Verteilungsfunktion:
75
3.3 Übungsaufgaben
[Pap11, Teil II, Zu Abschnitt 4, Seite 457ff]
Literatur
[BBK12] Günter Bamberg, Franz Baur und Michael Krapp. Statistik. 17. Auflage. Oldenbourg
Verlag, 2012.
[Pap11]
Lothar Papula. Mathematik für Ingenieure und Naturwissenschaftler. 6. Auflage.
Bd. 3. Vieweg + Teubner, 2011.
11