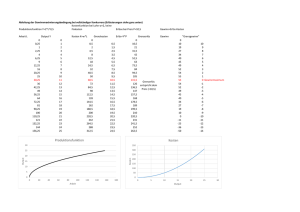
Kasten 1.3 Cournots Duopol

Kasten 1.3 Cournots Duopol
Mehr als hundert Jahre vor der Erfindung des Gefangenendilemmas und der Formulierung des
Nash-Gleichgewichts hat Cournot eine GD-Situation und das Prinzip des Gleichgewichts anhand
des Beispiels von zwei Unternehmen analysiert, die sich einen Mineralwassermarkt teilen. Wir
betrachten der Einfachheit halber ein Zahlenbeispiel mit der Nachfragefunktion P = 100 – (Q1 +
Q2), wobei P der Preis des Mineralwassers und Q1 und Q2 die von Firma 1 und Firma 2 angebotenen
Mengen sind (siehe z. B. Frank 1991). Firma 1 nimmt die vom Konkurrenten angebotene Menge Q2
als gegeben hin, d. h., aus der Sicht von Firma 1 gilt: P1 = (100 – Q2) – Q1. (Da die Situation symmetrisch ist, gilt entsprechend P2 = (100 – Q1) – Q2.) Der Erlös einer Firma ist der Preis multipliziert mit
2
der Menge. Firma 1 erlöst also E1 = P1 Q1 = Q1 (100 – Q2) – Q1 . Die Entscheidung der Firma richtet sich
auf die zu produzierende Menge. Firma 1 wird also, gegeben Q2, die Menge Q1 so wählen, dass der
Gewinn maximal ist. Der Gewinn ist maximal, wenn der Grenzerlös, also der Erlös für eine zusätzlich produzierte Einheit, den Grenzkosten entspricht. Den Grenzerlös erhalten wir durch Ableitung
der Erlösfunktion: dE1/dQ1 = 100 – Q2 – 2Q1. Es sei angenommen, die Kosten des aus dem Boden
sprudelnden Mineralwassers seien null (mit Grenzkosten größer als null ändert sich das Ergebnis
nicht). Die gewinnmaximierende Firma produziert dann 100 – Q2 – 2Q1 = 0 oder Q1 = 50 – 0,5Q2. Für
Firma 2 gilt analog: Q2 = 50 – 0,5Q1 oder Q1 = 100 – 2Q1. Diese beiden Kurven heißen Reaktionskurven. Man kann die beiden Kurven in einem Koordinatensystem mit Q1 an der y-Achse und Q2 an
der x-Achse darstellen. Ihr Schnittpunkt ist ein Cournot-Nash-Gleichgewicht. Man erhält als
Schnittpunkt der Reaktionsgeraden Q1* = Q2* = 33,33. Beide zusammen produzieren die Menge von
66,67 zu einem Preis von 100 – (Q1 + Q2) = 33,33. Der Erlös einer Firma beträgt also E1 = 33,33 • 33,33
= 1111. Man kann leicht prüfen, ob es sich um ein Nash-Gleichgewicht handelt. Produziert eine
Firma mehr (oder weniger) als die Gleichgewichtsmenge, sollte der Gewinn nicht ansteigen.
Wenn sich also Firma 1 entschließt, z. B. 34 oder 35 Einheiten zu produzieren, während Firma 2 bei
der Menge 33,33 bleibt, erzielt Firma 1 keinen Gewinnzuwachs. Wenn nun aber beide Firmen sich
wie die Gefangenen absprechen, ein Kartell bilden und die Menge Q = Q1 + Q2 so festlegen, dass
der gemeinsame Gewinn maximiert wird, können sie mehr verdienen. Sie verhalten sich dann zusammen wie ein Monopolist. Die Nachfragefunktion ist P = 100 – Q, die Erlösfunktion E = 100 Q –
2
Q , die Ableitung dE/dQ = 100 – 2Q. Bei Grenzkosten von null beträgt die gewinnmaximierende
Menge Qm = 50 oder Q1m = Q2m = 25 bei gleicher Aufteilung unter den beiden Firmen. Der Preis ist
dann 50 und der Gewinn 50 • 25 = 1250. Die Entscheidung für Qm ist Pareto-optimal. Jede Abweichung liefert Resultate, die für mindestens eine Firma schlechter sind. Die wechselseitige Wahl
der kooperativen Strategie Qm ist aber keine Nash-Gleichgewichtsstrategie. Dies lässt sich leicht
zeigen. Erhöht eine Firma die Menge, während sich die andere Firma an die Vereinbarung hält,
dann erzielt der Abweichler einen Gewinnzuwachs, während die kooperative Firma verliert. Produziert z. B. Firma 1 eine Menge von 33,33 Einheiten, dann sinkt der Preis auf 100 – 58,33 = 41,67.
Der Gewinn von Firma 1 steigt auf 41,67 • 33,33 = 1389, der Gewinn von Firma 2 sinkt auf 41,67 • 25
= 1042. Vereinfachen wir die Situation so, dass nur die beiden Strategien «Einhaltung der Kartellabsprache» (= Kooperation) und «Wettbewerb» (Defektion) in Betracht gezogen werden, erhalten
1
wir ein Gefangenendilemma:
Kartell (C)
Wettbewerb (D)
Kartell (C)
1250, 1250
1042, 1389
Wettbewerb (D)
1389, 1042
1111, 1111
Cournots Duopol kann in verschiedener Hinsicht verallgemeinert werden. So wird ein Unternehmen nicht die angebotene Menge der anderen Unternehmung als gegeben annehmen, sondern
den Preis. Weiterhin können mehrere Firmen auf dem oligopolistischen Markt agieren. Der
Grundkonflikt, die Spannung zwischen dem instabilen Pareto-Optimum und dem ineffizienten
Nash-Gleichgewicht, bleibt aber bestehen (dazu z. B. Frank 1991). Meistens sind Kartellabsprachen
illegal. Die Kooperation der Firmen schadet dem Verbraucher. Sie sind aber auch instabil, weil jede
Firma einen Anreiz hat, heimlich mehr zu einem geringeren Preis zu verkaufen. Verlangt der Gesetzgeber von den Unternehmen Transparenz bezüglich Preisen und Rabatten, weil man sich davon mehr Wettbewerb verspricht, so kann die Forderung in diesem Fall unerwünschte Folgen haben (Gintis 2000). Mehr Transparenz macht es schwieriger, eine Kartellvereinbarung heimlich zu
unterlaufen. Ein Kartell wird dadurch stabiler. Paradoxerweise könnte die sonst wettbewerbsfördernde Maßnahme bei Gefahr der Kartellbildung den Wettbewerb bremsen.
2