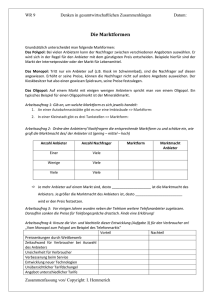
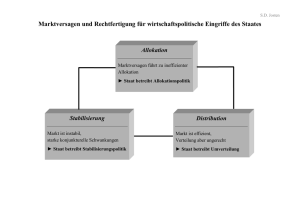
Teil III Gleichgewicht auf Märkten

Seite 1
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Teil III Gleichgewicht auf Märkten
Marktgleichgewicht:
g
g
Situation auf einem Markt, bei dem kein
Marktteilnehmer einen Anlass hat, sein Verhalten zu ändern.
9 Strategien im Polypol, Oligopol und Monopol
9.1 Gleichgewicht im Polypol
Annahmen/Charakteristika der vollkommenen Konkurrenz:
1. Ein völlig homogenes Gut wird angeboten/nachgefragt: keinerlei
Unterschiede sachlicher, zeitlicher, räumlicher, personeller Art aus
Sicht der Nachfrager
2 Einzelne Nachfrager und Anbieter haben keinen Einfluss auf den
2.
Preis: Preisnehmerschaft
3. Nachfrager
g und Anbieter haben alle relevanten Informationen über
das Gut: vollständige Information
Seite 2
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
4. Kostenloser Markteintritt für Anbieter
5. Keine Transaktionskosten, d.h. kostenlose
Verkaufsaktivitäten, keine Suchkosten u.ä.
Einkaufs-
⇒ Alle Marktteilnehmer verhalten sich als Preisnehmer;
es gibt keine Preisunterschiede
Typische Polypol-Situation mit vollkommener Konkurrenz:
- sehr viele,
viele kleine Nachfrager (relativ zum Gesamtmarktvolumen)
- sehr viele kleine Anbieter (relativ zum Gesamtmarktvolumen)
Zur Vereinfachung im Folgenden:
Viele, identische (kleine) Anbieter: identische Kostenfunktion
⇒ Betrachtung
g eines typischen
yp
Anbieters
und
Seite 3
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Analyse der Auswirkungen von Nachfrageveränderungen:
(s. Wiese (2002), S. 244ff. (Abschnitt L))
(i) Sehr kurzfristiges Marktgleichgewicht:
Bei wachsender Nachfrage von D0 auf D1 kann Angebot nicht
ausgeweitet werden (keine zusätzliche Beschaffung von
Produktionsfaktoren, keine neuen Anbieter)
⇒ Angebotsfunktion des typischen Anbieters ist horizontal:
p
Sskfr
p0
D0
0
y0 = y1
y
Seite 4
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Änderung des Gleichgewichtspreises
Nachfrageerhöhung von D0 auf D1 :
p
p0
sehr
kurzfristig
durch
Sskfr
p1
D1
p0
D0
0
y0 = y1
y‘
y
Entstehung von Überschussnachachfrage beim alten Preis p0.
⇒ Verschiedene Nachfrager (mit höherer Zahlungsbereitschaft als p0)
gehen leer aus.
aus
⇒ Diese werden mehr als p0 bieten.
⇒ Preissteigerungstendenz zu p1 hin.
⇒ Bei p1 Markt wieder im Gleichgewicht: dort Angebot = Nachfrage.
Seite 5
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
(ii) Kurzfristiges Marktgleichgewicht:
Nur
die variablen Produktionsfaktoren können angepasst (d.h.
(d h
gesteigert) werden.
⇒
Kurzfristige
(Grenz-)Kostenfunktion
ist
maßgeblich
für
A
Angebotsanpassung.
b t
Individuelles Optimum des typischen Anbieters aus
G ( y) = p ⋅ y − K kfr ( y) → max
(9.1)
p = K kfr ' ( y*) = SMC( y*)
(9 2)
(9.2)
und damit aus
Seite 6
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Grafisch (bei steigenden kurzfristigen Grenzkosten):
p
p
S0
D1
SMC
D0
SAC
p1
p0
0
q0
q1
Gesamtmarkt
q
0
y0
y1
y
typisches Unternehmen
Nachfragesteigerung
g
g
g von D0 auf D1 ⇒ Überschussnachfrage
g bei p0
⇒ Leer ausgegangene Nachfrager mit höherer Zahlungsbereitschaft
bieten mehr.
⇒ Für typischen Anbieter lukrativ,
lukrativ Angebot auszudehnen von y0 auf y1
nach (9.2).
Seite 7
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
(iii) Langfristiges Marktgleichgewicht:
Langfristig Anpassung aller Produktionsfaktoren an neue Nachfrage D1
und Eintritt neuer Anbieter auf Markt möglich und attraktiv, solange
positive Gewinne erzielt werden.
werden
⇒ Zunahme des Gesamtangebots von S0 auf S1, bis Gewinne auf 0
g g g sind.
zurückgegangen
p
p
D1
S0
D0
SMC
S1
LMC
SAC
p1
LAC
p0
0
q0 q1
q2
Gesamtmarkt
q
0
y0=y2 y1
typisches Unternehmen
y
Seite 8
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Bei vollkommenem Wettbewerb hat der (Gleichgewichts-)Preis
-
Informationsfunktion:
Knappheit
Preiserhöhung
g
-
Rationierungs- bzw. Lenkungs- und Koordinierungsfunktion:
Preiserhöhung bewegt (tendenziell) Nachfrager zur Einschränkung
und umgekehrt Anbieter zur Ausweitung des Angebots
signalisiert
g
größere
g
⇒ bei gestiegener Nachfrage wird Überschussnachfrage, bei
fallender Nachfrage Überangebot abgebaut.
Seite 9
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
9.2 Gleichgewicht im Oligopol
Literatur: Wiese ((2002),
) Abschnitt Q ((S. 373ff.))
Oligopol: einige wenige, relativ große Anbieter von gleichen bzw.
relativ ähnlichen (⇒ stark substitutiven) Produkten auf einem
Markt mit vielen Nachfragern mit dem
Charakteristikum:
Charakteristik
m
Erfolg (Absatz, Gewinn etc.) eines Anbieters hängt nicht nur von
seinem Verhalten (angebotene Menge, Preis seines Gutes) ab,
sondern auch vom Verhalten der übrigen Anbieter.
gegenseitige
g
g Abhängigkeit
gg
⇒g
⇒ spieltheoretische Situation
Seite 10
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Häufiges Vorkommen, z.B.:
Mineralölanbieter ((bzw. –förderländer))
Straßenfahrzeughersteller
Reifenhersteller
Zigarettenhersteller
Tankstelle
Bäcker
Friseure
Kaufhäuser
Vorsichtiges Agieren im Oligopol erforderlich, um erhebliche
Nachteile zu vermeiden.
Seite 11
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Wiederholungs-Beispiel aus 1. Kap.:
Duopol: zwei Anbieter desselben Produkts
Zwei Pizzahersteller können ihre Pizza zu niedrigem (2,50 €) oder
höherem Preis (3,00 €) anbieten.
⇒ Jeder Hersteller hat nur zwei Strategien: Niedrigpreis und Hochpreis.
Jeweilige Gewinne beim Aufeinandertreffen
„Auszahlungsmatrix“ aufgelistet:
der
Strategien
Unternehmen 2
Unternehmen 1
Gewinne in €
bei
p1 = 2,50 €
p2 = 3,00 €
p1 = 2
2,50
50 €
1 000 ; 1
1.000
1.000
000
1 500 ; 800
1.500
p2 = 3,00 €
800 ; 1.500
1.200 ; 1.200
in
Seite 12
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
⇒ gegenseitige Abhängigkeit der Gewinne
g
p Cournot-Nash-Gleichgewicht
g
((CNGG))
Gleichgewichtskonzept:
Definition:
Sei Si die Strategiemenge von Oligopolist i und Gi die Gewinnfunktion
von Spieler i (i=1,...,n). Die Strategiekombination (s1*,...,si*,...,sn*) ∈
S1×...×Si×...×Sn heißt Cournot-Nash-Gleichgewicht (CNGG) des
Oligopols genau dann, wenn
G
i
(s1* ,..., s*i ,..., s*N )
≥G
i
alle si ∈ Si ,
fü i = 1,...,
1 N
⎩ für
*
*
*
* ⎧für
(s1 ,..., si −1 , si , si +1 ,..., s N ) ⎨
((9.3))
⇒ Im CNGG für keinen Oligopolist (allein) Anreiz, von seiner
Gleichgewichtsstrategie (allein) abzuweichen.
abzuweichen
Es kann aber sehr wohl vorteilhaft für zwei oder mehr Spieler sein,
gemeinsam
i
von ihrer
ih Nash-Gleichgewichtsstrategie
N h Gl i h
i ht t t i abzuweichen.
b
i h
Seite 13
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Im obigen Duopol-Beispiel ist die Niedrig-Preis-Strategie ein CNGG
und zwar auch das einzige.
Erkennen eines CNGG im Zwei-Personen-Fall:
Das CNGG muss zugleich
g
das Spaltenmaximum
p
beim ersten und ein
Zeilenmaximum beim zweiten Oligopolisten sein.
Weitere Beobachtung am Beispiel oben:
Ein CNGG muss für die beteiligten Konkurrenten nicht unbedingt
b
besonders
d
günstig
ü ti sein:
i
Wenn verbindliche Absprache möglich wäre, könnten beide
Konkurrenten mit gemeinsamer Hochpreispolitik bedeutend besser
fahren.
Seite 14
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Im obigen Beispiel wäre das bei s po = (s12 , s 22 ) der Fall.
⇒ Das CNGG s* = (p11 , p12 ) ist nicht pareto-optimal.
pareto-optimal
Situation eines nicht pareto-optimalen (Cournot-)Nash-GG nennt man
eine
i (Gefangenen-)Dilemma-Situation:
(G f
)Dil
Sit ti
E ist
Es
i t individuell
i di id ll für
fü keinen
k i
Spieler vorteilhaft, das (Cournot-)Nash-GG (allein) zu verlassen;
aber für beide Spieler ist das CNGG wenig attraktiv: Bei
Kooperation könnten beide mehr erreichen.
⇒ Ist genau in Oligopolen häufig der Fall,
Fall aber auch in strukturell
ähnlichen Situationen, wie
- im (internationalen) Umweltschutz
Um eltsch t
- bei (Ab-)Rüstungsfragen
- bei Werbeaktivitäten
Seite 15
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Bemerkungen:
Es gibt Spiele mit mehr als einem (C)NGG; z.B.:
Unternehmen 2
UnternehUnterneh
men 1
Gewinne in €
bei
p1 = 2,50
, €
p2 = 3,00
, €
p1 = 2,50 €
800 ; 800
1.200 ; 900
p2 = 3,00 €
900 ; 1.200
1.100 ; 1.100
⇒ Die beiden Strategienkombinationen s* = (s12 , s12 ) und s * * = (s11 , s 22 )
sind Nash-GGe.
Nash GGe
Beide sind pareto-optimal; es besteht aber Anreiz zur Kooperation.
Seite 16
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Es gibt Spiele mit keinem (C)NGG; z.B.:
Unternehmen 2
Unternehmen 1
Gewinne in €
bei
p1 = 2,50 €
p2 = 3,00 €
p1 = 2,50
2 50 €
800 ; 900
1 200 ; 800
1.200
p2 = 3,00 €
900 ; 1.000
1.100 ; 1.200
Seite 17
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Die Unsicherheit über Reaktionen der Konkurrenten führt im
Oligopol zur Vorsicht.
⇒ Preise der Oligopolisten für homogene Produkte können nicht
sehr stark differieren, und zwar um so weniger,
je ähnlicher ihre Produkte und
je vollkommener der Markt für die Nachfrager
ist.
Bei praktisch gleichen Gütern und vollkommener Markttransparenz
bildet sich ein einheitlicher Preis.
Beispiele: Preise für Benzin an Tankstellen, für Fertigpizza in
Supermärkten, für Zigaretten usw.
Seite 18
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Idealtypische Modellierung einer Oligopolsituation:
- Oligopolisten
g p
sind Preisnehmer.
- Sie können nur ihre jeweilige Angebotsmenge variieren.
-
n
Der Marktpreis p hängt von der Gesamtangebotsmenge ∑ x i
i =1
aller Oligopolisten ab.
Analyse
zunächst
für
Verallgemeinerung:
p = f(x1 + x2)
nur
zwei
mit f‘ < 0
Oligopolisten,
später
(9.4)
f ist inverse Nachfragefunktion: Sie gibt zu jeder GesamtangebotsGesamtangebots
bzw. –nachfragemenge denjenigen Preis p an, zu dem dieses
Gesamtangebot auch nachgefragt wird.
Seite 19
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Gewinnfunktion des ii-ten
ten Oligopolisten:
G i ( x 1 , x 2 ) = p ⋅ x i − K i ( x i ) = x i ⋅ f ( x1 + x 2 ) − K i ( x i )
(9.5)
⇒ Kein Oligopolist kann isoliert (d.h. unabhängig von seinem
Konkurrenten) seinen Gewinn maximieren.
Notwendige Bedingungen für inneres Maximum des O1 bzw. O2:
∂G1 ( x1*,
* x2 )
0=
= f ( x1* + x 2 ) + x1* ⋅ f ' ( x1* + x 2 ) − K1 ' ( x1* )
∂x1
(9.6)
∂G 2 ( x1 , x *2 )
0=
= f ( x1 + x *2 ) + x *2 ⋅ f ' ( x1 + x*2 ) − K 2 ' ( x*2 )
∂x 2
⇒ Auflösung der ersten Gleichung nach x1* hängt von x2 ab und
Auflösung der zweiten Gleichung nach x2* hängt von x1 ab:
Seite 20
Stehling | AVWL 3 (Mikro) | SS 08
⇒
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
x1* = R1(x2)
und
x2* = R2(x1)
R1 und R2 heißen Reaktionsfunktionen der Oligopolisten.
g p
⇒ Je nach dem, welche Menge der Konkurrent anbietet, ist eine andere
Menge für einen Oligopolisten gewinnmaximal!
Beispiel:
Die inverse Nachfragefunktion sei
p = f ( x1 + x 2 ) = −5 ⋅ ( x1 + x 2 ) + 100
Die Kostenfunktionen:
K1 ( x1 ) = ( x1 ) 2 + 2
⇒
K 2 (x 2 ) = 2 ⋅ (x 2 )2 + 1
G1 ( x1 ) = x1 ( −5 ⋅ ( x1+ x 2 ) + 100) − ( x1 ) 2 − 2
G 2 ( x 2 ) = x 2 (−5 ⋅ ( x1 + x 2 ) + 100) − 2( x 2 ) 2 − 1
Seite 21
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Notwendige Bedingungen für inneres Maximum des O1:
∂G1 ( x1*,
* x2 )
0=
= −5 ⋅ ( x1 * + x 2 ) + 100 + x1 * ⋅(−5) − 2 x1 *
∂x1
⇒
x1* = −
5
100
x2 +
=: R1 ( x 2 )
12
12
⇒ x1* um so kleiner, je größer x2 .
R1 ist die Reaktionsfunktion des O1 .
(9 7)
(9.7)
Seite 22
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Entsprechendes für den O2:
Notw. Bedingung
g g für ((inneres)) Gewinnmaximum des O2:
∂G 2 ( x1 , x 2 *)
0=
= −5( x1 + x 2 *) + 100 + x 2 * ⋅(−5) − 4 x 2 *
∂x 2
⇒
x 2* = −
5
100
x1 +
=: R 2 ( x1 )
14
14
⇒ Je größer x1 , um so kleiner das gewinnmaximale x2*.
R2 ist die Reaktionsfunktion des O2.
(9.8)
Seite 23
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Frage:
Welche Mengen x1 und x2 sollten die beiden Duopolisten (bzw. im
allgemeinen Fall die Oligopolisten) jeweils anbieten,
anbieten wenn
Kooperation (Absprache) nicht erlaubt ist?
Bieten
Bi
t z.B.
B (in
(i einer
i
A f
Anfangssituation)
it ti ) O1 und
d O2 jeweils
j
il die
di Mengen
M
x1 = x2 = 5 an, so erzielen sie (mit der Gesamtnachfrage X := x1 + x2
= 10) die Gewinne
G1 (5;5) = −25 ⋅ 10 + 100 ⋅ 5 − 25 − 2 = 223
G 2 (5;5) = −25 ⋅ 10 + 100 ⋅ 5 − 2 ⋅ 25 − 1 = 199
Versucht O1 seinen Gewinn durch Erhöhung seiner Angebotsmenge
a f x1 = 7 und
auf
nd bleibt O2 bei seiner Angebotsmenge x2 = 5,
5 so ist
jetzt X := x1 + x2 = 12 .
Seite 24
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
⇒
G1 (7;5) = −35 ⋅ 12 + 700 − 49 − 2 = 229
G 2 (7;5) = −25 ⋅ 12 + 500 − 50 − 1 = 149
⇒ O1 steigert seinen Gewinn auf Kosten von O2.
O2
Erhöht nun auch O2 seine Menge auf x2 = 7, so ist X = 7 + 7 = 14 und
G1 (7;7) = −35 ⋅ 14 + 700 − 49 − 2 = 159
G 2 (7;7) = −35 ⋅ 14 + 700 − 98 − 1 = 111
⇒ Die Gewinne beider sinken.
⇒ Weitere Mengenveränderungen
wahrscheinlich.
zur
Gewinnsteigerung
sehr
Seite 25
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Wann gibt es keine Anreize zu Mengenveränderungen der beiden
Oligopolisten?
Antwort: Im Cournot-Nash-GG
( x1CN , x CN
2 .)
Nach Definition ist das bestimmt durch die Ungleichungen
1
CN
G1 ( x1CN , x CN
2 ) ≥ G ( x1 , x 2 )
G
2
( x1CN , x CN
2 )
≥G
2
( x1CN , x 2 )
für alle x1 ≥ 0
für alle x2 ≥ 0
(9.9)
i
⇔ ( x1CN , x CN
2 ) maximiert die Gewinnfunktion G bzgl. xi bei festem Wert
xjCN des anderen.
⇔ ( x1CN , x CN
2 ) ist gerade eine Lösung des Gleichungssystems (9.6).
Seite 26
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Preis pCN im CNGG über die inverse Nachfrage gegeben durch
pCN = f ( x1CN + x CN
) =: f (X CN )
2
14243
((9.10))
= X CN
Damit lauten die notwendigen Bedingungen (9.6)
(9 6)
pCN = K i ' ( x iCN ) − x iCN ⋅ f ' ( X CN )
oder
K i ' ( x iCN ) = pCN + x iCN ⋅ f ' ( X CN )
mit
X
CN
2
:= ∑ x iCN
i =1
=1
für i = 1,2
(9.6‘)
Seite 27
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Geometrisch ergibt sich das CNGG im Fall n=2 als Schnittpunkt der
beiden Reaktionsfunktionen R1 und R2 :
x2
R1
x CN
2
R2
0
x1CN
x1
Seite 28
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Im Fall des obigen Duopol-Beispiels ergibt sich:
x1CN ≈ 6,3
x CN
2 ≈ 4,9
Dabei erreichte Gewinne von O1 und O2:
G1 ( x1CN , x CN
2 ) ≈ 235,5
G 2 ( x1CN , x CN
2 ) ≈ 166,6
Der Marktpreis im CNGG ist dann
pCN = f ( x1CN + x CN
2 ) ≈ 44
Seite 29
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
9.3 Gewinnmaximierung im Monopol
Monopol als „Grenzfall“ des Oligopols:
Oligopolisten sind Töchter eines Gesamtunternehmens („Monopolist“)
unter
zentraler
Leitung
( Kartell Situation“)
(„Kartell-Situation“),
das
nur
Gesamtgewinnmaximierung verfolgt.
⇒ Erlaubt Vergleich mit „normaler
„normaler“ Oligopol
Oligopol-Situation.
Situation.
Zur
Vereinfachung
Unternehmen.
zunächst
Betrachtung
nur
zweier
Töchter-
Seite 30
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
⇒ Gesucht sind solche Mengen x1M , x M
2 , die Lösungen sind von
G M ( x1 , x 2 ) = G1 ( x1 , x 2 ) + G 2 ( x1 , x 2 ) =
2
2
j=1
j=1
j
2
2
j=1
j=1
= ∑ p ⋅ x j − ∑ K (x j ) = p ⋅ ∑ x j − ∑ K j (x j ) =
2
2
2
j=1
j=1
j=1
(9.10)
= f ( ∑ x j ) ⋅ ∑ x j − ∑ K j ( x j ) → max .
Notwendige Bedingung für (innere) Lösungen x1M , x M
2
2
2
2
∂G M
i
M
M
M
0=
= f ( ∑ x j ) + ∑ x j ⋅ f '( ∑ xM
j ) − K ' (xi )
∂x i
j=1
j=1
j=1
oder mit
2
2
j=1
j=1
M
M
M
X M := ∑ x M
j und p := f ( ∑ x j ) = f ( X )
:
Seite 31
Stehling | AVWL 3 (Mikro) | SS 08
bzw.
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
p M = K i ' ( x iM ) − X M ⋅ f ' (X M )
((9.11‘))
K i ' ( x iM ) = p M + X M ⋅ f ' (X M )
(9.11)
Rechte Seite von (9.11) unabhängig von i.
⇒ Linke Seite von (9.11) unabhängig von i.
⇒ Im Gesamtgewinnmaximum sind die Grenzkosten aller Anbieter
gleich.
⇒ Bei konvexen Kostenfunktionen produziert dasjenige Unternehmen
mehr
im
Gesamtgewinnmaximum
Gesamtgewinnmaximum,
das
die
geringeren
Grenzkosten hat (umgekehrt bei konkaven Kostenfunktionen).
Veranschaulichung
g an Grafik:
Seite 32
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Konkave Kostenfunktionen: Ki’ fällt monoton:
Ki’
K1’
a
K2’ < K1’
0
x 2*
x1*> x2*
x
Konvexe Kostenfunktion: Ki’ wächst monoton:
Ki’
K1’
K2’ < K1’
a
0
x1*< x2*
x 2*
x
Seite 33
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Vergleich von gewinnmaximalem Monopolpreis und Absatzmengen mit
Gleichgewichtspreisen und –mengen im Oligopol:
⇒ Zu vergleichen die Lösungen der beiden Gleichungssysteme:
K
i
K
i
' ( x iCN )
' ( x iM )
=
=
2
f ( ∑ x CN
k )+
k =1
2
x iCN
2
M
f ( ∑ xk ) + ∑ xM
k
k =1
k =1
2
⋅ f ' ( ∑ x CN
k )
k =1
2
⋅ f '( ∑ xM
k )
(i=1 2)
(i=1,2)
(9 6‘)
(9.6‘)
(i=1,2)
(i
1,2)
(9.11)
k =1
Wir werden zeigen:
Falls die Kostenfunktionen der Anbieter konvex sind (d.h. Ki’’> 0) und
ff’’ ≤ 0 für die inverse Nachfragefunktion f ist,
ist gilt:
Seite 34
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
n
CN
∑ xk
k =1
n
≥ ∑ xM
k
(9.12)
k =1
d.h. die Gesamtangebotsmenge im CNGG des Oligopols ist mindestens
so groß wie im Monopol.
p
CN
=
n
f ( ∑ x CN
k )
k =1
n
M
≤ f ( ∑ xM
k )=p
k =1
(9.13)
d.h. der Preis im CNGG des Oligopols ist höchstens so hoch wie der
gewinnmaximale Preis im Monopol.
Seite 35
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Beweis:
Angenommen, (9.12) wäre nicht richtig. ⇒
n
CN
∑ xk
k =1
n
< ∑ xM
k
k =1
(+)
⇒ ∃ mindestens ein i mit
x iCN < x iM
((++))
Für dieses i gilt mit (9.11) und (9.6’) wegen f’ < 0, f’’ ≤ 0 und (+) dann:
Seite 36
Stehling | AVWL 3 (Mikro) | SS 08
K
<
<
≤
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
i
' ( x iM )
=
n
n
M
M
f ( ∑ xk ) + ( ∑ xk ) ⋅ f '( ∑ xM
k )
k =1
k =1
k =1
n
f ( ∑ x CN
k )+
k =1
n
f ( ∑ x CN
k )+
k =1
n
f ( ∑ x CN
k )+
k =1
n
x iM
<
n
⋅ f '( ∑ xM
k )<
x iCN
x iCN
k =1
n
⋅ f '( ∑ xM
k )≤
k =1
n
⋅ f ' ( ∑ x CN
k )=
k =1
= K i ' ( x iCN )
Also wäre
K i ' ( x iM ) < K i ' ( x iCN ) ,
woraus wegen Ki’’ > 0 sofort
x iM < x iCN
folgte, im Widerspruch zu (++). Also war die Annahme (+) falsch, also
gilt ((9.12).
g
)
Seite 37
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
(9.13) folgt sofort aus (9.12) und der Annahme, dass die inverse
Nachfragefunktion monoton fällt, d.h. f’ < 0 gilt.
⇒ Oligopolsituation ist (unter den getroffenen Annahmen) für die
Nachfrager günstiger als eine Monopolsituation.
⇒ Grund für Verbot von Absprachen von Konkurrenten auf einem
Markt und für kritische Prüfung von Unternehmenszusammenschlüssen durch das Kartellamt.
Durch ähnliche Analyse
Voraussetzungen):
auch
nachweisbar
(unter
ähnlichen
Gesamtnachfragemenge im Gleichgewicht des Polypols ist
mindestens so g
groß ist wie Gesamtnachfrage
g im CNGG des
entsprechenden Oligopols und
Gleichgewichtspreis im Polypol ist höchstens so hoch wie Preis im
CNGG des entsprechenden Oligopols.
Seite 38
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Betrachtung des Duopol
Duopol-Beispiels
Beispiels von oben für den Fall der
Kooperation beider Anbieter und Gesamtgewinnmaximierung:
Gesamtgewinn beider Anbieter:
G M ( x1 , x 2 ) = G1 ( x1 , x 2 ) + G 2 ( x1 , x 2 )
= x1 ( −5 ⋅ ( x1+ x 2 ) + 100) − ( x1 ) 2 − 2 +
+ x 2 (−5 ⋅ ( x1 + x 2 ) + 100) − 2( x 2 ) 2 − 1 =
= −5x12 − 5x1x 2 + 100 x1 − x12 − 2 − 5x1x 2 − 5x 2 2 + 100 x 2 − 2 x 2 2 − 1
⇒
∂G M
= −10 x1 − 5x 2 + 100 − 2 x1 − 5x 2 =
∂x1
= −12 x1 − 10x 2 + 100 = 0
und
∂G M
= −5x1 − 5x1 − 10 x 2 + 100 − 4 x 2 =
∂x 2
= −10 x1 − 14 x 2 + 100 = 0
Seite 39
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
⇒ Lösung
und
d
x1M =
4800
≈ 5,9 < 6,3 ≈ x1CN
816
xM
2 =
200
≈ 2,9 < 4,9 ≈ x CN
2
68
bei einem Marktpreis von
p M = f ( x1M + x 2M ) = −5 ⋅ 8,8 + 100 = 56 > 44 = p CN
mit einem maximalen Gesamtgewinn von
G M ( x1M , x M
2 )=
= −6 x12 − 10 x1x 2 + 100 x1 − 2 − 7 x 2 2 + 100 x 2 − 1 =
≈ 438
2
CN
CN
> 235,5 + 166,6 = 402,1 = G1 ( x1CN , x CN
2 ) + G ( x1 , x 2 )
Seite 40
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
⇒ Bestätigung der oben gemachten Aussagen (das Beispiel erfüllt alle
dortigen Voraussetzungen mit f‘‘ = 0 wegen der Linearität der
inversen Nachfragefunktion).
g
)
In der Praxis nicht selten Kartellbestrebungen.
Beispiele:
•
•
•
OPEC-Kartell (internationale Absprachen über Fördermengen zur
Ölpreis-Beeinflussung)
Absprachen von Zementherstellern
Absprachen zwischen europäischen Herstellern von Kupferhalbzeug
Außerdem Unternehmenszusammenschlüsse zur Erzielung
stärkeren Marktstellung mit Preisbeeinflussungsmöglichkeit.
einer
Seite 41
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Weitere Strategie von Oligopolisten zur Entschärfung des Wettbewerbs:
Produktdifferenzierung:
Prod
ktdifferen ier ng Heterogenisierung
Heterogenisier ng von
on Produkten:
Prod kten
Schaffen von Zusatznutzen durch neue Produkteigenschaften
(z.T. „symbolische“, z.B. durch Schaffung von Markenbewusstsein)
⇒ Erreichen einer unique selling position (USP)
⇒ monopolistische
p
Preisgestaltungsmöglichkeiten
g
g
g
Seite 42
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
Viel Erfolg bei den anstehenden Klausuren
und
eine schöne vorlesungsfreie Zeit („Semesterferien“)!
Seite 43
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
oder
Seite 44
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 9: Strategien im Polypol, Oligopol und Monopol -
oder