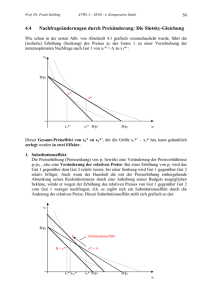
Gesamtnachfrage

Seite 1
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
5 Gesamtwirtschaftl.
Gesamtwirtschaftl Nachfragefunktionen
ges
Gesamtwirtschaftliche Nachfrage x i
nach einem Gut i:
Summe aus den individuellen Nachfragen n ik :
x iges =
N k*
∑ xi
k =1
=
N k
k
∑ n i ( p1 ,..., p n , B )
k =1
⇒ Abhängigkeit der Gesamtnachfrage eines Gutes vom
-
vom Preis desselben Gutes
von den Preisen anderer Güter
von den Budgets der HHe
den Präferenzen der HHe
(5.1‘)
Seite 2
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Gesamtnachfrage eines Gutes meist nur in Abhängigkeit vom Preis
dieses Gutes betrachtet; vereinfacht also:
x iges =
N k
∑ n i (..., pi ,...)
k =1
=: N i ( pi )
Häufig nur auch jeweils ein Gut betrachtet,
betrachtet so dass Index i weggelassen
wird:
x = N(p)
N heißt Gesamtwirtschaftliche Nachfragefunktion oder aggregierte
Nachfragefunktion.
Seite 3
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Mit den ni ist auch N als deren Summe (streng) monoton wachsend;
also grafisch:
g
x = N(p)
0
p
Seite 4
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Maß für die absolute Stärke der Abhängigkeit der Gesamtnachfrage
nach dem Gut von seinem Preis p:
dN( p) N( p + ∆p) − N(p) (∆p = 1)
≈
N (p + 1) − N (p)
≈
∆p
dp
(5.2)
Maß für die relative Stärke der Preisabhängigkeit
Gesamtnachfrage: Preiselastizität der Gesamtnachfrage:
ε N; p :=
dN(p) p
dp N(p)
(5 3)
(5.3)
der
Seite 5
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Normale Gesamtnachfrage:
⇔
dN
≤0
dp
Anormale Gesamtnachfrage:
⇔
dN
>0
dp
(preis-)elastische Gesamtnachfrage:
⇔ ε N ; p < −1
(preis-)unelastische Gesamtnachfrage: ⇔ ε N; p < −1
Seite 6
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Beispiel:
lineare Gesamtnachfrage:
g
x = N(p) = a - b·p mit positiven Konstanten a, b > 0
⇒ x = a ist die Sättigungsmenge wegen N(0) = a;
und
p = a/b ist Prohibitivpreis wegen N(a/b) = 0.
Seite 7
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Grafisch:
x=N(p)
a
0
b/2a
b/a
p
Seite 8
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Für x = N(p) = a - b·p ist
dN
= −b < 0
dp
ε N ; p ( p) = − b ⋅
p
p
= −b ⋅
a − b⋅p
N ( p)
und daher:
bp
a
a
⇔p=
⇔N=
a − bp
2b
2
ε N; p ( p) = −1
⇔ −1 = −
ε N ; p ( p) = 0
⇔p=0⇔x=N=a
ε N ; p ( p) = ∞
⇔p=
a
⇔x=N=0
b
(5.5)
Seite 9
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Für manche Untersuchungen praktischer:
Inverse der Nachfragefunktion,
g
d.h. Zusammenhang
g x = N(p)
(p)
umdrehen in
p = N-1(x)
(5 6)
(5.6)
⇒ Sichtweise hier umgekehrt:
N-1(x) gibt an, bei welchem Preis p eine bestimmte Nachfragemenge
x erreicht wird.
Grafisch: Spiegelung von N(p) an der Winkelhalbierenden
Seite 10
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Beispiel:
Für die oben verwendete lineare Nachfragefunktion
x = a – bp = N(p)
ist (durch Auflösung nach p)
1
a
p = − x + =: −ex + c =: N −1 ( x )
b
b
(5.7)
⇒ Gerade mit der Steigung –1/b und mit dem Ordinatenabschnitt
a/b
Seite 11
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Für viele mikroökonomische Untersuchungen interessant:
Produkt aus Preis und dabei nachgefragter
g
g Menge
g ((= revenue R),
) also
R (p) = p ⋅ x = p ⋅ N (p) = N −1 ( x ) ⋅ x =
⎧Ausgabe für das Gut aus Sicht der Nachfrager
=⎨
⎩ Umsatz/Erlös aus Sicht eines Unternehmens
Z.B. interessant für ein Unternehmen zu wissen, bei welchem
Preis(bereich) sein Umsatz/Erlös maximal ist.
Antwort: dort, wo Ableitung des Umsatzes (= marginal revenue = MR)
gleich 0 ist.
Seite 12
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
⇒ Bilde (wie bei individuellen Nachfragefunktionen)
MR (p) =
dR ( p)
dN( p)
= N ( p) + p
=
dp
dp
⎛ dN (p) p ⎞
= N(p)⎜1 +
⎟ = N (p)(1 + ε x ; p (p))
dp N (p) ⎠
⎝
(Formel von Amoroso
Amoroso-Robinson).
Robinson).
⇒ Notwendige Bedingung für Umsatzmaximum:
0 = MR ( p*) ⇔ ε x ; p ( p*) = −1
⇒ Die Umsatz-(bzw. Ausgaben)funktion wird dort (d.h. bei dem
Preis p*) maximal, wo die Preiselastizität der Nachfrage gleich
-1 ist.
Seite 13
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Beispiel:
Für die lineare Nachfragefunktion
g
N(p)
(p) = a – bp
p ist
R ( p) = p(a − bp) = ap − bp 2
⇒
MR (p*)) = R ' (p*)) = a − 2bp* = 0
⇔ p* =
a
2b
Seite 14
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Methoden
zur
empirischen
Nachfragefunktionen
bzw.
Überblick:
Bestimmung
von
PreisZahlungsbereitschaften
im
Quelle: Frohs, M., Backhaus,K. (2008), S. 7
Seite 15
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Abhängigkeit der Gesamtnachfrage auch von anderen Einflüssen
⇒ Verschiebung
g der Gesamtnachfragekurve,
g
z.B. insbesondere
durch
-
Preise anderer Güter (Substitute,
(Substitute komplementäre Güter)
-
das Einkommen der HHe
-
die Anzahl der HHe bzw. Nachfrager
-
die Präferenzen der HHe für das Gut
-
Werbung (für das Produkt)
-
Erwartungen über
- zukünftige Preise
- zukünftige Einkommen
Seite 16
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
In höchster Aggregation (makroökonomischer Level):
Gesamtwirtschaftliche Nachfrage =
gesamtwirtschaftlicher Konsum (C)
+
gesamtwirtschaftliche Investition (I)
+
gesamtwirtschaftlicher Export (Ex)
Seite 17
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Wichtigkeit von Kaufentscheidungskriterien bei Lebensmitteln
(Quelle:
L it
Leitow
(2005)
(2005),
S. 77):
Seite 18
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Wichtigkeit von Kaufentscheidungskriterien bei Lebensmitteln
in Abhängigkeit vom Alter:
Quelle: Leitow (2005), S. 81
Seite 19
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 5: Gesamtwirtschaftliche Nachfragefunktionen
Wichtigkeit von Kaufentscheidungskriterien bei Lebensmitteln
in Abhängigkeit von der Herkunft des Probanden
(Quelle: Leitow (2005), S. 82):