Teil B: Theorie des Angebots

Seite 1
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Teil B: Theorie des Angebots
Literatur: Wiese (2001),
(2001) S.
S 139 ff.
ff (Abschnitt G).
G)
In Parallelität zur Haushaltstheorie:
In der Unternehmenstheorie: Erklärung/Ableitung des Gesamtangebots
für ein marktfähiges Gut aus den individuellen Entscheidungen
einzelner Unternehmen
Unternehmen
bzw.
sein
Management
hat
Wertbzw.
Zielvorstellungen und versucht, diese möglichst gut zu
realisieren:
Unternehmen bzw. Unternehmer als homo oeconomicus: handeln
nach einem Rationalitätsprinzip.
p
p
Seite 2
Stehling | AVWL 3 (Mikro) | SS 08
Volkswirtschaftliche
Unternehmen:
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
und
gesellschaftliche
Aufgabe
von
Produktion bzw. Bereitstellung von Gütern/Leistungen zur
•
Bedürfnisbefriedigung von inländischen und ausländischen
Haushalten (⇒
( Nachfrage nach Konsumgütern: B2C-Geschäfte)
B2C Geschäfte) und
zur
•
Befriedigung
der
Nachfrage
anderer
(inländischer
oder
ausländischer) Unternehmen (⇒ Produktionsgüter; B2B-Geschäfte)
Treibendes Moment in einer Marktwirtschaft:
Erzielung von „Einkommen“ aus dieser Produktionstätigkeit und
dem Verkauf der Produkte/Leistungen
Seite 3
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Grundansatz der Angebotstheorie:
Gewinnmaximierung
g als g
ganz vorrangiges
gg
einzelwirtschaftliches Ziel
von Unternehmen
⇒ Entsprechung zur Nutzenmaximierung bei Haushalten im Rahmen
der Haushaltstheorie
Bei realen unternehmerischen Entscheidungen noch viele andere
Motive/Ziele: insbesondere
•
•
•
•
•
•
Gesamtkapitalrendite (ROI)
Eigenkapitalrendite
Produktivität
Marktanteil
Cash-Flow/Liquidität
Wertschöpfung
Seite 4
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Sowie
•
•
•
•
•
Innovationsfähigkeit
g
((⇒ neue Produkte))
Kundentreue
Image/Reputation
Mitarbeiterloyalität
Arbeitsplatzsicherheit
•
•
Umweltschutz
(weitere) gesellschaftsbezogene und soziale Ziele
Aus Sicht des externen Rechnungswesens:
Gewinn G (in einer Zeiteinheit) =
= Saldo aus allen Erträgen und allen Aufwendungen (in dieser
Zeiteinheit)
Seite 5
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Aus Sicht des internen Rechnungswesens (genauer: der Kosten- und
Leistungsrechnung):
Gewinn G = Saldo aus allen Umsatzerlösen und den Kosten
In starker Vereinfachung:
Unternehmen stellt nur ein einziges Gut her:
G ( x ) = Umsatz − Kosten = p ⋅ x − K ( x )
p = Preis des Gutes
x = produzierte und abgesetzte Menge des Gutes
K(x) = (Gesamt-)Kosten
(Gesamt )Kosten für Produktion und Absatz von x
Seite 6
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Abgesetzte (bzw. absetzbare) Menge x eine (normalerweise streng
monoton fallende) Funktion N (insbesondere) des Preises p dieses
Gutes ((und weiterer, jjetzt vernachlässigter
g
Einflüsse)) mit
Umkehrfunktion N-1 :
G ( x ) = p ⋅ x − K ( x ) = N −1 ( x ) x − K ( x ) → max
(Φ1)
Lösung x
x* von (Φ1) liefert die individuelle gewinnmaximale
Angebotsmenge des betreffenden Unternehmens.
⇒
Analogie der Angebotstheorie
Nachfragetheorie
zum
Problem
(P1)
der
(Implizite) Restriktion dabei: Produktion ist an die jeweils vorhandene
Technologie gebunden ⇒ Auswirkung auf Kostenfunktion K
Seite 7
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Wichtige Unterschiede zwischen (Φ1) und (P1):
((i)) Gewinn eines Unternehmens ist monetäre und ungleich
g
realere
Größe als der Nutzen eines Haushalts.
(ii) Umsatz eines Unternehmens häufig nicht nur von dessen
Entscheidungen abhängig,
abhängig sondern auch von denen anderer
Marktteilnehmer; z.B. von den Nachfragern und meist auch vom
Angebot der Konkurrenten (⇒ Marktsituation)
⇒ erheblich geringere Autonomie und größere Interdependenz
(iii) Kostenfunktion K des Unternehmens hängt stark von seiner
Technologie T ab.
Output x alternativ mit unterschiedlichen Mitteleinsätzen (Inputs)
herstellbar
⇒ x durch möglichst kostengünstige Inputs herzustellen; d.h. die
Kosten
K(x)
sind
bereits
selbst
Ergebnis
eines
Kostenminimierungsprozesses.
g p
Seite 8
Stehling | AVWL 3 (Mikro) | SS 08
7 Grundlagen
theorie
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
der
Produktions-
und
Kosten-
Produktion technisch gesehen:
Transformation von Inputs (= Produktionsfaktoren) in Outputs (=
Produkte/Leistungen)
Bei
Ein Produkt Unternehmung
Ein-Produkt-Unternehmung
funktion (PF) f, d.i.
beschreibbar
durch
ProduktionsProduktions
Zuordnung:
Kombination von Produktionsfaktoren z = (z1,...,zi,...,zm) → maximal
damit herstellbare Outputmenge y = f(z):
y = f ( z) = f ( z1 ,..., z m )
mit zi = Menge
g vom i-ten Input.
p
(6.1)
Seite 9
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Empirisch von f meist nur einige Punkte bekannt.
Vervollständigung
g g aus empirischen
p
Daten durch Regressionsansätze
g
möglich:
y=f(...,zi,...)
+
+
+
+
+
+
+
+
+
0
zi
Seite 10
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
-
meist zahlreiche, vielfältige Inputs
-
komplexe
p
Zusammenhänge
g zwischen Inputs
p
und Outputs,
p
oft nicht
ohne weiteres analytisch und quantitativ angebbar
-
⇒ erhebliche Vereinfachungen nötig; z.B. durch starke Abstraktion
und Aggregation von Inputs zu großen Gruppen (z.B.
(z B zum
Produktionsfaktor „Arbeit“ und „Kapital“)
Ausgewählt einfache bzw. stark vereinfachte Beispiele:
Seite 11
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
1. Herstellung von "Studentenfutter" aus Haselnüssen, Paranüssen,
Walnüssen und Rosinen;
nur Gesamtgewicht
g
der Mischung
g wichtig,
g nicht Zusammensetzung
g
aus den Bestandteilen (⇒ vollständige Substituierbarkeit der
Inputs):
zugehörige PF f hat die Gestalt:
y = f (z1 , z 2 , z 3 , z 4 ) = z1 + z 2 + z3 + z 4
mit
y = Gesamtgewicht
g
der Mischung
g
zi = Gewicht des i-ten Bestandteils
⇒ Beispiel für eine substitutionale Produktionsfunktion
(6.2)
Seite 12
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
2. Herstellung von Tischen:
Annahme: Pro Tisch werden gebraucht an Inputs:
•
•
•
1 Tischplatte
4 Tischbeine
2 Arbeitseinheiten
⇒
streng
g
komplementäre
p
Produktionszusammenhang:
Inputs
p
mit
⎧z z z ⎫
y = f (z ) = f (z1 , z 2 , z3 ) = min
i ⎨ 1, 2 , 3⎬
⎩1 4 2 ⎭
⇒ Prototyp einer (linear-)limitationalen PF f.
limitationalem
(6 3)
(6.3)
Seite 13
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
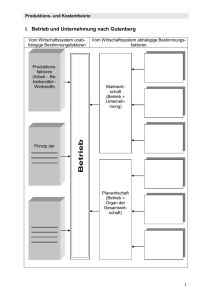
3. Volkswirtschaftliche Produktionsfunktion:
Vorstellung:
Vorstell
ng BIP Y(t) im Jahr t kommt zustande
stande durch
d rch Einsatz
Einsat der
hochaggregierten Produktionsfaktoren:
•
•
•
Menschlicher Arbeitseinsatz A (in Arbeitsstunden)
Kapitaleinsatz K (in monetärer Einheit)
g
E ((in g
geeigneten
g
Energieeinheiten)
g
)
Energieeinsatz
BIPt = Y ( t ) = f (A, K, E, t ) = ceλt A α K β E γ
(6.4)
mit gewissen Konstanten c, λ, α, β, γ > 0
Term eλt repräsentiert Wirken des technischen Fortschritts.
Schätzung der Konstanten aus empirischen Daten
Regressionsansätze.
g
durch
Seite 14
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Voraussetzungen (zur Vereinfachung) im Folgenden:
Inputs
Inp
ts und
nd Output(s)
O tp t(s) beliebig teilbar ⇒ zi , y ∈ IR+
f hinreichend glatt, d.h. hinreichend oft (partiell) differenzierbar
Bezeichnungen zur Vereinfachung:
∂f (z)
∂ 2f ( z )
∂ 2f (z)
fi (z) :=
, fij (z) :=
, fii (z) :=
∂zi
∂zi ∂z j
∂z i2
Seite 15
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Einige produktionstheoretische Grundbegriffe:
f (z)
zi
= Durchschnittsprodukt(ivität)
D rchschnittsprod kt(i ität) von
on Input
Inp t i
(average productivity of input i, APi)
f i (z) = Grenzprodukt(ivität) von Input i
(marginal productivity of input I, MPi)
Interpretationen (anschauliche Bedeutungen)
Seite 16
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Mögliche Auswirkungen auf den Output verschiedener Änderungen
der Produktionsfaktoren:
Steigerung der Einsatzmenge eines einzelnen Inputs (= „partielle
Faktorvariation“) senkt normalerweise den Output nicht:
⇒ f ist monoton wachsend in jedem einzelnen zi :
MPi (z) :=
∂f (z)
= fi (z) ≥ 0
∂zi
⇒ Maß für die absolute Stärke der Outputveränderung durch
Änderung (allein) des Faktors i um eine Einheit
Bei industriellen Prozessen häufig (Teil-)Limitationalität
⇒ Steigerung eines einzigen Produktionsfaktors bringt oft keine
Outputsteigerung
p
g
g
Seite 17
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
„Gesetz der abnehmenden Grenzproduktivität“:
(i) fi(z)
( ) ≥ 0 und
nd (ii) fii(z)
( )<0
(6 8)
(6.8)
⇒ Steigerung des i-ten Inputs bringt Steigerung des Outputs; diese fällt
aber immer kleiner aus, je mehr vom i-ten Input schon eingesetzt ist.
⇒ formale Analogie
g zum 1. Gossenschen Gesetz!
Seite 18
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Beispiel:
Empirische Produktionsfunktion aus der Agrarwirtschaft:
Getreideerträge in Abhängigkeit vom
om Stickstoff-Einsatz:
Stickstoff Einsat
Quelle: Wagner, P.:
Überlegungen
zur
Modellierung
von
Produktionsfunktionen. Unter: s4.landw.uni-halle.de/lb/publikationen/
modvpf/modvpf.htm
Seite 19
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
„Ertragsgesetz“:
g g
fi nimmt bei partieller Faktorvermehrung zunächst zu, nimmt aber von
einer gewissen Stelle z i an wieder ab (und wird eventuell sogar
negativ)
negativ).
Grafisch: S-förmiger Verlauf
f(...,zi,...)
0
Wendepunkt bei z i
zi
zi
Seite 20
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Maß für die relative Stärke der Outputveränderung durch eine
Faktorveränderung:
Produktionselastizität des Faktors i =
z
= ε y; zi (z) := f i ( z) i
f (z)
g
mit der üblichen Bedeutung
Seite 21
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Beispiel:
Cobb-Douglas-PF
Cobb
Do glas PF (CD-PF)
(CD PF) für nur
n r zwei
ei Produktionsfaktoren
Prod ktionsfaktoren (s.
(s 3.
3
Beispiel oben):
y = f ( z1 , z 2 ) = cz1α z 2β
mit c, α, β > 0, konst., und 0 < α , β < 1.
⇒
α −1
f1 ( z) = cαz1
β
z2 > 0
f11 ( z) = cα(α − 1) z1α − 2 z 2β < 0
α
β −1
,
f 2 (z) = cβz1 z 2
>0
,
f 22 (z) = cβ(β − 1) z1α z 2β − 2 < 0
⇒ f genügt dem „Gesetz der abnehmenden Grenzproduktivitäten“, nicht
jedoch dem „Ertragsgesetz“.
Seite 22
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Grafische Darstellung der CD
CD-Produktionsfunktion
Produktionsfunktion für zwei Inputs A und K:
Seite 23
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Produktionselastizitäten:
α −1
β
z1
cαz1 z 2 z1
ε f ; z1 (z1 , z 2 ) = f1 (z1, z 2 )
=
=α
α β
f (z1 , z 2 )
cz1 z 2
(6.10.1)
εf ; z 2 ( z1 , z 2 ) = β
(6.10.2)
und analog
Auswirkungen
von
gleichzeitigen
Änderungen
Produktionsfaktoren („totale Faktorvariation“)
aller
Erhöhung aller Produktionsfaktoren um denselben Prozentsatz (=
proportionale Faktorvariation):
statt z = (z1,...,zi,...,zm) der Inputvektor
t ⋅ z = ( tz1 ,..., tz i ,..., tz m ) = t ⋅ ( z1 ,..., z i ,...z m )
Seite 24
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Bezeichnungen:
Steigende
g
Skalenerträge:
g
⇔ f ( t ⋅ z) > t ⋅ f (z)
Konstante Skalenerträge:
⇔ f ( t ⋅ z) = t ⋅ f (z)
(6.11)
Abnehmende Skalenerträge: ⇔ f ( t ⋅ z) < t ⋅ f (z)
jeweils für alle t > 0
Steigende Skalenerträge: „10% mehr rein (als Inputs) ⇒ mehr als 10%
zusätzlich raus (als Output)“
Seite 25
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
PF f heißt homogen vom Grad h, falls
f ( t ⋅ z) = t h ⋅ f (z) für alle z =(z1,...,zi,...,zm) > 0 alle t > 0
f linear homogen :⇔ f ( t ⋅ z) = t ⋅ f (z) für alle z und t > 0
Beispiel:
Für die obige CD-PF
y = f (z1 , z 2 ) = cz1α z 2β
α
ist
β
f ( tz1 , tz 2 ) = c( tz1 )α ( tz 2 )β = t α +βcz1 z 2 = t α + βf (z1 , z 2 )
⇒ Die CD-PF f ist homogen vom Grad h = α + β
Falls α + β = 1 ist,, ist die CD-PF linear homogen.
g
(6.12)
(6 13)
(6.13)
Seite 26
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Isoquanten eines Unternehmens:
Menge
g
aller Faktoreinsatzpaare
p
((z1,z2)),
Outputmenge hergestellt werden kann.
mit
denen
Grafisch für m = 2:
z2
0
f(z1,z2) = konst.
z1
dieselbe
Seite 27
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Grenzrate der technischen Substitution zwischen Faktor i und
Faktor j (marginal rate of technical substitution, MRTSi,j):
MRTSi,j(z1,...,zi,...,zj,...,zn) = MRTSi,j(z) =
=
∂f (z) ∂f(z) f j ( z)
:
=
∂zi
∂z j
fi (z)
∆f
∆z
∆z
≈ i ≈ j ≈ −Steigung der Isoquante
∆f
∆zi
∆z j
(6.14)
Sie gibt an, wieviele Einheiten von Faktor j benötigt werden, um eine
Einheit von Faktor i zu ersetzen.
ersetzen
Seite 28
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Vor allem im makroökonomischen Bereich von Bedeutung:
Bei makroökonomischer CD-PF
BIPt = F(A, K , t ) = ceλt A α K β
(6.15)
FA cαA α −1K βeλt α K
MRTSA; K (A, K ) =
=
=
α β −1
FK
βA
cβA K
(6.16)
ist:
d.h. eine Arbeitsstunde lässt sich (wenn K der aktuelle Kapitaleinsatz
und A der aktuelle Arbeitseinsatz ist) durch
αK
βA
Einheiten Kapital ersetzen.
Seite 29
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Kosten K(y) zur Produktion des Outputs y:
aus Einkauf/Bezahlung
g der einzelnen Produktionsfaktoren zi
(vereinfachte Sicht!)
⇒
m
K ( y) = ∑ w i z i
i =1
mit wi = Preis von Input i
Verhaltensannahme:
Unternehmen versuchen, kostenminimale Inputs zu verwenden.
⇒
Seite 30
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Kostenminimierungsproblem der Unternehmung:
Gesucht:
Zu
vorgegebenem (gewinnmaximalem) Output y diejenigen
Inputmengen z1*, ... , zm* die Lösung des Problems (K1) sind:
m
K ( y) = ∑ w i zi → min .
i =1
unter der (technischen) Nebenbedingung
(K1)
y = f (z1 ,..., z m )
Notwendige Bedingungen für die kostenminimalen Faktormengen
(aus Lagrangeansatz wie in der Nachfragetheorie!):
*
*
f i (z1 ,..., z m ) w i
=
*
*
f k (z1 ,..., z m ) w k
((6.17))
Seite 31
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Lösungen zi* von (K1) sind Funktionen des Outputs y (und der
Faktorpreise):
zi* = zi*(y)
⇒ (Minimal-)Kostenfunktion des Unternehmens:
m
K ( y ) = ∑ w i z i* ( y )
(6.18)
i =1
Weitere Begrifflichkeiten:
Durchschnittskosten (average cost (AC)) =
Grenzkosten (marginal cost (MC)) =
K ( y)
y
(6.19)
dK ( y)
= K
K’(y)
(y) =: MC(y) (6.20)
(6 20)
dy
Seite 32
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Zusammenhang zwischen Durchschnitts- und Grenzkosten:
Grenzkostenkurve
geht
g
durch
Durchschnittskostenkurve:
das
Minimum
⎛ K ( y) ⎞
d⎜
y ⎠ yK' ( y) − K ( y)
dAC( y)
= ⎝
0=
=
dy
dy
y2
⇔ y * K ' ( y*) = K ( y*) ⇔ K ' ( y*) =
K ( y*)
⇔ MC( y*) = AC( y*)
y*
der
Seite 33
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Grafisch:
AC(y), MC(y)
MC
AC
0
y*
y
Seite 34
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Unterschied zwischen kurzfristiger und langfristiger Kostenkurve:
Aus technischen, organisatorischen und rechtlichen Gründen:
Kurzfristig nicht alle Inputs veränderbar.
⇒ kurzfristige Kostenfunktion Kkurzfr hat anderen Verlauf als
langfristige Kostenfunktion Klangfr
Beispiel:
2. Produktionsfaktor kurzfristig auf dem Wert z 2 eingefroren.
⇒ Kostenminimierungsproblem eingeschränkt:
Seite 35
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
K kurzfr ( y) =: K z ( y) =
2
min
{
( w1z1 + w 2 z 2 )
((6.21))
z1
mit y = f ( z1 , z 2 )
⇒ Minimum hat i.A. einen größeren Wert als ohne diese Einschränkung
⇒
K kurzfr ( y) ≥ K langfr ( y)
(6.22)
⇒ gilt auch für die entsprechenden Durchschnittskosten:
K kurzfr ( y) K langfr ( y)
SAC( y) :=
≥
=: LAC( y)
y
y
(6 23)
(6.23)
Seite 36
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Aus sukzessiven Produktionsausweitungen hervorgehende langfristige
Durchschnittskurvenkurve LAC ist „Einhüllende“ der zugehörigen
kurzfristigen Durchschnittskostenkurven SACi :
AC
SACi
LAC
SAC3
SAC2
0
y
Seite 37
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Zusammenhang
zwischen
kurzund
Grenzkostenkurve, d.h. zwischen SMC und LMC:
langfristiger
Im Betriebsoptimum y* beide gleich.
Bei Steigerung über y* hinaus:
Bestimmte Produktionsfaktoren können nicht kostenminimal erhöht
werden:
Überstundentarife,
Fehlen
günstiger,
geeigneter
Arbeitskräfte, Beschaffung bei teureren Lieferanten
MC
SMC
0
LMC
y
Seite 38
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
In kurzfristiger Sichtweise zu unterscheiden:
Fixe Kosten: Kosten, die unabhängig
g g von der Outputmenge
p
g sind,
also Kosten, die (auch) beim Output y = 0 anfallen; d.h.
f
Fixe Kosten = K(0) =: K
(6.24)
variablen Kosten: die outputabhängigen
A = y 2 Kosten:
f
Variable Kosten := K(y) - K =: K v = K v ( y )
(6.25)
Also:
Gesamtkosten = fixe Kosten + variable Kosten
K( y) = K v ( y) + K f
(6.26)
Seite 39
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Typische fixe Kosten:
Mieten, Abschreibungen,
g
Darlehen und Anleihen
bestimmte
Personalkosten,
Zinsen
Beispiel (Wiese (2005),
(2005) S.221):
S 221):
Produktion eines Gutes aus Arbeit A und Kapital K
Fixer Kapitaleinsatz von K0 = 1000
dafür fester Zinssatz von 5%
Variabler Arbeitseinsatz A
Produktionsfunktion (PF) bei festem Kapitaleinsatz K0 = 1000:
y = F( K , A ) = A
für
Seite 40
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Preis für Arbeit (= Kosten pro Arbeitsstunde): q A = 20 €/ h
Zur Produktion von y sind
A = y2
Stunden einzusetzen.
Einsatz von Kapital: immer K = K0 = 1000
K s ( y) = q A y 2 + 1000 ⋅ 0,05 = 20y 2 + 50
⇒ kurzfristige Kosten zur Produktion von y:
für y = 0
⎧0
K ( y) = ⎨
⎩ 4yy + 10 für y > 0
⇒
K f = 50
und
K v ( y ) = 20 y 2
Seite 41
Stehling | AVWL 3 (Mikro) | SS 08
- Kap. 7: Grundlagen der Produktions- und Kostentheorie
Auch bei variablen Kosten u.U. Bestandteile, die sich auch langfristig
nicht reduzieren lassen und erst auf 0 zurückgehen, wenn die
Produktion g
gänzlich eingestellt
g
wird.
Quasi-fixe Kosten
Beispiel: Gebäudeheizung
für y = 0
⎧0
K( y) = ⎨
⎩ 4y + 10 für y > 0
⇒ quasi-fixe Kosten von 10