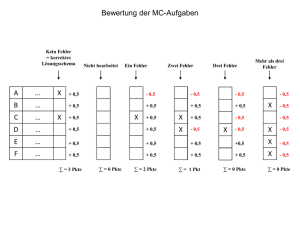
Die Slutsky

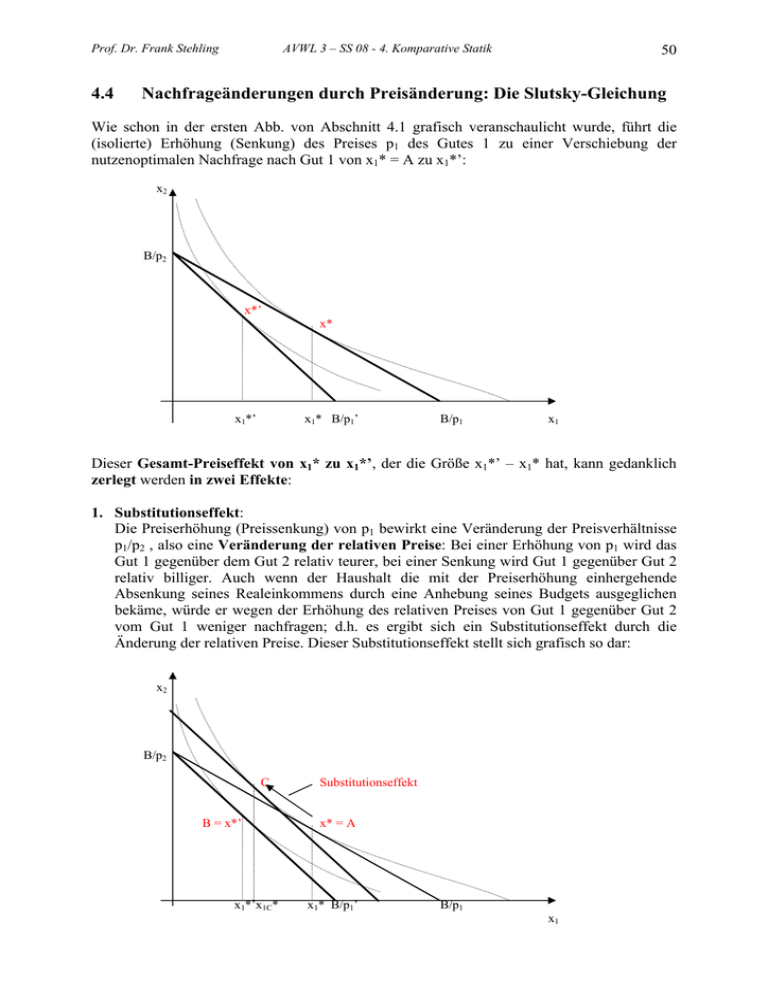
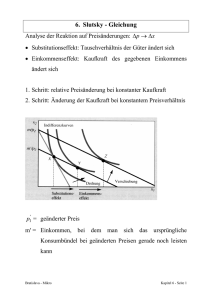
Prof. Dr. Frank Stehling
4.4
AVWL 3 – SS 08 - 4. Komparative Statik
50
Nachfrageänderungen durch Preisänderung: Die Slutsky-Gleichung
Wie schon in der ersten Abb. von Abschnitt 4.1 grafisch veranschaulicht wurde, führt die
(isolierte) Erhöhung (Senkung) des Preises p1 des Gutes 1 zu einer Verschiebung der
nutzenoptimalen Nachfrage nach Gut 1 von x1* = A zu x1*’:
x2
B/p2
x*’
x*
x1*’
x1* B/p1’
B/p1
x1
Dieser Gesamt-Preiseffekt von x1* zu x1*’, der die Größe x1*’ – x1* hat, kann gedanklich
zerlegt werden in zwei Effekte:
1. Substitutionseffekt:
Die Preiserhöhung (Preissenkung) von p1 bewirkt eine Veränderung der Preisverhältnisse
p1/p2 , also eine Veränderung der relativen Preise: Bei einer Erhöhung von p1 wird das
Gut 1 gegenüber dem Gut 2 relativ teurer, bei einer Senkung wird Gut 1 gegenüber Gut 2
relativ billiger. Auch wenn der Haushalt die mit der Preiserhöhung einhergehende
Absenkung seines Realeinkommens durch eine Anhebung seines Budgets ausgeglichen
bekäme, würde er wegen der Erhöhung des relativen Preises von Gut 1 gegenüber Gut 2
vom Gut 1 weniger nachfragen; d.h. es ergibt sich ein Substitutionseffekt durch die
Änderung der relativen Preise. Dieser Substitutionseffekt stellt sich grafisch so dar:
x2
B/p2
C
B = x*’
x1*’x1C*
Substitutionseffekt
x* = A
x1* B/p1’
B/p1
x1
Prof. Dr. Frank Stehling
AVWL 3 – SS 08 - 4. Komparative Statik
51
Das Nutzenoptimum bei Ausgleich der Realeinkommenseinbuße und mit dem neuen
relativen Preis p1’/p2 liegt im Punkt C; es ist also gegeben durch das Optimum, das der
Haushalt bei diesem neuen Preisverhältnis auf der alten Isonutzenlinie erreichen kann.
Der Substitutionseffekt ist also gegeben durch die Differenz
x1C* - x1* < 0
(Substitutionseffekt)
2. Einkommenseffekt:
Die Preiserhöhung (Preissenkung) bewirkt eine Veränderung der Konsummöglichkeiten
durch die Veränderung des Realeinkommens: Eine Preiserhöhung von p1 bewirkt (bei
konstantem Budget B und konstantem Preis p2) eine Einschränkung der
Konsummöglichkeiten, eine Preissenkung eine Erweiterung der Konsummöglichkeiten.
Dieser (reine) Einkommenseffekt entspricht grafisch der Bewegung von C zu D in der
obigen Abbildung:
x2
B/p2
C
Substitutionseffekt
D = x*’
x* = A
x1*’x1C*
x1* B/p1’
B/p1
x1
Einkommenseffekt
Bei Konstanthalten des (neuen) relativen Preises wird das Budget (gedanklich) wieder
auf das Niveau B abgesenkt, so dass der Optimalpunkt x*’ = D erreicht wird. Die Höhe
des (reinen) Einkommenseffekts (bezogen auf Gut 1) ist damit die Differenz
x1*’ - x1C*
(Einkommenseffekt)
Er ist in diesem Fall negativ.
Der Gesamteffekt der Preisveränderung von Gut 1 lässt sich damit aufsplitten in die
Summe von Substitutions- und Einkommenseffekt:
Gesamteffekt =
x1*’ – x1* = (x1C* - x1*)
= Substitutionseffekt
+
(x1*’ - x1C*) =
+
Einkommenseffekt
Prof. Dr. Frank Stehling
AVWL 3 – SS 08 - 4. Komparative Statik
52
Grafisch:
x2
B/p2
C
Substitutionseffekt
D = x*’
x* = A
x1*’x1C*
Einkommenseffekt
x1* B/p1’
B/p1
x1
Gesamteffekt
Die sogenannten Slutsky-Gleichungen drücken diesen Sachverhalt analytisch aus (sie sind
nach E. Slutsky (russ. Mathematiker, Statistiker und Ökonom; 1880 - 1948) benannt, der
diesen Sachverhalt als erster systematisch untersucht und diese Gleichungen abgeleitet hat.
Zu ihrer Ableitung (hier nur für den Fall zweier Güter) erinnern wir uns (s. 3. Kap.), dass die
(Marshallschen) Nachfragefunktionen die Abhängigkeit der Nachfrage nach Gut i im
Haushaltsoptimum von den Preisen p1 und p2 sowie dem Budget B angeben. Für das Gut 1 ist
also:
x1* = n1(p1,p2,B)
Dabei ist also x1*
Optimierungsproblems
(zusammen
mit
dem
entsprechenden
u(x1,x2) → max.
unter der Nebenbedingung
p1x1 + p2x2 = B
x2*)
Lösung
des
(P1)
wobei wir wie früher voraussetzen wollen, dass die Nutzenfunktion u streng monoton
wachsend und streng konkav ist. Die Optimalwerte x1* und x2* von (P1) sind dann
eindeutig bestimmt.
Im Unterschied dazu gibt die kompensierte (also Hickssche) Nachfragefunktion nach Gut 1
die Abhängigkeit der Nachfrage nach Gut 1, die bei minimaler Gesamtausgabe das
Nutzenniveau u sichert, von eben diesem Nutzenniveau u und den geltenden Preisen p1
und p2 an:
x1** = n1komp (p1, p2, u ),
Prof. Dr. Frank Stehling
AVWL 3 – SS 08 - 4. Komparative Statik
wobei also x1** (zusammen
Optimierungsproblems
mit
dem
entsprechenden
53
x2**)
Lösung
p1x1 + p2x2 → min.
unter der Nebenbedingung
u(x1,x2) = u
des
(P2)
ist.
Wählt man nun als u in (P2) das Nutzenoptimum u* von (P1), so muss die kompensierte
Nachfrage x1** gerade gleich der nutzenmaximalen Nachfragemenge x1* aus (P1) sein, d.h.
es ist
x1* = n1(p1,p2,B) = x1** = n1komp(p1,p2,u*)
(4.13)
Angenommen nämlich, es wäre x1* ≠ x1**, so wäre das Nutzenniveau u* beim Preissystem
p1, p2 erreichbar mit der minimalen Ausgabe Bmin . Für diese müsste dann definitionsgemäß
gelten:
B ≥ Bmin = p1x1** + p2x2** ,
denn auch mit dem Budget B wird das Nutzenniveau u* beim Preissystem p1, p2 erreicht (und
zwar mit x1* und x2*).
Wäre nun sogar B > Bmin , so bedeutete dies, dass u* auch mit einem geringeren Budget als B
erreichbar wäre (nämlich mit Bmin). Das kann aber nicht sein, weil die Nutzenfunktion u als
streng monoton wachsend vorausgesetzt wurde und u* ja gerade der mit B maximal
erreichbare Nutzen (bei den Preisen p1 und p2) ist. Also muss
B = Bmin
sein.
Dann muss aber auch x1* = x1** (und x2* = x2**) sein, denn x1* und x2* sind (wegen der
strengen Konkavität der Nutzenfunktion u) die eindeutigen Lösungen von (P1).
Also gilt tatsächlich (4.13).
Setzt man in (4.13) nun B = p1x1* + p2x2* ein, so erhält man die Gleichung
n1(p1,p2, p1x1* + p2x2*) = n1komp(p1,p2, u*)
Differenziert man diese Gleichung partiell nach p1, so liefert dies mit der Kettenregel
∂n1 (p1 , p 2 , B) ∂n1 (p1 , p 2 , B)
∂n komp (p1 , p 2 , u*)
+
⋅ x1* = 1
∂p1
∂B
∂p1
oder
(4.14)
Prof. Dr. Frank Stehling
AVWL 3 – SS 08 - 4. Komparative Statik
∂n1 (p1 , p 2 , B) ∂n1komp (p1 , p 2 , u*) ∂n1 (p1 , p 2 , B)
=
−
⋅ x1 *
∂p1
∂p1
∂B
54
(4.15)
Diese Slutsky-Gleichung (4.15) besagt:
Die Änderung der Nachfrage nach Gut 1 durch eine Preisänderung dieses Gutes setzt sich
zusammen aus der Änderung der Nachfrage nach diesem Gut auf Veränderung nur von dessen
Preis hin bei konstant gehaltenem Nutzenniveau u* (d.i. also der Substitutionseffekt) und
der Nachfrageänderung durch die Realeinkommensveränderung (Einkommenseffekt).
Beispiel:
Für die Cobb-Douglas-Nutzenfunktion u ( x1 , x 2 ) = x1α x12− α mit 0<α<1 hatten wir im 3.
Kap. die Nachfragefunktionen
n1 (p1 , p 2 , B) = α
B
p1
(4.16)
und
n 2 (p1 , p 2 , B) = (1 − α)
B
p2
ermittelt (Hinweis: Setze in dem Beispiel von S. 33: β = 1 - α und γ = 0).
Ferner hatten wir ebenfalls im 3. Kap. die zugehörigen kompensierten Nachfragefunktionen
ermittelt als:
1− α
⎛ α ⎞
n1komp (p1 , p 2 , u ) = ⎜
⎟
⎝1− α ⎠
1− α
⎛p ⎞
⋅ u ⋅ ⎜⎜ 2 ⎟⎟
⎝ p1 ⎠
und
α
n
komp
2
⎛p ⎞
⎛1− α ⎞
(p1 , p 2 , u) = ⎜
⎟ ⋅ u ⋅ ⎜⎜ 1 ⎟⎟
⎝ α ⎠
⎝ p2 ⎠
α
Aus (4.16) erhält man damit den Gesamt-Preiseffekt als
∂n1
= −αB(p1 ) − 2
∂p1
Der Einkommenseffekt ist (ebenfalls aus (4.16)):
∂n1
x *
x1* = α 1 = α αB = α 2 B(p1 ) − 2 > 0
∂B
p1
( p1 ) 2
(4.17)
Prof. Dr. Frank Stehling
AVWL 3 – SS 08 - 4. Komparative Statik
und der Substitutionseffekt (aus (4.17) mit u* = ( x1*) α ( x 2 *)1− α = (α
55
B α
B
) ((1 − α) )1− α
p1
p2
wegen (4.16) und nach einigen Umformungen)):
∂n1komp
α 1− α
=(
)
u * (p 2 )1− α (α − 1)(p1 ) α − 2 = −α(1 − α)B(p1 ) − 2
∂p1
1− α
Hieraus lässt sich einfach verifizieren, dass der Gesamt-Preiseffekt tatsächlich gleich der
Summe aus Einkommens- und Substitutionseffekt ist, wie die Slutsky-Gleichung aussagt.
Die Slutsky-Gleichung lässt sich auch für den Fall von irgend n Gütern verallgemeinern, auch
für Nachfrageveränderungen eines Gutes i infolge von Preisänderungen eines anderen Gutes
k.