3.3 Slutsky-Gleichung und Marshall`sche versus Hicks`sche Nachfrage

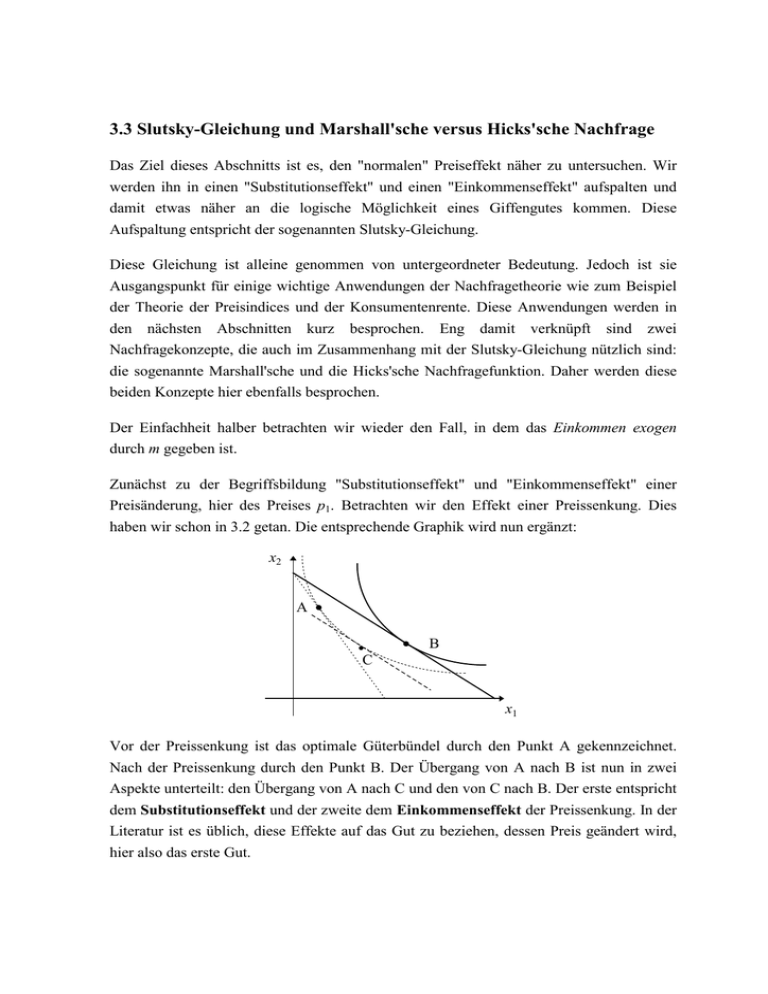
3.3 Slutsky-Gleichung und Marshall'sche versus Hicks'sche Nachfrage
Das Ziel dieses Abschnitts ist es, den "normalen" Preiseffekt näher zu untersuchen. Wir
werden ihn in einen "Substitutionseffekt" und einen "Einkommenseffekt" aufspalten und
damit etwas näher an die logische Möglichkeit eines Giffengutes kommen. Diese
Aufspaltung entspricht der sogenannten Slutsky-Gleichung.
Diese Gleichung ist alleine genommen von untergeordneter Bedeutung. Jedoch ist sie
Ausgangspunkt für einige wichtige Anwendungen der Nachfragetheorie wie zum Beispiel
der Theorie der Preisindices und der Konsumentenrente. Diese Anwendungen werden in
den nächsten Abschnitten kurz besprochen. Eng damit verknüpft sind zwei
Nachfragekonzepte, die auch im Zusammenhang mit der Slutsky-Gleichung nützlich sind:
die sogenannte Marshall'sche und die Hicks'sche Nachfragefunktion. Daher werden diese
beiden Konzepte hier ebenfalls besprochen.
Der Einfachheit halber betrachten wir wieder den Fall, in dem das Einkommen exogen
durch m gegeben ist.
Zunächst zu der Begriffsbildung "Substitutionseffekt" und "Einkommenseffekt" einer
Preisänderung, hier des Preises p1. Betrachten wir den Effekt einer Preissenkung. Dies
haben wir schon in 3.2 getan. Die entsprechende Graphik wird nun ergänzt:
x2
A •
•
•
B
C
x1
Vor der Preissenkung ist das optimale Güterbündel durch den Punkt A gekennzeichnet.
Nach der Preissenkung durch den Punkt B. Der Übergang von A nach B ist nun in zwei
Aspekte unterteilt: den Übergang von A nach C und den von C nach B. Der erste entspricht
dem Substitutionseffekt und der zweite dem Einkommenseffekt der Preissenkung. In der
Literatur ist es üblich, diese Effekte auf das Gut zu beziehen, dessen Preis geändert wird,
hier also das erste Gut.
Warum der Übergang von x1C nach x1B Einkommenseffekt der Preissenkung genannt wird,
sollte nach der Diskussion in 3.1 klar sein. Der geringere Preis des ersten Gutes entspricht
einer gewissen Einkommensverbesserung, die in der Situation, die in der Graphik
abgebildet ist, zu einer Ausweitung des Konsums vom ersten Gut führt. Der
Einkommenseffekt ist hier also als positiv vorausgesetzt. In der Graphik ist demnach
angenommen, daß das erste Gut ein normales Gut ist.
Der Substitutionseffekt "entwickelt" sich entlang einer Indifferenzlinie. Wie wir in Kapitel
2 gesehen haben, bezieht sich der Begriff der Substitution ebenfalls auf eine
Indifferenzlinie. Durch den niedrigeren Preis des ersten Gutes ist der Konsument nun
willens, einen Minderkonsum des zweiten Gutes durch den Mehrkonsum, x1C - x1A, des
ersten Gutes zu substituieren (auch, wenn ihm soviel Enkommen abgenommen wird, daß er
bei den neuen Preisen wieder auf seiner alten "niedrigeren" Indifferenzkurve landet).
Deshalb heißt der Übergang von x1A nach x1C Substitutionseffekt.
Beachten Sie, daß es mehrere Definitionen von "Substitutionseffekten" gibt. Der hier
verwendete ist der sogenannte Hicks'sche Substitutionseffekt (vgl. V8.8). Der Grund für
die hier verwendete Form liegt in einer speziellen Darstellungsform der Slutsky-Gleichung,
auf die wir später in der Vorlesung Bezug nehmen. Es soll jedoch nicht verschwiegen
werden, daß dieser Zugang nicht so transparent ist wie derjenige, der schwerpunktmäßig
von Varian gewählt wird (V8.1-8.5). Die dort dargestellte Herleitung der SlutskyGleichung sollte auf jeden Fall nachvollzogen und verstanden werden!
Dieser Substitutionseffekt wird bei einer Preissenkung immer zu einer Ausweitung des
Konsums des entsprechenden Gutes führen. Machen Sie sich dies mit Hilfe der Graphik
klar! Einen formalen Beweis finden Sie in Varian (V8.8). Entsprechend umgekehrt bei
Preiserhöhungen. Weil man das Vorzeichen des Effektes i.d.R. auf eine Preiserhöhung
bezieht, ist der Substitutionseffekt immer negativ oder Null.
Insgesamt haben wir also bei einem Preiseffekt:
x1B − x1A =
x1C − x1A
+
x1B − x1C
1
424
3
1
424
3
1
424
3
Gesamteffekt Substitutionseffekt Einkommenseffekt
Bei der betrachteten Preissenkung haben wir die folgenden Vorzeichen der einzelnen
Effekte: Der Substitutionseffekt der Preissenkung ist positiv und der Einkommenseffekt ist
positiv, wenn das erste Gut ein normales Gut ist.
Bei einer Preiserhöhung haben wir die folgenden Vorzeichen der einzelnen Effekte: Der
Substitutionseffekt der Preiserhöhung ist negativ und der Einkommenseffekt ist insgesamt
negativ, wenn das erste Gut ein normales Gut ist (höherer Preis ergibt implizit weniger
Einkommen).
Daraus können wir den Schluß ziehen, daß ein Gut nur ein Giffengut sein kann, wenn es
ein inferiores Gut ist. Denn sonst wirken Substitutionseffekt und Einkommenseffekt immer
in dieselbe Richtung und ein gestiegener Preis impliziert eine geringere Nachfrage eines
bestimmten Gutes. Außerdem ist ein Gut natürlich nicht in jedem Fall ein Giffengut, wenn
es ein inferiores Gut ist. Erst, wenn das Gut ein inferiores Gut ist und der
Einkommenseffekt den Substitutionseffekt dominiert, ist das Gut ein Giffengut.
Wie schon erwähnt entspricht die obige Zerlegung des Gesamteffektes einer Preisänderung
der Slutsky-Gleichung. Dies gilt zunächst approximativ, weil Slutsky eine andere
Definition von Substitutionseffekt benutzte. Dies ändert jedoch nichts Grundsätzliches.
Wir werden nun auf die verschiedenen Nachfragekonzepte eingehen und damit eine andere
Form der Slutsky-Gleichung herleiten.
Zunächst kennen wir schon die Marshall'sche Nachfragefunktion. Sie entspricht nämlich
dem Nachfragekonzept, das wir in diesem Kapitel bis jetzt genutzt haben. Sie ergibt sich
also als Lösung des Entscheidungsproblems:
max u( x ) u.d.N. p1 x1 + p2 x 2 ≤ m, x1 ≥ 0, x 2 ≥ 0 .
x
Für spätere Bedürfnisse definieren wir an dieser Stelle die sogenannte "indirekte
Nutzenfunktion". Sie ergibt sich, wenn man die Lösung des Entscheidungsproblems, also
die Marshall'sche Nachfragefunktion, in die Nutzenfunktion einsetzt:
V ( p, m ) := u ( x ( p, m )).
Kommen wir nun zum Konzept der Hicks'schen Nachfragefunktion oder
kompensierten Nachfragefunktion. Sie ergibt sich als Lösung des folgenden
Entscheidungsproblems:
min p1 x1 + p2 x 2 u.d.N. u( x ) ≥ u, x1 ≥ 0, x 2 ≥ 0
x
Diese Lösung hängt neben den Preisen von dem vorgegebenen Nutzenniveau u ab und wird
mit h ( p , u ) bezeichnet. Inhaltlich gibt sie also das Güterbündel an, das unter denen, die
das Nutzenniveau garantieren, das kostengünstigste ist. Setzt man diese Lösung in die
Ausgaben ein, so nennt man das Ergebnis Ausgabenfunktion:
e ( p , u ) := p1 h1 ( p , u ) + p2 h2 ( p , u ).
Die Ausgabenfunktion gibt also die minimalen Ausgaben an, die bei den Preisen p das
Nutzenniveau u garantieren.
Zunächst einige Kommentare zu dem letztgenannten Nachfragekonzept. Es hat den
gravierenden Nachteil, von Größen abzuhängen, die nicht beobachtbar sind, nämlich u. Es
ist daher kein Konzept, das das Nachfrageverhalten direkt einer Messung zuführen könnte.
Vielmehr ist es ein rein didaktisch hilfreiches Konzept, wie wir z.B. im Zusammenhang
mit der Theorie der Preisindices sehen werden. Darüber hinaus ist es nützlich bei der
formalen Darstellung der Slutsky-Gleichung. Diesem Punkt wenden wir uns nun zu.
Dazu sehen wir uns zunächst den Zusammenhang zwischen den beiden
Nachfragekonzepten an. Es gilt nämlich unter den Annahmen, die wir getroffen haben:
x ( p, e ( p , u )) = h ( p , u )
und
x ( p, m ) = h ( p , V ( p, m )).
Die erste Gleichung gilt aus folgenden Gründen: Gemäß der Definition der
Ausgabenfunktion, gibt e die minimalen Ausgaben an, die zur Nutzenfunktion u führen,
nämlich durch Wahl des entsprechenden h. Wenn ich nun dieses e dem Konsumenten als
Einkommen gebe, wird er bei Nutzenmaximierung genau dieses Güterbündel wählen.
Zunächst erreicht er damit das Nutzenniveau u. Ein Güterbündel, bei dem er einen
niedrigeren Nutzen erreicht, wird gemäß der Nutzenmaximierungshypothese nicht gewählt.
Wenn er aber ein Güterbündel wählen könnte, das zu einem höheren Nutzen führt, kann h
nicht das Güterbündel gewesen sein, das die Ausgaben minimiert und das geringere
Nutzenniveau u garantiert. Denn der Konsument könnte dann durch die Aufgabe von ein
wenig Konsum der Güter seine Ausgaben senken und immer noch das Nutzenniveau u
erreichen. Folglich ist das nutzenmaximierende Güterbündel bei Einkommen e das
Güterbündel h .
Völlig analog kann man die zweite Gleichung begründen. Eine weitere einleuchtende
Eigenschaft der Ausgabenfunktion ist:
∂e
( p, u) = hi ( p, u)
∂pi
Eine Erhöhung des Preises um eine marginale Einheit erhöht die Ausgaben um die Menge,
die von dem betreffenden Gut gekauft wird. (Dies läßt sich natürlich auch mathematisch
beweisen.)
Nach diesen Vorbereitungen können wir nun die Slutsky-Gleichung recht einfach formal
herleiten. Dies geschieht zunächst über den Schritt, die Gleichung
x1 ( p, e ( p , u )) = h1 ( p , u )
nach p1 abzuleiten:
∂x1
∂x
∂h
∂e
( p, e( p, u)) + 1 ( p, e( p, u))
( p , u ) = 1 ( p, u)
∂p1
∂m
∂p1
∂p1
oder
∂x1
∂h
∂x
∂e
( p, e( p, u)) = 1 ( p, u) − 1 ( p, e( p, u))
( p, u)
∂p1
∂p1
∂m
∂p1
oder
∂x1
∂h
∂x
( p, e( p, u)) = 1 ( p, u) − 1 ( p, e( p, u))h1 ( p, u)
∂p1
∂p1
∂m
oder
∂x1
∂h
∂x
( p, m) = 1 ( p,V ( p, m)) − 1 ( p, m) x1 ( p, m)
∂p1
∂p1
∂m
Dies ist die übliche Form der Slutsky-Gleichung, die ökonomisch natürlich nicht anders zu
interpretieren ist, als diejenige, die weiter oben mit viel geringerem formalen Aufwand
hergeleitet wurde. Der erste Summand auf der rechten Seite ist der Substitutionseffekt. Wir
sehen hier, daß man ihn durch die Hicks'sche Nachfragefunktion ausdrücken kann. Der
zweite Summand entspricht dem Einkommenseffekt. Wir sehen hier, daß dieser Effekt
durch diese Darstellung mit dem Einkommenseffekt aus 3.1,
∂x1
∂m , ausgedrückt werden
kann. Bei normalen Gütern ist diese Größe positiv (oder gleich Null). Bei normalen Gütern
ist die Marshall'sche Nachfragefunktion immer mindestens so steil wie die Hicks'sche
Nachfragefunktion. Für eine viel ausführlichere und deshalb einfacher zugängliche
Darstellung sei nochmals auf Varian, Kapitel 8 verwiesen.