(P/R = Lehrbuch Pindyck/Rubinfeld)

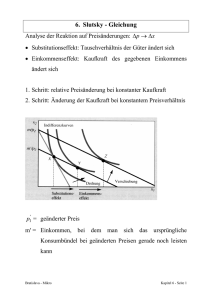
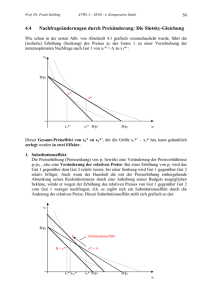
Dr. M. Ruiz HWI-B.Sc. WS9/10 Fragen zur Vorl. vom 8.01.10 Seite 1 von 3 Seiten.
Frage 97 vor Weihnachten wird in Frage 98 noch einmal wieder aufgenommen:
Frage 98 (Beispiel aus Pindyck/Rubinfeld 4.2; In der letzten Vorlesung vorgeführt).
a) Zeigen Sie, wie sich der Gesamteffekt einer Senkung des Güterpreises p2 in einen
Substitutionseffekt (bei Nutzenstabilisierung, also entlang einer gegebenen Indifferenzkurve) und
einen Einkommenseffekt zerlegen läßt. Führen Sie dazu als ersten Zwischenschritt eine fiktive
Budgetgerade ein, die bereits die Steigung des neuen Preisverhältnisses aufweist, aber noch die alte
Indifferenzkurve tangiert.
( Grafische Analyse im (x1,x2)-Diagramm mit ausführlichem Kommentar; Vgl. Vorlesung oder P/R ).
b) Diskutieren Sie die Wirkungsrichtung des Substitutionseffekts und die Wirkungsrichtung des
Einkommenseffekts der unterstellten Preissenkung bei Gut 2 auf die Nachfragemenge von Gut 2.
Welche Schlußfolgerungen lassen daraus für die Wirkungsrichtung des Gesamteffekts der
Preissenkung auf die Nachfragemenge von Gut 2 ziehen?
Zusatzfrage: Wie sehen Substitutionseffekt und Einkommenseffekt der unterstellten Preissenkung bei
Gut 2 auf die Nachfragemenge von Gut 1 aus? (Hinweis: Die Preissenkung von Gut 2 führt dazu, das
Gut 1 relativ billiger wird, obwohl Preis 1 sich nicht verändert hat. Die Preissenkung von Gut 2 löst also
einen Substitutionseffekt "über Kreuz" auf Gut 1 aus und natürlich auch einen Einkommenseffekt auf
Gut 1. Beachten Sie: Bei Überkreuzsubstitution gelten die in der Wirkungstabelle aus der Vorlesung
festgehaltenen Zusammenhänge nicht !!!!)
c) Woran würde man bei der Analyse des Substitutionseffekts und des Einkommenseffekts erkennen,
ob es sich bei dem untersuchten Gut 2 um ein Giffen-Gut handeln könnte?
d) Erklären Sie, warum jedes Giffen-Gut immer ein absolut inferiores Gut sein muß, nicht aber jedes
absolut inferiore Gut ein Giffen-Gut sein muß. (Vgl.Pindyck/Rubinfeld 4.2).
Klausur-Hinweis: Die Auswirkung der Änderung eines Güterpreises auf die Nachfragemenge kann
nach Hicks in einen Substitutionseffekt und einen Einkommenseffekt zerlegt werden. Man sollte diese
Zerlegungen unbedingt einmal für jeden denkbaren Fall von Preisänderung (zwei Preise p1 und p2,
zwei Änderungsrichtungen, Preis steigt oder Preis fällt) konstruieren, um in der Klausur auf jeden
möglichen Fall vorbereitet zu sein. (Siehe nächste Aufgabe 99) Zeichnen Sie , ausgehend vom
Ausgangsoptimum, zunächst immer den Substitutionseffekt und danach den Einkommenseffekt bis
zum End-Optimum. Zeichnen Sie dazu die fiktive Budgetgerade und den Substitutionseffekt entlang
der alten Indifferenzkurve und dann den Einkommenseffekt mit der Parallelverschiebung zur neuen
Indifferenzkurve.
Wichtiger Hinweis: Es ist nicht gestattet, die Ordinatenachse anders als mit x1 und die Abzissenachse
anders als mit x2 zu bezeichnen: Abweichungen führen zu Punktabzügen!)
Frage 99 (Frage wie 98, aber mit einer Erhöhung des Güterpreises p1 )
a) Zeigen Sie, wie sich der Gesamteffekt einer Erhöhung des Güterpreises p1 in einen
Substitutionseffekt (bei Nutzenstabilisierung, also entlang einer gegebenen Indifferenzkurve) und
einen Einkommenseffekt zerlegen läßt. Führen Sie dazu als ersten Zwischenschritt eine fiktive
Budgetgerade ein, die bereits die Steigung des neuen Preisverhältnisses aufweist, aber noch die alte
Indifferenzkurve tangiert.
( Grafische Analyse im (x1,x2)-Diagramm mit ausführlichem Kommentar).
b) Diskutieren Sie die Wirkungsrichtung des Substitutionseffekts und die Wirkungsrichtung des
Einkommenseffekts der unterstellten Preiserhöhung bei Gut 1 auf die Nachfragemenge von Gut 1.
Welche Schlußfolgerungen lassen daraus für die Wirkungsrichtung des Gesamteffekts der
Preiserhöhung auf die Nachfragemenge von Gut 1 ziehen? (Wirkungstabelle aufstellen, wie in der
Vorlesung gezeigt) (Lösungshinweis: Folie: s_e_effekt1 herunterladen.)
Zusatzfrage: Wie sehen Substitutionseffekt und Einkommenseffekt der unterstellten Preiserhöhung bei
Gut 1 auf die Nachfragemenge von Gut 2 aus? (Hinweis: Die Preiserhöhung von Gut 1 führt dazu, das
Gut zwei relativ billiger wird, obwohl Preis 2 sich nicht verändert hat. Die Preiserhöhung von Gut 1 löst
also einen Substitutionseffekt "über Kreuz" auf Gut 2 aus und natürlich auch einen Einkommenseffekt
auf Gut 2. )
c) Woran würde man bei der Analyse des Substitutionseffekts und des Einkommenseffekts erkennen,
ob es sich bei dem untersuchten Gut 1 um ein Giffen-Gut handeln könnte? (Lösungshinweis: Folie
herunterladen s_e_effekt2 ) (Ausführlicher Lösungshinweis: Zeichnen Sie in ein (x1,x2)Diagramm für einen steigenden Preis von Gut 1 das alte Gleichgewicht (Punkt A) und das neue HHGleichgewicht (Punkt C) für den Fall, daß Gut 1 ein Giffen-Gut ist. Punkt C muß dann auf der
flacheren neuen Budgetgerade links und oberhalb von Punkt A auf der alten Budgetgerade liegen.
Nun zeichnen Sie den Punkt B ein, der auf der ursprünglichen Indifferenzkurve beim neuen
Preisverhältnis liegt. Punkt B liegt damit rechts und unterhalb von Punkt A auf einer gemeinsamen
Indifferenzkurve. Damit es zum Giffen-Paradox kommt, muss der Substitutionseffekt der
Dr. M. Ruiz HWI-B.Sc. WS9/10 Fragen zur Vorl. vom 8.01.10 Seite 2 von 3 Seiten.
Preisänderung (hier Abnahme der Nachfrage nach dem teuer gewordenen Gut 1 von Ordinatenwert
von A auf Ordinatenwert von B) durch einen entgegen gerichteten Einkommenseffekt der
Preisänderung (hier Zunahme der Nachfrage nach Gut 1 von Ordinatenwert B auf Ordinatenwert C)
überkompensiert werden. Damit der Einkommenseffekt dem
Substitutionseffekt entgegen gerichtet ist, muss die durch Preiserhöhung bewirkte Kaufkraftsenkung
(wirkt wie eine Einkommenssenkung) hier zu einer Zunahme (!!!) der Nachfragenach Gut 1 führen.
Das kann nur geschehen, wenn es sich um ein absolut inferiores Gut handelt. Daher muss jedes
Giffen-Gut immer ein absolut inferiores Gut sein. Andererseits könnte Gut 1 zwar ein absolut inferiores
Gut sein, aber der (hier positive)
Einkommenseffekt könnte absolut kleiner sein als der
(hier negative) Substitutionseffekt. Dann gäbe es keine Überkompensation, der Punkt C würde dann
zwar höher liegen als B aber doch noch niedriger als A. Man erkennt, dass nicht jedes absolut
inferiore Gut ein Giffen-Gut sein muss. Wenn die Inferiorität nicht ausgeprägt genug ist, kann auch ein
absolut inferiores Gut eine normale negative Preiselastizität der Nachfrage aufweisen.)
Frage 100
a) Ein HH isst nur Käse und Cracker und verwendet dafür sein gesamtes Budget. Erläutern Sie, ob
Käse und Cracker für den HH beide superiore Güter sein können. (Vgl. Aufgabe 94)
b) Nehmen Sie an, Käse sei für den HH ein superiores Gut, während Cracker ein absolut inferiores
Gut ist.
- Was passiert mit dem Käse-Konsum des HH, wenn der Preis für Käse fällt?
- Was geschieht gleichzeitig mit dem Cracker-Verbrauch, wenn der Preis für Käse fällt?
Begründen Sie Ihre Antworten unter Verwendung einer grafischen Analyse, in der die Gesamteffekte
der Preissenkung für Käse auf die Nachfrage nach Käse und auf die Nachfrage nach Crackern jeweils
in einen Substitutionseffekt und in einen Einkommenseffekt für Käse und einen Substitutionseffekt und
einen Einkommenseffekt für Cracker zerlegt werden!!! (Denksportaufgabe!)
********************************************************************************************************************
Für mathematisch bereits versierte Hörer: Allgemeiner formaler Hinweis zur Zerlegung der
Preisänderungswirkungen in einen Substitutionseffekt und in einen Einkommenseffekt nach Hicks
(Substitutionseffekt bei stabilem Nutzen).
Die Gesamt-Wirkung zB. von ∆p2 auf ∆x2 :
∆x2 = (∆x2subst )U konstant + (∆x2eink )p2/p1 konstant
oder mit partiellen Differentiationen:
dx2/dp2 = (dx2/dp2) U konstant
+ (dx2/de).(de/dp2)
Dabei ist der Einkommenseffekt der Preisänderung (dx2/de).(de/dp2) = (dx2/de).(-x2)
Wenn nämlich p2 zB. um genau 1 Euro steigt, sinkt die Kaufkraft des Einkommens um genau 1.x2
Also um die Anzahl der in der Ausgangssituation gekauften Güter 2. (de/dp2) = -x2 .
Durch Multiplikation der gesamten obigen Gleichung mit p2/x2 und Erweiterung des letzten Terms mit
e/e ergibt sich:
(dx2/dp2 ) (p2/x2) = (dx2/dp2) U konstant .(p2/x2) - (dx2/de).(e/x2).((p2x2)/e)
Die Preiselastizität der Nachfrage ηx2;p2 ergibt sich somit aus der Preiselastizität entlang der alten
Indifferenzkurve und der mit dem Verbrauchsanteil des Gutes gewichteten Einkommenselastizität
als:
ηx2;p2
=
ηx2;p2*U Konstant
-
((p2x2)/e).ηx2;e
Slutzky-Gleichung
Der Gesamteffekt ergibt sich aus zwei Teileffekten.
Wir betrachten im folgenden die Zerlegung der Preiswirkungen bei Nutzenstabilisierung (im üblichen
Sprachgebrauch "nach Hicks") , wobei wir jeweils zunächst den Substitutionseffekt entlang der in der
Ausgangssituation gegebenen Indifferenzkurve U0 analysieren, also bei Nutzenstabilität im
anfänglichen Nutzenniveau U0 (dies geschieht durch Verschiebung der Ausgangsbudgetgerade
entlang der gegebenen Anfangs-Indifferenzkurve in das neue Preisverhältnis) und danach den
Einkommenseffekt, der sich durch die Parallelverschiebung der fiktiven Budgetgerade in die Endlage
ergibt. Dieser Effekt wird im Lehrbuch von P/R im Kapitel 4.2 dargestellt. Im Anhang P/R zu Kapitel 4,
S.211-212 die obige Slutsky-Gleichung erläutert:
(Die im P/R dann folgende Darstellung des "Hicksschen" Substitutionseffekts ist irreführend.
Bitte weglassen!)
********************************************************************************************************************
Dr. M. Ruiz HWI-B.Sc. WS9/10 Fragen zur Vorl. vom 8.01.10 Seite 3 von 3 Seiten.
Frage 101
a) Erläutern Sie die Problematik, das gängige ordinale Nutzenkonzept (Pareto) mit einer reellen
Nutzenfunktion wie etwa einer C-D-Funktion darzustellen.
b) Was versteht man unter einer monotonen Transformation einer Nutzenfunktion, geben Sie für
U= x1x2 fünf Beispiele für monotone Transformationen an. (Zeigen Sie mit jeweils einem Beispiel,
dass die Transformationen tatsächlich monoton sind)
c) Welche beiden der vier HH aus Frage 69 haben im Sinne des ordinalen Nutzenkonzepts die gleiche
Präferenzordnung? (Erläutern Sie Ihre Untersuchungsmethode) (Lösung: HH1 und HH2)
d) Erläutern Sie das Ergebnis aus Frage 93 mit Hilfe des Begriffs der monotonen Transformationen.
Frage 102
Erläutern und begründen Sie den folgenden Ausspruch des bekannten amerikanischen
Mikroökonomen Hal R. Varian: "Wenn es das Gesetz des abnehmenden Grenznutzens (Allgemeines
Ertragsgesetz) nicht geben würde, könnte man den Nahrungsmittelbedarf für die ganze Welt in einem
Blumentopf anbauen.
Frage 103
- Was beschreibt eine Produktionsfunktion y = g(r1 , r2) genau?
- Was bedeuten dabei die verwendeten Variablen, in welchen Dimensionen werden sie jeweils
gemessen?
- Was macht den Unterschied zwischen variablen und fixen Produktionsfaktoren aus?
- Was versteht man unter einem Ertragsgebirge, und wie sieht es aus (Zeichnung)?
- Wie ermittelt man aus einem Ertragsgebirge eine Ertragskurve für den Faktor 1?
- Wie ermittelt man aus einem Ertragsgebirge eine Isoquante?
Wie verlaufen
- die Ertragskurve und die Grenzertragskurve (Grenzproduktskurve) für den Faktor 1 ? (Zeichnung und
Diskussion der Eigenschaften)
- die Ertragskurve und die Grenzertragskurve (Grenzproduktskurve) für den Faktor 2 ? (Zeichnung und
Diskussion der Eigenschaften)
- Welche Bedeutung hat eine Vergrößerung des Faktors 2 für die Ertragskurve von Faktor 1?
- Geben Sie ein praktisches Beispiel für die Gültigkeit des sog. Ertragsgesetzes!
Frage 104
In einem Unternehmen mit gegebener Maschinenausstattung produziert jeder zusätzliche Arbeiter bis
zum sechsten Arbeiter (einschließlich) eine zusätzliche Outputeinheit. Jeder weitere Arbeiter vom
siebten Arbeiter an produziert keinen zusätzlichen Output y mehr. Zeichnen Sie die Ertragskurve des
Faktors Arbeit r1, die Kurve der durchschnittlichen Arbeitsproduktivität y/r1 und die
Grenzproduktivitätskurve für Arbeit dy/dr1. (mit grafischer Herleitung)
Frage 105
a) Zeichnen Sie eine Ertragskurve für den Faktor 1 in ein (y-r1 -Diagramm) . Gehen Sie von zunächst
steigenden und später abnehmenden Ertragszuwächsen aus. (Vgl Abb. 6.1. im P/R S. 271.)
b) Entwickeln Sie die Durchschnittsproduktivitätskurve (y/r1)und die Grenzproduktivitätskurve (dy/dr1)
für den Faktor 1. (unter Verwendung einer weiteren Zeichnung)
c) In welchem r1-Bereich ist die Grenzproduktivität größer als die Durchschnittsproduktivität?
d) In welchem r1-Bereich gilt das sogenannte "Allgemeine Ertragsgesetz"?
Frage 106
Gegeben sei die Produktionsfunktion y = 1,2r10,4r20,3
(y Output; r1 und r2 Faktoreinsatzmengen)
Untersuchen Sie algebraisch, ob beide Produktionsfaktoren positive Grenzerträge aufweisen und ob
sie beide auch sinkende Grenzerträge aufweisen.
(Achtung: Dies sind zwei unterschiedliche Eigenschaften)
Erläutern Sie in diesem Zusammenhang die folgenden zwei Eigenschaften:
1. "Alle Faktoren sind unbegrenzt produktiv" ;
2. Es gilt für alle Faktoren das "Gesetz abnehmender Grenzprodukte".