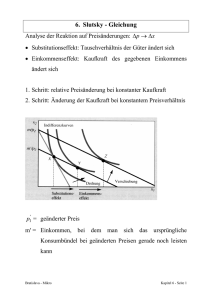
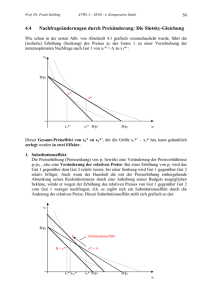
(P/R = Lehrbuch Pindyck/Rubinfeld)

Dr. M. Ruiz HWI-B.Sc. WS1011 Fragen zur Vorl. vom 13.1.11 Seite 1 von 4 Seiten.
In der heutigen Vorlesung haben wir die grafische und die algebraische Herleitung von Engel-Kurven
und von Marshall-Kurven ausführlich behandelt. Wiederholen Sie in diesem Zusammenhang die
Fragen 82, 83, 84, 85 aus V08_bscmi1011.pdf.
Frage 89
a) Die Nutzenfunktion des HH sei U = x11/8 x23/8 und das Einkommen e= 100 .
Leiten Sie die Preis-Nachfrage-Kurven (Marshall-Kurven) des HH für das Gut 1 und das Gut 2 her.
(Lösung: p1 = 25/x1 ; p2 = 75/x2 )
b) Wie groß sind hier die Preiselastizitäten der Güternachfrage in Bezug auf ihren eigenen Preis?
(Gut 1: -1 ; Gut 2: -1)
c) Bestimmen Sie die Kreuzpreiselastizitäten für Gut 1 und für Gut 2 und prüfen Sie, ob der HH die
beiden Güter eventuell als Substitute oder als Komplemente ansieht. (Güter werden als unabhängig
voneinander angesehen, denn die Kreuzpreiselastizitäten sind gleich null)
d) Untersuchen Sie, welchen Anteil seines Einkommens (p.x)/e der HH in diesem besonderen Beispiel
jeweils für Gut 1 und für Gut 2 ausgibt.
(Durch Berechnung des Optimums für beliebige Preise und Einkommenshöhen erhält man:
Gut 1:25% und Gut 2: 75% des Einkommens. Die Einkommensanteile der Güter sind in diesem
Beispiel unabhängig von der Höhe des Einkommens und unabhängig von der Höhe der Güter-Preise!)
Frage 90
Wie verlaufen die Einkommens-Konsum-Kurve und die beiden Engel-Kurven, wenn Sie bei
gegebenen Preisen p1 = 2,5 und p2 = 5 die folgenden Nutzenfunktionen unterstellen:
U = 6x10,4x20,8 ( Berechnung der Kurvengleichungen) Untersuchen Sie, ob eins der beiden Güter
inferior ist. (Lösung: f´2/f´1 = 2x1/x2 ; p2/p1 = 5/2,5 = 2 Im Optimum: ! 2x1/x2 = 2 ! x1*= x2*
x1 = e/7,5 x2 = e/7,5 Die Einkommenselastizität der Nachfrage ist in beiden Fällen gleich +1 ; es
gibt also keine inferioren Güter mit einer Einkommenselastizität zwischen Null und +1)
Frage 91 (Anwendung der Theorie des HH auf Vermögensentscheidungen unter Risiko-in der
Vorlesung behandelt)
Drei Vermögensverwalter A , B und C berücksichtigen in ihrer jeweiligen Nutzenfunktion U zum einen
den erwarteten Ertrag ew und zum anderen das Risiko s einer Anlage:
U = U(ew,s)
Aus dieser besonderen Nutzenfunktion lassen sich spezielle Indifferenzkurven für den erwarteten
Ertrag und das Risiko herleiten. Dabei geht man genau so vor, wie bei der Ermittlung der bisher
behandelten Güter-Indifferenzkurven. Statt der Analyse von Güterbündeln aus zwei Gütern werden
hier Anlagealternativen analysiert, die durch die Kombination zweier Eigenschaften gekennzeichnet
sind.
Begründen Sie: Für alle drei Anleger gilt: dU/dew > 0 und U(ew, 0) > 0 für alle ew > 0 !
(Hinweis: ew ist für alle drei Anleger ein nützliches "Gut" ).
Entwickeln und erläutern Sie in jeweils einem ew-s-Diagramm den typischen Verlauf der
Indifferenzkurven
a) für den risiko-abgeneigten Anleger A mit dU/ds < 0 (Risiko ist für A ein "Nicht-Gut")
b) für den risiko-neutralen Anleger B mit dU/ds =0
(Risiko ist für B ein "neutrales" Gut)
c) und für den risiko-freundlichen Anleger C mit dU/ds > 0 (Risiko ist für C ein nützliches "Gut")
(Hinweis: Die Steigung einer Indifferenzkurve ergibt sich aus dem Vorzeichen von
dew /ds = - (dU/ds)/(dU/dew) . Vgl. dazu Aufgabe 79d. Über die Krümmung der Indifferenzkurven
ist hier noch nichts gesagt!)
Jede Indifferenzkurve beginnt an der Ordinatenachse (s =0) bei einem bestimmten Wert ew und
verläuft mit zunehmendem s für A steigend (Risiko ist ein negatives "Gut") , für B horizontal (Risiko ist
nutzenneutral) und für C fallend (Risiko ist hat positiven Nutzen) .Bedenken Sie, daß alle Punkte auf
einer Indifferenzkurve gleichen Nutzen haben: Wenn C zb. bei gleich hohem ew einen Punkt mit
höherem s dem Punkt mit niedrigerem s vorzieht, muß dieser Punkt auf einer höheren
Indifferenzkurve liegen: dh. seine Indifferenzkurven verlaufend fallend!!! Bitte überlegen Sie genau!! )
d) Unterstellen Sie, die Anleger können bei der Anlage ihres gegebenen Vermögens V wählen
zwischen einer sicheren Anlage L mit ew = 1 und s = 0 (zb Kassenhaltung L mit sicherem Anlagewert
in Euro ) und einer sehr riskanten Anlage in ein Wertpapier W mit ew = 100 und s = 100 sowie allen
Kombinationen zwischen diesen beiden extremen Anlagen. (V = L + W)
Zeichnen Sie die lineare Portfolio-Möglichkeitskurve (Portfolio-Budgetlinie) aller durch Mischung dieser
Anlagen erreichbaren ew-s-Kombinationen für die Gesamt-Anlage in ein ew-s-Diagramm. (Hinweis: Es
handelt sich um eine Gerade durch die oben angegebenen Kombinationen mit positiver Steigung.)
A, B und C wählen jeweils ihre optimale Anlagekombination auf der Portfolio-Möglichkeitskurve mit
Dr. M. Ruiz HWI-B.Sc. WS1011 Fragen zur Vorl. vom 13.1.11 Seite 2 von 4 Seiten.
ihrem maximalen Nutzen. Wodurch unterscheiden sich die Anlagen von A, B und C? (3 Grafiken mit
Kennzeichnung des optimalen Anlagepunktes)
e) Erläutern Sie mit Hilfe der Indifferenzkurven und der Portfolio-Möglichkeitskurve (Diagramm) , wie
sich das Anlageverhalten eines leicht risikoaversen Anlegers ändert, wenn für das Wertpapier in der
Zukunft mit einem deutlich höherem ew zu rechnen ist, ohne dass sich Streuung der
Wertpapiererträge s vergrößert.
f) Schauen Sie sich die tatsächlichen Werte für Erwartungswert ("Performance") - Risiko ("Volatilität") Kombinationen in einer Grafik an, die durch eine Anlage in die wichtigsten deutschen Aktien (DAXAktien) im letzten Jahr 2010 realisierbar waren. Sie finden das ew-s-Diagramm z.B. unter
http://aktien.onvista.de/ risk-return-map : Wählen Sie: DAX, Zeitraum 52 Wochen; Darstellung absolut!
Welche DAX-Aktien hätte ein risikoaverser Anleger, im Nachhinein betrachtet, im Jahre 2010 wählen
müssen?
Frage 92
Gehen Sie von einem 2-Güter-Fall aus und nehmen Sie diesen Fall ausnahmsweise einmal
"wörtlich".
Zeigen Sie algebraisch, daß die Summe der einzelnen Einkommenselastizitäten der beiden Güter,
jeweils gewichtet mit dem relativen Anteil des betreffenden Gutes an den Gesamtausgaben, immer
gleich 1 ist.
Was bedeutet dieser Sachverhalt im 2-Güter-Fall für das Gut 2,
-wenn es sich bei dem Gut 1 um ein absolut inferiores Gut handelt?
-wenn es sich bei dem Gut1 um ein superiores Gut handelt?
(Lösungs-Hinweis: Budgetgleichung total differenzieren, wobei die Güterpreise hier konstant sind.
de = p1dx1 + p2dx2 . Dann beide Seiten durch die Einkommensänderung de teilen, sodass die linke
Seite gleich eins wird. Die Ausdrücke rechts so erweitern und anordnen, daß die
Einkommenselastizitäten und die Gewichte erkennbar werden:
1 = (dx1/de)(e/x1) . (p1x1)/e + (dx2/de)(e/x2) . (p2x2)/e
Ergebnis: Wenn Gut 1 absolut inferior ist, dann muß Gut 2 superior sein. (Fassen Sie in Worte, warum
das nach der Formel so sein muß). Das gilt aber nicht unbedingt auch umgekehrt: Wenn Gut 1
superior ist, dann kann Gut 2 relativ oder absolut inferior sein. Ob Gut 2 relativ inferior oder absolut
inferior ist, hängt von der Höhe der Einkommenselastizität von Gut 1 und von dem relativen Anteil des
Gutes 1 an den Gesamtausgaben ab: Nur, wenn das Produkt aus Einkommenselastizität von Gut 1
und Ausgabenanteil von Gut 1 (der erste Summand auf der rechten Seite) größer als eins ist, wird Gut
2 absolut inferior sein.
Achtung: Alle diese Zusammenhänge gelten nur im wörtlich gemeinten 2-Güter-Fall, wenn das
Einkommen vollständig ausgegeben wird.! Nur in diesem Fall kann man von Gut 1 auf Gut 2
schließen! Bei n>2 kann es natürlich mehrere inferiore oder mehrere superiore Güter geben)
Frage 93
a) Wie groß sind die Einkommenselastizitäten für Gut 1 und Gut 2 in Aufgabe (82b)? Wie gross sind
die Einkommenselastizitäten in Aufgabe (83b)?
b) Zeichnen Sie eine Folge von HH-Gleichgewichten für den Sonderfall, dass x1 ein absolut inferiores
Gut ist (e ist variabel. Sie zeichnen daher Punkte einer Einkommens-Konsum-Kurve)
c) Erläutern Sie, was man unter dem Sonderfall eines Giffen-Gutes versteht und zeigen Sie, wie die
Preis-Nachfrage-Kurve (Marshall-Kurve) eines Giffen-Gutes im p-x-Diagramm verläuft. Wie verläuft
die zugrunde liegende Preis-Konsum-Kurve der HH-Optimalpunkte im x1-x2-Diagramm, wenn eines
der beiden Güter ein Giffen-Gut ist?
Frage 94
Die Präferenzordnung eines HH sei beschrieben durch die Nutzenfunktion U = x11/2.x21/4 .
Die Güterpreise seien p1 = 12 und p2 = 12 .
a) Berechnen Sie die nutzenmaximalen Verbrauchsmengen für eine Konsumsumme e von
Euro 180,-. ( Hinweis: Optimalitätsbedingung aus dem Lagrange-Ansatz formulieren; Optimales
Güterkonsumverhältnis berechnen, indem man für die GRS das Verhältnis der Ableitungen
(Grenznutzen von Gut 2 zu Grenznutzen von Gut 1 bildet und gleich dem Verhältnis von Preis 2 zu
Preis 1 setzt. Die Lösung ergibt das optimale Verhältnis von x1 zu x2 .
Einsetzen des optimalen Güterverhältnisses in die Budgetgerade und Auflösen nach x1 bzw x2.
Ergebnis: x1 = 10 ; x2 = 5)
b) Wie verändern sich die Verbrauchsmengen im Haushaltsoptimum, wenn der Staat jedem
Verbraucher für Gut 2 pro Gütereinheit eine Beihilfe (Preissubvention) von Euro 6,- je ME zahlt?
Dr. M. Ruiz HWI-B.Sc. WS1011 Fragen zur Vorl. vom 13.1.11 Seite 3 von 4 Seiten.
(Hinweis: der Verbraucher zahlt jetzt also wegen der Subvention für Gut 2 nur noch p2 = 12- 6 = 6). (
Neues Optimum bei: x1 = 10 ; x2 = 10 )
c) Wie hoch ist hier der insgesamt vom Staat zu zahlende Subventionsbetrag?
( Euro 60 : Optimale Verbrauchsmenge für Gut 2 mal Subventionsbetrag 10x6=60
Achtung: Der gesamte Subventionsbetrag hängt von der tatsächlich nachgefragten Menge x2 ab!)
d) Wie würde sich die Güternachfrage im HH-Optimum verändern, wenn der Staat dem HH den
ermittelten Subventionsbetrag aus c) nicht als Preissubvention gewährt hätte, sondern ihm statt
dessen (dh bei den alten Preisen p1 = 12 und p2 = 12 ) einen gleich großen Betrag als pauschale
Einkommenshilfe (allgemeine Einkommenssubvention) zukommen lassen würde?
(Ergebnis: dann ist e = 180 + 60 = 240 und im Optimum ist x1 = 13,33 ; x2 = 6,67 )
d) Untersuchen Sie rechnerisch, welche Art der Subventionierung der HH hier vorziehen wird.
(Einsetzen der jeweiligen Lösungen in die Nutzenfunktion : Ausrechnen: U(10;10) < U(13,33 ; 6,66)
Der HH zieht die pauschale Einkommenshilfe der Preisbeihilfe vor.)
Frage 95 (Anwendung der Einkommenswirkungen und Preiswirkungen im Vergleich)
Sie haben in der Frage 94d für einen konkreten Fall rechnerisch untersucht, ob der HH eine
Preissubvention oder eine gleich große pauschale Zahlung (Einkommenssubvention) vorzieht.
Versuchen Sie in einem (x1-x2 )-Diagramm mit einer grafischen Analyse darzustellen, warum ein
beliebiger HH im allgemeinen Fall immer eine pauschale Zahlung des Subventionsbetrages einer
Preissubvention vorziehen wird. (Dabei wird natürlich unterstellt, dass der Subventionsbetrag in
beiden Fällen gleich groß ist! Vergleiche die Darstellungen in der Vorlesung)
Praktisches Beispiel: Ein HWI-Student bekommt 50% des Preises für jedes gekaufte Lehrbuch (Gut2)
von den Eltern als Preissubvention. Er kauft im 1. Semester Bücher für 500 Euro. Wie groß wäre sein
Nutzen im Vergleich, wenn er statt der Bücherbeihilfe 250 Euro zur allgemeinen Verfügung
bekommmen hätte?)
a) Leiten Sie zunächst grafisch her, wie sich der Optimalpunkt A eines HH in der Ausgangslage auf
einen neuen Optimalpunkt B nach Einführung der Preissubstitution für Gut 2 bewegt. (Der Preis für
Gut 2 wird um den Substitutionsbetrag pro Mengeneinheit des Gutes 2 reduziert). Wie groß ist der
Substitutionseffekt, der Einkommenseffekt und der Gesamteffekt der Preissubvention? (mit Grafik)
b) Konstruieren Sie danach eine neue Budgerade für den Fall, dass der HH den gleichen
Subventionsbetrag wie unter (a) statt als Preisermäßigung alternativ als Einkommenssubvention
bekommt (Einkommenserhöhung bei ursprünglichem Preisverhältnis)
(Hinweis: der optimale Punkt B unter (a) muss auch unter (b) für den HH erreichbar sein, weil der HH
sich mit der Einkommenssteigerung ja den Preis für Gut 2 "gedanklich" selber heruntersetzen kann.
Das Verständnis kann durch die folgende formale Betrachtung erhöht werden:
Steigung der Budgetgerade -p2/p1
- "Blau" A) Ausgangslage: p1x1 + p2x2 = e
Optimaler Punkt A!
p1x1 + (p2 - sp2)x2 = e
- "Grün" B) Zweckgebundene Hilfe (Preissubvention sp2 )
Optimaler Punkt B! Subventionsbetrag: sp2. *x2 = Preissubvention x Optimale Nachfragemenge von
*x2 in Punkt B. (durch * gekennzeichnet)
p1*x1 + (p2 - sp2)*x2 = e Einkommensverwendung im Optimum Punkt B.
- "Rot" C) nichtgebundene Einkommenshilfe in gleicher Höhe wie Subventionsbetrag in B!
p1x1 + p2x2 = e + sp2. *x2 !!!!! Wie man hier leicht erkennt, kann der Subventionsbetrag sp2. *x2 auf
die linke Seite gebracht werden und zur Reduktion der Ausgaben für Gut 2 eingesetzt werden.
p1x1 + p2x2 - sp2. *x2 = e
p1 *x1 + *x2(p2 - sp2 ) = e Der in B) optimale Punkt B mit (*x1,*x2) liegt also auch auf der
Budgetgerade in C. Die Budgetgeraden von B und von C haben den gemeinsamen Punkt B. (q.e.d.)
(Wird in der nächsten Vorlesung kurz erläutert)
c) Zeigen Sie, dass der Punkt B bei einer Einkommenssubstitution zwar erreichbar, aber nicht mehr
optimal ist. Konstruieren Sie den neuen Optimalpunkt C und erläutern Sie, warum dieser Punkt C bei
konvexen Indifferenzkurven immer einen höheren Nutzen haben muss als B.
( q e d !. Ein HH wird eine direkte Einkommenserhöhung ohne den Zwang zur Substitution immer
einer Preissenkung mit dem Zwang zur Substitution vorziehen, auch wenn jede Preissenkung
natürlich einen Einkommenseffekt hat. Warum bewerten die Eltern den Nutzen der Bücherbeihilfe
möglicherweise anders als der HWI-Student????) .
Dr. M. Ruiz HWI-B.Sc. WS1011 Fragen zur Vorl. vom 13.1.11 Seite 4 von 4 Seiten.
Frage 96 (Studieren Sie sorgfältig Pindyck/Rubinfeld Kap. 4.2 ).
a) Zeigen Sie, wie sich der Gesamteffekt einer Senkung des Güterpreises p2 in einen
Substitutionseffekt (bei Nutzenstabilisierung, also entlang einer gegebenen Indifferenzkurve) und
einen Einkommenseffekt zerlegen läßt. Führen Sie dazu als ersten Zwischenschritt eine fiktive
Budgetgerade ein, die bereits die Steigung des neuen Preisverhältnisses aufweist, aber noch die alte
Indifferenzkurve tangiert.
( Grafische Analyse im (x1,x2)-Diagramm mit ausführlichem Kommentar; Vgl. Vorlesung oder P/R ).
b) Diskutieren Sie die Wirkungsrichtung des Substitutionseffekts und die Wirkungsrichtung des
Einkommenseffekts der unterstellten Preissenkung bei Gut 2 auf die Nachfragemenge von Gut 2.
Welche Schlußfolgerungen lassen daraus für die Wirkungsrichtung des Gesamteffekts der
Preissenkung auf die Nachfragemenge von Gut 2 ziehen?
Zusatzfrage: Wie sehen Substitutionseffekt und Einkommenseffekt der unterstellten Preissenkung bei
Gut 2 auf die Nachfragemenge von Gut 1 aus? (Hinweis: Die Preissenkung von Gut 2 führt dazu, das
Gut 1 relativ billiger wird, obwohl Preis 1 sich nicht verändert hat. Die Preissenkung von Gut 2 löst also
einen Substitutionseffekt "über Kreuz" auf Gut 1 aus und natürlich auch einen Einkommenseffekt auf
Gut 1. Beachten Sie: Bei Überkreuzsubstitution gelten die in der Wirkungstabelle aus der Vorlesung
festgehaltenen Zusammenhänge nicht !!!!)
c) Woran würde man bei der Analyse des Substitutionseffekts und des Einkommenseffekts erkennen,
ob es sich bei dem untersuchten Gut 2 um ein Giffen-Gut handeln könnte?
d) Erklären Sie, warum jedes Giffen-Gut immer ein absolut inferiores Gut sein muß, nicht aber jedes
absolut inferiore Gut ein Giffen-Gut sein muß. (Vgl.Pindyck/Rubinfeld 4.2 ).
Frage 97
a) Ein HH isst nur Käse und Cracker und verwendet dafür sein gesamtes Budget. Erläutern Sie, ob
Käse und Cracker für den HH beide superiore Güter sein können. (Vgl. Aufgabe 94)
b) Nehmen Sie an, Käse sei für den HH ein superiores Gut, während Cracker ein absolut inferiores
Gut ist.
- Was passiert mit dem Käse-Konsum des HH, wenn der Preis für Käse fällt?
- Was geschieht gleichzeitig mit dem Cracker-Verbrauch, wenn der Preis für Käse fällt?
Begründen Sie Ihre Antworten unter Verwendung einer grafischen Analyse, in der die Gesamteffekte
der Preissenkung für Käse auf die Nachfrage nach Käse und auf die Nachfrage nach Crackern jeweils
in einen Substitutionseffekt und in einen Einkommenseffekt für Käse und einen Substitutionseffekt und
einen Einkommenseffekt für Cracker zerlegt werden!!! (Denksportaufgabe!)