xaa I 2 1 3I y - iae.uni

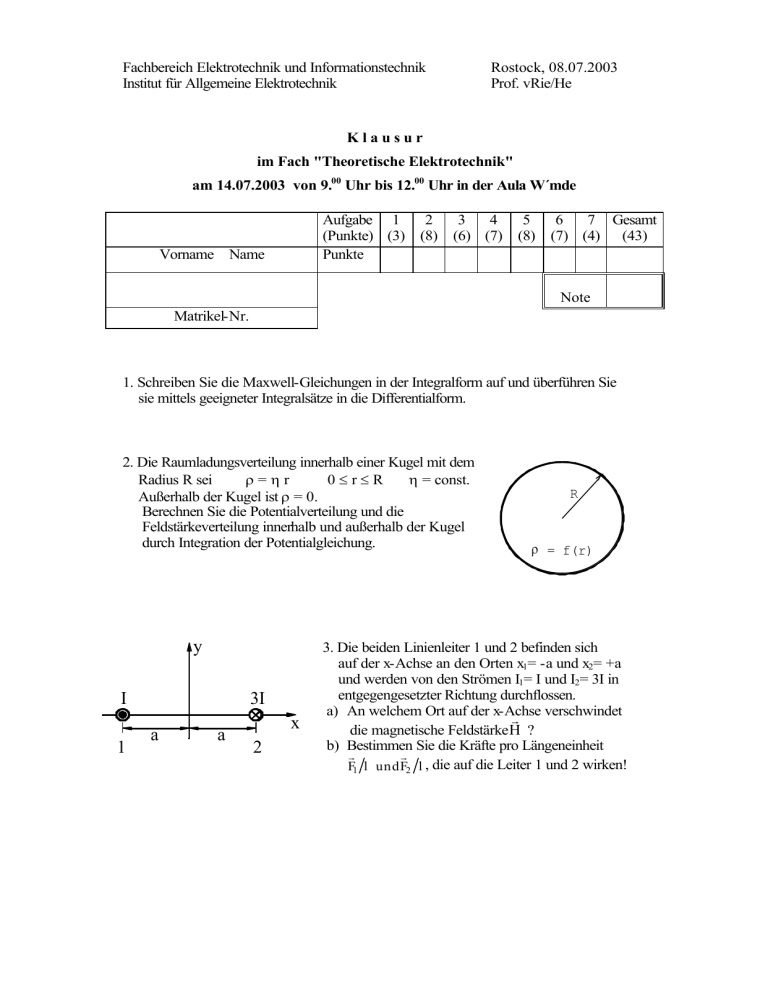
Fachbereich Elektrotechnik und Informationstechnik
Institut für Allgemeine Elektrotechnik
Rostock, 08.07.2003
Prof. vRie/He
Klausur
im Fach "Theoretische Elektrotechnik"
am 14.07.2003 von 9.00 Uhr bis 12.00 Uhr in der Aula W´mde
Aufgabe 1
2
3
4
5
6
7 Gesamt
(Punkte) (3) (8) (6) (7) (8) (7) (4) (43)
Punkte
Vorname Name
Note
Matrikel-Nr.
1. Schreiben Sie die Maxwell-Gleichungen in der Integralform auf und überführen Sie
sie mittels geeigneter Integralsätze in die Differentialform.
2. Die Raumladungsverteilung innerhalb einer Kugel mit dem
Radius R sei
ρ=ηr
0≤r≤R
η = const.
Außerhalb der Kugel ist ρ = 0.
Berechnen Sie die Potentialverteilung und die
Feldstärkeverteilung innerhalb und außerhalb der Kugel
durch Integration der Potentialgleichung.
y
I
1
3I
a
a
x
2
R
ρ = f(r)
3. Die beiden Linienleiter 1 und 2 befinden sich
auf der x-Achse an den Orten x1= -a und x2= +a
und werden von den Strömen I1= I und I2= 3I in
entgegengesetzter Richtung durchflossen.
a) An welchem Ort auf der x-Achse
verschwindet
r
die magnetische Feldstärke H ?
b) Bestimmen Sie die Kräfte pro Längeneinheit
r
r
F1 l undF2 l , die auf die Leiter 1 und 2 wirken!
4. Eine in z-Richtung verlaufende Stromquelle mit
kreisförmigem Querschnitt (Radius r) der Länge l
befindet sich im Abstand h zu einer parallel
verlaufenden Grenzfläche zwischen zwei
Medien. Berechnen Sie den Potentialverlauf ϕ(x)
durch Integration der Potentialgleichung und den
Feldstärkeverlauf E(x) entlang der x-Achse,
wenn die Stromquelle den Strom I gleichmäßig
verteilt abgibt. An welcher Stelle befindet sich ein
Feldstärkemaximum ?
y
ε1 κ1= 0
ε 2 κ2> 0
z
x
h
I
5. Eine monochromatische ebene Welle breitet sich im Vakuum mit der
Gechwindigkeit c0 =
1
in positive x – Richtung aus. Ihre magnetische
ε0 µ0
r r
Feldstärke ist gegeben durch H ( r,t ) = H 0 e (
j k0 x − ω0 t )
r
ey
mit k 0 =
ω0
.
c0
a) Zeigen Sie, daß diese Welle die homogene Wellengleichung
r r
1 ∂2 r r
∆ H ( r,t ) − 2 2 H ( r,t ) = 0 erfüllt.
c ∂t
r r
b) Bestimmen Sie die Richtung der zugehörigen elektrischen Feldstärke E ( r , t )
über die Maxwellschen Gleichungen.
6. Gegeben sei ein Rechteckhohlleiter mit ideal leitender Berandung. Im Inneren des
Hohlleiters breiten sich TE – Wellen aus. Leiten Sie die Beziehung für die
Grenzfrequenz dieser Moden aus der Separationsgleichung ab! Welches ist der
Grundmode, welche Grenzfrequenz besitzt er ? Für die Komponenten des
elektrischen Feldes der TE – Moden gilt allgemein:
E x = Acoskx x ⋅ sink y y j( ωt − kz z )
; Ez = 0 .
⋅e
E y = Bsink x x ⋅ cosk y y 
Berechnen Sie die Komponenten der magnetischen Feldstärke des Grundmodes mit
Hilfe der Maxwellschen Gleichungen!
+Q
-Q
εr(x)
A
x
0
d
7. In einem Plattenkondensator befinde sich ein
Dielektrikum mit ortsabhängiger Dielektrizitätszahl
ε r ( x ) = 1 + α x mit α = const. > 0.
Berechnen Sie die Verschiebungsflußdichte, die
elektrische Feldstärke und den Potentialverlauf im
Dielektrikum sowie die Kapazität des Kondensators.