PROBLEM DER WOCHE 4 1. In einem Quadrat ABCD sind auf zwei
Werbung
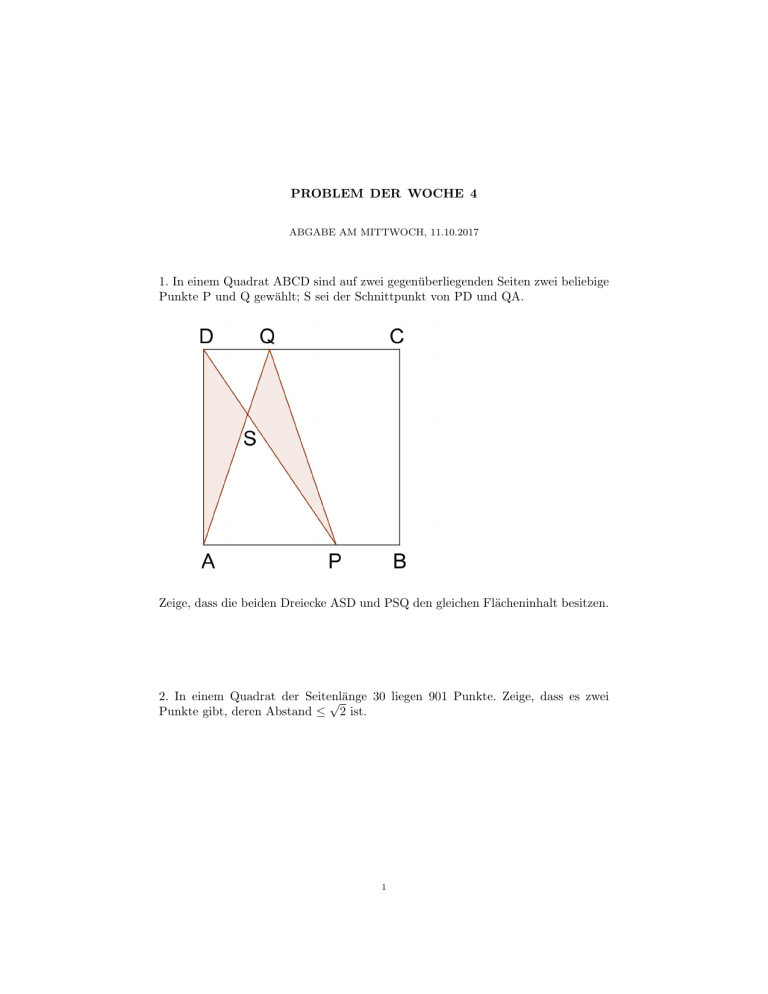
PROBLEM DER WOCHE 4 ABGABE AM MITTWOCH, 11.10.2017 1. In einem Quadrat ABCD sind auf zwei gegenüberliegenden Seiten zwei beliebige Punkte P und Q gewählt; S sei der Schnittpunkt von PD und QA. Zeige, dass die beiden Dreiecke ASD und PSQ den gleichen Flächeninhalt besitzen. 2. In einem Quadrat der Seitenlänge 30 liegen 901 Punkte. Zeige, dass es zwei √ Punkte gibt, deren Abstand ≤ 2 ist. 1 2 ABGABE AM MITTWOCH, 11.10.2017 1. Ergänzungsgleichheit Um die Gleichheit zweier Flächen zu zeigen, gibt es zwei Standardtechniken: entweder zerlegt man die beiden Flächen in Teile und zeigt, dass die Teile gleich groß sind (Zerlegungsgleichheit), oder man zeigt, dass man die Flächen aus einer größeren Fläche erhält, von der man gleich große Teile wegnimmt (Ergänzungsgleichheit). Die erste binomische Formel (a + b)2 = a2 + 2ab + b2 kann man durch Zerlegung eines Quadrats der Kantenlänge a + b veranschaulichen: Abbildung 1. Binomische Formel Auch den Satz des Pythagoras kann man durch Zerlegen eines Quadrats beweisen: Abbildung 2. Satz des Pythagoras Das linke Quadrat mit der Kantenlänge a + b ist zerlegt in ein Quadrat der Kantenlänge c und vier rechtwinklige Dreiecke mit Katheten a und b und Hypotenuse PROBLEM DER WOCHE 4 3 c. Das rechte Quadrat hat ebenfalls Kantenlänge a + b, besteht aber aus zwei Quadraten der Kantenlängen a und b, sowie ebenfalls vier rechtwinkligen Dreiecken mit Katheten a und b und Hypotenuse c. Also muss a2 + b2 = c2 gelten. Das Prinzip der Ergänzungsgleichheit steckt hinter dem Gnomonsatz, einem Spezialfall des Strahlensatzes. Ist C irgendein Punkt auf der Diagonalen AG eines Rechtecks AEGI (derselbe Beweis funktioniert allgemeiner für ein Parallelogramm), so sind die beiden dadurch definierten Rechtecke BEFC und CDIH flächengleich. Abbildung 3. Gnomonsatz Dies liegt daran, dass die Diagonale AG das Rechteck in zwei Dreiecke derselben Fläche zerlegt. Weil die Dreiecke 1 und 2, sowie 3 und 4 ebenfalls dieselbe Fläche haben, müssen die beiden gefärbten Rechtecke ebenfalls dieselbe Fläche haben. Es gilt daher bd = ac, was b : c = a : d ergibt. Dies ist der Strahlensatz für die beiden ähnlichen Dreiecke ABC und CFG. 2. Das Schubfachprinzip Das Schubfachprinzip besagt, dass man 21 Perlen nicht in 20 Schubfächer legen kann, ohne dass in einem Schubfach nicht mindestens 2 Perlen liegen. Aufgabe 1. Zeige, dass unter 13 Personen mindestens zwei im gleichen Monat Geburtstag haben. Die Schubfächer sind die 12 Monate, die Perlen die 13 Personen. Weil es mehr Perlen als Schubfächer gibt, liegen in einem Schubfach mindestens zwei Perlen. Aufgabe 2. In einem Raum sind 100 Personen. Zeige, dass es zwei Personen A und B gibt, welche dieselbe Anzahl von Leuten kennnen. 4 ABGABE AM MITTWOCH, 11.10.2017 Hierbei ist angenommen, dass kennen“ auf Gegenseitigkeit beruht, dass also zwei ” Personen sich entweder gegenseitig kennen oder sich nicht kennen. Wenn eine Person n Bekannte hat, kommt es in die Schublade mit der Nummer n; dabei gibt es Schubladen mit den Nummern von 0 bis 99. Wenn es 101 Personen wären, wäre alles klar. Allerdings greift das Schubfachprinzip auch hier: die Schubfächer 0 und 99 können nicht gleichzeitig belegt sein, weil es sonst jemanden gäbe, der niemand kennt, und jemand, der alle kennt. Also sind 100 Personen auf 99 Schubfächer verteilt, und es gibt eine Schublade mit zwei Personen. Aufgabe 3. Unter 9 natürlichen Zahlen gibt es immer zwei, deren Differenz durch 8 teilbar ist. Die Schubfächer sind die Reste, welche die Zahlen bei Division durch 8 lassen. Mindestens zwei haben denselben Rest, und deren Differenz ist durch 8 teilbar. Aufgabe 4. Fünf Fliegen sitzen in einem gleichseitigen Dreieck mit Seitenlänge 2. Zeige, dass es zwei Fliegen gibt, die höchstens Abstand 1 voneinander haben. Hier zerlegen wir das gleichseitige Dreiecke mithilfe der Seitenmittelpunkte in vier kleinere gleichseitige Dreiecke der Seitenlänge 1. Nach dem Schubfachprinzip sitzen in einem Dreieck mindestens zwei Fliegen. Diese haben notwendig Abstand ≤ 1. Aufgabe 5. Aus den Zahlen 1, 2, 3, . . . , 32 werden 17 Zahlen ausgewählt. Zeige, dass darunter immer zwei sind, deren Summe 33 beträgt. Wir legen die Zahlen in 16 Schubfächer; die Zahlen n ≤ 16 kommen in das Schubfach Nummer n, die Zahlen n ≥ 17 in das Schubfach 33 − n. In einem Schubfach liegen mindestens zwei Zahlen, nämlich n und 33 − n. Ihre Summe ist offenbar 33. Aufgabe 6. Unter fünf Punkten in der Ebene mit ganzzahligen Koordinaten gibt es zwei, deren Mittelpunkt ebenfalls ganzzahlige Koordinaten hat. Wieviele Punkte braucht man mindestens, damit das entsprechende Problem in drei Dimensionen stimmt? Aufgabe 7. In einem Quadrat der Seitenlänge 30 liegen 7 Punkte. Zeige, dass zwei davon Abstand ≤ 20 haben. Genügen 6 Punkte ebenfalls?











