Karl-Heinz Pfeffer Analysis für Fachoberschulen

Karl-Heinz Pfeffer
Analysis
für Fachoberschulen
Karl-Heinz Pfeffer
Analysis
für Fachoberschulen
Ein Lehr- und Arbeitsbuch zur modernen Mathematik
Mit 220 Abbildungen
und mehr als 2000 Aufgaben
5., durchgesehene Auflage
IJ
vleweg
Die Deutsche Bibliothek - CIP-Einheitsaufnahme
Ein Titeldatensatz fiir diese Publikation ist bei
Der Deutschen Bibliothek erhiiltlich.
1. Auflage 1981
2., durchgesehene Auflage 1985
3., verbesserte Auflage 1988
4., verbesserte und erweiterte Auflage 1998
5., durchgesehene Auflage 2000
Aile Rechte vorbehalten
© Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig,lWiesbaden, 2000
Der Verlag Vieweg ist ein Unternehmen der Fachverlagsgruppe BertelsmannSpringer.
Das Werk einschIieBlich aller seiner Teile ist urheberrechtIich geschiitzt. Jede
Verwertung auBerhalb der engen Grenzen des Urheberrechtsgesetzes ist
ohne Zustimmung des Verlags unzuliissig und strafbar. Das gilt insbesondere
fiir VervielfiiItigungen, Ubersetzungen, Mikroverfilmungen und die Einspeicherung und Verarbeitung in elektronischen Systemen.
www.vieweg.de
Konzeption und Layout des Umschlags: U1rike Weigel, www.CorporateDesignGroup.de
Technische Redaktion: Wolfgang Nieger, Wiesbaden
Satz: KnfhtIaciaren Svornost G.m.b.H., Bratislava
und Publishing Service Rolf-Erich Schulz, Dreieich
Gedruckt auf siiurefreiem Papier
ISBN 978-3-528-44006-0
ISBN 978-3-322-91907-6 (eBook)
DOI 10.1007/978-3-322-91907-6
v
Vorwort
Das vorliegende Unterrichtswerk zur Analysis ist ein Lehr- und Arbeitsbuch für Fachoberschulen der
Klassen 12.
Es berücksichtigt in besonderem Maße die unterschiedlichen mathematischen Vorkenntnisse der Fachoberschüler, indem wiederholende Inhalte angeboten werden, die je nach Bedarf mehr oder weniger
selbständig von Schülerinnen und Schülern erarbeitet werden können. Aus diesem Grunde kann das Buch
ebensogut bereits in den 11. Klassen eingeführt werden und bietet sich darüberhinaus für jene Absolventen der Erwachsenenbildung an (Volkshochschulen etc.), weIche die Fachhochschulreife erwerben
möchten.
Analysis for Fachoberschulen entstammt der langjährigen Unterrichtspraxis des Verfassers an einer
Fachoberschule Technik. Die entsprechende Orientierung am technischen und physikalischen Erfahrungs- bzw. Erlebnisbereich der Lernenden ist dabei so erfolgt, daß eine Verwendung in den anderen
Fachrichtungen (insbesondere Seefahrt und Agrarwirtschaft) ebenfalls gut möglich ist.
Wegen der spezifisch technischen Akzentuierung eröffnet sich auch ein Unterrichtseinsatz in einschlägigen
Berufsoberschulen sowie in Fachgymnasien Technik.
Der didaktische Leitgedanke dieses Buches beinhaltet, grundlegende Kenntnisse über Funktionen zu
vermitteln, ohne dabei die Theorie überzubewerten. Dazu gehört es, hinführend zu den klassischen
Methoden der Analysis auch die hierfür wesentlichen elementaren Rechentechniken und geometrischen
Denkweisen bereitzustellen und einzuüben.
Das geschieht zunächst einmal durch bewußt breit angelegte Überlegungen zu den linearen und quadratischen Funktionen, an die sich die einschlägigen Nullstellenermittlungen ganzrationaler Funktionen
höheren Grades anschließen. Abgerundet wird die elementare Funktionenlehre durch wiederholende
Betrachtung der trigonometrischen Grundfunktionen und mündet ein in die Erarbeitung der allgemeinen
Sinusfunktion.
Dieser Einstieg in die Analysis, je nach Lerngruppe und Lernintention abkürzbar, hat den Vorteil, daß
nach der sich anschließenden Erarbeitung des Grenzwertbegriffes über Folgen bzw. über Funktionen den
Lernenden die Problemstellungen der Differential- und später auch der Integralrechnung durchsichtiger
erscheinen: Grundsätzliche Vorgehensweisen werden wieder aufgegriffen (Wiederholungseffekt!) und
gemäß Spiralprinzips in erweitertem Zusammenhang angewandt.
Besonders erwähnenswert ist, daß die Integralrechnung anschaulich über Flächeninhaltsfunktionen
eingeführt wird.
Viele Beispielaufgaben mit Lösungen (~ ) erleichtern das selbständige Einüben des Stoffes. Das umfangreiche, zum großen Teil anwendungsbezogene Aufgabenmaterial ermöglicht handlungsorientierte Unterrichtsansätze, schülerorientierte Übungsphasen und intensive Vorbereitung auf Lernkontrollen. Die
Aufgabenanordnung ist innerhalb derselben Thematik, soweit möglich, im Sinne einer methodischen
Reihe schwierigkeitsgraddifferenziert erfolgt; besonders schwierige Aufgaben sind kursiv gekennzeichnet.
Die mit * versehenen Inhalte dienen der Abrundung. Sie können ohne Einfluß auf das weitere Vorgehen
auch weggelassen werden bzw. ermöglichen den Einsatz des Unterrichtswerkes über den vom Titel her
genannten Adressatenkreis hinaus.
Hannover, im Januar 1997
Karl-Heinz Pfeffer
VI
Inhaltsverzeichnis
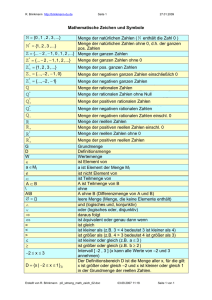
Mathematische Zeichen und Begriffe
x
Analysis
I Die reellen Zahlen
. . . . . . . . . . . . . . . .
1.1
Die Grundeigenschaften der reellen Zahlen
1.1.1 Von den natürlichen zu den reellen Zahlen.
Die natürlichen Zahlen
Ganze Zahlen . .
Rationale Zahlen .
Irrationale Zahlen
Reelle Zahlen . .
1.1.2 Lagebeziehungen reeller Zahlen
Intervall, Umgebung, absoluter Betrag
1.2 Das Rechnen in IR . . . . . . . . .
1.2.1 Der binomische Satz . . . . .
1.2.2 Gleichungen und Ungleichungen
Grundlagenwiederholung . . .
Lineare Ungleichungen . . . .
Quadratische Gleichungen und Ungleichungen
Exponentialgleichungen .
2 Funktionenlehre
2.1
Grundlagen
2.1.1 Paarmengen .
2.1.2 Funktionen .
Funktionen als Spezialfall von Relationen
Definitions- und Wertemenge
Schreibweise von Funktionen
2.2 Ausgewählte elementare Funktionen
2.2.1 Lineare Funktionen
Die Gerade als Graph linearer Funktionen
*Anwendung linearer Funktionen
Nullstellen linearer Funktionen . . . . .
Schnittpunkt zweier Geraden
.... .
Schnittwinkel zweier Geraden - Orthogonalität .
Erstellung linearer Funktionen
*Länge einer Strecke .
*Mitte einer Strecke . . . . .
2
2
2
2
3
4
7
9
14
17
18
23
23
27
31
37
41
41
41
44
44
45
45
50
50
50
56
59
60
63
67
73
74
VII
Inhal tsverzeichnis
2.2.2
Quadratische Funktionen . . . . . .
Die Normalparabel . . . . . . . . .
Allgemeine Form der Scheitel gleichung
Nullstellen quadratischer Funktionen
Schnittpunkte Gerade - Parabel . .
Schnittpunkte Parabel - Parabel . .
Erstellung quadratischer Funktionen
*2.2.3 Lineare und quadratische Betragsfunktionen
2.2.4 Umkehrfunktionen (Umkehrrelationen)
2.2.5 Ganzrationale Funktionen. . . . . .
Reine Potenzfunktionen . . . . . . .
Nullstellen ganzrationaler Funktionen.
Kurvenverlauf und Symmetrie . . . .
*Das Hornerschema . . . . . . . . .
2.3 Trigonometrische Funktionen (Kreisfunktionen)
2.3.1 Die Eigenschaften der trigonometrischen Grundfunktionen
Das Bogenmaß eines Winkels . . . .
Die Sinus- und Kosinusfunktion . . .
Die Tangens- und Kotangensfunktion .
2.3.2 Die allgemeine Sinusfunktion
3 Folgen und Reihen
3.1
. . . . .
Grundlagen . . . . . .
3.1.1 Folge als Funktion
3.1.2 Schreibweise von Folgen
3.1.3 Eigenschaften von Folgen
3.1.4 Reihen . . . . . . . .
3.2 Spezielle (endliche) Folgen. . .
3.2.1 Arithmetische Folgen und Reihen
Das Bildungsgesetz . . . . . . .
Arithmetische Folgen als lineare Funktionen.
Die Summenformel der arithmetischen Reihe
*Vollständige Induktion . . . . .
3.2.2 Geometrische Folgen und Reihen
Das Bildungsgesetz . . . . . . .
*Geometrische Folgen als Exponentialfunktionen
Die Summenformel der geometrischen Reihe .
*3.2.3 Zinseszinsrechnung . . . . . . . . . . . .
3.3 Grenzwert von Folgen . . . . . . . . . . . . .
3.3.1 Unendliche geometrische Folgen und Reihen.
*Periodische Dezimalzahlen als Grenzwert unendlicher
geometrischer Reihen . . . . . . . . . . . . . .
3.3.2 Verallgemeinerung des Grenzwertbegriffes . . . . .
Konvergenz ausgewählter nicht-geometrischer Folgen
Definition des Grenzwertes und 1. Konvergenzkriterium .
76
76
80
84
88
91
92
95
97
104
104
108
115
119
123
124
124
125
130
133
138
138
138
140
142
145
147
147
147
149
150
152
155
155
159
162
166
168
168
173
177
177
180
VIII
Inhaltsverzeichnis
3.3.3
Das Rechnen mit Grenzwerten.
Grenzwertsätze . . . . . . .
Grenzwert von Quotientenfolgen
*3.4 Wachstum und Zerfall . . . . . . .
3.4.l Euler'sche Zahl und e-Funktion
3.4.2 Spezielle Anwendungsformen der e-Funktion
4
Grenzwert von Funktionen - Stetigkeit . . . . . . . . .
4.1
Grenzwerte von Funktionen . . . . . . . . . . .
4.1.1 Erfordernis diverser Grenzwertbetrachtungen
4.1.2 Rechnerischer Umgang mit Grenzwerten
*4.1.3 Anwendung auf Kurvenuntersuchungen einfacher gebrochenrationaler Funktionen .
4.2 Stetigkeit . . . . . . . .
4.2.1 Begriff der Stetigkeit
4.2.2 Globale Stetigkeit
5
Differentialrechnung. . . . . . . . . . . .
5.1
Das Tangentenproblem . . . . . . . .
5.1.1 Die Differenzenquotientenfunktion
5.1.2 Allgemeine Definition des Differentialquotienten
5.1.3 Einfache Differentiationsregeln . . . . . . . .
Potenz-, Konstanten-, Summenregel
*5.1.4 Differenzierbarkeit und Stetigkeit .
*5.1.5 Anwendung in der Physik. . . . .
5.2 Anwendung auf Kurvenuntersuchungen . .
5.2.1 ExtremstelIen von Funktionen - Krümmungsverhalten
5.2.2 Wendepunkte . . . . . . . . . . . . . .
5.2.3 Kurvendiskussion ganzrationaler Funktionen
5.3 Extremwertaufgaben mit Nebenbedingungen
6
Integralrechnung
6.1
. . . . . . .
Das bestimmte Integral . .
6.1.1 Das Flächenproblem
Vorbemerkungen. .
Flächeninhaltsfunktion
Das bestimmte Integral als Operator
Das bestimmte Integral für f(x) < 0
6.1.2 Die Berechnung des bestimmten Integrals ganzrationaler
Funktionen . . .
Integrierbarkeit . . . . . . . . . . . . .
Integrationsregeln . . . . . . . . . . . .
Fläche zwischen Funktionsgraph und x-Achse
Fläche zwischen zwei Funktionsgraphen .
Rotationsvolumen . . . . . . . . . . . .
181
181
182
183
183
187
191
191
191
194
202
211
211
215
216
216
216
219
221
229
231
234
235
239
243
251
260
260
260
260
262
268
270
272
272
273
277
280
284
Inhal tsverzeichnis
*6.2 Die Integration als Umkehrung der Differentiation . . . . . . .
6.2.1 Das bestimmte Integral als Funktion seiner oberen Grenze
6.2.2 Stammfunktion und unbestimmtes Integral . . . . . . .
6.2.3 Die Berechnung bestimmter Integrale mit Hilfe von Stammfunktionen
*7 Vertiefung der Differentialrecbnung
7.1 Weitere Differentiationsregeln
7.1.1 Produktregel . .
7.1.2 Quotientenregel . . .
7.1.3 KeUenregel . . . . .
7.2 Kurvendiskussion gebrochen-rationaler Funktionen.
7.3 Kurvendiskussion trigonometrischer Funktionen . .
7.3.1 Die Differentiation der trigonometrischen Grundfunktionen
Die Ableitungen des Sinus und Kosinus . . . .
Die Ableitungen des Tangens und Kotangens .
7.3.2 Zusammengesetzte trigonometrische Funktionen
Sacbwortverzeicbnis . . . . . . . . . . . . . . . . . . .
IX
285
285
289
294
297
297
297
298
300
304
313
313
315
317
318
322
x
Mathematische Zeichen und Begriffe
1 Logik
dejinitionsgemäß gleich; Kennzeichnung einer
Definitionsgleichung, bei welcher der zu definierende Begriff auf der Seite des Doppelpunktes steht.
/\
und (im Sinne von sowohl ... als auch)
v
oder (im nicht-ausschließenden Sinn)
daraus folgt; wenn ... , dann
(p ~ q: Aus p folgt q, d. h. p ist hinreichende
Bedingung für q und q ist notwendige Bedingung für p.)
äquivalent (gleichwertig); genau dann ... , wenn
(p~q:
Aus p folgt q und umgekehrt)
2 Relationen zwischen Zahlen
a= b
a gleich b
a i= b
a ungleich b
a< b
a ::::; b
a kleiner b
a kleiner oder gleich b
a> b
a~b
a größer b
a größer oder gleich b
a ~ b
a ungefähr gleich b
a~b
a entspricht b (gebräuchlich z.B. bei Maßstabsangaben)
3 Mengen
A, B, C, ... , M, N, ...
Mengen
aEM(M3a)
afjcM
a ist Element von M (M enthält a)
{a, b,
C,
a ist nicht Element von M
Menge mit den Elementen a, b, c und d
d}
{xl··· }
Menge aller x, für die gilt ...
{xl···}M
{}
Menge aller
leere Menge
A=B
A gleich B, d.h. XEA~XEB
Ac B(B
=:J
A)
XE
M, für die gilt ...
A ist (echte) Teilmenge von B, d.h. XE A ~ XE B
und A i= B (B ist (echte) Obermenge von A)
A ist echte oder unechte Teilmenge von B
(d.h. Ac B oder A = B)
XI
Mathematische Zeichen und Begriffe
A$B
A (\ B:= {XIXEA /\ xEB}
A ist nicht Teilmenge von B
A geschnitten B; Schnittmenge (Durchschnitt)
von A und B
Au B:= {XIXEA v xEB}
B\A:= {XIXEB /\ x~A}
A~: = {xlx~ Aln für A s; B
A x B:={(x;y)lxEA /\YEB}
Avereinigt B; Vereinigungsmenge von A und B
Bohne A; Differenzmenge von Bund A
Ergänzungsmenge von A zu B, d.h. A u A~ = B
A kreuz B; Paarmenge von A und B (kartesisches Produkt)
charakteristische Mengen
IN:= {I, 2, 3, ... }
INo : = IN u {o}
7l:={ ... ,-I,O,I,2, ... }
Menge der ganzen Zahlen
~:= {~IPE71 /\ QE71\{O}}
Menge der rationalen Zahlen
IR
.D : = {xlx~~hR
IR+
Menge der natürlichen Zahlen
Menge der natürlichen Zahlen einschl.
Menge der reellen Zahlen
Menge der irrationalen Zahlen
Menge der positiven reellen Zahlen
IRri : = IR + u {O}
IR - : = IR\IRri
IR*:= IR\{O}
[a; b] : = {xla :( x :( b}IR
Menge der reellen Zahlen ohne
geschlossenes Intervall
Ja; b[:= {xla < x < b}IR
offenes Intervall
[a; b[:= {xla:( x < b}IR}
Ja; b] : = {xla < x :( b}IR
halboffene Intervalle
Ixl:=
Betrag einer (reellen) Zahl x
{+x
f~r xEIR~
-x fur XEIR
°
Menge der positiven reellen Zahlen einschl.
°
Menge der negativen reellen Zahlen
°
4 Funktionen
Zahlen- und Mengenzuordnungspfeil
Relation als Teilmenge eines kartesischen Produkts
R
f(auch g oder h)
f:x~f(x)
f(x)
Y =f(x)
{ D~W
f: x~f(x)
Funktion als Spezialfall einer Relation
Funktionsvorschrift
Funktionswert (Bild von x); aber auch Funktionsterm
Funktionsgleichung
Funktionfmit Definitionsmenge D und Wertmenge W
XII
Mathematische Zeichen und Begriffe
Umkehrfunktion (Umkehrrelation)
Graph vonf(Punktmenge) mit dem Punkt P(xfy)
f ' , f" , flll , ... , f(n)
fog (gof)
Identitätszeichen ("ist identisch gleich"); Z.B.
Parabel P == Y = X z
Folge mit den Gliedern (a), az, ... ,an, ... )
(Folge als Funktion mit D ~ IN)
1., 2., 3., ... , n-te Ableitungsfunktion von f
Verknüpfungszeichen für verkettete Funktionen (f nach g bzw. g nach f)
5 Weitere Zeichen
unendlich
00
Grenzwert einer Folge für n gegen
00
Grenzwert einer Funktion f für x gegen X o
!im fex)
x-xo
n
Summationssymbol : a)
+ az + ... + an _ ) + an
b
f f(x)dx
bestimmtes Integral der Funktionfüber [a; b]
a
f
unbestimmtes Integral der Funktion f
f(x)dx
F(x)
=
f
f(x)dx
Stammfunktionen von f mit r(x)
=
fex).
6 Wichtige Begriffe
Definition
Die Bedeutung eines verwendeten Namens oder
Zeichens wird erklärt bzw. festgelegt.
Axiom
Anerkannter, nicht beweisbarer Grundsatz, aus
dem sich Sätze ableiten lassen.
Satz
Unter Beachtung der Gesetze der Logik werden
aus bereits bekannten Aussagen Schlußfolgerungen (Behauptungen) gezogen, die es zu beweisen gilt. - Zur Beweisführung darf auf eine
entsprechende Definition zurückgegriffen werden.
Analysis
Eines der bedeutsamsten Gebiete der Mathematik ist die Analysis, unter der man ganz
allgemein die Lehre von den Funktionen versteht. Ihre charakteristischen Methoden - sie
haben inzwischen I) zu einer mannigfaltigen Anwendung in Wissenschaft und Technik
geführt - basieren auf den Begriffen
Zahl, Funktion, Grenzwert
und kommen besonders deutlich in der Differential- und Integralrechnung, dem wichtigsten Teil der Analysis, zur Geltung.
Zur Hinführung ist es zweckmäßig, zunächst auf die oben genannten Grundbegriffe
einzugehen. Die beiden ersten sind aus vorangegangener Beschäftigung mit der Mathematik mehr oder weniger gut bekannt und bedürfen nunmehr im Rahmen eines systematischeren Aufbaus der Ergänzung und Vertiefung.
I) d. h. etwa seit dem 18. Jahrhundert
2
1 Die reellen Zahlen
1.1
Die Grundeigenschaften der reellen Zahlen
1.1.1 Von den natürlichen zu den reellen Zahlen
Die natürlichen Zahlen
Sie sind Grundlage für den vorzunehmenden Zahlenaufbau und wie folgt definiert:
Menge der natürlichen Zahlen: 1 IN: = {l, 2, 3, ... } I·
Die wesentlichsten Merkmale l ) dieser Zahlenmenge:
l. 1 ist die kleinste natürliche Zahl.
2. Zu jeder natürlichen Zahl n existiert ein eindeutig bestimmter Nachfolger
n' = n + 1.
(Also: I': = 2 = 1 + 1; 2': = 3 = 2 + 1; 3': = 4 = 3 + 1; usw .. )
3. Es gibt keine letzte (= größte) natürliche Zahl.
(Zu einer vermeintlich letzten natürlichen Zahl ließe sich immer noch die 1 addieren,
usw .. )
Der in Bild 1.1 dargestellte Zahlenstrahl veranschaulicht die Grundsätze, wobei die
Pfeilrichtung das Größerwerden anzeigt.
"'--1
o
7
I
2
I
3
I
,
I
5
I
•
6 (111)
Bild 1.1
IN ist angeordnet
Gemeint ist, daß sich die Elemente von IN durch die Kleiner-Relation 2) ordnen lassen. So
gilt z.B. 2< 5 und 5< 7, was zu dem Schluß führt, daß auch 2 < 7 ist.
IN ist abgeschlossen
Diese Eigenschaft bezieht sich auf die Grundrechenarten" +" und,,·". Sie besagt, daß
sowohl die Summe als auch das Produkt zweier natürlicher Zahlen wieder eine natürliche
Zahl ist; die beiden Verknüpfungen führen nicht aus IN heraus.
Sonderfall: Die Zahl I
Sie ist erklärt als neutrales Element der Multiplikation, d.h. der Faktor 1 verhält sich
neutral, bewirkt keine Veränderung.
I) Ausführlicher und mathematisch streng hat diese Grundsätze erstmalig ein italienischer Mathe-
matiker namens Peano (1858-1932) festgehalten. Sie heißen ihm zu Ehren Peano-Axiome.
2) von relatio (lat.): Beziehung
K.-H. Pfeffer, Analysis für Fachoberschulen
© Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig/Wiesbaden 2000
1.1
Die Grundeigenschaften der reellen Zahlen
3
Einbeziehung der Zahl 0
Das neutrale Element der Addition, die Zahl 0, ist in IN nicht enthalten. Ihre sinnvolle
Hinzunahme - in Bild 1.1 bereits angedeutet - führt auf
1 INo: = IN u {O} I, also INo = {O,
1,2,3, ... },
auch Menge der nicht-negativen ganzen Zahlen genannt.
Meinungsstreit, die Zahl 0 betreffend
Im mathematischen Schrifttum ist auch zu lesen, daß die Zahl 0 (entgegen den Peano-Axiomen) als
Element der Menge IN angesehen wird. Zur KlarsteIlung nur soviel: Für die weitere Beschäftigung
mit der Mathematik ist es letztendlich unerheblich, ob die Zahl Oder Menge IN zugerechnet wird
oder aber nicht. - Es ist einzig Definitionssache !
Die Notwendigkeit von Zahlenbereichserweiterungen
Die erste Zahlenbereichserweiterung ist vollzogen, der Grundgedanke für nachfolgende
Zahlenbereichserweiterungen soll angedeutet werden:
Die Menge IN bietet rechnerisch wenig Möglichkeiten. Das Bestreben, Rechenoperationen (möglichst) ohne Einschränkung gelten zu lassen, erfordert erweiterte, algebraisch
leistungsfähigere Zahlenmengen .
Dabei gilt es, folgende, Zahlenbereichserweiterungen generell zugrunde liegende Prinzipien zu berücksichtigen:
1. Der neue Zahlenbereich läßt sich mit Hilfe bereits definierter Zahlen beschreiben.
2. Die in der usprünglichen Zahlenmenge formulierten Grundsätze gelten auch in der
erweiterten Zahlenmenge (Permanenzprinzip).
3. Für den erweiterten Zahlenbereich werden - soweit nötig - zusätzliche, widerspruchsfreie Axiome formuliert.
Dieser stufenweise Aufbau des Zahlensystems mit einer schrittweisen Einführung neuer
Axiome soll in diesem Rahmen nicht in mathematischer Strenge durchgeführt werden.
Ansätze hierzu mögen ausreichen, das Wesentliche nachzuempfinden.
Ganze Zahlen
Die Einführung der negativ-ganzen Zahlen, dargestellt durch
7l-:
= {xix = -n
1\
nEIN}
ermöglicht die Zahlenbereichserweiterung von IN bzw. INo zur
Menge der ganzen Zahlen: 1 7l: =71- uINo I, also 7l = {... ,-3, -2, -1,0, 1,2,3, ... }.
INo und 7l- sind ebenso Teilmengen von 7l wie
die Menge der positiv-ganzen Zahlen mit 7l+ = IN I ),
die Menge 7lt: = 7l+ u {O} (= INo),
I)
somit gilt
+ n = n (n E IN)
4
Die reellen Zahlen
die Menge 7lü : = 7l- u {O} und
die Menge 7l* : = 7l\ {O}.
~
z/~
Ensprechend gilt also auch
= 7l+ U 7l- u {O},
7l
Bild 1.2 7l:= 7l+ u71- u{O}
was durch nebenstehendes Venn-Diagramm (Bild 1.2) veranschaulicht wird.
7l ist angeordnet
Der bemerkenswerte Sachverhalt, daß in 7l zu jeder positiv-ganzen Zahl n eine negativganze Zahl -n existiert, und daß gilt
erschließt, daß auch 7l angeordnet ist.
1
I
I
1
1
1
1
-7 -6 -5 -4 -3 -2 -1
I
0
Bild 1.3
2
3
4
5
6
7 (Z)
Die charakteristische Darstellung auf der Zahlengeraden (Bild 1.3) trägt dem Rechnung.
Anders formuliert: Je weiter die Zahlen links von der 0 stehen, desto kleiner sind sie, je
weiter sie rechts davon angeordnet sind, desto größer werden sie. - Der eingetragene Pfeil
veranschaulicht das Größerwerden.
Rationale Zahlen
Die Einführung der ganzen Zahlen bewirkte eine gegenüber den natürlichen Zahlen
größere algebraische Leistungsfähigkeit. Diese reicht jedoch nicht aus, um für eine solch'
einfache Gleichung wie z.B. 2x = 3 eine Lösung angeben zu können. Erforderlich ist eine
nochmalige Zahlenbereichserweiterung, die die Bruchzahlen (Quotient, bestehend aus
Zähler und Nenner) einbezieht.
Die Menge der rationalen 2) Zahlen mit
CQ:=
{~IPE711\ qE71*}
trägt diesen Überlegungen Rechnung, wobei CQ die Menge 7l enthält.
+2 +4
-2
Beispiele: 2 = - = - = ... = - = ... ;
+ I +2
- I
+3
-3
-I
+1
- 3 = - = - = ....
Entsprechend den ganzen Zahlen lassen sich auch die rationalen Zahlen weiter unterteilen, und zwar in
die Menge der negativ-rationalen Zahlen, bezeichnet mit CQ-,
die Menge der positiv-rationalen Zahlen, bezeichnet mit CQ +,
I) ein Axiom
2) von ratio (Jat.): Vernunft, Verstand, aber auch Verhältnis
1.1
5
Die Grundeigenschaften der reellen Zahlen
die Menge ~o: = ~- v {O},
die Menge ~t: = ~+ v {O} sowie
die Menge ~*:= ~\{O}.
Folglich gilt auch ~:= ~+ v~- v {O}, was unterstreicht, daß auch die Zahl OE~ ist,
mit qE71* geschrieben werden.
kann sie doch in der Form Q
q
Konstruktion rationaler Zahlen
Daß ~ aus der Menge lN bzw. 7l hervorgeht, läßt sich veranschaulichen. Bild 1.4 zeigt
exemplarisch die Konstruktion l ) des Bildpunktes, der die rationale Zahl r = ~ markiert.
Anschaulich dürfte klar sein, daß auch ~ gemäß Permanenzprinzip angeordnet2) ist.
-1
Bild 1.4
Konstruktion der rationalen Zahl r = ~
~
3
ist dicht
auf der Zahlengeraden
Wichtig ist, zwei wesentliche Unterschiede im Vergleich zwischen
herauszustellen:
~
und 7l (bzw. lN)
1. Keine rationale Zahl weist einen (unmittelbaren) Vorgänger oder Nachfolger auf.
2. Zwischen zwei vorgegebenen rationalen Zahlen (a < b) existiert mindestens eine weitere rationale Zahl z.B.
a + b.
2
r = - - mlt a
< r < b.
Bild 1.5
o
a
r
I
b
..
(Q)
a<a
+ b < b (~ ist dicht!)
2
Bild 1.5 veranschaulicht den Sachverhalt für r E ~+.
Hieraus läßt sich ableiten, daß es zwischen zwei verschiedenen rationalen Zahlen stets
unendlich viele rationale Zahlen gibt:
Die Elemente von ~ liegen dicht 3).
I) Anwendung des 1. Strahlensatzes
2) Man beachte: -1 < -1/1000
3) Die Elemente von 'TL liegen nicht dicht; denn es existiert z.B. zwischen 1 und 2 nicht mindestens
eine weitere ganze Zahl.
6
Die reellen Zahlen
Der Kehrwert
Wegen der vorgenommenen Zahlenbereichserweiterung existiert nunmehr zu jeder Zahl
CQ* eine reziproke Zahl (= Kehrwert) !E CQ*
rE
mit der Eigenschaft
[!=-~T)
O.
r
Hinweis:
Für! wird auch r- I geschrieben.
r
Hier gilt besonders zu beachten - wie bei der Definition von CQ bereits angegeben-, daß
im Nenner eines Bruches niemals die Zahl 0 auftreten darf.
Exakt gesagt: CQ ist nullteilerfrei. 2)
Esseix= l=x 2 = l<:o>x 2 -1 =x-I
Faktorisieren des linken Terms: (x - I)(x + I) = x - I
Division mit (x - I):
x +I = I
Beispiel:
x
= o.
Somit wäre I = 0, oder ... ? Bitte selbst Fehlersuche vornehmen!
Dezimalbrüche als rationale Zahlen
Als Überleitung zu einer nochmals erforderlichen Zahlenbereichserweiterung soll der
Blick auf Dezimalbrüche gelenkt werden.
a) endliche Dezimalbrüche
Die dekadische Schreibweise kann nicht verunsichern: Endliche Dezimalbrüche lassen
sich exakt in Form eines Bruches schreiben und ggf. soweit kürzen, daß Zähler und
Nenner keinen gemeinsamen Teiler mehr haben.
1
25
1
125
1
. .
5
BeIspIele: 0,5 = - ="2; 0,25 = - = 4; 0,125 = - - = s·
10
100
1000
b) unendliche periodische Dezimalbrüche
°
Ein geradezu klassisches Beispiel ist die Dezimalzahl 0,333 ... , was kürzer durch die
Schreibweise 0,3 (gelesen: Komma Periode 3) angegeben wird.
Steht diese Zahl - exakt oder annähernd - für die rationale Zahl ~?
Sicher ist, daß sie sich gemäß Bild 1.6 einschachteln läßt durch endliche Dezimalbrüche:
o
0,3
l
< < 0,4
0,33 < ~ < 0,34
l
0,333 < < 0,334
usw.,
]
o
[
(RJ
1
"3
Bild 1.6 Einschachtelung der rationalen Zahl ~
I) noch ein Axiom
2) Dieses "Teile niemals durch 0" wird "roter Faden" bis hin zur Differentialrechnung sein.
1.1
Die Grundeigenschaften der reellen Zahlen
7
Das hilft hinsichtlich der Fragestellung nicht weiter. Vielleicht bringt die nachfolgende
Frage die Klärung:
Was ist richtig:
-
I
0,3 ="3
oder
Multiplikation mit Faktor 3 liefert
0,9 = 1
bzw.
0,9;:::; 1,
was Veranlassung sein mag, dem ungefahr gleich (;:::;) zuzuneigen.
Daß dem nicht so ist, zeigt nachfolgendes Rechenverfahren:
Aus r = 0,3 folgt 10r = 3,3;
eine Subtraktion läßt die Periode verschwinden:
IOr=3,3
r=0,319r
= 3 ~ r = "3,I d.h. "3I E CQ.
Fazit, ohne den schwierigen Beweis zu führen:
I
Jeder unendliche periodische Dezimalbruch ist eine rationale Zahl.
c) unendliche nicht-periodische Dezimalbrüche
Es sei vorweggenommen: Sie gehören nicht zu CQ.
Grund genug, eine neue Zahlenmenge einzuführen und den Zahlenbereich nochmals
zu erweitern.
Irrationale Zahlen
Die vorangegangenen Ausführungen haben gezeigt, daß die rationalen Zahlen dicht auf
der Zahlengeraden angeordnet werden können. Darf hieraus abgeleitet werden, daß sie
die Zahlengerade auch vollständig ausfüllen?
Die algebraische Gleichung x 2 = 2 soll herhalten, die Problematik aufzuzeigen.
Daß Ji (bzw. - Ji) Lösungen dieser Gleichung sind, kann aus früherer Beschäftigun,s.
mit der Mathematik als bekannt vorausgesetzt werden. Daß der vom ET-Rechner für.,)2
ausgewiesene endliche (!) Dezimalbruch nur eine Näherung darstellt, ist sicherlich auch
noch gegenwärtig. Inwieweit dieser aller Voraussicht nach unendliche Dezimalbruch
irgendwann einmal periodisch werden könnte und damit der Menge CQ zuzurechnen wäre,
ist im Rahmen der aufgezeigten Zahlenbereichserweiterungen bislang noch ungeklärt.
Das Prinzip der Einschachtelung - wie für r = ~ angewandt - hilft vielleicht weiter:
1
1,4
1,41
1,414
1,4142
1,41421
usw ..
<Ji<2
< Ji< 1,5
< Ji< 1,42
< Ji < 1,415
< Ji < 1,4143
< Ji< 141422
8
I
Die reellen Zahlen
J2
Wie 0,3 läßt sich auch
mittels endlicher Dezimalbrüche beliebig genau einschachteln.
In Anlehnung an die Ausführungen über unendlich-periodische Dezimalbrüche drängt
letztendlich exakt in Form eines Bruches
sich daher die Vermutung auf, daß auch
eine rationale Zahl.
geschrieben werden kann. Demnach wäre
J2
J2
Dem ist jedoch nicht so! - Das zu zeigen, kann nur mittels indirekten Beweises I) geschehen.
Indirekter Beweis zu
J2 ~ CQ
Dazu nimmt man an, daß es für x 2 = 2 doch eine rationale Variable x als Lösung gäbe.
Schreiben läßt sich das in der Form
x 2 = l!. = 2, wobei PE7l u. qE7l*, ferner p und q teilerfremd 2) zueinander.
q
Dann gilt
p2
-=2
q2
=> p2
= 2q2,
woraus wegen des Faktors 2 folgt, daß p2 und damit p eine gerade Zahl
darstellt, also: p = 2r, rE7l*.
Eingesetzt:
(2r)2
=
2q 2
2r 2 = q2, somit wäre wegen des Faktors 2 auch q eine gerade Zahl.
Das aber steht im Widerspruch zu der Annahme, p und q seien teilerfremd zueinander.
Die eingangs aufgestellte Behauptung, x sei eine rationale Zahl, kann somit nicht richtig
sein. Man sagt, x ist irrational, d.h. nicht-rational.
I
Irrational nennt man demnach solche Zahlen, die sich nicht exakt in Form eines
Bruches p/q darstellen lassen.
Diese Überlegungen lassen sich übertragen auf irrationale Zahlen wie J"j,
allgemein J?) sowie auf die entsprechend negativen Wurzelwerte.
J5
und
Noch allgemeiner: Das Symbol J-;4) mit aElN\{I} steht genau dann für eine irrationale
E CQ; denn
= 3).
Zahl, wenn nicht a das Quadrat einer rationalen Zahl ist
(J9
J9
Weitere Beispiele für irrationale Zahlen
"Fa
a) Zahlen der Form
mit nElN\{I} und aECQ+, z.B.
(Gegenbeispiele: ifij,
usw.);
V3i
VS, VlO, Vii usw.
b) die Zahl1! ';:::, 3,14159 ... (andere Näherung: 1! ';:::, ~~~);
I) Das Prinzip besteht darin, das Gegenteil der zu beweisenden Behauptung als wahr anzusehen und
daraus einen Widerspruch abzuleiten.
2) Heißt, daß der Quotient p/q soweit wie möglich gekürzt worden ist.
J) Primzahlen PEIN \ {I} sind Zahlen, die genau zwei Teiler haben, nämlich sich selbst und die I.
4) Quadratwurzel von a genannt
1.1
9
Die Grundeigenschaften der reellen Zahlen
c) die Zahl e ~ 2,71828 ... (vgl. ggf. Abschnitt 3.4.1);
d) Logarithmen, Z.B.
Ig i), definiert als diejenige (positive) Hochzahl, für die gilt IO Ig2 = 2;
Ib 32), definiert als diejenige (positive) Hochzahl, für die gilt 2'b3 = 3;
In 43), definiert als diejenige (positive) Hochzahl, für die gilt e1n4 = 4;
(Gegenbeispiel: Ig 100
= 2~ 102 = 100, lb 8 = 3~23 = 8 u.a.);
e) trigonometrische Funktionswerte der Form sin r . 1r, cos r . 1r, tan r . 1r, cot r . 1r,
wobei rECQ;
Beispiele: sin ~ = ~.
J2, cos~ = ~. /3, tan f = /3, cot~ = ~. /3 u.a.;
(Gegenbeispiele: sin ~ = ~, cos 0 .
1r
= 1, tan ~ = 1, cot ~ = 0 u.a.).
Die irrationalen Zahlen bilden in ihrer Gesamtheit die Menge JJ.
Reelle Zahlen
Die Existenz irrationaler Zahlen läßt vermuten, daß die Zahlengerade von den rationalen
Zahlen nicht vollständig ausgefüllt wird.
Obwohl CQ dicht ist, bestehen offensichtlich Lücken. Die Veranschaulichung dieses Sachgeschehen.
verhaltes soll beispielhaft wiederum anhand von
J2
Konstruktion von
J2
J2
Der irrationalen Zahl
kann genau ein Punkt auf der Zahlengeraden zugeordnet
werden. Die Konstruktion (Bild 1.7) basiert auf dem Lehrsatz des Pythagoras4):
(J2f =
12 + 12•
o
Bild 1.7
Konstruktion der irrationalen Zahl
2 (IR)
J2
IR ist vollständig
Um die Zahlengerade lückenlos auszufüllen, ist es sinnvoll, rationale und irrationale
Zahlen zusammenzufassen zur
Menge der reellen Zahlen:
I)
2)
3)
4)
I IR: = CQ v.u I
Ig n: = loglO n (dekadische Logarithmen)
Ib n: = log2 n (binäre Logarithmen)
In n: = log" n (natürliche Logarithmen)
benannt nach Pythagoras (um 570 v. Chr. - 497/96 v. Chr.); griech. Philosoph